突发事件多灾害点环境下确定性应急资源调度模型研究

薛晓芳，李宁宁，王泽江，张怀强，王汉宸

（1.太原理工大学，山西 太原 030024；2.成都农商银行崇州支行微贷中心，四川 崇州 611230；3.长春轨道客车股份有限公司转向架制造中心，吉林 长春 130062）

1 引言

近年来，各种破坏性突发事件在全球各地不断发生，给人们的生命和财产安全带来威胁，严重影响社会公共秩序稳定，突发事件成为世界范围内关注的焦点。为减少突发事件造成的各种损失，制定及时合理的应急救援措施显得尤为关键。

应急救援中资源的有效调度和及时供给是对灾害地区实施应急救援的关键环节，如何制定科学合理的应急资源调度制度，实现资源有效供给，对应急救援工作意义重大。J.L.Wybo、Russell、Tufekei、Guilherme 和Colonel Ali Alsayed 等先后就突发事件的动态预警、供应链流程、资源存放选址及供应路径等问题展开系统研究，讨论了突发灾害事件应急管理的各个层面。国内学者则主要集中在有关应急预案的建立及制定应急法律法规等方面，研究的范围比较小，对突发事件应急救援相关问题的研究成果相对较少。本文针对突发灾害应急资源调度难这一问题，对应急资源调度模型进行研究，力图构建一套合理有效的突发事件应急资源调度模型，为最大程度地减轻和挽回突发灾害事件引起的人民财产损失提供可靠的理论依据。

通过对应急资源调度数据资料的收集整理，总结出应急资源调度发展现状和存在地问题，在实际处理突发事件时，存在信息不畅通、资源储备不足、缺少专业应急救援人员、物流不畅通和多资源情况下调度粗放等问题，使应急救援工作效率不高，应急资源利用率低，因此要对应急资源调度的整个过程进行全面控制，才能提高应急资源的利用率，从而最大限度地提高对受灾地区的救援效率。

2 多灾害点应急资源调度模型构建

2.1 问题描述

在应急资源调度过程中，可以根据灾害地区信息反馈情况，将应急资源调度分为确定性和不确定性应急资源调度。确定性应急资源调度指灾害点需要的资源数量和资源从出救点配送到灾害点的单位时间已知，其它信息如配送单位资源的成本和灾害点及出救点的数量全部已知。在有多个出救点参与救援的前提下，可分为四种常见应急资源调度情况，分别是多出救点、单资源、单灾害点的情况，多出救点、多资源、单灾害点的情况，多出救点、单资源、多灾害点的情况和多出救点、多资源、多灾害点的情况。这种多样不可确定的情况增大了突发灾害事件中应急资源的有效调度和及时供给的难度，成为构建合理调度秩序的难题。

若需要调度的应急资源有u(u≥1)种，用Ze(1 ≤e≤u)表示第e种资源。各应急资源总的存储量大于总的需求量，S1,S2,…,Sm为m个应急资源存储点（或称为出救点），D1,D2,…,Dn为n个受灾点（或称为灾害点）。现在考虑其中一种应急资源，已知出救点Si(i=1,2,…,m)的实际供应量为Si；灾害点Dj(j=1,2,…,n) 的需求量为dj，从出救点Si(i=1,2,…,m)到灾害点Dj(j=1,2,…,n)的应急物资为xij，单位成本为cij，单位配送时间为tij，现要求制定出最优的应急资源调度方案，求出每个出救点应提供多少应急物资到哪个或哪几个灾害点，当si=0 时，表示第i个出救点不参与出救，应急资源调度目标是在使各灾害点的应急需求得到满足的前提下，使应急成本最少或运送时间最短。

当有u(u＞1)种应急资源时，用Ze(1 ≤e≤u)表示第e种资源，根据每个灾害点对各种应急资源需求紧迫度不同，可以将u种应急资源从每个出救点到每个灾害点的运送分为k(k≥1)个阶段，令各应急资源的重要程度为θe，则u种资源的重要程度比为θ1:θ2:…:θu，则有当λe的取值都不相同时，从每个出救点到每个灾害点应急资源配送划分为n个阶段，若λe中有δ个值相同时，则n种物资从每个出救点到每个灾害点的运送有e-δ个阶段。取λ(k)=minλe，则资源Ze从每个出救点到每个灾害点配送第一阶段的资源数量为x(Ze)ij=λ(k)θe。进而，依据该出救点剩下资源种类和数量，重新确定λ(k)的值，确定第二阶段配送资源种类和数量。依照此法，直到该出救点完成配送任务为止。

2.2 确定性应急资源调度模型

2.2.1 确定性单目标应急资源调度模型

（1）以应急成本最少为目标的单目标模型。根据上面的问题描述，可知各供应点总的物资供应量能满足各灾害点的总需求量，建立模型如下：

模型中，式（1）是目标函数，表示应急物资调度过程的应急成本最小，式（2）到式（5）为约束条件。其中式（2）表示实际总供应量等于总需求量；式（3）表示分配到每个灾害点的物资数量等于其需求量；式（4）表示每个出救点分配到各个灾害点的应急物资数量之和等于该出救点的实际运送应急资源的数量；式（5）表示从出救点i分配到灾害点j的物资数量为非负数。

该模型为线性规划模型，可用LINGO软件求解。

（2）以配送时间最短为目标的单目标模型。根据上述问题描述，可知各供应点总的物资供应量能满足各灾害点的总需求量，建立模型如下：

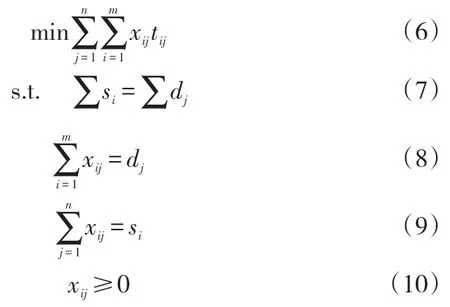
模型中，式（6）是目标函数，表示应急资源总配送时间最短，式（7）到式（10）是约束条件，其中式（7）表示实际总出救量等于总需求量；式（8）表示分配到每个灾害点的资源数量等于其需求量；式（9）表示每个出救点分配到各个灾害点的应急物资数量之和等于该出救点的实际配送应急资源数量；式（10）表示从出救点i分配到灾害点j的物资数量为非负数。

该模型同样为线性规划模型，可用LINGO软件求解。

2.2.2 确定性多目标应急资源调度模型

（1）确定性多目标应急资源调度模型。根据问题描述，以应急成本最少和配送时间最短为目标，建立模型如下：

模型中，式（11）和式（12）是目标函数，式（11）表示应急成本最少，式（12）表示配送时间最短；式（13）到式（16）表示约束条件。其中，式（13）表示各出救点实际总供应量等于各灾害点的总需求量；式（14）表示调度到每个灾害点的资源数量等于其需求量；式（15）表示从每个出救点调度到所有灾害点的资源数量等于其实际供应量；式（16）表示从出救点i调配到灾害点j的资源数量为非负数。

（2）确定性多目标应急资源调度模型的求解。针对上面建立的模型，采用基于二维欧氏距离客观赋权的模糊算法进行求解，f1(x)表示成本的函数，f2(x)表示时间的函数，因此有以成本最少和时间最短为目标的多目标函数：

第一步：确定f1(x)和f2(x)在X中的上、下界，即这两个函数分别在约束条件内的最大值和最小值。分别用sup{f1(x)} 、inf{f1(x)} 、sup{f2(x)} 和inf{f2(x)} 表示。

第二步：以μ1(x)和μ2(x)表示决策者对两个目标函数的满意度函数，对成本和时间型目标函数，其满意度函数定义为：

第四步：将多目标模型转化为单目标模型。

3 多灾害点应急资源调度模型实例分析

3.1 案例简介

某一地区发生地震，并且有四个受灾非常严重的地点，这里称为灾害点D1、D2、D3和D4。灾害点D1、D2、D3和D4所需的应急资源种类和数量见表1，这里用Z1代表水，Z2代表方便面，Z3代表帐篷，Z4代表棉衣。其附近区域有三个出救点S1、S2和S3，三个出救点储存的资源种类和数量见表2。四种资源按照Z1、Z2、Z3、Z4的顺序从各出救点到各灾害点的单位成本和时间分别见表3 和表4。由表1 和表2 可知，出救点储存的四种资源总量大于灾害点所需资源的总量。且四种资源的重要程度比为θ1:θ2:θ3:θ4=2:1:2:1。专家给出以成本和时间为目标函数的权重为ω1=0.2 和ω2=0.8。

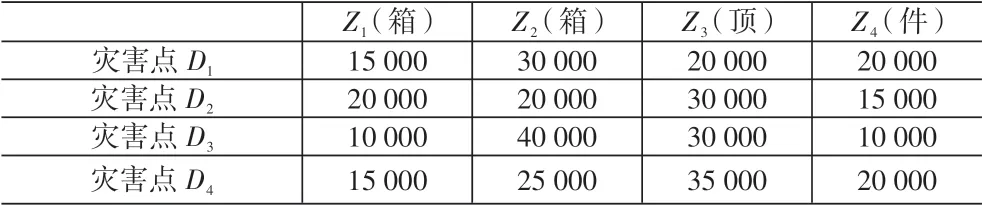
表1 各灾害点需要的资源种类和数量

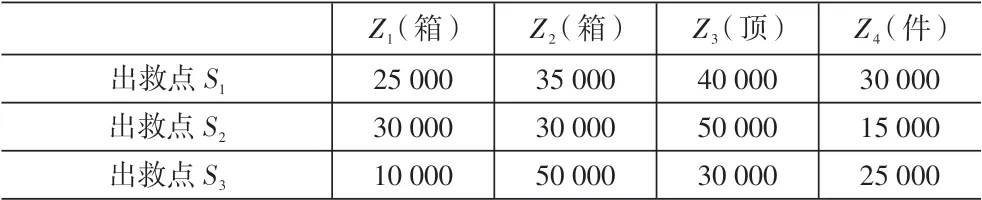
表2 各出救点储存的资源种类和数量

表3 四种资源从出救点到灾害点的单位成本

表4 四种资源从出救点到灾害点的配送时间

3.2 确定性应急资源调度模型的应用

3.2.1 确定性单目标应急资源调度模型的应用

（1）以应急成本最少为目标的单目标模型应用第一步：根据上述案例的数据，可建立资源Z1以应急成本最少为目标的数学模型：

同理，建立资源Z2、Z3、Z4以应急成本最小为目标的数学模型，用LINGO软件求得各种资源的需求量，并以应急成本最少为目标，得出资源调配方案如下：

出救点S1的调配任务：向D1配送5 000 顶帐篷和10 000件棉衣；向D2配送15 000箱方便面和15 000件棉衣；向D3配送10 000 箱水、20 000 箱方便面和5 000 件棉衣；向D4配送15 000箱水和35 000顶帐篷；

出救点S2的调配任务：向D1配送15 000 箱水、15 000 顶帐篷和10 000 件棉衣；向D2配送10 000 箱水和5 000 箱方便面；向D3配送30 000顶帐篷；向D4配送25 000箱方便面。

出救点S3的调配任务：向D1配送30 000箱方便面；向D2配送10 000箱水和30 000顶帐篷；向D3配送20 000箱方便面和5 000件棉衣；向D4配送20 000件棉衣。

根据四种资源的重要程度比不同，且θ1:θ2:θ3:θ4=2:1:2:1，针对从各出救点调配的资源种类和数量，由公式和x(Ze)ij=λ(k)θe计算得到各出救点到各灾害点各阶段配送结果如下：

出救点S1到灾害点D1的配送分为两个阶段，第一阶段配送5 000顶帐篷和2 500件棉衣；第二阶段配送7 500件棉衣。

出救点S1到灾害点D2的配送只有一个阶段，配送15 000箱方便面和15 000件棉衣。

出救点S1到灾害点D3的配送分为两个阶段，第一阶段配送10 000箱水、5 000箱方便面和5 000件棉衣；第二阶段配送15 000箱方便面。

出救点S1到灾害点D4的配送分为两个阶段，第一阶段配送15 000箱水和15 000顶帐篷；第二阶段配送20 000顶帐篷。

出救点S2到灾害点D1的配送分为两个阶段，第一阶段配送15 000 箱水、15 000 顶帐篷和7 500 件棉衣；第二阶段配送2 500件棉衣。

出救点S2到灾害点D2的配送只有一个阶段，配送10 000箱水和5 000箱方便面。

出救点S2到灾害点D3的配送只有一个阶段，配送30 000顶帐篷。

出救点S2到灾害点D4的配送只有一个阶段，配送25 000箱方便面。

出救点S3到灾害点D1的配送只有一个阶段，配送30 000箱方便面。

出救点S3到灾害点D2的配送分为两个阶段，第一阶段配送10 000 箱水和10 000 顶帐篷；第二阶段配送5 000 顶件帐篷。

出救点S3到灾害点D3的配送分为两个阶段，第一阶段配送5 000 箱方便面和5 000 件棉衣；第二阶段配送15 000 箱方便面。

出救点S3到灾害点D4的配送只有一个阶段，配送20 000件棉衣。

第二步：结果分析。灾害点D1需要的资源三个出救点都参与配送，但出救点S1负责配送帐篷和棉衣，出救点S2负责配送水、帐篷和棉衣，出救点S3只负责配送方便面，这说明方便面从出救点S3到灾害点D1配送需要的成本比其它资源从出救点S3到灾害点D1配送需要的成本少，故在满足灾害点需求资源的前提下，并从总应急成本的角度考虑，出救点S3只负责配送方便面到灾害点D1。

同理，向其它三个灾害点调度应急资源的过程与此相同。

（2）以配送时间最短为目标的单目标模型应用，可以将以成本最低为目标的模型应用作为参考，根据已建立的应急资源调度模型，计算资源调配方案。

3.2.2 确定性多目标应急资源调度模型的应用。根据已经建立的模型和案例数据，可建立资源Z1以应急成本最少和调配时间最短为目标的多目标模型：

应用LINGO 软件分别确定两个目标函数的上下界，计算目标函数满意度，结合专家给出的成本与时间的函数权重ω1=0.2、ω2=0.8，将多目标模型转化为单目标模型：

同理，可将资源Z2-Z4以应急成本最少和调配时间最短为目标的多目标模型转化为单目标模型，利用单目标模型的求解方法，计算得出以应急成本最少和配送时间最短为目标的资源调配方案：

出救点S1的调配任务：向D2配送20 000 箱水、20 000 顶帐篷和15 000件棉衣；向D3配送10 000箱方便面和20 000顶帐篷；向D4配送4 000 箱水和25 000 箱方便面和10 000 件棉衣。

出救点S2的调配任务：向D1配送15 000箱水和15 000件棉衣；向D3配送5 000 箱水、30 000 箱方便面和10 000 顶帐篷；向D4配送10 000箱水和35 000顶帐篷。

出救点S3的调配任务：向D1配送30 000 箱方便面、20 000 顶帐篷和5 000 件棉衣；向D2配送20 000 箱方便面和10 000 顶帐篷；向D3配送5 000 箱水和10 000 件棉衣；向D4配送10 000件棉衣。

根据四种资源的重要程度比不同，且θ1:θ2:θ3:θ4=2:1:2:1，针对从各出救点调配的资源种类和数量，由公式x(Ze)ij=λ(k)θe计算得到结果如下：

出救点S1到灾害点D1不参加配送。

出救点S1到灾害点D2的配送分为两个阶段，第一阶段配送20 000箱水、20 000顶帐篷和10 000件棉衣；第二阶段配送5 000件棉衣。

出救点S1到灾害点D3的配送只有一个阶段，负责配送10 000箱方便面和20 000顶帐篷。

出救点S1到灾害点D4的配送分为三个阶段，第一阶段配送4 000 箱水、2 000 箱方便面和2 000 件棉衣；第二阶段配送8 000 箱方便面和8 000 件棉衣；第三阶段配送15 000 箱方便面。

出救点S2到灾害点D1的配送分为两个阶段，第一阶段配送15 000箱水和7 500件棉衣；第二阶段配送7 500件棉衣。

出救点S2到灾害点D2不参加配送。

出救点S2到灾害点D3的配送分为三个阶段，第一阶段配送5 000 箱水、2 500 箱方便面和5 000 顶帐篷；第二阶段配送2 500 箱方便面和5 000 顶帐篷；第三阶段配送25 000 箱方便面。

出救点S2到灾害点D4的配送分为两个阶段，第一阶段配送10 000箱水和10 000顶帐篷；第二阶段配送7 500顶帐篷。

出救点S3到灾害点D1的配送分为三个阶段，第一阶段配送5 000箱方便面、10 000顶帐篷和5 000件棉衣；第二阶段配送5 000箱方便面和10 000顶帐篷；第三阶段配送20 000箱方便面。

出救点S3到灾害点D2的配送分为两个阶段，第一阶段配送5 000箱方便面和10 000顶帐篷；第二阶段配送15 000箱方便面。

出救点S3到灾害点D3的配送分为两个阶段，第一阶段配送5 000箱水和2 500件棉衣；第二阶段配送7 500件棉衣。

出救点S3到灾害点D4的配送只有一个阶段，负责配送10 000件棉衣。

对以上结果进行分析，灾害点D1需要的资源只有出救点S2和出救点S3参与配送，出救点S1不参与配送，出救点S2负责配送水和棉衣，出救点S3负责配送方便面、帐篷和棉衣，这说明在综合考虑成本和时间两个限制条件下，无论出救点S1向灾害点D1配送哪种资源，配送的代价都比其它两个出救点要大，所以对灾害点D1的应急救援，不选择从出救点S1配送资源。

同理，向其它三个灾害点调度应急资源的过程与此相同。

4 结论与展望

突发事件发生以后，最紧迫的工作就是应急救援，应急救援工作的核心在于根据突发事件发生后灾害地区信息的收集与反馈，制定合理的应急救援计划和实施应急资源调度。因此，本文为解决突发灾害环境下确定性应急救灾物资的合理高效调度这一问题，对现有的文献资料进行总结归类，针对不同情况及要求，建立多灾害点确定性应急资源调度模型，并结合案例进行求解应用，得出切实可行的突发灾害环境下确定性应急资源调度模型。因此，不难得出结论：

（1）应急资源调度问题是及时有效应对突发灾害条件下物资紧缺的关键性问题，涉及范围广，需求信息复杂，应对难度高，在构建并选用合理的应急资源模型时必须综合考虑并合理规划设计，本文根据应急资源调度的要求，构建多灾害点确定性应急资源调度模型，并利用案例进行模型验证，认为模型能够有效满足突发灾害条件下多灾害点确定性应急资源的调度。

（2）突发灾害条件下多灾害点应急资源调度体系是一个复杂的非线性系统，受到不同区域、不同地理条件、不同经济发展程度和交通水平的限制和约束，给应急资源调度问题的深入研究带来了困难。本文利用线性规划的思路，设置可能存在的诸多现实约束条件，结合相应的应急资源需求数据，刻画应急资源调度问题，并得到满意的验证效果。由此不难推断，多灾害点应急资源调度模型具有较强的应用可行性和合理性，在今后其他类似的突发灾害环境下具备广泛的普适意义和发展潜力。

[1]国家统计局.中国统计年鉴[M].北京:中国统计出版社,2013.

[2]中华人民共和国中央人民政府网[EB/OL].http://www.gov.cn/ziliao/flfg/2007-08/30/content_732593.htm,2007-08-30.

[3]严国灿.动态应急资源调度模型的研究及其应用[D].广州:中山大学,2010.

[4]Robert.An automated decision support system based on game theoretic optimization for emergency management in urban[J].Journal of Homeland Securit y and Emergency Management,2007,4(2):1.

[5]Ozdamaret A L.Emergency logistics planning in natural disasters[J].Annals of Operations Research,2004,129(3):217-245.

[6]Linet Ozdamar,Ediz Ekillei.Emengency logistics planning in natural disasters[J].Annals of Operations Researeh,2004,129(7):1-4.

[7]Patric J Owens,Anthony Forgione,Susan Briggs.Challenge of intemational disaster relief:use of a deployble rapid assembly shelter and surgical hospital[J].Disaster Management&Response,2005,(1):11-16.

[8]姚杰,池宏,计雷.带有潜变量的结构方程模型在突发事件应急管理中的应用[J].中国管理科学,2005,13(2):44-50.

[9]邬开俊,王铁君.带时限的多出救点应急物资调度模型及算法[J].计算机工程与应用,2012,48(30):19-23.

[10]高虹霓,赵一兵,李宁.基于多需求点的震灾应急物资调度模型研究[J].中国安全科学学报,2013,23(1):161-165.

[11]王胜,刘勇.考虑连续消耗的多出救点、多物资的应急调度问题的研究[J].三峡大学学报(自然科学版),2012,34(1):78-81.

[12]中国网.国家突发公共事件总体应急预案[EB/OL].http://www.china.com.cn/chinese/law/1086058.htm,2006-01-08.

[13]胡志华.多储备点多品种应急物资配送的多目标优化模型[J].数学的实践与认识,2013,(3):27-32.

[14]张怀强,王汉斌.突发灾害视角下多灾害点应急物资调配研究[J].物流技术,2013,(11):203-206.