基于浸入边界法的拍动翼尾涡结构与水动力分析
李宁宇, 苏玉民,刘葳兴,刘鹏,曹建
哈尔滨工程大学 水下机器人技术重点实验室,黑龙江 哈尔滨 150001
基于浸入边界法的拍动翼尾涡结构与水动力分析
李宁宇, 苏玉民,刘葳兴,刘鹏,曹建
哈尔滨工程大学 水下机器人技术重点实验室,黑龙江 哈尔滨 150001
摘要:针对目前拍动翼尾涡结构与水动力性能关系的研究有限,参数影响分析集中于水动力性能方面,且拍动翼等仿生流动的数值模拟经常涉及复杂移动边界问题的现状,应用自主开发的改进浸入边界法数值模拟拍动翼的非定常运动,探讨翼运动学、涡动力学和力的产生之间的关系。结果表明,所提出的边界条件重建算法兼顾计算效率和健壮性,开发的移动边界处理方法可有效解决浸入边界法中移动边界相关问题。三维拍动翼的尾涡由两列形状复杂的涡环组成,这两列涡环与尾流中心线成一定倾角向下游对流。水动力性能随运动参数的变化取决于力产生表象之下的涡动力学,包括涡的强度和方向、涡环的相互连接和粘性耗散。
关键词:拍动翼;浸入边界法;尾涡结构;水动力性能;推进机理;不可压缩N-S方程

苏玉民(1960-), 男,教授,博士生导师.
尽管水下机器人研究领域有很多给人印象深刻的创新,但是军方和科研团体都希望能够研究出更灵活机动的水下机器人获益,拍动翼推进器有望成为可行的技术方案之一。目前,国内外学者已对仿生拍动翼进行了大量研究。Mackowski等[1]实验测量了拍动翼的推力和效率,并分析运动参数对推进性能的影响。Politis等[2]采用边界元方法计算了较大参数空间范围内无粘流场中拍动翼的水动力性能,并在此基础上进行仿生翼推进器的设计。Wang等[3]利用FLUENT软件研究运动参数对拍动翼水动力性能的影响,并对推进机理进行简要探讨。文敏华等[4]基于动网格技术分析粘性力和压差力对拍动翼推力的贡献。但现有研究多侧重于水动力性能方面,对粘性流场中三维拍动翼的尾涡结构特征及演化机理的探讨还相对较少且不够深入,而水动力性能随运动参数的变化正是由相应的尾涡结构差异造成的。因此,系统分析运动参数对拍动翼尾涡结构的影响,研究尾涡结构与水动力性能的关系具有重要意义,而现阶段这方面的研究还是有限的。另一方面,拍动翼等仿生流动的数值模拟经常涉及复杂移动边界问题,而这类问题的高效求解一直是计算流体力学的难点。浸入边界法[5]为外形复杂结构在粘性流场中运动的数值模拟提供了新的途径,它利用拉格朗日方法跟踪物体运动边界,而流场控制方程在固定的笛卡尔网格上求解,不必按照物体形状生成复杂的贴体网格,对于移动边界问题也不需要流场的动网格更新。文中基于自主开发的改进浸入边界法数值求解非定常不可压缩N-S方程,研究拍动翼的尾涡结构和推进机理,并分析运动参数对水动力性能的影响,探讨翼运动学、涡动力学和力的产生之间的关系,理解水动力性能随参数变化的内在机制。
1拍动翼的计算模型
文中研究拍动翼的升沉俯仰耦合运动,拍动翼采用NACA0030翼型剖面,弦长为C,展长为S,置于均匀来流U中,如图1所示。

图1 拍动翼的计算模型
拍动翼在Y方向的升沉运动可以表示为
h(t)=h0cos(2πft)
式中:f为运动频率,t为时间,h0为升沉幅度。俯仰运动是绕距离前缘点1/4弦长位置处的展向轴(Z方向),可以表示为
式中:θ0为俯仰幅度,ψ为俯仰运动与升沉运动间的相位差,这里取为π/2,根据文献[6]的研究,此时拍动翼具有最佳的推进性能。
在拍动翼推进中一个关键的参数是斯特劳哈尔数[7],定义为
St=2h0f/U
雷诺数Re和翼的展弦比AR分别定义为
Re=UC/n
式中:ν为运动粘性系数。
AR=S/C
拍动翼的推力系数为
Cx=Fx/0.5ρU2A
式中: Fx为推力,ρ为流体密度,A为翼的投影面积。一个运动周期内平均推力系数可由下式计算:
式中:T为运动周期。拍动翼的推进效率可表示为

式中:Fy为升力,Mz为俯仰力矩。
2数值方法
2.1控制方程及其离散
流动控制方程为三维非定常、不可压缩N-S方程:

控制方程在固定的笛卡尔网格上离散,采用有限体积法求解,其中u表示单元中心的速度,p为压力,ρ和μ分别表示流体的密度与动力粘度,CV与CS分别表示控制体体积与控制体表面,n表示控制体表面的单位法向量。文中流场数值计算基于分裂步方法[8](fractional-step method)。在时间推进方案和空间离散格式上分别采用二阶隐式Crank-Nicolson格式和二阶中心差分[8]。
2.2浸入边界的处理
文中用ghost-cell方法[5]施加浸入边界对流动的影响,物体表面用适应性较强的三角形网格划分。
2.2.1网格单元属性的判断
首先利用射线法[9]进行网格单元内外状态的判断,然后可将网格单元分为以下3类(见图2):1)流体单元,即单元中心位于物体边界之外的单元;2)ghost-cell,即位于物体边界之内且至少有一个相邻单元位于流体内的单元;3)固体单元,即单元中心位于物体边界之内除ghost-cell外的其余单元。
2.2.2ghost-cell公式
下面利用局部流动插值建立ghost-cell上应满足的方程,以保证物面边界条件的正确实施。在之前的浸入边界法研究中,尽管各种边界条件重建算法已经被提出,然而对于这些方法的有效性和健壮性还没有给予足够关注。这里提出一个简单、快速的重建方案,而且该算法非常健壮,足以应对各种情况。
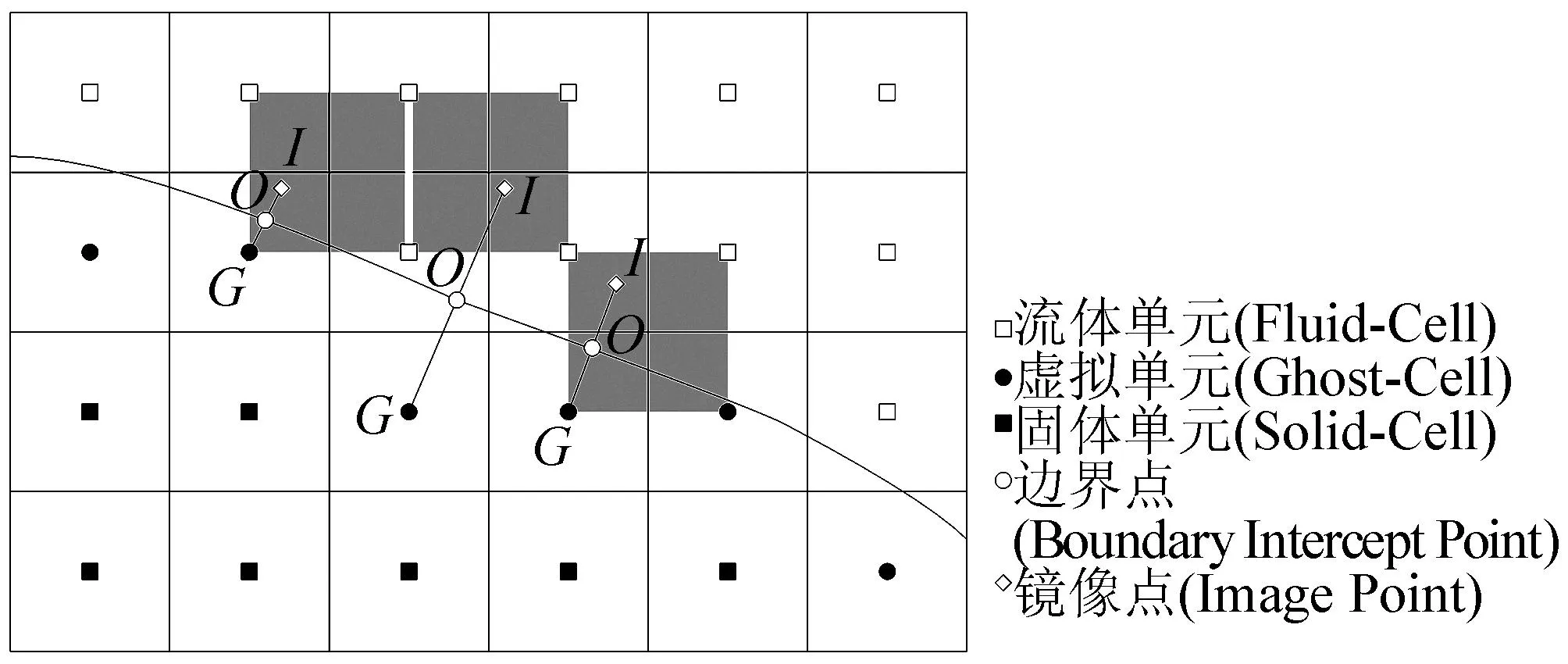
图2 ghost-cell浸入边界法示意
先从ghost-cell(G)向物面引垂线,如图2所示,将垂线与物面的交点O记为边界点,再将G与O的连线向流体内部延伸,得到G关于浸入边界在流体域内的镜像点I。在I点周围局部区域的流动变量φ可由如下的插值多项式表示:
φ=c1+c2x+c3y+c4z
式中:cj为多项式的系数,可用围绕I点的立方体的8个点中的3个流体点,再加上边界点O,如图2所示,总共4个点作为插值数据来计算,即
其中
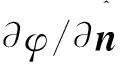
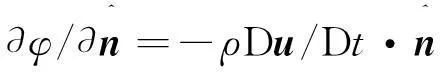
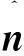
其中
多项式的系数一旦确定,在镜像点处的φ值即可由下式给出:
(1)
式中:βj是由插值多项式确定的权系数。对于速度的Dirichlet边界条件,根据中点公式有
(2)
将式(1)代入式(2),可得:
(3)
对压力的Neumann边界条件,利用二阶中心差分有
(4)
式中:Δl是法向线段的长度。将式(1)代入式(4),可得:
(5)
最后ghost-cell上的流动插值方程(3)和(5)与流体单元上的N-S方程联立求解。在以上过程中,可能会遇到2种特殊情况。一是围绕I点的8个点中有1个点是ghost-cell自身(如图2左侧那个ghost-cell所示),这不会引起任何额外的问题,因为其他7个点中的3个流体点和边界点O可作为插值点。二是围绕I点的8个点中包含其他的ghost-cell(如图2右侧那个ghost-cell所示),在这种情况下,如果围绕I点的8个点中的流体点的数量N≥3,那么这N个流体点中的3个连同边界点O可作为插值数据;若流体点的数量N<3,则插值模板由N个流体点、边界点O和3-N个其他的ghost-cell构成,尽管这确实暗示着一些ghost-cell上的φ值会彼此耦合,但并不会导致任何相容性问题,因为该ghost-cell上的流动插值方程与流体单元上的N-S方程连同其他ghost-cell上的方程是联立在一起求解的。根据以上分析,文中所提出的边界条件重建算法足够健壮,可以处理各种情况。
2.2.3移动边界
在浸入边界法中,流场控制方程在固定的笛卡尔网格上求解,因此在每一时间步的计算完成后,广阔的外流场并不需要像贴体动网格方法那样从旧网格到新网格的插值,但有些上一时间步的固体内部单元会由于边界的移动而成为流体单元,这些新出现的流体单元称之为fresh-cell[10],如图3所示,由于它们没有在流体中的有效时间历史,因此将给时间推进求解造成困难。
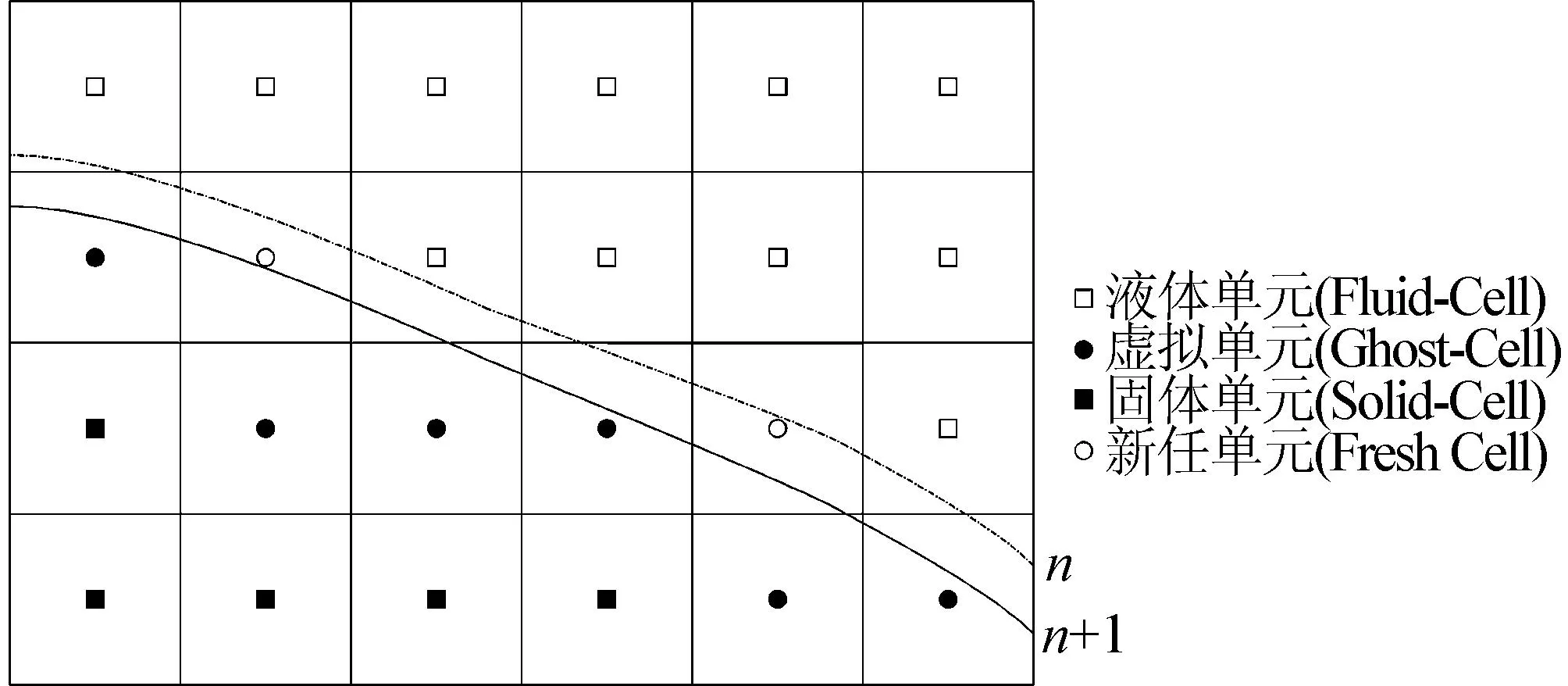
图3 边界移动形成Fresh-Cell示意
当前浸入边界法多采用显式时间推进格式,或对流项显式-扩散项隐式时间推进格式,为保证稳定性,要受到CFL条件的限制,因此一个时间步内边界的移动不会超过一层网格深度,Mittal等[10]对于fresh-cell不求解N-S方程,而是采用类似于ghost-cell的局部流动插值来得到其流动变量,Yang等[11]则提出了field-extension方法。在文中隐式时间推进格式框架下,可选取较大的时间步以提高计算效率,而不必担心稳定性问题,另外考虑到物体可能作大幅度运动,这些情况可能会使一个时间步内边界的移动超过一层网格深度,因此需开发适用于较大步长隐式时间推进和物体作大幅度运动的fresh-cell数值计算方法。这里采用改进Shepard插值[12]构造解决Fresh-cell的数值方案,该插值方法独立于网格拓扑结构,因而具有较强的适应性。具体做法是:1)每一时间步的计算完成后,将所有的边界点和ghost-cell作为插值数据,构成改进Shepard插值所需的散点插值集合;2)由改进Shepard插值得到所有固体单元上的流动变量。这样在接下来的时间推进求解中,所需的fresh-cell上的流动变量及空间导数都得以解决。
3结果与讨论
3.1数值方法的验证
为验证数值方法的正确性,将利用浸入边界法程序计算得到的平均推力系数与Read[6]的实验结果及采用面元法得到的计算结果进行比较,如图4所示,关于面元法的详细介绍可参考李宁宇等[13-14]之前的研究工作。
计算中拍动翼的参数为AR=3,Re=1 000,St=0.2-0.5,h0=0.5C,θ0=5°。可以看出,浸入边界法和面元法得出的Cxm变化趋势与实验结果一致,Cxm随St的增加而增大。由于考虑了流体粘性,相比于面元法,浸入边界法可以更精确地计算拍动翼在真实流动环境中的水动力。

图4 平均推力系数计算结果与实验数据对比
3.2尾涡结构
本节研究拍动翼的尾涡结构特征及演化机理,数值模拟中三维空间涡结构的识别采用Q判据[15],Q为速度梯度张量的第二不变量,在Q>0的区域内流体的旋转比较应变而言起主导作用。当AR=1.5,Re=200,St=0.5,h0=0.5C,θ0=30°时,拍动翼尾涡的透视图、侧视图和俯视图分别如图5(a)~(c)所示,图中根据计算出的涡矢量用箭头标出了涡的方向。结果表明尾涡由2列形状复杂的涡环组成,这2列涡环与尾流中心线成一定倾角向下游对流,这是三维拍动翼尾涡结构的重要特征。在图中标出了处于上面一列涡环之中的环R1与位于下面一列涡环之中的环R2。可以发现,在向下游对流的过程中,尾涡在Z方向稍有变窄,在Y方向逐渐变宽,此现象的机理可通过研究图5(a)~(c)中虚线所标出的区域内流向平面上的流动加以解释。图5(d)为在此平面内梢涡(TV1与TV2)和展向涡(TV2)的示意图,其中用实心圆表示的梢涡垂直纸面向外,用空心圆表示的梢涡垂直纸面向里,其他3个梢涡在1个梢涡上的诱导速度方向用箭头标出。
从诱导速度方向可以看出,同处上面涡环中的2个梢涡TV1彼此互相靠近,同处下面涡环中的2个梢涡TV2也是如此,从而导致尾涡在Z方向稍有变窄;处于不同涡环中的梢涡TV1和TV2趋于在垂向远离,从而造成尾涡在Y方向逐渐变宽。梢涡诱导的涡V1向上运动是导致涡环倾斜的主要机理,而一旦涡环倾斜,它的自诱导速度趋于使涡环沿着它的轴线向下游对流,这是2列涡环与尾流中心线成一定倾角的原因。由于涡环相对于来流方向是倾斜的,因此涡环沿其轴向所诱导的流动有一个流向成分和一个垂向成分,射流的流向成分与拍动翼的推力产生直接相关。

图5 尾涡结构与诱导机理
3.3St对尾涡结构和水动力性能的影响
本节进行斯特劳哈尔数的影响分析。数值模拟中St的变化范围是0.35~1.1,其他参数为AR=1.5,Re=200,h0=0.5C,θ0=30°。图6给出了St=0.35和St=0.95时拍动翼的尾涡结构,可结合图5中St=0.5时的情况来分析St对尾涡结构的影响。可以发现,当St=0.35时,一个明显的特征是St=0.5时所看到的梢涡之间的某些连接消失了,该现象是由于在低St下所形成的梢涡有更低的强度,这减弱了3.2节所阐述的梢涡之间相互诱导的机理。当St增加至0.5时,由拍动翼左右两侧产生的梢涡向中间靠近,相互融合, 形成涡环,并且可以看到连接2个涡列的发卡涡出现。随着St进一步增加到0.95,涡环倾角的改变使涡环的轴向与流向更加接近,并且2列涡环之间发展出更复杂的相互连接,显然随着St的增加,梢涡的强度增大,梢涡之间更强的相互诱导作用导致尾流在垂向变得更宽。

图6 尾涡结构随St的变化
平均推力系数和推进效率随St的变化如图7所示,可以看到推力随St的增加而增大,这是因为随St的增加,梢涡的强度增大,并且涡环倾角的改变使涡环的轴向与流向更加接近,从而射流的流向动量增加,根据动量定理,拍动翼产生的推力也相应增大。而推进效率先是随St的增加而增大,这显然是由推力的增大造成的,在St=0.8左右,效率达到峰值,约为19%,之后又逐渐减小,这是因为随St的增加,两列涡环之间产生更多的相互连接,下游的尾涡结构变得更加复杂,导致相反符号涡量之间的粘性抵消作用加强。注意文中采用基于浸入边界法的直接数值模拟探讨低雷诺数、低展弦比拍动翼的尾涡结构和水动力性能,故推进效率低于李宁宇等[13-14]之前有关高雷诺数、高展弦比拍动翼[15]的研究工作;根据Dong等[16]对低雷诺数、有限展弦比椭圆翼的研究,当AR=1.27和AR=2.55时得到椭圆翼的峰值效率分别约为18%和21%。

图7 水动力性能随斯特劳哈尔数的变化
3.4θ0对尾涡结构和水动力性能的影响
本节研究俯仰幅度的影响。计算参数为AR=1.5,Re=200,St=0.5,h0=0.5C,θ0=10°~40°。图8给出了θ0=10°和θ0=40°时拍动翼的尾涡结构,可结合图5中θ0=30°时的情况来研究θ0对尾涡结构的影响。可以看出,随θ0的增加,涡环倾角的改变使涡环的轴向与流向更加接近,这使得射流的流向动量增加;另一方面,涡环耗散速度加快,以致θ0=40°时远下游的涡环已经由于粘性耗散作用而消失。

图8 尾涡结构随俯仰幅度的变化
图9为平均推力系数和推进效率随θ0的变化,可以发现,推力先是随θ0的增加而增大,这是由于射流的流向动量增加,在θ0=20°附近推力达到最大值,而后因为尾流中涡环的耗散速度增加,推力又开始减小。与推力的变化情况类似,推进效率先是随θ0的增加而上升,这显然是因为推力的增大,当θ0为20°~30°某一值时,效率取得最大值,之后因推力减小和涡环耗散加快,效率又逐渐下降。
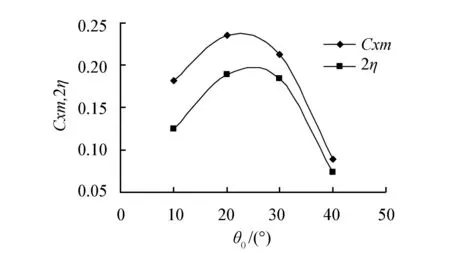
图9 水动力性能随俯仰幅度的变化
4结论
文中应用自主开发的改进浸入边界法数值模拟拍动翼的运动,分析其尾涡结构特征和演化机理,并探讨运动参数对尾涡结构和水动力性能的影响,得到如下结论:
1) 所提出的边界条件重建算法兼顾计算效率和健壮性,可保证物面边界条件的正确实施。
2) 基于改进Shepard插值构造的移动边界处理方法可有效解决浸入边界法中与移动边界有关的fresh-cell问题,并且该处理方法在选取较大时间步或物体作大幅度运动时也完全适用。
3) 实验结果和其他计算结果的比较表明,所开发的改进浸入边界法程序可很好地完成三维拍动翼在粘性流场中非定常运动的数值模拟。
4) 三维拍动翼的尾涡由2列形状复杂的涡环组成,这2列涡环与尾流中心线成一定倾角向下游对流,且尾涡在展向稍有变窄,在垂向逐渐变宽。在涡环轴向诱导速度作用下,翼的下游形成2股倾斜射流,射流的流向动量与推力的产生直接相关。
5) 随St增加,梢涡强度增加,2列涡环之间产生更多的相互连接,且涡环倾角的改变使涡环的轴向与流向更加接近,尾流在垂向变宽。推力随St增加而增大,存在一个最优St使推进效率最高。
6) 随θ0的增加,涡环倾角的改变使涡环的轴向与流向更加接近,且涡环耗散速度加快。推力和推进效率均随θ0的增加而先增大后减小,存在一个最优θ0使推进性能最佳。
参考文献:
[1]MACKOWSKIAW,WILLIAMSONCHK.Directmeasurementofthrustandefficiencyofanairfoilundergoingpurepitching[J].JournalofFluidMechanics, 2015(765): 524-547.
[2]POLITISGK,TSARSITALIDISVT.Flappingwingpropulsordesign:anapproachbasedonsystematic3D-BEMsimulations[J].OceanEngineering, 2014, 84(7): 98-123.
[3]SuYM,WangZL,ZhangX,etal.Numericalsimulationforhydrodynamicnumericalcharacteristicsofabionicflappinghydrofoil[J].ChinaOceanEngineering, 2012, 26(2): 291-304.
[4]文敏华,胡文蓉,刘洪.翼沉浮运动推力来源的数值研究[J].水动力学研究与进展,2012, 27(2):154-161.
[5]MITTALR,IACCARINOG.Immersedboundarymethods[J]AnnualReviewofFluidMechanicS, 2005(37): 239-261.
[6]READMB.Performanceofbiologicallyinspiredflappingfoils[D].Cambridge:MassachusettsInstituteofTechnology, 2006:133-135.
[7]PAN Y L, DONG X X, ZHU Q, et al. Boundary-element method for the prediction of performance of flapping foils with leading-edge separation[J]. Journal of Fluid Mechanics, 2012(698) : 446-467.
[8]FERZIGER J H,PERIC M. Computational methods for fluid dynamics[M]. New York: Springer-Verlag, 2002: 56-67.
[9]BORAZJANI I. Numerical simulations of fluid-structure interaction problems in biological flows[D]. Minneapolis, The Faculty of the Graduate School of the University of Minnesota,2008:1-273.
[10]MITTAL R, DONG H, BOZKURTTAS M, et al. A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries[J]. Journal of Computational Physics, 2008, 227(10): 4825-4852.
[11]YANG J M, BALARAS E. An embedded-boundary formulation for large-eddy simulation of turbulent flows interacting with moving boundaries[J]. Journal of Computational Physics, 2006, 215(1):12-40.
[12]THACKER W I, ZHANG J, WATSON L T, et al. Algorithm 905: SHEPPACK: modified Shepard algorithm for interpolation of scattered multivariate data[J]. ACM Transactions on Mathematical Software, 2010(37):1-20.
[13]李宁宇,苏玉民,王兆立,等,三维拍动翼推进效率的计算方法[J].上海交通大学学报,2012, 46(2):323-328.
[14]李宁宇.基于面元法的拍动翼水动力性能计算[D].哈尔滨:哈尔滨工程大学,2012:1-71.
[15]HUNT J C R, WRAY A A. Moin P, Eddies, stream, and convergence zones in turbulent flows, Center for Turbulence Research Report No. CTR-S88[R], Center for Turbulence Research, Stanford, USA, 1988:193-208.
[16]DONG H, MITTAL R, BOZKURTTAS M. Wake structure and performance of finite aspect-ratio flapping foils[C]. //43rd AIAA Aerospace Sciences Meeting, Reno, Nevada, 2005:1-9.
网络出版地址:http://www.cnki.net/kcms/detail/23.1191.U.20151205.2117.006.html
Hydrodynamic analysis and trailing vortex structure of flapping
wings based on the immersed boundary method
LI Ningyu,SU Yumin,LIU Weixing,LIU Peng,CAO Jian
Science and Technology on Underwater Vehicle Laboratory, Harbin Engineering University, Harbin 150001, China
Abstract:At present, the number of studies that have examined the relationship between flapping wing trailing vortex structure and hydrodynamic performance is limited, and the analysis of the effect of parameters is focused on hydrodynamic performance. Parameter simulation for flapping wing and other bionic flows always involves in issues of the complex moving boundary. Self-developed improved immersed boundary method is applied to numerically simulate the non-stationary motion of the flapping wing. Relationship between wing kinematics, vortex dynamics and generation of force is discussed. Results show that the reconstruction algorithm of boundary conditions gives consideration to both calculation efficiency and robustness. The treatment method of the moving boundary developed in this paper can effectively solve the issues related to the moving boundary of the immersed boundary method. Trailing vortex of the 3D flapping wing is constituted by two lines of complex vortex rings. The two lines of complex vortex rings and center line of trailing flow form a dip angle and flow to downstream. Hydrodynamic performance varying with kinematic parameters is decided by the vortex dynamics under the appearance of force production, including the strength and direction of vortex, interconnection of vortex rings and viscous dissipation.
Keywords:flapping wing; immersed boundary method; trailing vortex structure; hydrodynamic performance; propulsion mechanism; incompressible N-S equation
通信作者:李宁宇,E-mail:lny123d@163.com.
作者简介:李宁宇(1986-), 男,博士研究生;
基金项目:国家自然科学基金资助项目(51479039).
收稿日期:2015-08-10.网络出版日期:2015-12-05.
中图分类号:O357.1
文献标志码:A
文章编号:1009-671X(2015)06-026-06
doi:10.11991/yykj.201508009

