供弹系统升降平台的有限元模态分析
郭春阳,胡逢源,祁松,芦晨军,谢婷婷,孙军超
1.哈尔滨工程大学 机电工程学院,黑龙江 哈尔滨 150001
2.上海船舶设备研究所,上海 200031
供弹系统升降平台的有限元模态分析
郭春阳1,胡逢源2,祁松1,芦晨军1,谢婷婷1,孙军超1
1.哈尔滨工程大学 机电工程学院,黑龙江 哈尔滨 150001
2.上海船舶设备研究所,上海 200031
摘要:为改善供弹系统升降平台的动态特性,减小振动对供弹精度以及供弹速度的不良影响,利用有限元软件ANSYS/Workbench建立滚珠丝杠和升降平台的有限元模型并且进行模态分析,在此基础上对升降平台整机进行谐响应分析,得到仿真结果:丝杠的工作转速远小于模态分析中的第一阶固有频率,因此不会发生共振,满足设计的要求;弹箱底板在各阶振型中的振动比较严重,应该增加底板的厚度、减小底板内腔的尺寸从而增加底板的刚度;当外界动载荷的频率接近101 Hz时,振幅迅速增大,振动时系统的应力主要集中在丝杠和轴承接触处、螺母安装座及电机安装底板处,可以通过增加滚珠丝杠的刚度以及螺母和电机安装座的刚度来减小振动幅度。优化了升降平台的设计,提高了抗振能力。
关键词:滚珠丝杠;升降平台;模态分析;谐响应分析;抗振;供弹系统

舰炮作为舰艇的主要作战武器,在反舰作战、对岸火力打击及舰艇防空中具有不可替代的作用。随着现代军事技术的进步及海军战略思想和海战模式的变化,对舰炮的供弹系统提出了更高的要求[1-2]。升降平台是舰炮供弹系统的重要组成部分,为了保证供弹的速率以及其运行的平稳性,要求升降平台具有移动稳定可靠、输送快速安全、出弹平稳和冲击力小的特点。
升降平台采用传统的“伺服电机+滚珠丝杠+支撑轴承+滚动导轨”的方式传动,其运行的平稳性、可靠性及抗振能力都是非常重要的。当系统高速、高加速运动时会产生巨大的动载荷,同时由于海面环境的复杂性,经常会受到海浪、台风等的瞬态冲击,这些动载荷对系统的破坏程度远远高于静载荷的影响,因此,为了保证供弹的速率和供弹系统运行的可靠性从而对升降平台进行振动的模态分析,具有重要的实际意义。
文中采用有限元软件ANSYS/Workbench建立滚珠丝杠和升降平台整机的有限元模型,进行了模态分析,在此基础上对进给系统整机进行谐响应分析,找出引起升降平台振动的原因,并且提出抗振的方法。
1升降平台的方案设计
电梯式升降平台主要负责弹箱在竖直方向上的转运工作。当电梯式升降平台位于最低部时,其恰好与弹库的弹箱储存库衔接,此时接收来自储存库的装有指定种类弹药的弹箱,待弹箱两侧的滑块进入承重台上的滑道的指定位置后,利用前后两个机械锁将其可靠定位,以防止弹箱在移动过程中发生偏移,从而保证能与后续模块准确衔接。电梯式升降平台的传动机构采用丝杠进给伺服机构,能够实现高精度、高效率传动。承重台的一端固定在滚珠丝杠螺母副的螺母上,另一端与滚珠导轨副相连接,在伺服电机的驱动下,螺母带动称重台在竖直方向上移动,从而将弹箱转运到指定位置。电梯式升降平台结构如图1所示。

图1 升降平台结构示意
2模态分析理论基础
模态分析即自由振动分析,是研究结构动力特性的一种近代方法,是最基本的线性动力学分析,用于分析结构的自振频率特性。模态是机械结构的固有振动特性,系统的每一阶模态对应有独立的固有频率、阻尼比和模态振型。模态分析的好处在于可以识别系统的模态参数,避免动载荷频率和系统的某阶固有频率重合发生共振或者利用共振使系统以特定的频率振动,工程师还可以通过分析各阶振型来预知系统在动载荷作用下是如何响应的,参照系统的固有频率有助于在其他动力学分析中设定动态参数。
由经典力学理论可知,物体动力学通用方程为:
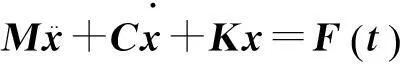
(1)
无阻尼自由振动的运动方程如下表示,其模态分析为方程的特征值和特征向量的求解。

(2)
系统的无阻尼自由振动为简谐振动,其各节点的振动可以用正弦函数表示,即:
(3)
带入式(3)得:
(4)
式(4)是齐次方程,求得的特征向量中各元素只能表示相对比值大小,特征向量没有确定的长度。因此在ANSYS/Workbench模态分析中得到的节点位移云图并不代表系统各部分的实际位移,只是各部分振动的相对关系。
3滚珠丝杠的模态分析
用ANSYS/Workbench进行模态分析建立有限元模型的过程与其他分析过程相似,包括:导入创建几何体、添加材料库、添加模型材料属性、划分网格、施加载荷与约束和结果后处理。但模态分析也有自己的特点,建立模型时需要注意以下几点:
1)模态分析只能是线性分析,对于系统中存在的非线性单元会被处理为线性单元进行分析。对于系统中两部间之间的接触,其刚度值只取决于其设定的初始值,在分析的过程中不会改变。
2)模态分析中材料定义杨氏模量和密度,这是由于系统部件的刚度和质量直接影响模态参数。
3)对于不被完全约束的系统或系统中的部件,模态分析会检测到系统的刚性位移,对应的模态频率在0Hz附近,称为刚体模态。
4)系统的边界条件将直接影响模态分析结果,因此必须准确识别系统的边界条件,认真考虑系统及各部件间是怎么约束的[6- 7]。
电机通过联轴器联接将旋转运动改变为直线运动,丝杠不断地旋转产生一个周期性的载荷,此变载荷的存在使丝杠的变形和应力等状态与静载荷大不相同,因此对丝杠进行模态分析和谐响应分析是必要的。在ANSYS/Workbench中建立丝杠的有限元模型,并进行网格划分,边界条件为一端固定一端支撑。由于螺母在丝杠中间位置时,滚动导轨副对丝杠的支撑作用,使得丝杠的振动主要集中在螺母和支撑轴承之间,丝杠的跨度变小,固有频率增高,因此在螺母位于丝杠一侧时的固有频率要低于螺母位于丝杠中间时的固有频率。对弹箱在平台一侧时的丝杠进行模态分析。图2为螺母位于丝杠一侧时的前四阶模态振型图。
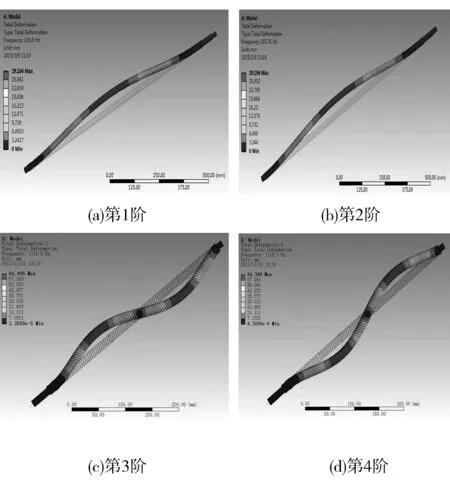
图2 螺母位于丝杠一侧时丝杠前四阶模态振型图
对螺母位于丝杠一侧时进行模态分析,分别分析了前4阶固有频率和振型。
丝杠的固有频率f与其对应的临界转速满足公式n=60×f。其固有频率和对应的临界转速如表1所示。
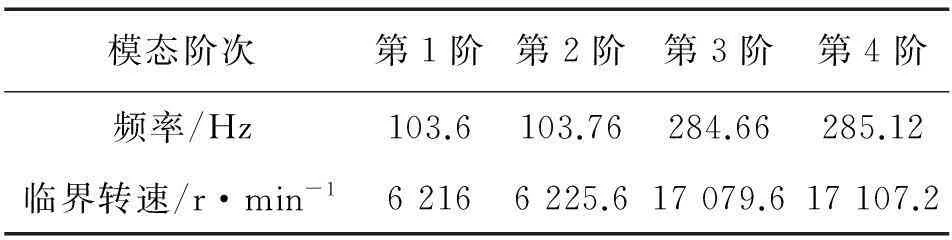
表1 丝杠固有频率和临界转速表
升降平台工作时丝杠的最大转速为1 500 r/min,对比表1中的临界转速,可以看出丝杠的工作转速远小于模态分析中的第一阶固有频率,因此不会发生共振,满足设计的要求。
对于文中选用的丝杠的一阶固有频率对应的转速远大于丝杠实际工作的转速的情况,为了降低成本,可以选用直径稍小的丝杠,同时也可减小轴承结合面、丝杠螺母结合面的接触刚度等。
4升降平台有限元建模
结合升降平台的结构特点,建立有限元模型时,要考虑以下方面问题:局部细节处理、网格划分、结合面的处理。
1)局部细节处理
升降平台模型中包含很多小特征,如倒角、小螺纹孔、光孔等,这些小特征会造成局部网格划分过密,甚至造成网格划分错误,影响分析计算效率,也对整个系统的动态特性影响很大,为了使网格划分后单元网格的形状和密度合理,提高分析结果的精度和可靠性,同时减少计算时间,因此在建立升降平台有限元模型前需要对模型进行等效简化。
2)网格划分
对于三维几何来说,ANSYS/Workbench有几种不同的网格划分方法,例如:自动网格划分、四面体网格划分、扫掠法、多区法等。
本有限元模型采用的是自动网格划分和扫掠法结合的网格划分方法。合理控制网格密度,在不影响计算精度的条件下减少计算时间。升降平台有限元模型网格划分后如图3所示。

图3 升降平台有限元模型
3)结合面的处理
结合面的动态特性常用接触刚度和接触阻尼描述,对于螺栓联接、轴承内圈与轴、轴承外圈与轴承座等固定结合面,由于其接触刚度数量级比结合面高出1~2个数量级,因此在ANSYS/Workbench中将其视为刚性联接。而滚珠丝杠螺母副结合面、支撑轴承结合面及滚动导轨副结合面处滚珠的接触刚度在ANSYS/Workbench中不能通过刚性联接来模拟,否则会引入附加刚度,可用弹簧单元法来模拟[8]。弹簧单元的刚度值,查阅相关资料阻尼系数设为0.1。
5升降平台模态分析结果
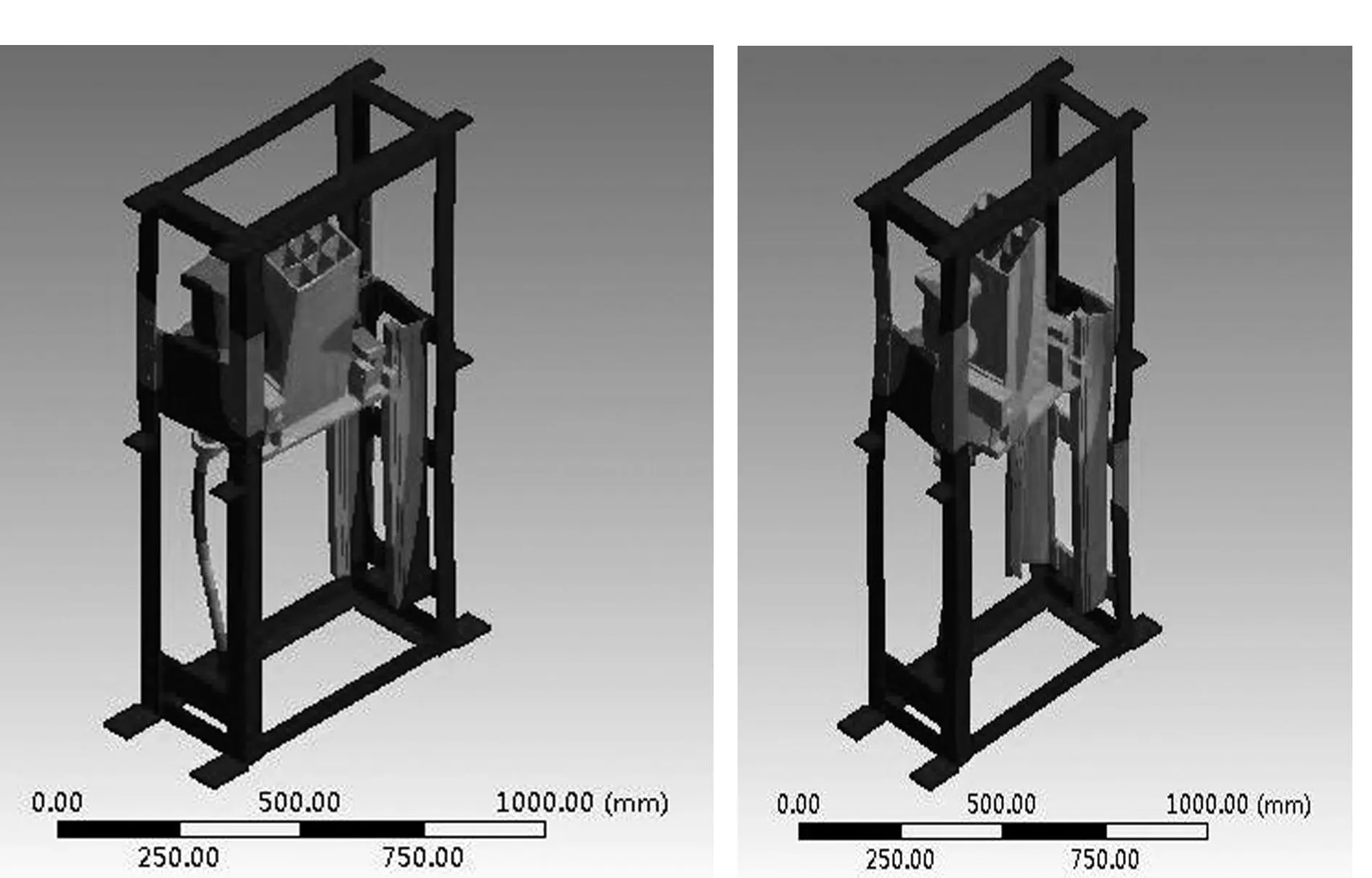
为了模拟升降平台样机的实际安放条件,升降平台的有限元模型的边界条件为安装架底面被施加全约束以及中间和顶部施加部分约束。同时为了研究结合面对升降平台整机动态特性的影响,分别对考虑结合面接触刚度(柔性结合面)和不考虑结合面接触刚度(刚性结合面)情况下整机的动态特性进行分析。不考虑结合面影响时,在ANSYS/Workbench中将2个零件的结合面直接粘合在一起。计算得到的前六阶固有频率分别列于表2中,与其对应的以节点综合位移云图表示的振型图如图4、5。

表2 结合面刚性联接和柔性联接时整机前6阶固有频率
(a) 第1阶 (b)第2阶
(c)第3阶 (d)第4阶
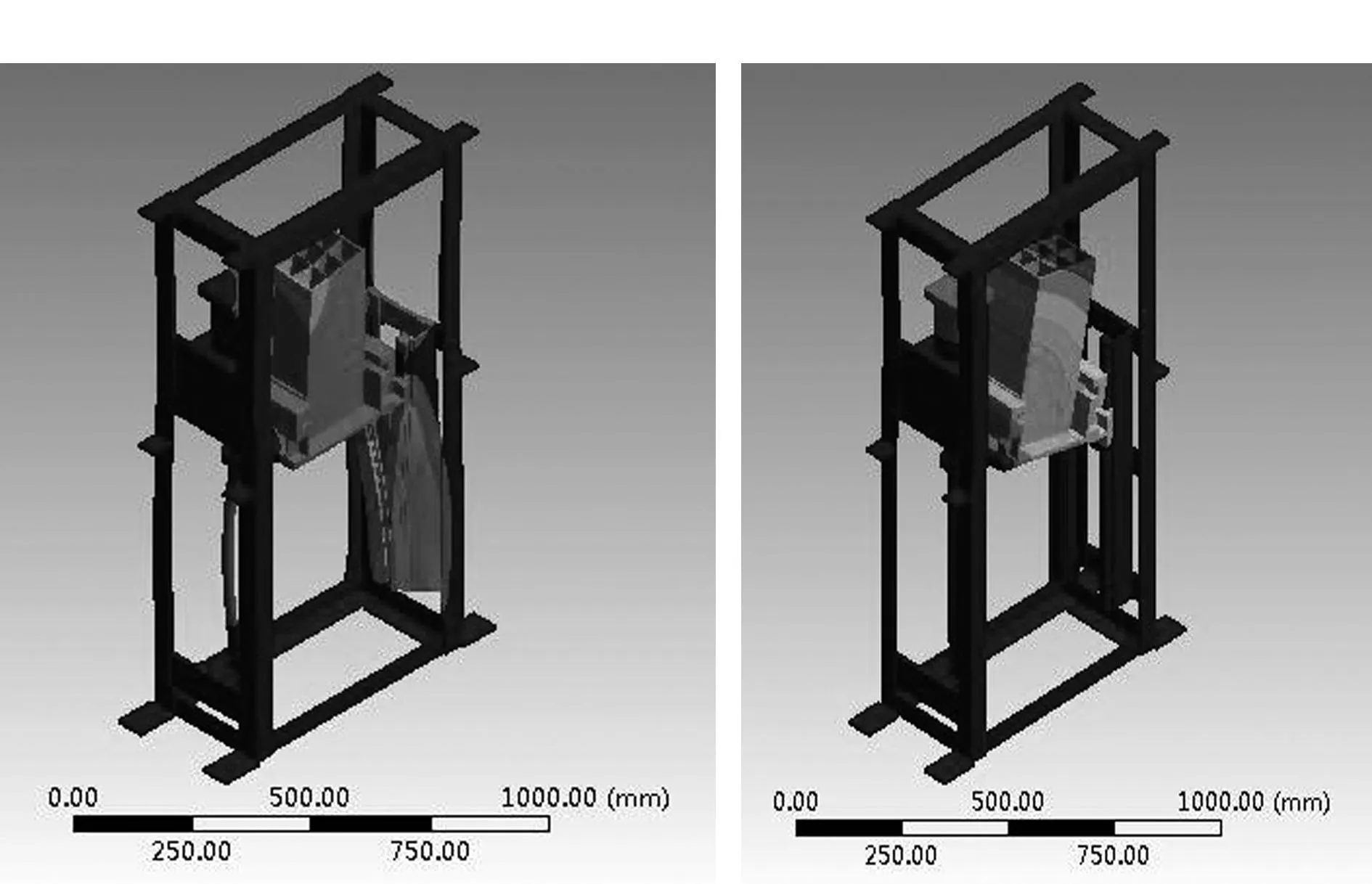
(e)第5阶 (f)第6阶图4 结合面刚性联接时整机前6阶振型图
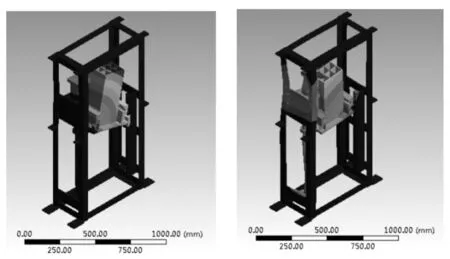
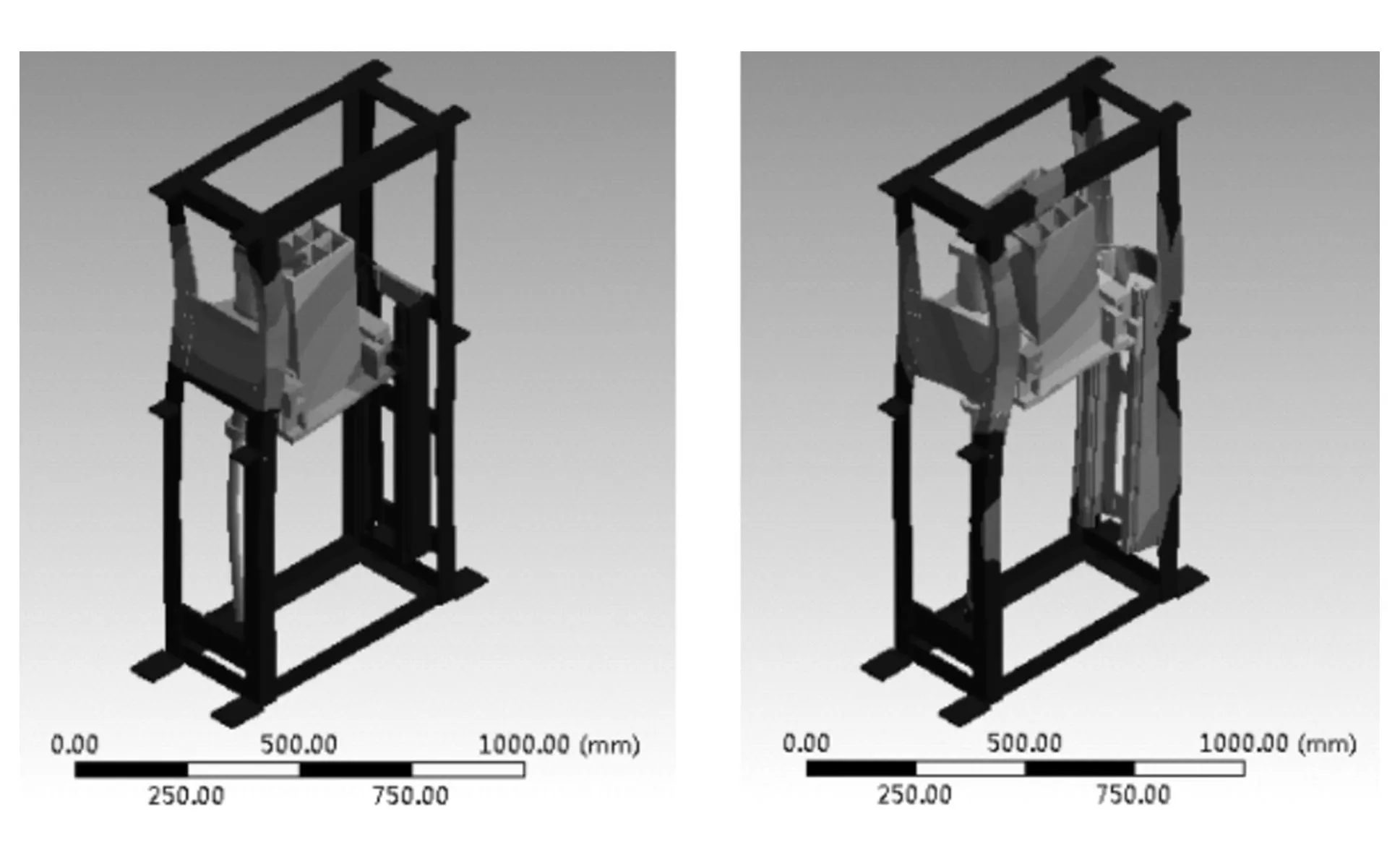
(a) 第1阶 (b)第2阶
(c)第3阶 (d)第4阶

(e)第5阶 (f)第6阶图5 结合面柔性联接时整机前6阶振型图
对比表2中刚性结合面和柔性结合面情况下计算的整机固有频率可知,刚性结合面情况下计算的整机固有频率比柔性结合面情况下的固有频率高出很多,基本上都高出70%。
对比图4和图5中的振型图以及表2中的各阶振型描述可知,各阶振型相差都比较大,由此可知,对升降平台进行模态分析时,是否将结合面上的接触刚度融入整机的动力学模型中,对模态分析结果中的固有频率和振型影响都很大。
从柔性联接的模态分析结果可知:第1阶固有频率分别为38.9 Hz,因此要通过提高丝杠螺母副以及导轨副的接触刚度来提高第1阶的固有频率。升降电梯的支撑机构几乎不发生振动,说明这部分的刚度足以抵抗低频振动,满足系统需要。弹箱底板在各阶振型中的振动比较严重,应该增加底板的厚度、减小底板内腔的尺寸从而增加底板的刚度。系统的第1阶固有频率(基频)是衡量系统动态性能好坏的一个重要指标,采取措施提高第1阶固有频率对升降平台整机的抗振性很有必要。
从整机的模态分析可知,升降平台的整机动态
特性不仅与自身的结构有关,而且与各部分的结合面的接触刚度和边界条件有很大关系。因此对于分析升降平台的整机动态特性,建立准确的结合面动力学模型来模拟结合面特性是非常重要的[9-10]。
6升降平台模态分析结果
谐响应分析也称为频率响应分析或者扫频分析,它是一种特殊的时域分析,计算结构在正弦激励(激励随时间呈正弦规律变化)作用下的稳态振动,也就是受迫振动分析。
结构在简谐载荷作用下受迫振动的微分方程为:
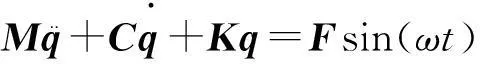
(5)
若节点位移响应为:
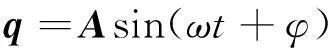
(6)
式中:A为节点振动位移幅值向量;φ为位移响应落后简谐激励的相位角。
将式(5)带入式(6)可得:
利用有限元软件求解,设定ω的频率范围和频率间隔,定义谐波载荷F的大小,从而可以得出若系统受到大小为F、频率为ω的谐波载荷时,某节点振动的位移幅值,由节点的位移幅值和系统材料的杨氏模量,进而可以求得该点的应力。
文中已经对升降平台进行了模态分析,得到了升降平台的各阶固有频率和振型,通过分析固有频率和振型,只能推断出系统共振时各部件的相对振动情况。
在外界动载荷激励下,系统的振动是各阶模态的线性叠加,但不同外载荷时各阶振型对系统的影响程度是不同的,因此需要对升降平台进行谐响应分析,通过谐响应分析结果就可以直观的看出在动态激励下系统各部分的响应及抗振性能。
设定分析情况F=-100 N为作用在螺母上,谐响应分析激振频率的范围为10~140 Hz,因为滑块的振动直接反应升降平台的抗振性能和精度,谐响应分析计算出滑块上一点X、Z方向上振动的位移如图6和图7所示。
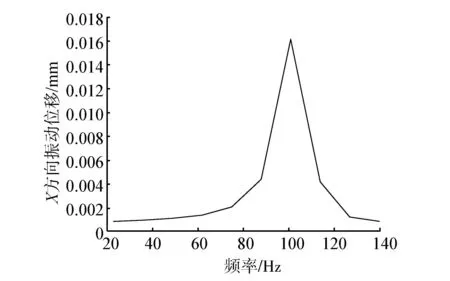
图6 X方向振动位移

图7 Z方向振动位移
图6、7表明:当外界动载荷频率和系统固有频率相差较大时,系统处于弹性控制区,振幅的幅度主要受系统刚度影响,此时提高系统刚度可以减小系统的振动幅度;当外界动载荷的频率接近101 Hz时,与模态分析中的第一、二阶固有频率接近时,振幅迅速增大,X方向上振动峰值为16 μm,Z方向的振动峰值为20 μm。图8表明平台丝杠螺母的安装,使得另一侧弹箱振动的最大位移量为16 μm,从图9可看出,振动时系统的应力主要集中在丝杠和轴承接触处、螺母安装座及电机安装底板处。可通过增加滚珠丝杠的刚度以及螺母和电机安装座的刚度来减小振动幅度,提高系统抗振能力。
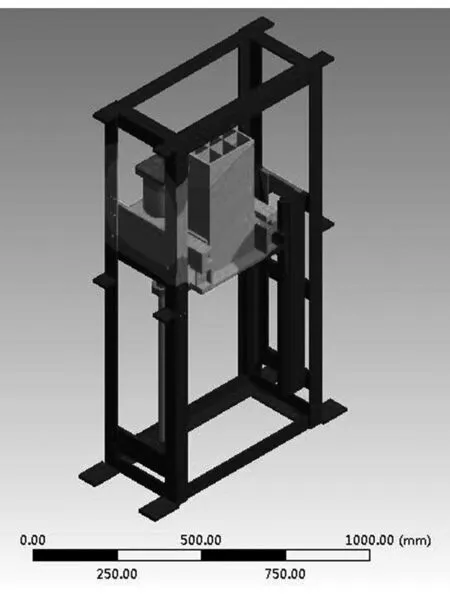
图8 系统位移云图

图9 系统应力云图
7结束语
舰炮供弹系统各个部位在工作过程中存在较大振动,这直接影响舰炮的供弹精度以及供弹速度,通过模态分析的理论与仿真可以找到振动的原因以及振动较为严重的部位,然后提出抗振的方法。升降平台是目前最新提出的结构,简单可靠,但是由于采用滚珠丝杠以及滑轨机构,因此升降平台的振动研究在理论上和实用上都具有很重要的意义。此文只是对其进行仿真分析,如果想更真实的了解其存在的振动问题,还需要进行样机制造以及实验研究。
参考文献:
[1]陈汀峰. 对舰炮发展的思考[J]. 舰船科学技术, 2007, 29(S1): 3-10.
[2]邱志明, 孙世岩, 易善勇, 等. 舰炮武器系统技术发展趋势研究[J]. 舰船科学技术, 2008, 30(2): 21-26.
[3]傅志方, 华宏星. 模态分析理论与应用[M]. 上海: 上海交通大学出版社, 2000: 1-56.
[4]梁霭民, 杨媛媛. 基于车架的振动模态方法应用研究[J]. 电脑知识与技术, 2012, 8(24): 5878-5881.
[5]曹树谦. 振动结构模态分析[M]. 天津: 天津大学出版社, 2001: 5-20.
[6]陈艳霞, 陈磊.AnsysWorkbench工程应用案例精通[M]. 北京: 电子工业出版社, 2012: 112-125.
[7]凌桂龙, 丁金滨, 温正.AnsysWorkbench13.0从入门到精通[M]. 北京: 清华大学出版社, 2012: 100-118.
[8]蒋书运, 祝书龙. 带滚珠丝杠副的直线导轨结合部动态刚度特性[J]. 机械工程学报, 2010, 46(1): 92-99.
[9]李少远. 大口径舰炮弹库出弹平台进给系统动态特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2013: 54-63.
[10]于天彪, 王学智, 关鹏, 等. 超高速磨削机床主轴系统模态分析[J]. 机械工程学报, 2012, 48(17): 183-188.
网络出版地址:http://www.cnki.net/kcms/detail/23.1191.U.20151206.0936.002.html
Finite element modal analysis on the
elevating platform of ammunition feed system
GUO Chunyang1,HU Fengyuan2,QI Song1,LU Chenjun1,XIE Tingting1,SUN Junchao1
1. College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China
2. Shanghai Marine Equipment Research Institute, Shanghai 200031, China
Abstract:In order to improve the dynamic characteristics of the elevating platform of an ammunition feed system and to reduce the bad effect of vibration on the accuracy of ammunition feed and the speed of ammunition feed, the finite element software ANSYS/Workbench is used to establish a finite element model of ball screw and lift platform and do modal analysis. On this basis, by doing harmonic response analysis on complete machine of the platform, the simulation result is obtained. The simulation results: the working speed of screw is much less than the inherent frequency at the first stage in modal analysis, and thus the resonance is not going to happen, meeting the design requirement; the vibration of the bottom plate of ammunition box is serious in all stages and vibration types, and the thickness of bottom plate should be increased and size of cavity of bottom plates should be reduced, to increase the rigidity of bottom plate; when the frequency of the external dynamic load is close to 101 Hz, the amplitude increases rapidly, and during vibration, the stress of system is mainly focused on the connection position of screw and bearing, platform for installing nut and bottom plate for installing electrical machines. By increasing the rigidity of ball screw and platform for installing nut and electrical machine, the amplitude can be reduced. The design of the elevating platform is optimized and shockproof ability is enhanced.
Keywords:ball screw; elevating platform; modal analysis; harmonic response analysis; shockproof; ammunition feed system
通信作者:郭春阳,E-mail:guochunyang@hrbeu.edu.cn.
作者简介:郭春阳(1991-),男,硕士研究生.
基金项目:国家自然科学基金资助项目(NO.51175099).
收稿日期:2015-03-22.网络出版日期:2015-12-06.
中图分类号:TJ818
文献标志码:A
文章编号:1009-671X(2015)06-020-06
doi:10.11991/yykj.201503020

