广义线性模型Lasso惩罚回归估计的局部二次逼近

顾光同

（浙江农林大学 理学院统计系，浙江 临安 311300）

0 引言

广义线性模型（Generalized Linear Model,简称GLM）首先由Nelder和Baker(1972)[1]提出，McCullagh和Neleder(1989)[2]系统地阐述了相关理论框架。此模型经典线性模型的拓展，线性回归模型（Linear Model,简称LM）仅仅是其的一个特例。GLM主要在LM上的拓展主要表现在两个方面：（1）通过设定一个联接函数将被解释变量的期望与解释变量的线性组合连接起来；（2）模型的误差分布不再仅仅要求高斯分布，只需要被解释变量Y的分布为经典指数分布族即可。因此，GLM既适用于大量连续型的Y建模，也适用于大量离散型的Y，这也是GLM自被提出起学术界在理论研究和应用方面受到广泛关注的原因。众所周知，数据建模中模型的待估参数是否能得到有效地估计一直是核心问题，GLM的待估参数通常采用极大似然法（简称ML）来实现估计。本文从Park M Y,Hastie（2007）[3]等提出的GLM的Lasso惩罚即1-范数约束估计路径的基础上，采用Wang（2007）[4]提出的局部二次逼近方法推导得GLM似然函数Lasso惩罚的最小二乘类的参数估计——重复加权最小二乘(RWLS)估计路径。

1 广义线性模型简介

记X是n×k的设计阵，Y是n×1的随机被解释向量，β是未知k×1的参数向量，f(·)表示某种函数形式，u是n×1的随机误差向量，则GLM形如：

模型（1）有下面3个特点（分别用a，b，c列出）：

a.随机误差 u满足 E(u)=0n×1，Y的条件期望μY|X=E(Y|X=xn×k)=f(Xβ) 是 系 统 部 分 即 线 性 预 测ηn×1=Xn×kβk×1=β1+β2x1+...+βkxk的光滑可逆函数，存在连接函数 g(μ)=f-1(Xβ)=η；

b.X和Y的样本观测值既可是连续数据，也可是离散数据；

c.模型的随机部分即Y的分布只需满足典型指数分布族即可，此分布族覆盖了大部分常见分布，比如离散型的Poisson分布和二项分布，连续型的高斯分布、指数分布和Gamma分布等，该分布族的概率密度函数形如：

其中b(·)和c(·)为已知函数，ξ和φ分别为自然参数和刻度参数。

本文先从无惩罚的模型（1）参数向量β的ML估计开始，讨论在Lasso惩罚下的ML估计，并进一步采用局部二次逼近的方式，将其转化为最小二乘估计类。

2 GLM的极大似然估计

2.1 无惩罚极大似然估计

模型（1）的参数向量 β的估计，通常采用ML估计获得，假设被解释变量Y服从指数族分布形如（2），构建形如（1）的GLM，且Y的抽样样本的观测值为y=(y1，y2，...，yn)T，则Y 的对数似然函数为

2.2 LASSO惩罚下的极大似然估计

根据Rosset和Zhu（2007）[6]的研究可知，式（12）的估计路径不是逐片线性的，而最小二乘估计类路径满足逐片线性。下面主要讨论将式（12）逼近为最小二乘估计类的方法。

3 LASSO惩罚回归估计的局部二次逼近

GLM的模型（1）如果采用式（12）直接求解，迭代复杂功效低，Efron和Hastie等（2004）[7]提出的最小角回归（LARS）是求解式（12）的有效算法，要求路径逐片线性。式（11）中的惩罚部分引入单位向量 ei=(0，…，0，1，0，…，0)T，写成另外一种形式为

为了提高效率，尽量避开在Newton-Raphson迭代中去计算式（22），通过对（22）两边取数学期望且因损失函数与极大似然函数相差一个符号，故可用负的Fisher信息阵代替海赛矩阵D的期望。那么在无惩罚的极大似然估计的迭代式（10）中加入惩罚矩阵，再将式（8）-（9）代入可得极大似然的Lasso惩罚的参数向量β的迭代估计路径为

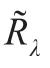
另外，Lasso惩罚系数λ通常是基于Golub、Michael和Grace（1979）提出的广义交叉验证（GCV）方法构造相应的准则实现其最优选择的[3-6]，其他的准则还有BIC准则等可见文献[8]。

4 结束语

广义线性模型的应用越来越广，这是因为模型的随机部分的分布可能满足Gaussian分布、二项式、Poisson分布以及Gamma分布等的一大类指数族。而Lasso惩罚在模型中能有效地同时实现自变量的自动选择和参数估计。本文从无惩罚的GLM的极大似然形式开始，逐步引入Lasso惩罚估计，并基于Lasso惩罚下损失函数的两次泰勒展开实现二次近似，推导和讨论了GLM的极大似然Lasso惩罚估计的最小二乘估计类的路径。在实践应用中，如果GLM的连接函数是典型连接即g(μ)=μ=η时，利用（23）式可得参数向量 β 的估计为 β^=(XTX+R~λ)-1XTY，显然，此时若惩罚矩阵R~λ为0矩阵即相当于模型无惩罚（λ=0）情形下，β^就是普通最小二乘估计而已。由于篇幅有限本文估计方法的模拟和实证等研究笔者将另文阐述。

[1]Nelder J A,Baker R J.Generalized linear models[M].John Wiley&Sons,Inc.,1972．

[2]McCullagh P,Nelder J A.Generalized Linear Models[M].（2th ed）.London:Chapman and Hall,1989.

[3]Park M Y,Hastie T.L1-Regularization Path Algorithm for Generalized Linear Models[J].Journal of the Royal Statistical Society:Series B(Statistical Methodology),2007,69(4).

[4]Wang Y.Maximum Likelihood Computation Based on the Fisher Scoring and Gauss-Newton Quadratic Approximations[J].Computational Statistics and Data Analysis,2007,(8).

[5]Park M Y,Hastie T.L1-Regularization Path algorithm for Generalized Linear Models[J].Journal of the Royal Statistical Society:Series B(Statistical Methodology),2007,69(4).

[6]Rosset S,Zhu J.Piecewise Linear Regularized Solution paths[J].The Annals of Statistics,2007.

[7]Efron B,Hastie T,Johnstone I,et al.Least angle Regression[J].The Annals of statistics,2004,32(2).

[8]Wang H,Leng C.Unified LASSO Estimation by Least Squares Approximation[J].Journal of the American Statistical Association,2007,102(479).