产品服务双合作联盟的最优收益分配研究

冯庆华，陈菊红，刘 通赵益维

（1.西安理工大学 经济与管理学院，西安 710054；2.西安财经学院 信息学院，西安 710100）

0 引言

随着科学技术的高度普及和信息技术的快速传播，制造企业生产的产品在功能和特性等方面的差异日趋缩小。伴随着传统制造业生产能力的急剧膨胀，大多数产品已出现了饱和甚至过剩的状态，使得制造商生产的产品平均利润率持续下降。与此同时，顾客不再满足于对产品的需求，而希望制造企业能够提供更多的基于产品全生命周期的个性化服务。于是很多制造型企业将其业务向服务领域延伸，服务逐渐成为制造企业争夺客户的主要竞争来源。目前国内的一些大型制造企业通过实施服务化战略，延伸了价值链，实现了价值增值和竞争优势的提升。本文基于双合作博弈建立了服务型制造模式下产品服务双合作联盟的收益分配模型，来研究制造企业的最优产品和服务收益分配问题。

1 产品服务的双合作博弈模型

1.1 双合作联盟

服务型制造模式下，作为系统集成商的制造企业将每个集成解决方案进行分解，外包给上游的其他的制造商，所有制造商既提供产品又提供服务，建立了产品服务的双合作联盟。

定义1：设市场上有n个制造企业，用 N={1，2，…，n}表示，3N={(S，T):S，T⊆N，S∩T=∅}表示制造企业形成的双合作联盟集合。对于双合作联盟(S，T)，S中制造企业既提供产品又提供服务,T中的制造企业既不提供产品也不提供服务,N(S∪T)中的制造企业只提供产品不提供服务。b(S，T)表示该双合作联盟获得的收益，b(N，∅)表示所有制造企业均提供产品和服务时获得的总收益。b(∅，N)表示所有制造企业既不提供产品也不提供服务时的收益或损失，一般为零或为负。

定义2：设双合作联盟中的制造企业i获得的服务收益为 yi，产品收益为zi，令xi=yi+zi表示企业i∈N的产品服务收益。根据双合作博弈核心的定义，产品服务双合作联盟的最优收益须满足核心的条件，即：

1.2 双合作联盟的偏序关系

定义3：设两个双合作联盟(A，B)和(C，D)，(A，B)和(C，D)具有可比性等价于(A，B)⊑(C，D) 或(C，D)⊑(A，B)，且满足(A，B)⊑(C，D)⇔A⊆C，B⊇D，我们就说(A，B)和(C，D)具有偏序关系。此外，(A，B)⊏(C，D)⇔A⊆C，B⊃D表示双合作联盟(A，B)是(C，D)的真子集。(A，B)和(C，D)的并(A，B)∨(C，D)=(A∪C，B∩D)，(A，B)和(C，D)的交(A，B)∧(C，D)=(A∩C，B∪D)。

1.3 双合作联盟的最大链和韦伯集

定义4：设Θ(3N)表示双合作联盟的最大链的集合，则双合作联盟的最大链可表示为：

双合作联盟的最大链必须满足以下4条性质：①(∅，N)是最大链的第一个元素；②(N，∅)是最大链的最后一个元素；③相邻的两个双合作联盟 (Sj，Tj)和(Sj+1，Tj+1)之间不存在任何的双合作联盟(M，N),使得(Sj，Tj)⊏(M，N)⊏(Sj+1，Tj+1) 。④每个最大链中包含了2n+1个双合作联盟。

此外，当N={1，2，…，n}，Λ:3N→2Nˉ满足Λ(S，T)=S∪{-i:i∈(NT)} ，则 Nˉ={-n，…，-1，1，…，n}，2Nˉ={S:S⊆Nˉ}表示Nˉ中的制造企业组成的合作联盟的集合。对于双合作联盟的最大链，根据Λ(S，T)=S∪{-i:i∈(NT)}，可得到合作联盟的最大链：

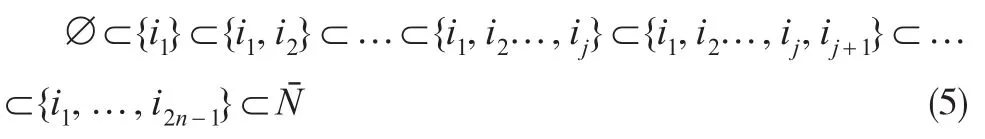
双合作博弈中的最大链体现了双合作联盟的动态变化过程，通过Λ函数将双合作博弈中的所有参与者N={1，2，…，n}转变为了合作博弈下的所有参与者Nˉ={-1，1，-2，2，-3，3}，说明了双合作博弈是合作博弈的一个特例。

下面给出一个双合作联盟最大链的例子。

例 1：设 制 造 企 业 的 集 合 N={1，2，3} ，根 据Λ(S，T)=S∪{-i:i∈(NT)}，则 Nˉ={-3，-2，-1，1，2，3},存在如下的一个双合作联盟的最大链：

对于这个最大链中的每一个元素,根据Λ(Sj，Tj)=θ(ij)，则 Λ(∅，(1，2))= θ(i1)={-3}, Λ(∅，(1))=θ(i2)={-3，-2}，Λ(∅，∅)=θ(i3)={-3，-2，-1},Λ((3)，∅)=θ(i4)={-3，-2，-1，3}, Λ((3，2)，∅)=θ(i5)={-3， -2，-1，3，2}。在2Nˉ上可得到如下的最大链：

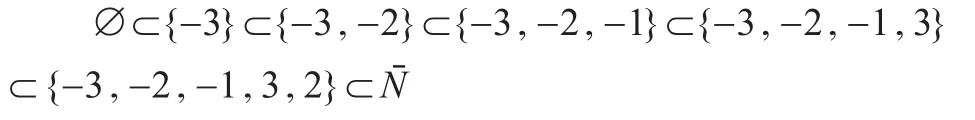
Λ函数将制造企业的双合作联盟转变为了合作联盟，实际上是根据制造企业提供的要素把双合作联盟S中既提供产品又提供服务的制造企业拆分为合作联盟中提供产品的企业（用负数表示）和提供服务的企业（用正数表示）。例如 Λ((3，2)，∅)={-3，-2，-1，3，2}中，双合作联盟((3，2)，∅)表示制造企业3和制造企业2既提供产品又提供服务，制造企业1只提供产品不提供服务。根据Λ函数转变为了合作联盟{-3，-2，-1，3，2}，实际上是将双合作联盟中的制造企业3和2（既提供产品又提供服务）拆分为了合作联盟中的企业3和2（提供服务）和企业-3和-2（提供产品），由于制造企业1只提供产品，所以在合作联盟中用企业-1表示。

1.4 具有超模性的双合作联盟相关定理

Bilbao[7]进一步证明了如下的收益递增定理和核心与韦伯集相等的定理。定理1：当双合作联盟函数满足超模性：

此定理说明了当双合作联盟函数满足超模性时，对于任何一个制造企业，参与的产品服务双合作联盟越大，边际收益越大。

定理2：满足超模性的双合作联盟的核心非空，并且核心与韦伯集相等。

证明：由于双合作联盟的韦伯集是一个非空集合，如果能够证明双合作联盟的韦伯集包含在核心中，并且核心也包含在韦伯集中，则此定理得证。

设 (S，T)∈3N，但不包含在θ序中，且满足Λ(S，T)={i1，i2，…，ik}，k=n+s-t，

Λ-1[θ(i1)]⊏Λ-1[θ(i2)]⊏…⊏Λ-1[θ(ik)] ，设A0=∅，Aj={i1，i2，…，ij} ，1≤j≤k，则 有Aj=Λ(S，T)∩Λ(Λ-1[θ(ij)]),即 Λ-1(Aj)=(S，T)∩Λ-1[θ(ij)]。根据定理1，当双合作联盟满足超模性时，则有b(Λ-1[θ(ij)])-b(Λ-1[θ(ijij)])≥b(Λ-1(Aj))-b(Λ-1(Aj-1))。

所以可得出，当双合作联盟满足超模性时，韦伯集中所有的边际向量都包含在核心中。

2 应用算例

假设一个集成解决方案所组成的供应链由3个制造企业组成，分别是二层产品服务提供商、一层产品服务提供商和系统集成商。分别用1,2,3表示，这3个制造企业组建的双合作联盟的过程形成了一个最大链，即

(∅，N)⊏(∅，(1，2))⊏(∅，(1))⊏(∅，∅)⊏((3)，∅)⊏((3，2)，∅)⊏(N，∅)

其中，(∅，N)表示这3个制造企业刚开始既不提供产品也不提供服务，(∅，(1，2))表示制造企业3选择退出T,为客户提供产品；(∅，(1))表示制造企业2选择退出T,为客户提供产品；(∅，∅)表示制造企业1选择退出T,为客户提供产品,此时3个制造企业都为客户提供产品。随着服务型制造模式的出现，制造企业开始施行了服务化战略，首先实施服务化战略的是制造企业3，此时它不仅提供产品还提供服务。((3)，∅)表示制造企业3选择为客户提供产品还提供服务；((3，2)，∅)表示制造企业2选择为客户提供产品也提供服务；(N，∅)表示制造企业1也选择为客户提供产品也提供服务，此时3个制造企业均为客户提供产品和服务。

根据Λ(S，T)=S∪{-i:i∈(NT)}将上述双合作联盟的最大链转换为：

∅⊆{-3}⊆{-3，-2}⊆{-3，-2，-1}⊆{-3，-2，-1，3}⊆{-3，-2，-1，3，2}⊆{-3，-2，-1，3，2，1}

设最大链中的双合作联盟的收益分别为b(∅，N)=0，b(∅，(1，2))=60 ， b(∅，(1))=110 ， b(∅，∅)=150 ，b((3)，∅)=230 ，b((3，2)，∅)=300 ，b(N，∅)=360（单位：万元）。可以看出，包含在最大链中的任何两个双合作联盟都是满足超模性的，因此，根据韦伯集的定义，可得：

z3=b(Λ-1{-3})-b(Λ-1{∅})=b(∅，(1，2))-b(∅，N)=60 z2=b(Λ-1{-3，-2})-b(Λ-1{-3})=b(∅，(1))-b(∅，(1，2))=50 z1=b(Λ-1{-3，-2，-1})-b(Λ-1{-3，-2})=b(∅，∅)-b(∅，(1))=40 y3=b(Λ-1{-3，-2，-1，3})-b(Λ-1{-3，-2，-1})=b((3)，∅)-b(∅，∅)=80 y2=b(Λ-1{-3，-2，-1，3，2})-b(Λ-1{-3，-2，-1，3})=b((3，2)，∅)-b((3)，∅)=70 y1=b(Λ-1{-3，-2，-1，3，2，1})-b(Λ-1{-3，-2，-1，3，2})=b(N，∅)-b((3，2)，∅)=60

其中yi表示制造企业i的服务收益，zi表示制造企业i的产品收益，双合作联盟的收益分配结果如表1所示。

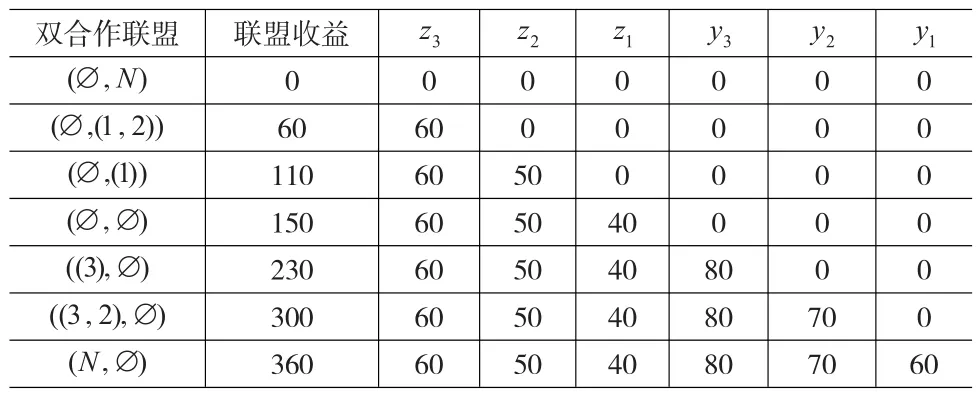
表1 产品服务双合作联盟的最优收益分配表 （单位：万元）

由此可得出，双合作联盟中制造企业1的收益为x1=y1+z1=60+40=100，制造企业2的收益为x2=y2+z2=70+50=120，制造企业3的收益为x3=y3+z3=80+60=140。

3 结论

制造企业为了寻求新的竞争优势，满足客户的个性化需求而实施了服务化战略。在服务型制造模式下，供应链中的制造企业不仅提供产品还提供服务。在进行收益分配时，不仅要考虑产品的收益也要考虑服务的收益。本文根据服务化转型下供应链收益分配的特点，建立了双合作博弈模型证明了收益定增定理和核心非空定理，进一步根据韦伯集是核心的子集求解出了制造企业产品服务双合作联盟的最优收益分配结果。今后还将会对双合作联盟收益函数的构建、考虑到企业的不同服务质量对服务收益分配的影响等方面做进一步的深入研究。

[1]Gillies D B.Some Theorems on N-person Games[M].Princeton:Princeton University Press,1953.

[2]Weber R J.Probabilistic Values for Games.In:Roth AE(ed)The Shapley Value:Essays in Honer of Lloyd S.Shapley[M].Cambridge:Cambridge University Press,1988.

[3]Shapley L S.Cores of Convex Games[J].Int.Journal of Game Theory,1971,(1).

[4]王利,张有志,周嫄媛.三级供应链合作利润博弈模型及经济性分析[J].运筹与管理,2009,18(4).

[5]王晓萍,赵晓军.基于博弈论的逆向供应链合作利润分配研究[J].工业技术经济,2007,26(11).

[6]孟炯,唐小我,倪得兵.基于利润分配的制销供应链联盟安全责任策略[J].管理工程学报,2010,24(1).