Constructing the Cocyclic Structures for Crossed Coproduct Coalgebras

CHEN QUAN-GUoAND WANG DING-GUo

(1.School of Mathematics and Statistics,Yili Normal University,Yining,Xinjiang,835000)

(2.School of Mathematical Sciences,Qufu Normal University,Qufu,Shandong,273165)

Communicated by Du Xian-kun

Constructing the Cocyclic Structures for Crossed Coproduct Coalgebras

CHEN QUAN-GUo1AND WANG DING-GUo2

(1.School of Mathematics and Statistics,Yili Normal University,Yining,Xinjiang,835000)

(2.School of Mathematical Sciences,Qufu Normal University,Qufu,Shandong,273165)

Communicated by Du Xian-kun

In this paper,we construct a cocylindrical object associated to two coalgebras and a cotwisted map.It is shown that there exists an isomorphism between the cocyclic object of the crossed coproduct coalgebra induced from two coalgebras with a cotwisted map and the cocyclic object related to the diagonal of the cocylindrical object.

Hopf algebra,crossed coproduct coalgebra,cocyclic object

1 Introduction

From the perspective of duality,it is necessary to consider the cocyclic structures of some coalgebras.It is the starting point of this paper to construct the cocyclic structures of crossed coproducts with invertible cotwisted maps,of which twisted smash coproducts in sense of Wang and Li[5]are special cases.

This paper is organized as follows:In Section 2,we recall the basic concepts of cocylindrical objects.Then crossed products with cotwisted maps are discussed in Section 3.The key content of this paper is to construct cocylindrical objects in Section 4.Finally,It is shown that there exists an isomorphism between the cocyclic object of the crossed coproduct coalgebraA×TBandΔ(A♮TB)the cocyclic object related to the diagonal ofA♮TBIn Section 5.

2 Cocylindrical Objects

Let us recall cocyclic objects.IfAis any category,a paracocyclic object inAis a sequence of objectsA0,A1,···together with coface operators∂i:An→An+1(i=0,1,···,n+1), codegeneracy operators,σi:An→An-1(i=0,1,···,n-1)and cyclic operatorsτn:An→An,where these operators satisfy the cosimplicial conditions and the following extra relations:

A bi-paracocyclic object in a categoryAis a double sequenceA(p,q)of objects ofAand operatorsandsuch that for allp≥0,q≥0,

are paracocyclic objects inAand every horizontal operator commutes with every vertical operator.We say that a bi-paracocyclic object is cocylindrical,if for allp,q≥0,

Throughout this paper,we works over a feldk.All algebras and coalgebras are overk. The undecorated tensor product⊗means tensor product overk.LetCbe a coalgebra.We use Sweedler’s notation: where summation is omitted.

3 Crossed Coproducts with Cotwisted Maps

Let(A,ΔA,εA)be a coalgebra and(B,ΔB,εB)be a coalgebra.Give a linear mapT:ThenA⊗Bhas the coproduct:

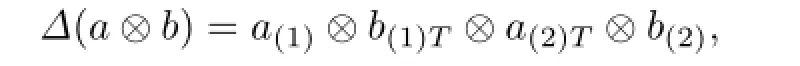
wherefor allb∈B,a∈A.We say thatA⊗Bis a crossed coproduct which is denoted byA×TB,ifA⊗Bis a coalgebra with the counitεA⊗εB.In this case,the mapTis called a cotwisted map.

Lemma 3.1Using the notation as above,A×TB is a crossed coproduct if and only if the following conditions hold:for all a∈A and b∈B,

4 The Cocylindrical ObjectA♮TB

In what follows,we always assume that the cotwisted mapTis invertible,and its inverse is denoted byT-1.

Lemma 4.1The cotwisted map T satisfes(3.1)-(3.3)if and only if its inverse T-1satisfes the following identities:for all a∈A and b∈B,

Example 4.1LetBbe a Hopf algebra with the invertible antipodeSandAbe a leftB-comodule coalgebra.Defne the cotwisted map

Then we have the crossed coproduct coalgebraA×TBwith the coproduct

Note that the cotwisted mapTis invertible,and its inverseT-1is

Example 4.2[5]LetBbe a Hopf algebra with the invertible antipodeSandAbe aB-bicomodule coalgebra.Let

be left and rightH-comodule structures onA,respectively.Then we have the crossed coproduct coalgebraA×TBwith the coproduct

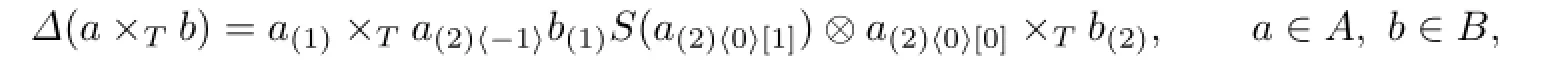
where the cotwisted map

We can check thatTis invertible with its inverseT-1given as follows:

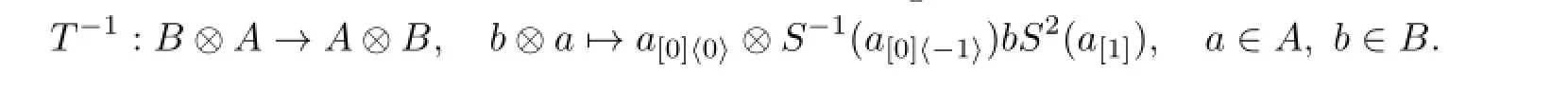
Proof.For alla∈Aandb∈B,we have

So we getT-1◦T=id.AndT◦T-1=id can be checked similarly.

For the sake of convenience of expression,forai∈A,bi∈B,i,j∈N,we denote

Now we introduce the cocylindrical module

whereA,Bare both coalgebras andTis a cotwisted map.We defne the operators∂p,q, σp,q,τp,qand¯∂p,q,¯σp,q,¯τp,qas follows:for allai∈Aandbj∈B,

where 0≤i≤p,0≤j≤q.

Theorem 4.1Let A and B be both coalgebras,and T an invertible cotwisted map.Then A♮TB with the operators defned above is a cocylindrical object.

Proof.We only check the commutativity of the cyclic operators and the cocylindrical condition.First,we check that every horizontal operator commutes with every vertical operator,that is,τp,q¯τp,q=¯τp,qτp,q.Indeed,for allai∈Aandbj∈B,we have

and

Corollary 4.1For two coalgebras A and B,if the cotwisted map T is invertible,then Δ(A♮TB)is a cocylic object.

5 Relation ofΔ(A♮TB)with the Cocylic Object of the Crossed CoproductA×TB

LetBbe a coalgebra.The cocyclic objectC·(B)is defned byCn(B)=B⊗(n+1),n≥0, with coface,codegeneracy and cyclic operators given by:

Applying the above operations to the crossed coproductA×TB,we have a cocyclic objectC·(A×TB).

Forn∈N,we defne a mapϕn:A♮TB(n,n)→Cn(A×TB),

The following theorem reveals the relations betweenΔ(A♮TB)andC·(A×TB).

Theorem 5.1ϕ={ϕn}n≥0defnes a cocyclic map between Δ(A♮TB)and C·(A×TB).

Proof.We show thatϕcommutes with the cylic and cosimplical operators:

(1)τϕn=ϕnτn,n¯τn,n.In fact,for allai∈Aandbj∈B,we have

and

Also

By comparing the above equations,we can get the desired result.With the same argument,using Lemma 4.1 and with direct computations,we can check that

Theorem 5.2Let A and B be two coalgebras and T an invertible cotwisted map.Then we have an isomorphism of cocyclic objects

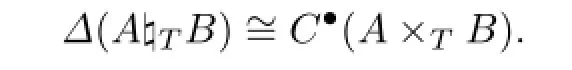
Proof.Forn∈N,we defne a mapφn:Cn(A×TB)→A♮TB(n,n),

Since

So it follows that

can be checked similarly.

[1]Getzler E,Jones J D S.The cyclic homology of crossed product algebras.J.Reine Angew. Math.,1993,445:163-174.

[2]Akbarpour R,Khalkhali M.Hopf algebra equivariant cyclic homology and cyclic homology of crossed product algebras.J.Reine Angew.Math.,2003,559:137-152.

[3]Zhang J,Hu N H.Cyclic homology of strong smash product algebras.J.Reine Angew.Math., 2012,663:177-207.

[4]Carboni G,Guccione J A,Guccione J J,et al.Cyclic homology of Brzezi´nski’s crossed products and of braided Hopf crossed products.Adv.Math.,2012,231:3502-3568.

[5]Wang S H,Li J Q.On twisted smash products for bimodule algebras and the drinfeld double.Comm.Algebra,1998,26:2435-2444.

[6]Connes A.Noncommutative Geometry.New York:Academic Press,1994.

A

1674-5647(2015)01-0081-08

10.13447/j.1674-5647.2015.01.09

Received date:April 9,2013.

Foundation item:The NSF(11261063,11171183)of China,the Fund(2012ZDXK03)of the Key Disciplines in the General Colleges and Universities of Xinjiang Uygur Autonomous Region,the Foundation(2013721043)for Excellent Youth Science and Technology Innovation Talents of Xinjiang Uygur Autonomous Region and the NSF (ZR2011AM013)of Shandong Province.

E-mail address:cqg211@163.com(Chen Q G).

2010 MR subject classifcation:16W30