Existence of Solutions for a Four-point Boundary Value Problem with a p(t)-Laplacian

LI YUAN-XIAo,GAo WEN-JIEAND SoNG WEN-JING

(1.College of Science,Henan University of Technology,Zhengzhou,450001)

(2.Institute of Mathematics,Jilin University,Changchun,130012)

(3.Institute of Applied Mathematics,Jilin University of Finance and Economics, Changchun,130017)

Existence of Solutions for a Four-point Boundary Value Problem with a p(t)-Laplacian

LI YUAN-XIAo1,GAo WEN-JIE2AND SoNG WEN-JING3

(1.College of Science,Henan University of Technology,Zhengzhou,450001)

(2.Institute of Mathematics,Jilin University,Changchun,130012)

(3.Institute of Applied Mathematics,Jilin University of Finance and Economics, Changchun,130017)

This paper deals with the existence of solutions to thep(t)-Laplacian equation with four-point boundary conditions.It is shown,by Leray-Schauder fxed point theorem and degree method,that under suitable conditions,solutions of the problem exist.The interesting point is thatp(t)is a general function.

p(t)-Laplacian,four-point boundary condition,fxed point theorem, Leray-Schauder degree method

1 Introduction

In this paper,we investigate the existence of solutions to the followingp(t)-Laplacian ordinary diferential equations with four-point boundary conditions:

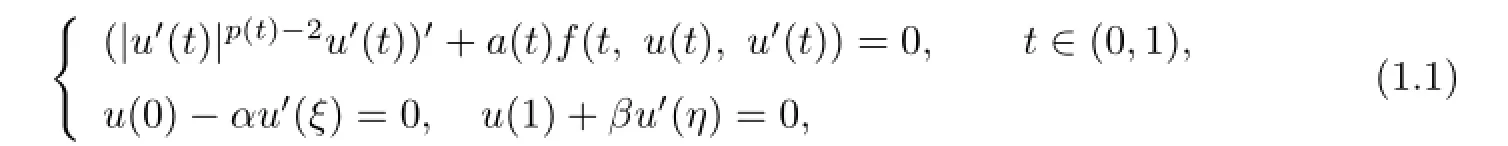
where the functionsf,p,a,and the constantsα,β,ξ,ηsatisfy:

(H1)f∈C([0,1]×R×R,R),p∈C([0,1],R)andp(t)＞1,a∈C((0,1),R)is probably singular att=0 ort=1 and satisfes

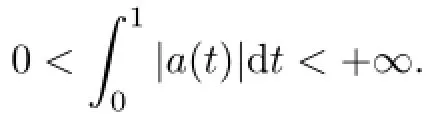
In the recent years,diferential equations and variational problems with variable exponent have been studied extensively,for which the readers may refer to[1-6].Such problems arise in the study of image processing,electrorheological fuids dynamics and elastic mechanics (see[7-10]).

In the case whenpis a constant,the problem(1.1)becomes the classicalp-Laplacian problem.Lian and Ge[11]discussed the following problem:

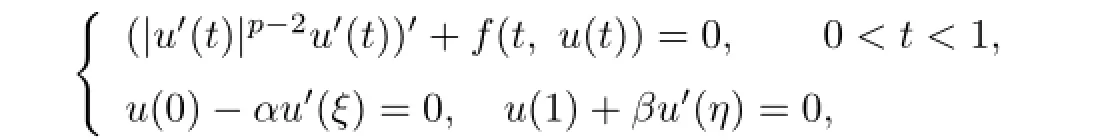
and obtained the existence of multiple positive solutions.For more information about the existence of solutions for ordinary diferential equations withp-Laplacian operator,the interested readers may refer to[12-17]and references therein.

Motivated by the results of the above papers,we study the existence of solutions to the problem(1.1).The main features of this paper are as follows.Firstly,p(t)is a general function,which is more complicated than the case whenpis constant.Secondly,the nonlinear termfmay change sign anda(t)is allowed to be singular att=0 ort=1,which difer from thosep-Laplacian problems.

The outline of this paper is as follows.In Section 2,we give some necessary preliminaries and important lemmas.Sections 3 is devoted to the proof of the existence of solutions to the problem(1.1).

2 Preliminaries

In this section,we give some preliminaries and lemmas.

DefneU=C1[0,1].It is well known thatUis a Banach space with the norm‖·‖1defned by

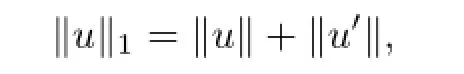
where

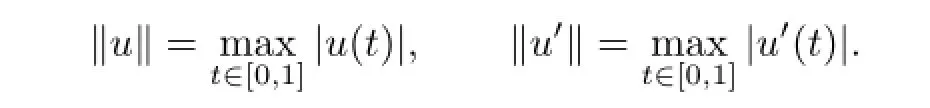
Set

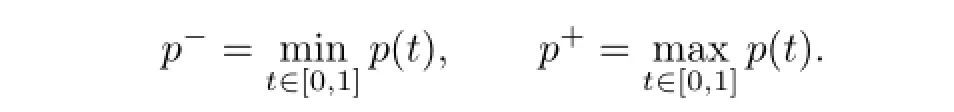
Denote

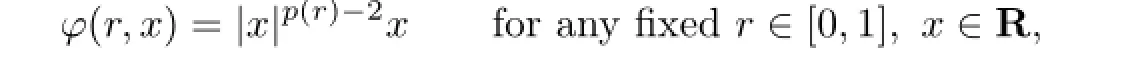
and denoteφ-1(r,·)as

whereφ-1(r,0)=0.

Evidently,φ-1(r,·)is continuous and sends a bounded sets into a bounded sets.

To obtain the existence of solutions of the problem(1.1),we need the following lemmas. The proofs are standard,and we omit the details.

Lemma 2.1Let U be a Banach space.Suppose that the operator T(u,λ):U×[0,1]→U is a map satisfying the following conditions:

(S1)T is a compact map;

(S2)T(u,0)=0for any u∈U;

(S3)If one has u=T(u,λ)for some λ∈[0,1],then there exists an M＞0such that‖u‖U≤M for any u∈U.

Then,T(u,1)has a fxed point in U.

Lemma 2.2Assume that g∈L1[0,1]and g(t)/≡0on any subinterval of[0,1].Then the boundary value problem{

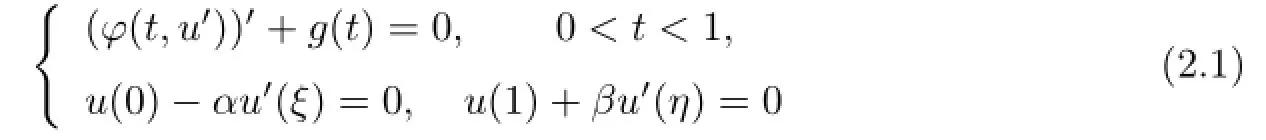
has a unique solution u(t)which is

or

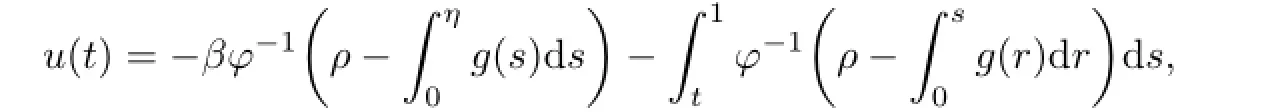
where ρ=φ(0,u′(0))and ρ is dependent of g.

Now,for anyh∈C[0,1],we defne

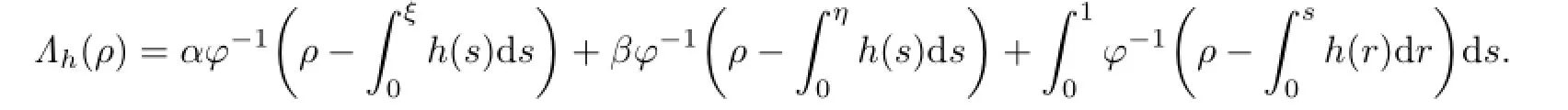
The properties of the operatorΛhis stated in the following lemma.

Lemma 2.3For any h∈C[0,1],the equation

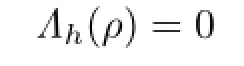
has a unique solution¯ρ(h)∈R.

Proof.The proof is similar to the proof of Lemma 2.1 in[5],and we omit the details here.

Using Lemma 2.2 and Lemma 2.3,we also have the following lemma.

Lemma 2.4If u is the solution of the problem(2.1),then it can also be rewritten in the form as

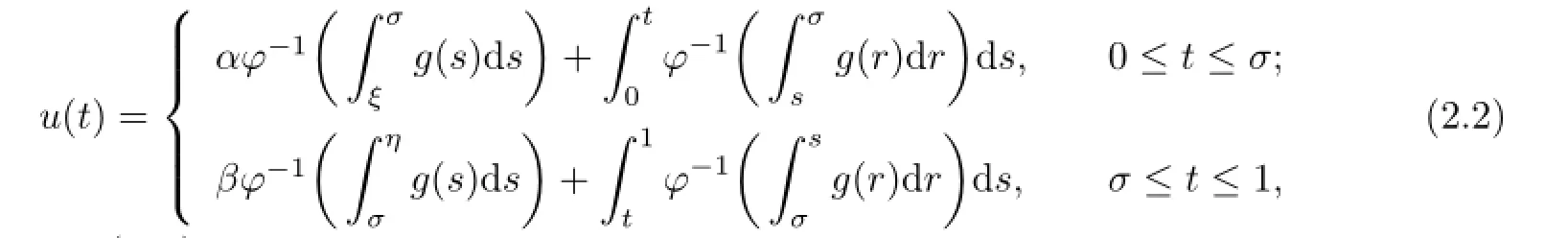
where σ∈(0,1).

Proof.Assume thatu(t)is the solution of the problem(2.1).Then there exists aσ∈(0,1) such thatu′(σ)=0.On the contrary,suppose thatu′(t)＜0 for anyt∈(0,1).We know thatu(t)is nonincreasing.From the boundary value conditions it follows that

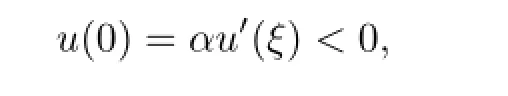
but

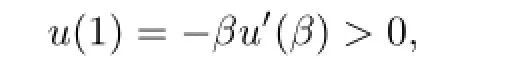
which is a contradiction.Similarly,ifu′(t)＞0 for anyt∈(0,1),we fnd thatu(t)is nondecreasing,which together with boundary conditions yields a contradiction.By direct computations,we see that(2.2)holds.

3 Existence of Solutions

In this section,we show the existence of solutions to the problem(1.1).

Theorem 3.1Assume that(H1),(H2)hold,and f satisfes

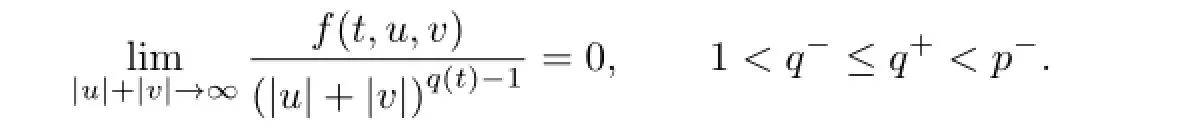
Then the problem(1.1)has at least one solution.

Proof.In order to obtain the existence of solutions of the problem(1.1),we consider the boundary value problem

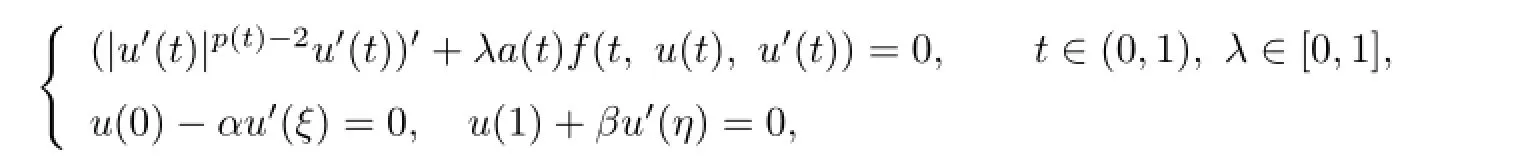
and defne the integral operatorT:U×[0,1]→Uby

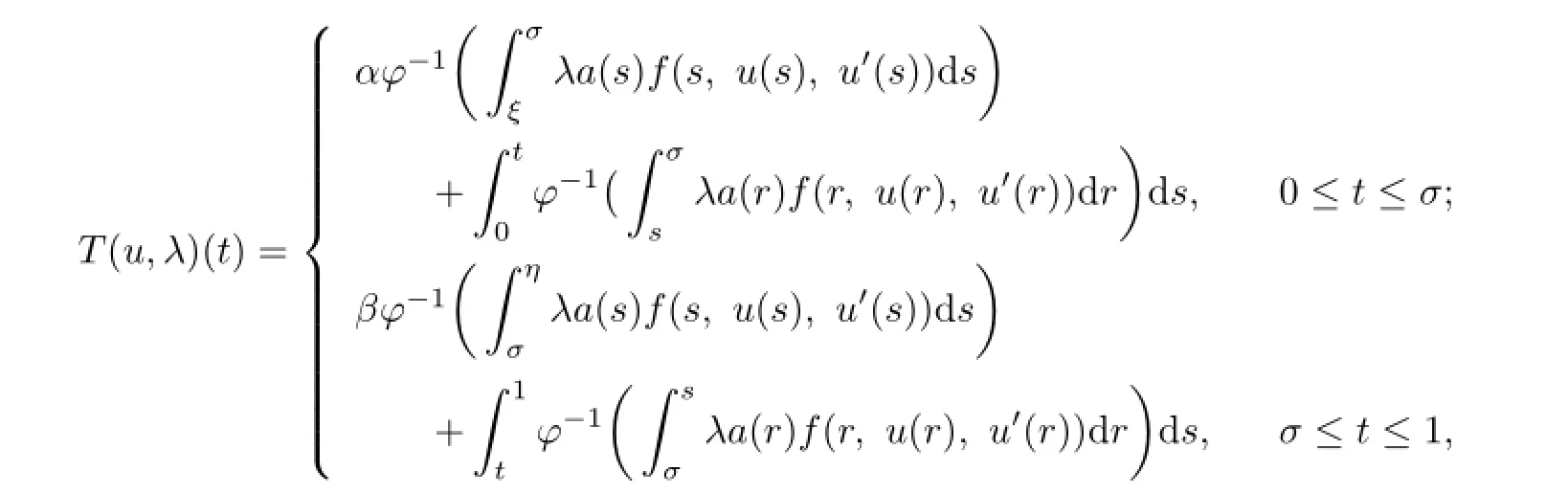
whereσ∈(0,1).From the continuity off,φ-1and the defnition ofa,it is easy to see thatuis a fxed point of the integral operatorTif and only ifuis a solution of the problem(1.1) whenλ=1.In order to apply Lemma 2.1,the proof is divided into three steps.

(1)Tis compact.

LetD⊂U×[0,1]be an arbitrary bounded subset.Then there exists anMsuch that

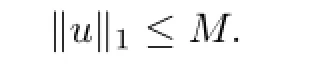
Let{(un,λn)}be a sequence inD.First,we prove that{T(un,λn)}has a convergent subsequence inC[0,1].By the conditions(H1),we know that there exists anN＞1 such that

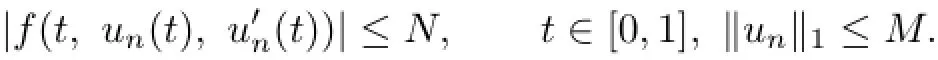
Then for any(un,λn)∈D,if 0≤t≤σ,one has

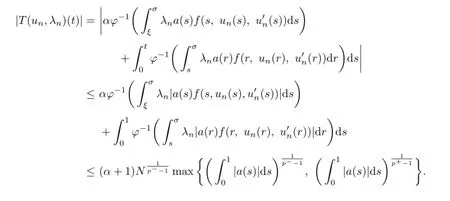
Similarly,ifσ≤t≤1,we conclude that

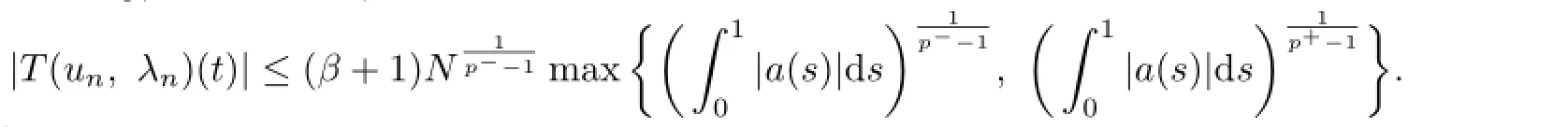
On the other hand,

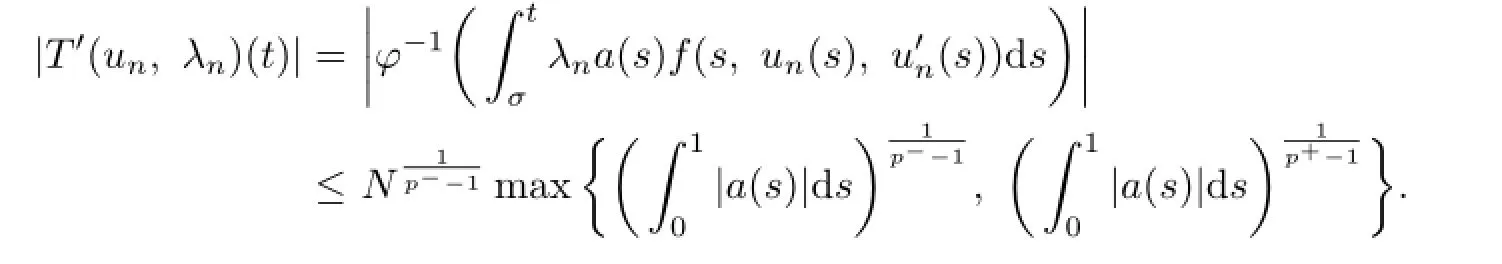
So

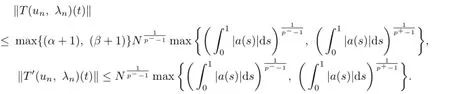
Meanwhile,we fnd that

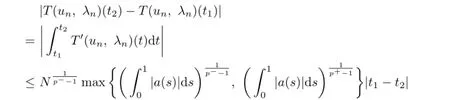
for any 0≤t1≤t2≤1.Hence,{T(un,λn)}is uniformly bounded and equi-continuous. Applying the Ascoli-Arzel`a theorem,there exists a convergent subsequence of{T(un,λn)}inC[0,1],and without loss of generality,we denote again by{T(un,λn)}.

Next,we show that{T′(un,λn)}also has a convergent subsequence inC[0,1].

Denote

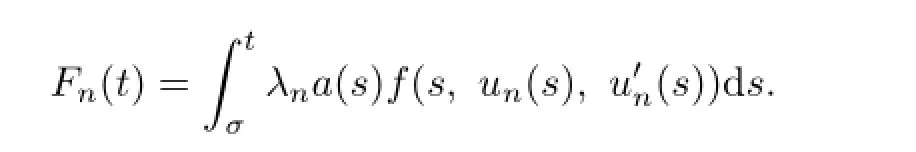
Similarly to the proof above,we know that{Fn(t)}has a convergent subsequence inC[0,1],which we also denote by{Fn(t)}.According to the continuity ofφ-1,we see that{T′(un,λn)}is convergent inC[0,1].Consequently,the condition(S1)in Lemma 2.1 is satisfed.

(2)Obviously,T(u,0)=0 foru∈U,and so the condition(S2)in Lemma 2.1 holds.

(3)We verify the condition(S3)in Lemma 2.1.

If it were false,we would fnd that there exists a subsequence{(un,λn)}such that‖un‖1→∞asn→∞and‖un‖1＞1.Then by Lemma 2.4 we have

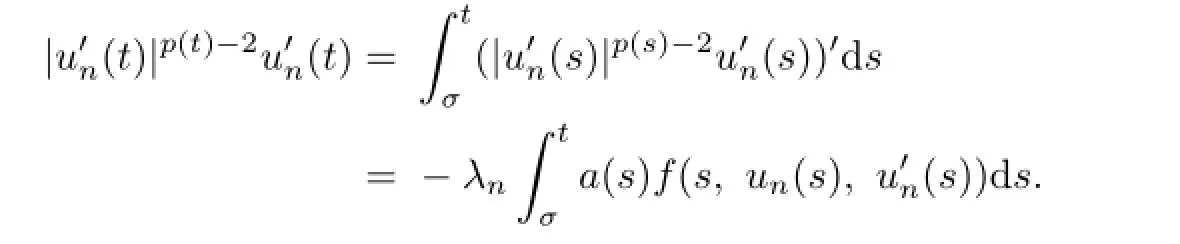
Noting that

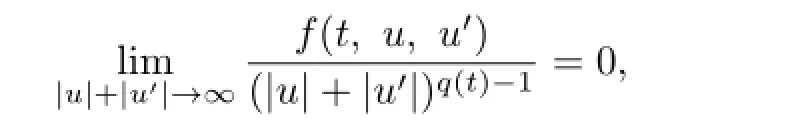
we get that there existM1＞0 andc1＞0 such that

Thus,forandt∈[0,1],we have

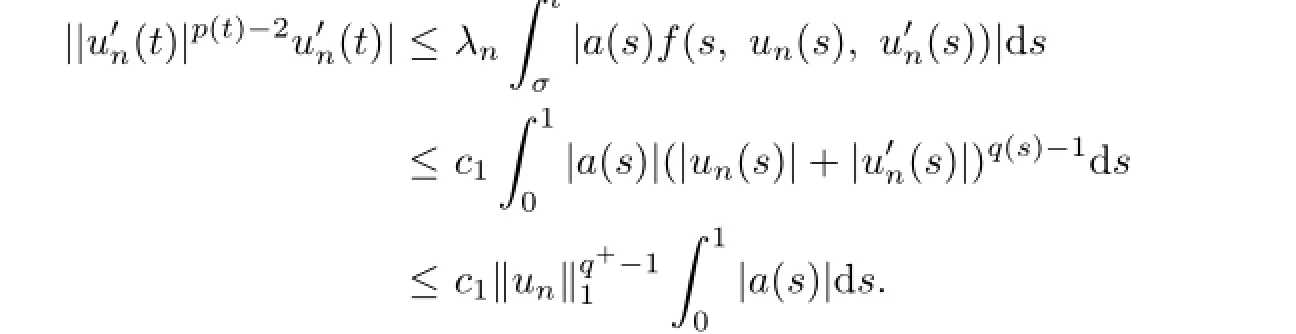
So

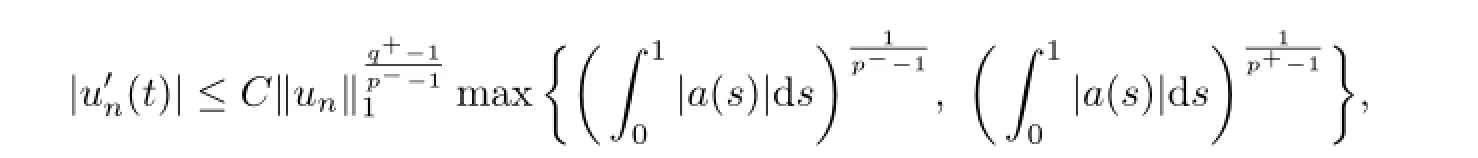
and

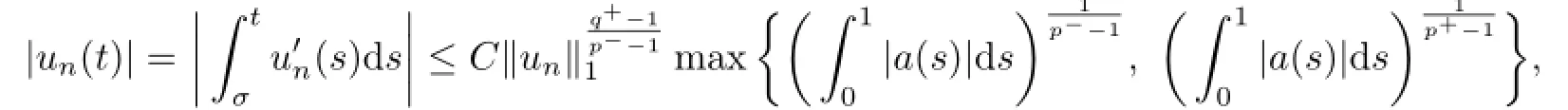
whereCis a constant.

Consequently,we can conclude that{(un,λn)}is bounded,which is a contradiction. Then,the condition(S3)in Lemma 2.1 holds.

Applying Lemma 2.1,we obtain thatT(u,1)has a fxed point inU.Therefore,the problem(1.1)has at least one solution.This completes the proof.

Now,we prove the existence of solutions to the problem(1.1)whenfsatisfes some other conditions.

Theorem 3.2Assume that Ωr={u∈C1[0,1],‖u‖1＜r}is a bounded open set in U and(H1),(H2)hold.Then the problem(1.1)has at least one solution u(t)if there exists an r＞0such that

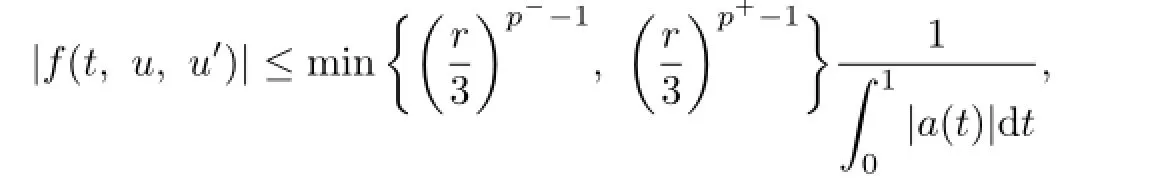
where u∈¯Ωr,t∈[0,1].

Proof.Consider the boundary value problem

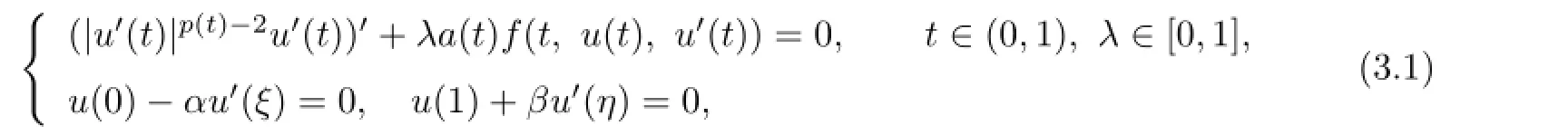
and defne an operatorT:U×[0,1]→Uby

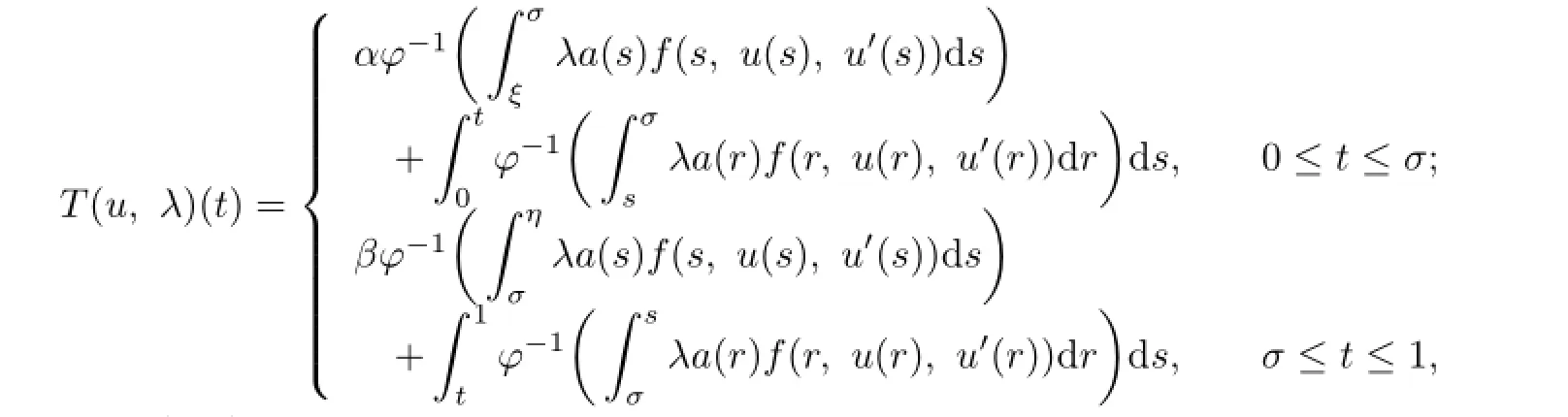
whereσ∈(0,1).ThenTis a compact operator.Moreover,uis a solution of the problem (1.1)if and only ifuis a fxed point ofu=T(u,1).In order to obtain the existence of solutions to the problem(1.1)by Leray-Schauder degree theory,we only need to prove that

(i)u=T(u,λ)has no solution on∂Ωrfor anyλ∈[0,1);

(ii) deg(I-T(u,0),Ωr,0)/=0.

First,we prove that(i)is satisfed.Without loss of generality,if there exists aλ∈[0,1) andu∈∂Ωrsuch thatu=T(u,λ),then

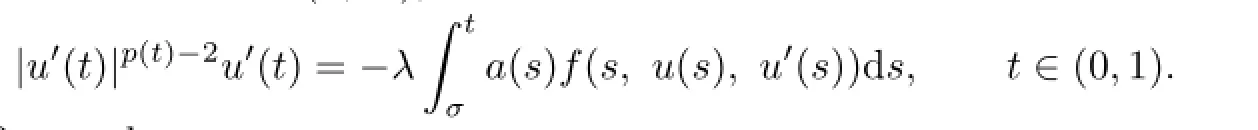
Sinceu∈∂Ωr,one has

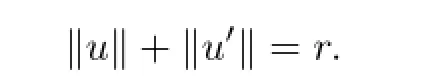
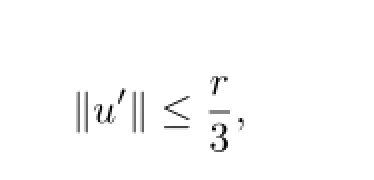
but

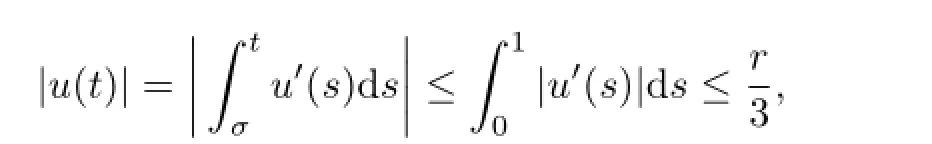
a contradiction.

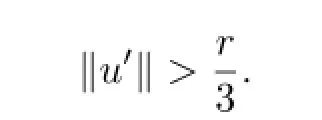
Then there exists somet0∈[0,1]such that

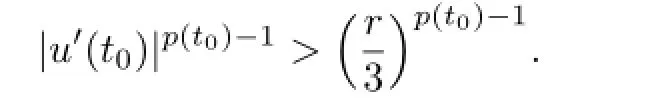
From the condition

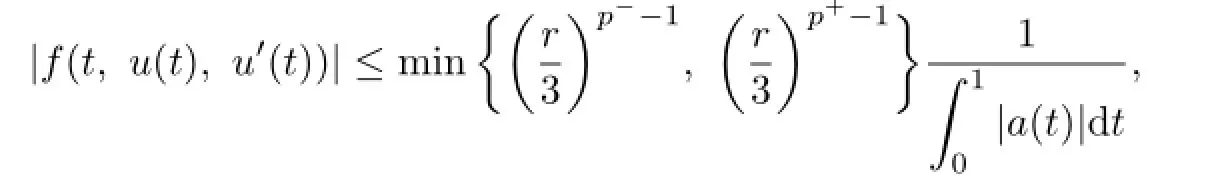
we obtain that

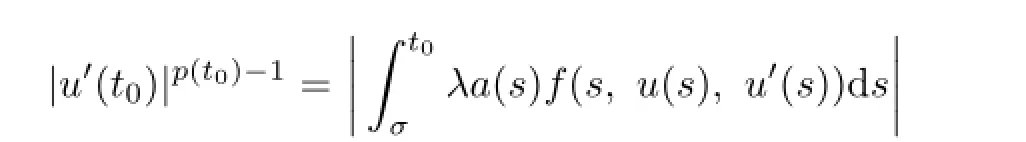
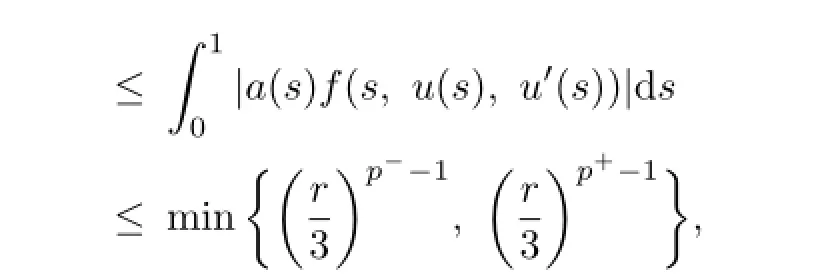
which is again a contradiction.Hence,the problem(3.1)has no solution on∂Ωr.

Next,whenλ=0,it is easy to see that the problem(3.1)has a solution onΩr.Obviously,

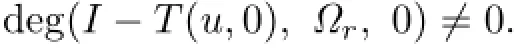
So the condition(ii)holds.

Thus,upon an application of Leray-Schauder degree method,we obtain that the problem (1.1)has at least one solution.

[1]Fan X L,Zhang Q H.Existence of solutions forp(x)-Laplacian Dirichlet probelm.Nonlinear Anal.,2003,52:1843-1852.

[2]Fan X L,Wu H Q,Wang F Z.Hartman-type results forp(t)-Laplacian systems.Nonlinear Anal.,2003,52:585-594.

[3]Harjuleto P,H¨ast¨o P,Koskenoja M.The Dirichlet energy integral on intervals in variable exponent Sobolev space.Z.Anal.Anwendungen,2003,22:911-923.

[4]Musielak J.Orlicz Spaces and Modular Spaces.in:Lecture Notes in Math.1034.Berlin: Springer-Verlag,1983:1-222.

[5]Zhang Q H.Existence of solutions for weightedp(r)-Laplacian system boundary value probelms.J.Math.Anal.Appl.,2007,327:127-141.

[6]Zhang Q H,Liu X P,Qiu Z M.Existence of solutions for weightedp(t)-Laplacian system multi-point boundary value probelms.Nonlinear Anal.,2009,71:3715-3727.

[7]Chen Y,Levine S,Rao M.Variable exponent,linear growth functionals in image restoration.SIAM.J.Appl.Math.,2006,66:1383-1406.

[8]Diening L.Maximal function on generalized Lebesgue spaceLp(·).Math.Inequal.Appl.,2004,7:245-253.

[9]R˙uˇziˇcka M.Electrorheological Fluids:Modeling and Mathematical Theory.in:Lecture Notes in Math.1748.Berlin:Springer-Verlag,2000:16-38.

[10]Zhikov V V.Averaging of functionals of the calculus of variations and elasticity theory.Math. USSR Izv.,1987,29:33-36.

[11]Lian H R,Ge W G.Positive solutions for a four-point boundary value probelm with thep-Laplacian.Nonlinear Anal.,2008,68:3493-3503.

[12]Cabada A,Tomeˇcek J.Extremal solutions for nonlinear functionalϕ-Laplacian impulsive equations.Nonlinear Anal.,2007,67:827-841.

[13]Ji D H,Ge W G,Yang Y T.The existence of symmetric positive solutions for Sturm-Liouvillelike four-point boundary value probelm with ap-Laplacian operator.Appl.Math.Comput., 2007,189:1087-1098.

[14]Liu B F,Zhang J H.The existence of positive solutions for some nonlinear boundary value problems with linear mixed boundary conditions.J.Math.Anal.Appl.,2005,309:505-516.

[15]Man´asevich R,Mawhin J.Periodic solutions for nonlinear systems withp-Laplacian-Like operators.J.Diferential Equations,1998,145:367-393.

[16]Wang Y Y,Ge W G.Existence of multiple positive solutions for multipoint boundary value problems with a one-dimensionalp-Laplacian.Nonlinear Anal.,2007,67:476-485.

[17]Wang Y Y,Ge W G.Multiple positive solutions for multipoint boundary value problems with one-dimensionalp-Laplacian.J.Math.Anal.Appl.,2007,327:1381-1395.

A

1674-5647(2015)01-0023-08

10.13447/j.1674-5647.2015.01.03

Received date:Oct.29,2012.

Foundation item:The NSF(11271154)of China,the Key Lab of Symbolic Computation and Knowledge Engineering of Ministry of Education,the 985 program of Jilin University,and the DR Fund(150152)of Henan University of Technology.

E-mail address:yxiaoli85@yahoo.cn(Li Y X).

2010 MR subject classifcation:34B15,34L30,47H10,47H11