Equivalent Conditions of Complete Convergence for Weighted Sums of Sequences of Extended Negatively Dependent Random Variables
LIU CUN-cHAo,GUo MING-LEAND ZHU DoNG-JIN
(School of Mathematics and Computer Science,Anhui Normal University, Wuhu,Anhui,241003)
Communicated by Wang De-hui
Equivalent Conditions of Complete Convergence for Weighted Sums of Sequences of Extended Negatively Dependent Random Variables
LIU CUN-cHAo,GUo MING-LE*AND ZHU DoNG-JIN
(School of Mathematics and Computer Science,Anhui Normal University, Wuhu,Anhui,241003)
Communicated by Wang De-hui
By using Rosenthal type moment inequality for extended negatively dependent random variables,we establish the equivalent conditions of complete convergence for weighted sums of sequences of extended negatively dependent random variables under more general conditions.These results complement and improve the corresponding results obtained by Liet al.(Li D L,RAO M B,Jiang T F,Wang X C.Complete convergence and almost sure convergence of weighted sums of random variables.J.Theoret.Probab.,1995,8:49-76)and Liang(Liang H Y.Complete convergence for weighted sums of negatively associated random variables.Statist. Probab.Lett.,2000,48:317-325).
extended negatively dependent random variable,complete convergence, weighted sum
1 Introduction
In many stochastic model,the assumption that random variables are independent is not plausible.Many researchers focus on weakening the restriction of independence in recent years.The concept of extended negatively dependent random variables was frstly introducedby Liu[1]as follows.
Defnition 1.1[1]Random variables{Xi,i≥1}are said to be extended negatively dependent if there exists a constant M>0such that both

and
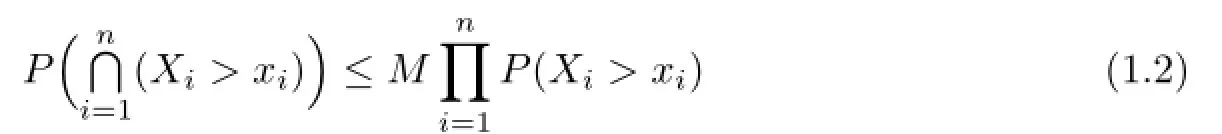
hold for each n≥1and all real numbers x1,x2,···,xn.
In the caseM=1 the notion of extended negatively dependent random variables reduces to the well-known notion of so-called negatively dependent random variables which was introduced by Lehmann[2].Recall that random variables{Xi,i≥1}are said to be positively dependent if the inequalities(1.1)and(1.2)hold both in the reverse direction whenM=1.Not looking that the notion of extended negatively dependent random variables seems to be a straightforward generalization of the notion of negative dependence,the extended negative dependent structure is substantially more comprehensive.As it is mentioned in[1],the extended negatively dependent structure can refect not only a negative dependent structure but also a positive one,to some extend.Joag-Dev and Proschan[3]also pointed out that negatively associated random variables must be negatively dependent,and therefore,negatively associated random variables are also extended negatively dependent. Some applications for sequences of extended negatively dependent random variables have been found.We refer to Shen[4]for the probability inequalities,Liu[1]for the precise large deviations,and Chen[5]for the strong law of large numbers and applications to risk theory and renewal theory.
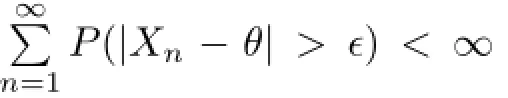
Theorem 1.1[7]Let{X,Xn,n≥1}be a sequence of independent and identically distributed random variables,0<p<2and r>1.Then
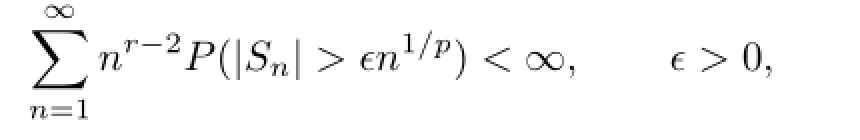
if and only if
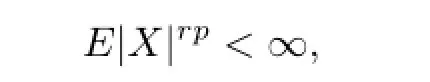
where EX=0whenever1≤p<2.
Since partial sums are particular cases of weighted sums and the weighted sums are often encountered in some actual questions,the complete convergence for the weighted sums seems more important.Liet al.[8]investigated the complete convergence for independent weighted sums and obtained the following result.From now on,we denote always logx= ln(max{e,x}).
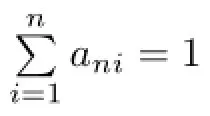
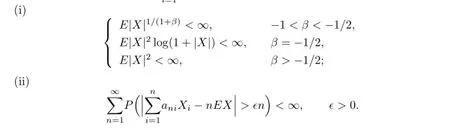
Liang[9]extended the conclusions of Liet al.[8]from independent and identically distributed random variables to identically distributed negatively associated random variables. The result is as follows:
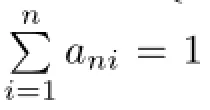

The main purpose of this paper is to generalize and improve the result of Theorem 1.3 to the case of sequences of extended negatively dependent random variables.We investigate the complete convergence for weighted sums of sequences of extended negatively dependent random variables under more general conditions.Equivalent conditions of complete convergence for weighted sums of sequences of extended negatively dependent random variables are established.As a result,we not only promote and improve the results of Liang[9]from negatively associated random variables to extended negatively dependent random variableswithout necessarily imposing any extra conditions,but also relax the range ofβ.As an application,the Baum-Katz type result for sequences of extended negatively dependent random variables is obtained.
Throughout this paper,the symbolCdenotes generic positive constants,whose value may vary from one application to another,andI(A)denotes the indicator function ofA. Letan≪bndenotes that there exists a constantC>0 such thatan≤Cbnfor sufciently largen,and letan≈bnmeanan≪bnandbn≪an.
By Defnition 1.1,the following properties of extended negatively dependent sequences can be obtained directly.
Lemma 1.1Let random variables{Xn,n≥1}be extended negatively dependent.Let {fn,n≥1}be a sequence of Borel functions,all of which are monotonically increasing(or all are monotonically decreasing).Then random variables{fn(Xn),n≥1}are still extended negatively dependent.
The following lemma is the Rosenthal type inequality for extended negatively dependent sequences and is obtained by Shen[4].
Lemma 1.2[4]Let{Xi,i≥1}be a sequence of extended negatively dependent random variables with
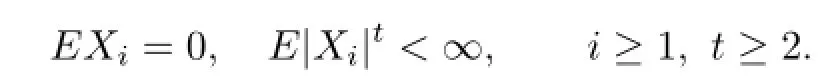
Then there exists a positive constant C depending only on t such that

By Lemma 1.2 and Theorem 3 in[10],we can obtain the following lemma.
Lemma 1.3Let{Xi,i≥1}be a sequence of extended negatively dependent random variables with
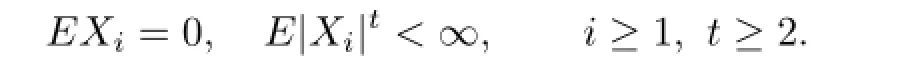
Then there exists a positive constant C depending only on t such that
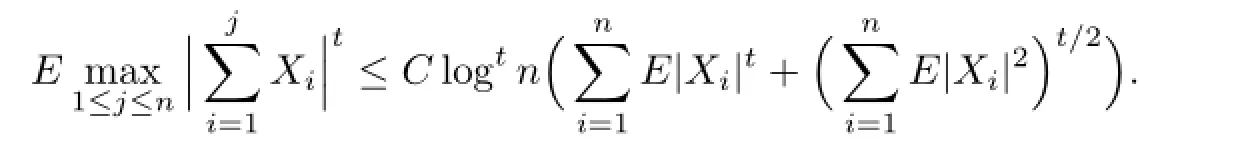
From the proof of Lemma 1.10 in[11]and by Lemma 1.2 we can obtain the following lemma.
Lemma 1.4Let{Xn,n≥1}be a sequence of extended negatively dependent random variables.Then there exists a positive constant C such that
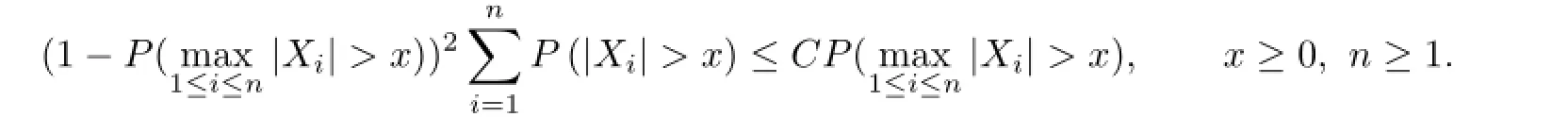
Using Fubini’s theorem,the following lemma can be easily proved.
Lemma 1.5Let X be a random variable.Then
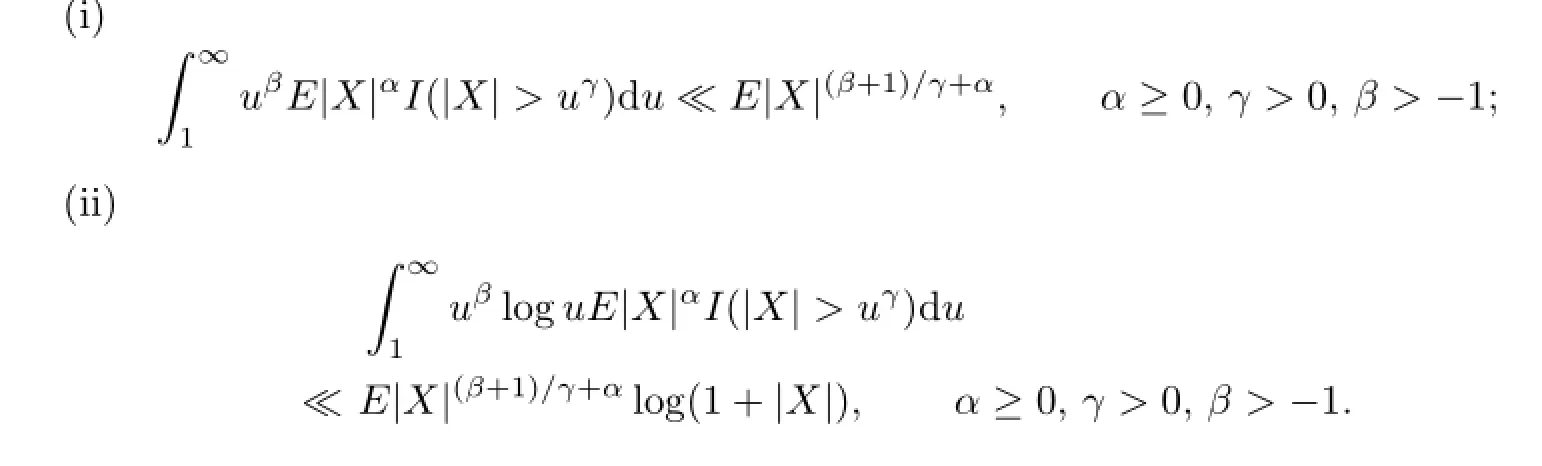
2 Main Results and Proofs
Theorem 2.1Let{X,Xn,n≥1}be a sequence of identically distributed extended negatively dependent random variables,r>1,p>1/2,β+p>0and suppose that EX=0for1/2<p≤1.Let{ani≈(i/n)β,1≤i≤n,n≥1}be a triangular array of real numbers. Then the following are equivalent:
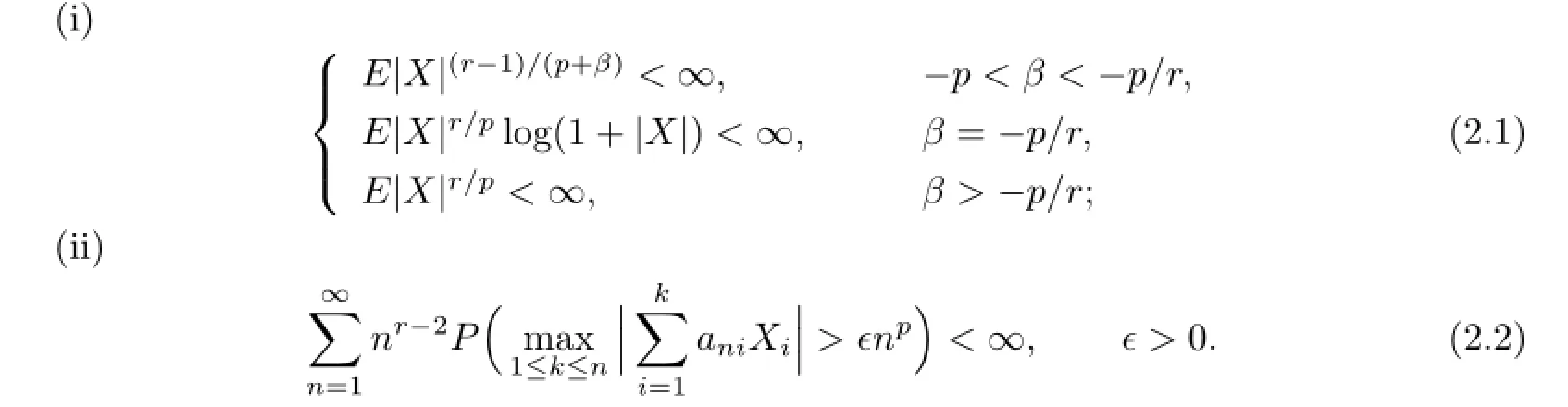
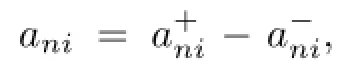

So,without loss of generality,we can assume thatani>0,1≤i≤n,n≥1.Choose aδ>0 small enough and an integerKsufciently large.Set,for any 1≤i≤n,n≥1,
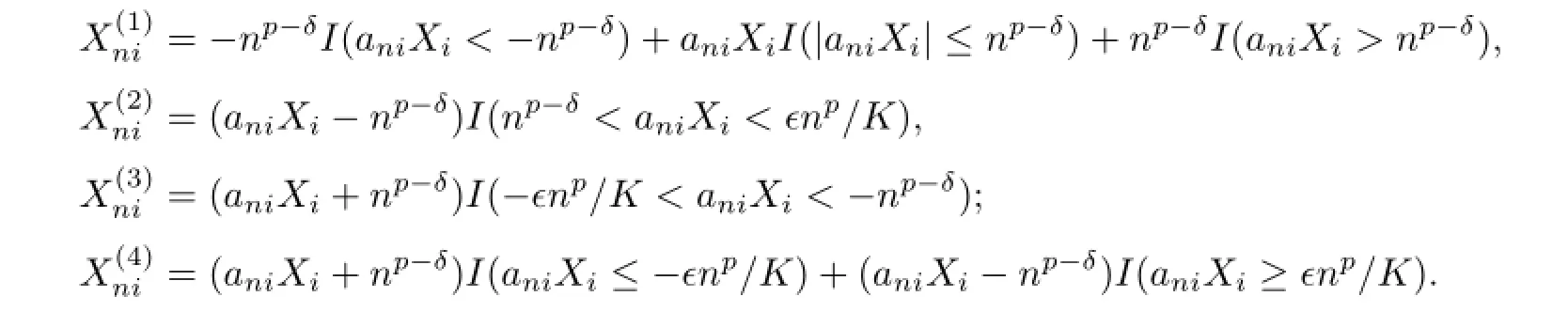
It is obvious that

Note that

Hence,to complete the proof of(2.2),it sufces to show that
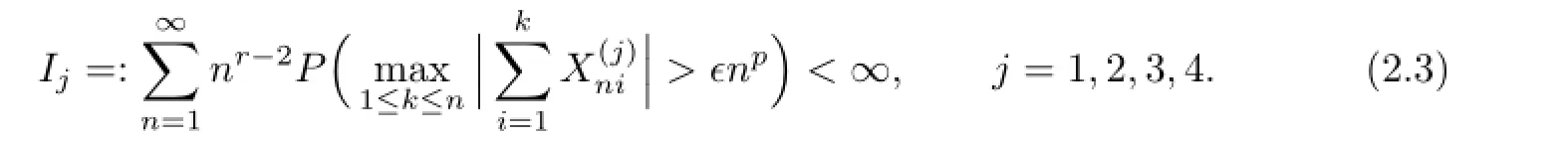
From the defnition ofit is easy to see that
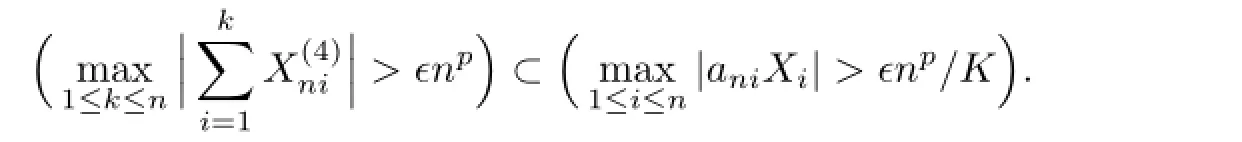
Noting thatani≈(i/n)β,we obtain from Lemma 1.5 that
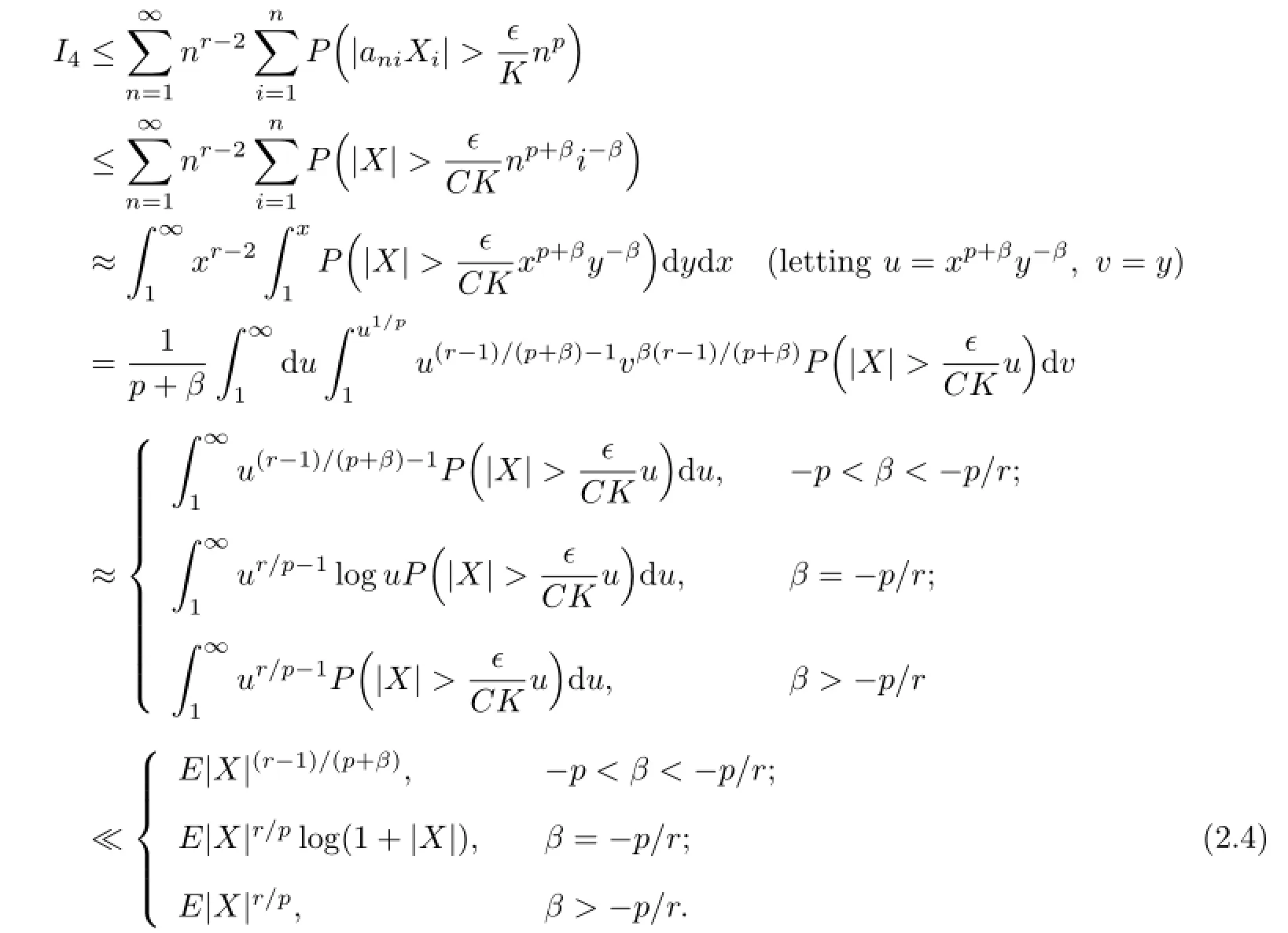
Therefore,by(2.1),I4<∞.From the defnition of,it is clear thatUsing Defnition 1.1,we deduce that
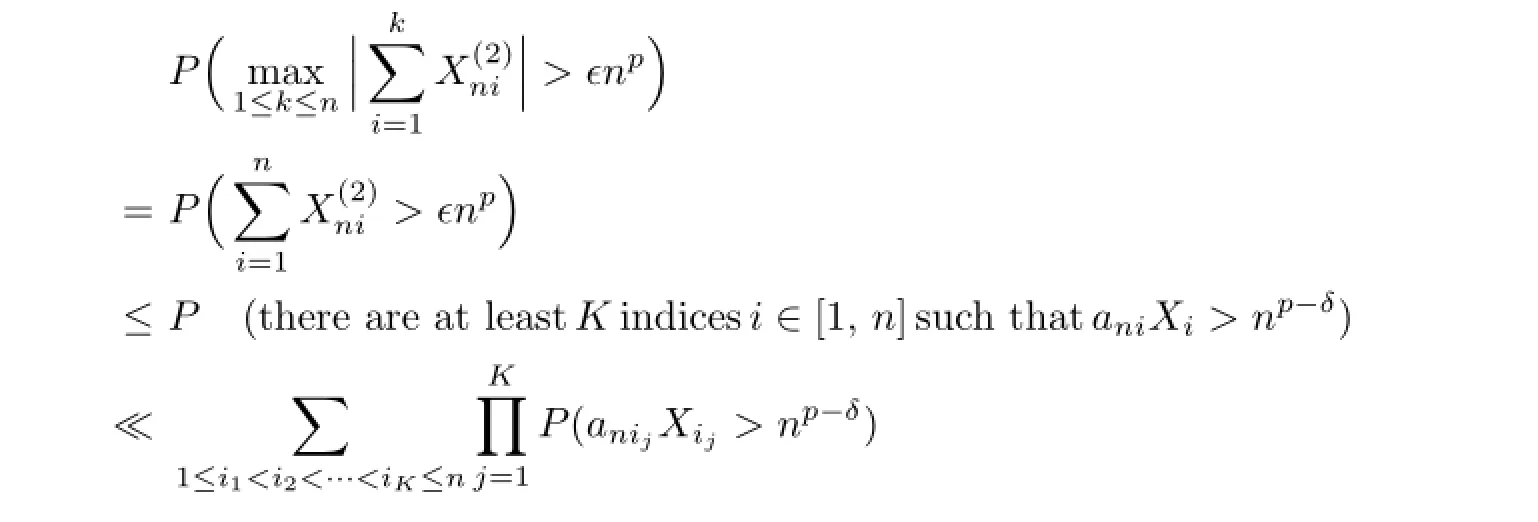

Since(2.1)impliesE|X|r Noting thatr>1,p+β>0,we can takeδsmall enough and take integerKsufciently large so that Thus,by(2.6)we getI2<∞.Similarly,we can showI3<∞.In order to estimateI1,we frst verify that Note that(2.1)impliesE|X|r we obtain by H¨older’s inequality that When 1/2<p≤1,noting thatEX=0,by choosing aδsmall so that we have Therefore,by(2.7)and(2.8),it sufces to prove that Taking a sufciently largetso that we have Whenr/p≥2,(2.1)impliesEX2<∞.Noting thatp+β>0,p>1/2,and choosing a sufciently largetso that we obtain Whenr/p<2,choosing a sufciently largetso that we have Thus,by(2.9)-(2.13),we have shown thatI1<∞.Therefore,(2.1)holds by(2.3)andIi<∞,i=1,2,3,4. Next,we proceed to prove that(2.2)implies(2.1).Since by(2.2),we have Therefore,by Lemma 1.4 and(2.15),we obtain Combining with(2.14)and(2.16),we deduce that From the proof of(2.4),it is obvious that(2.17)is equivalent to(2.1). Remark 2.1It is obvious that Theorem 1.2 of Liet al.[8]is a special case ofp=1,r=2 of Theorem 2.1 in this paper.Thus,we not only extend the result of Liet al.[8]for independent and identically distributed random variables to the case of sequences of extended negatively dependent random variables without necessarily imposing any extra conditions,but also the method used for proving Theorem 2.1 is diferent from that of Liet al.[8]. Remark 2.2Since negatively associated random variables are a special case of extended negatively dependent random variables,takingp=1 in Theorem 2.1,we obtain Theorem 1.3 of Liang[9].So Theorem 2.1 generalizes and improves the corresponding result of Liang[9]. Applying Theorem 2.1 withβ=0 andpreplaced by 1/p,we can get the following Baum-Katz type result for sequences of extended negatively dependent random variables as follows. Corollary 2.1Let{X,Xn,n≥1}be a sequence of identically distributed extended negatively dependent random variables,0<p<2and r>1.Then if and only if E|X|rp<∞,where EX=0whenever1≤p<2. [1]Liu L.Precise large deviations for dependent random variables with heavy tails.Statist.Prob. Lett.,2009,79:1290-1298. [2]Lehmann E L.Some concepts of dependence.Ann.Math.Statist.,1966,37:1137-1153. [3]Joag-Dev K,Proschan F.Negative association of random variables with applications.Ann. Statist.,1983,11:286-295. [4]Shen A T.Probability inequalities for END sequence and their applications.J.Inequal.Appl., 2011,2011:Article 98,12pp. [5]Chen Y Q,Chen A Y,Ng K W.The strong law of large numbers for extend negatively dependent random variables.J.Appl.Probab.,2010,47:908-922. [6]Hsu P L,Robbins H.Complete convergence and the law of large numbers.Proc.Nat.Acad. Sci.U.S.A.,1947,33:25-31. [7]Baum L E,Katz M.Convergence rates in the law of large numbers.Trans.Amer.Math.Soc., 1965,120:108-123. [8]Li D L,RAO M B,Jiang T F,Wang X C.Complete convergence and almost sure convergence of weighted sums of random variables.J.Theoret.Probab.,1995,8:49-76. [9]Liang H Y.Complete convergence for weighted sums of negatively associated random variables.Statist.Probab.Lett.,2000,48:317-325. [10]M´oricz F.Moment inequalities and the strong laws of large numbers.Z.f¨ur Wahrscheinlichkeitstheorie verw.Gebiete,1976,35:299-314. [11]Wu Q Y.Complete convergence for weighted sums of sequences of negatively dependent random variables.J.Probab.Statist.,2011,2011:Article ID 202015,16pp. A 1674-5647(2015)01-0040-11 10.13447/j.1674-5647.2015.01.05 Received date:May 21,2012. Foundation item:The NSF(11271020 and 11201004)of China,the NSF(10040606Q30 and 1208085MA11) of Anhui Province and the NSF(KJ2012ZD01)of Education Department of Anhui Province. * . E-mail address:liucunchao11@163.com(Liu C C),mlguo@mail.ahnu.edu.cn(Guo M L). 2010 MR subject classifcation:60F15,60E15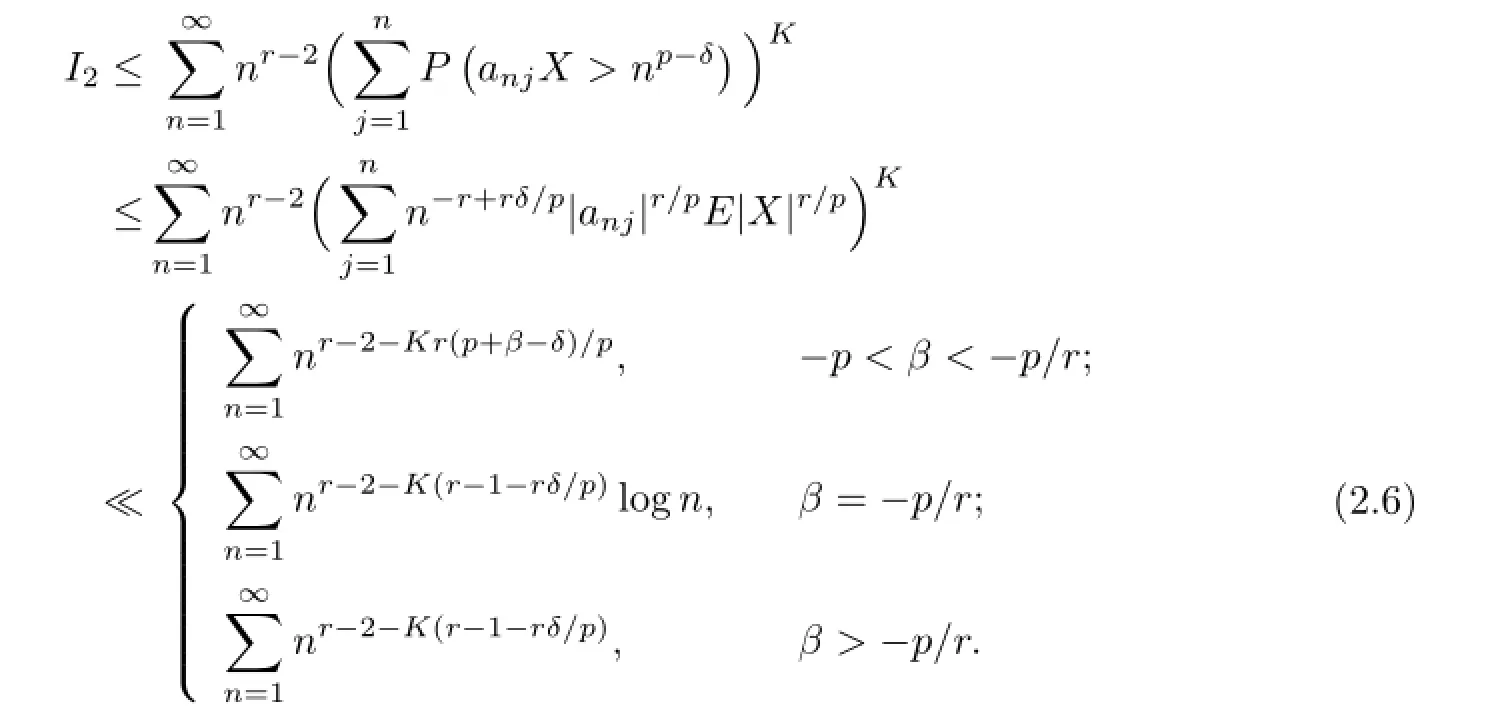
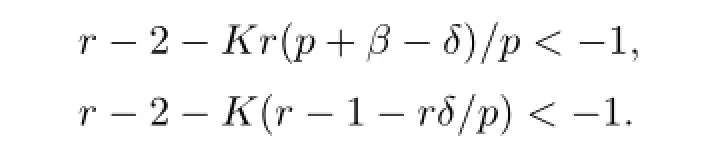

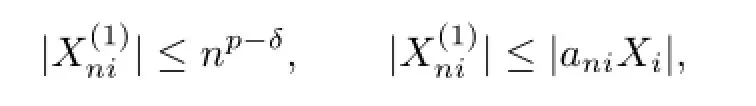
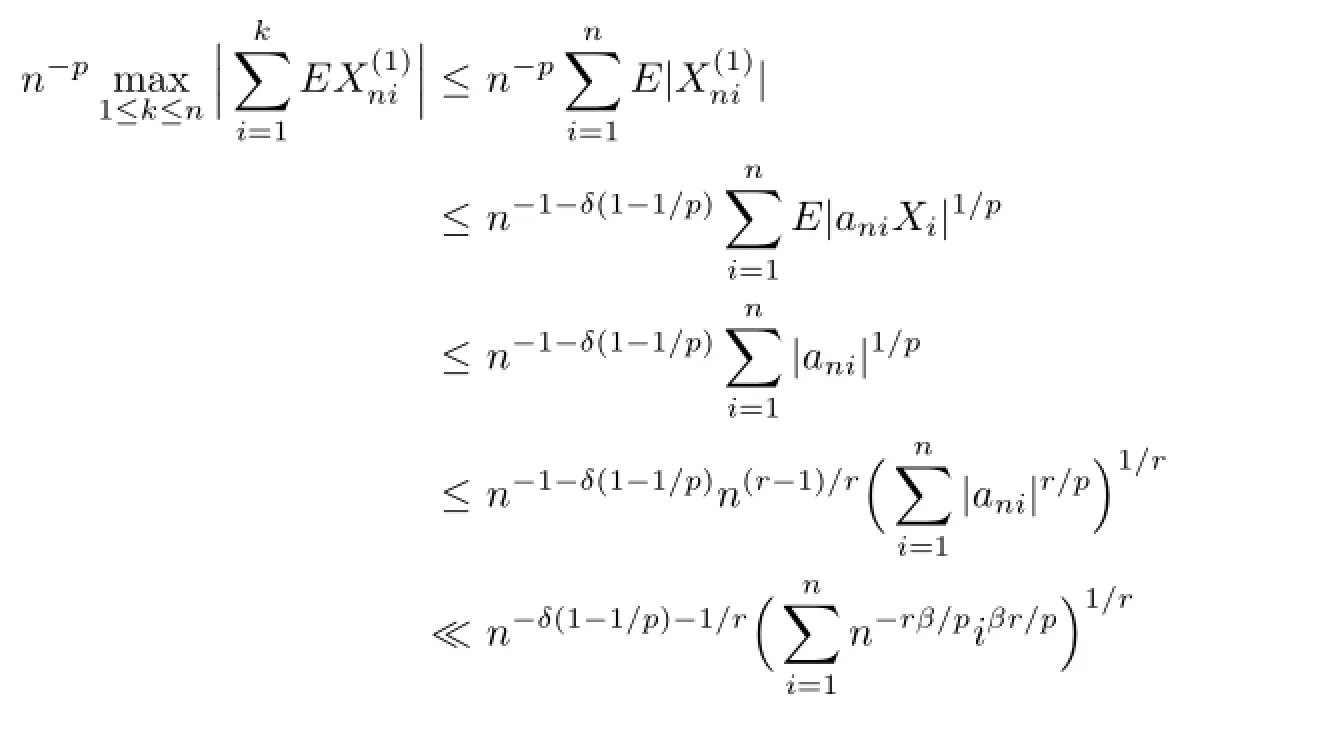
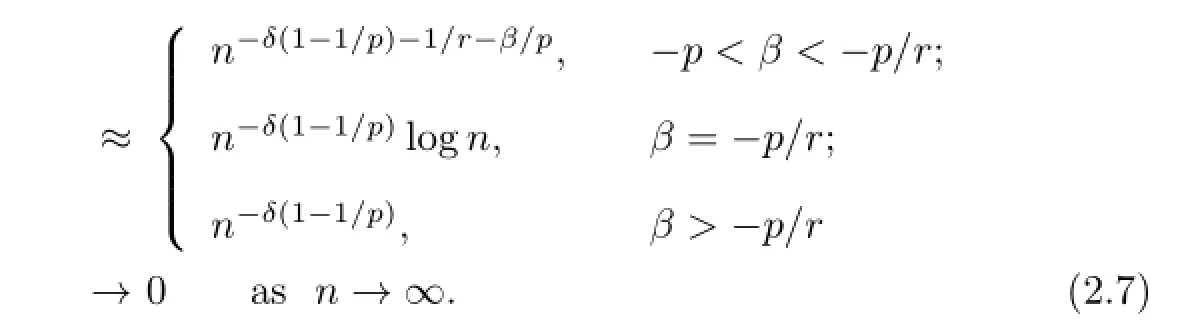

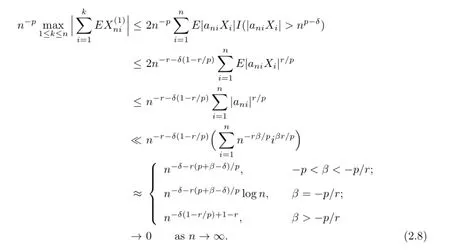
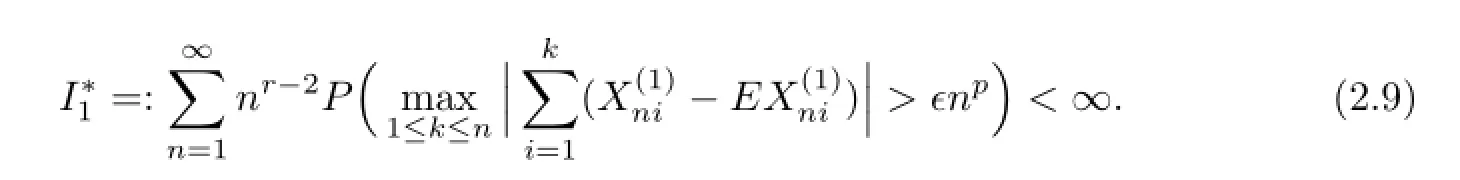
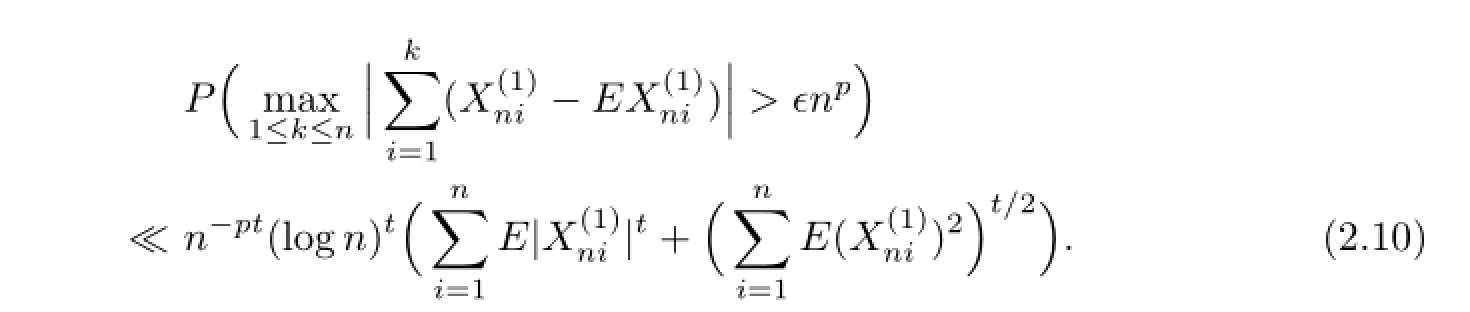
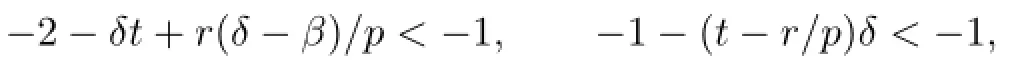
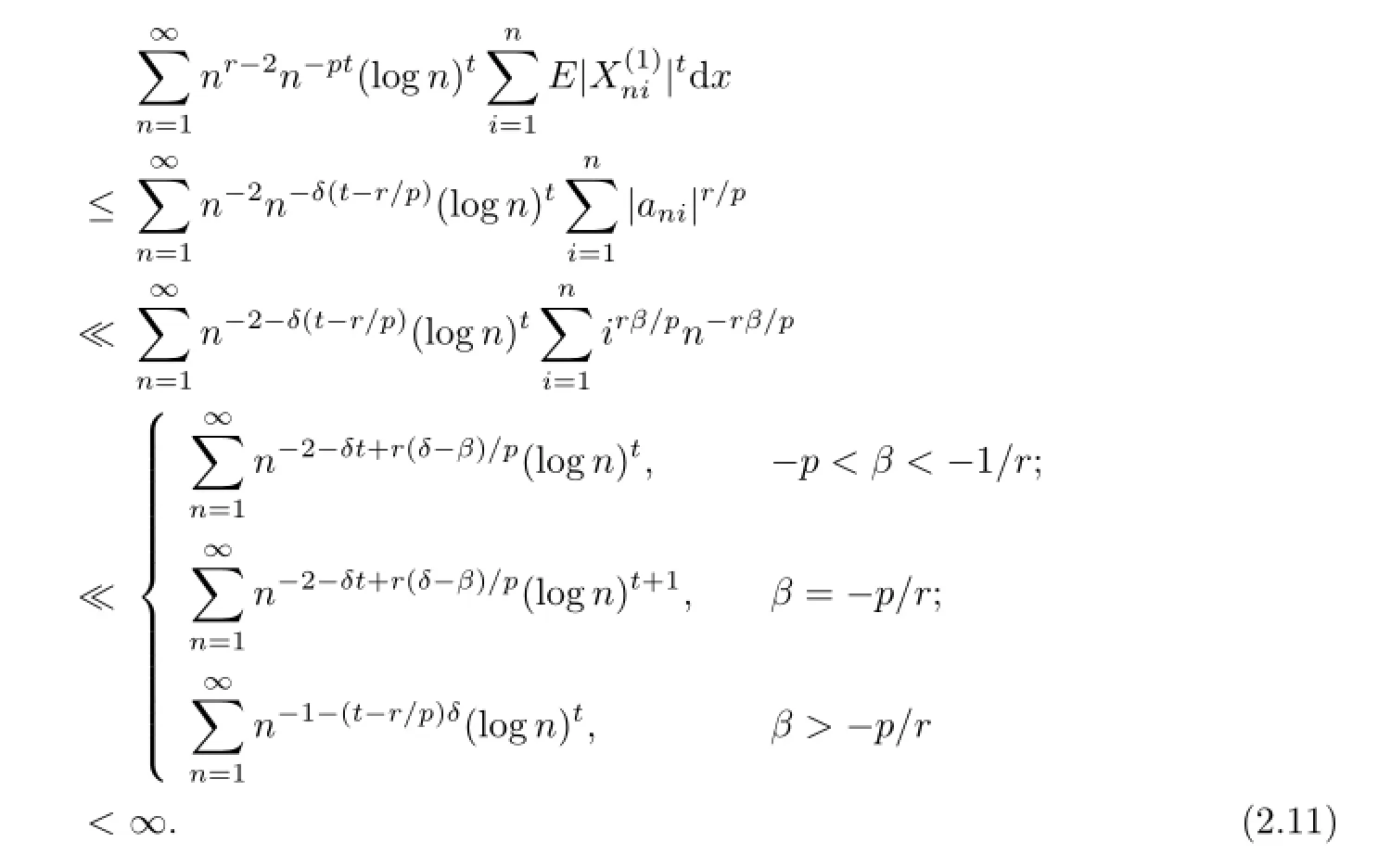
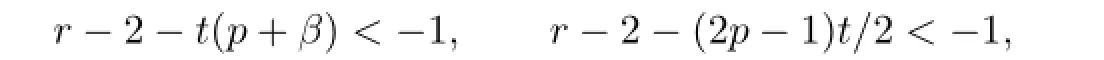
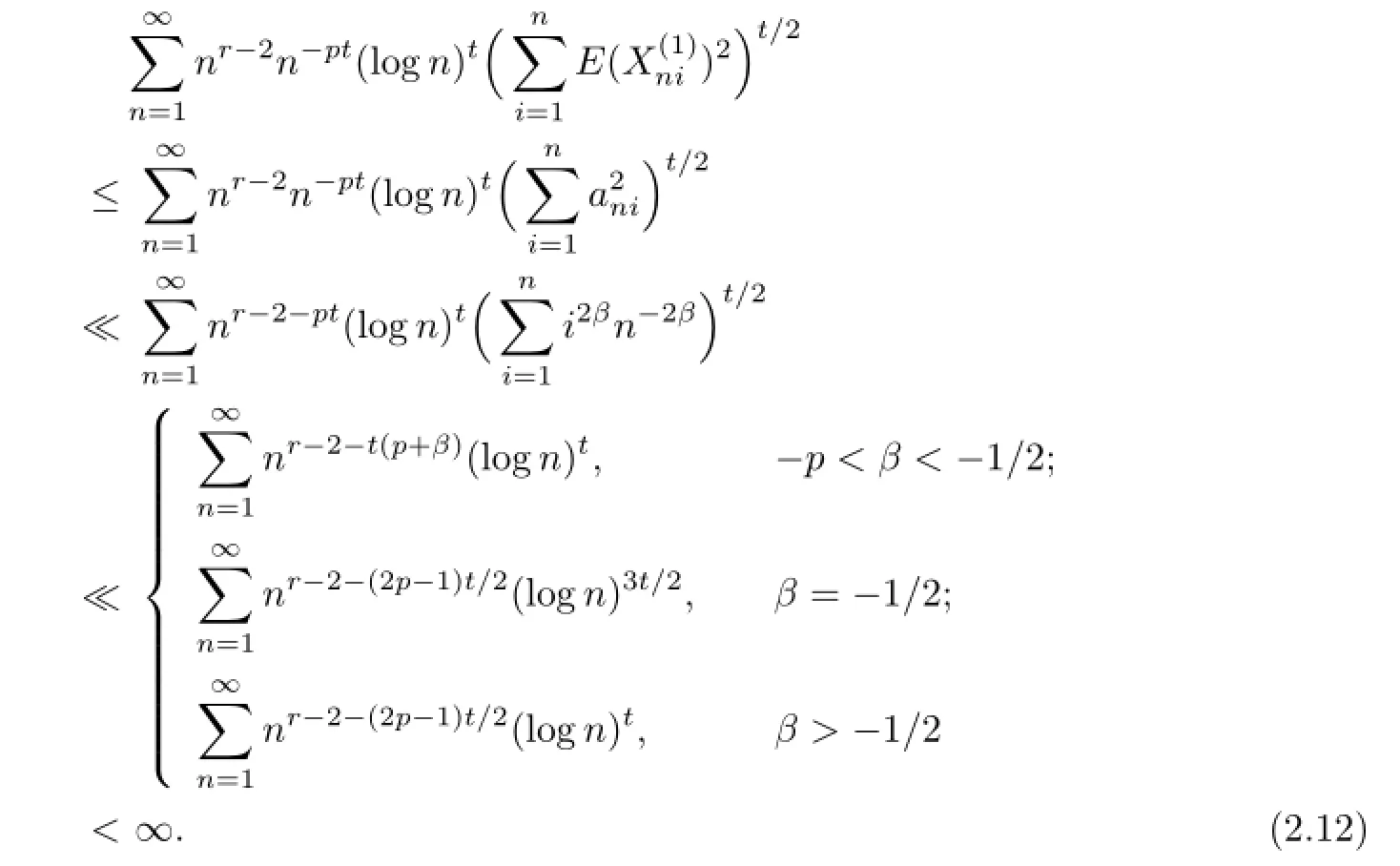
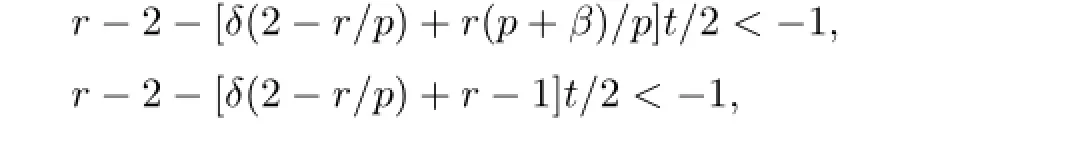
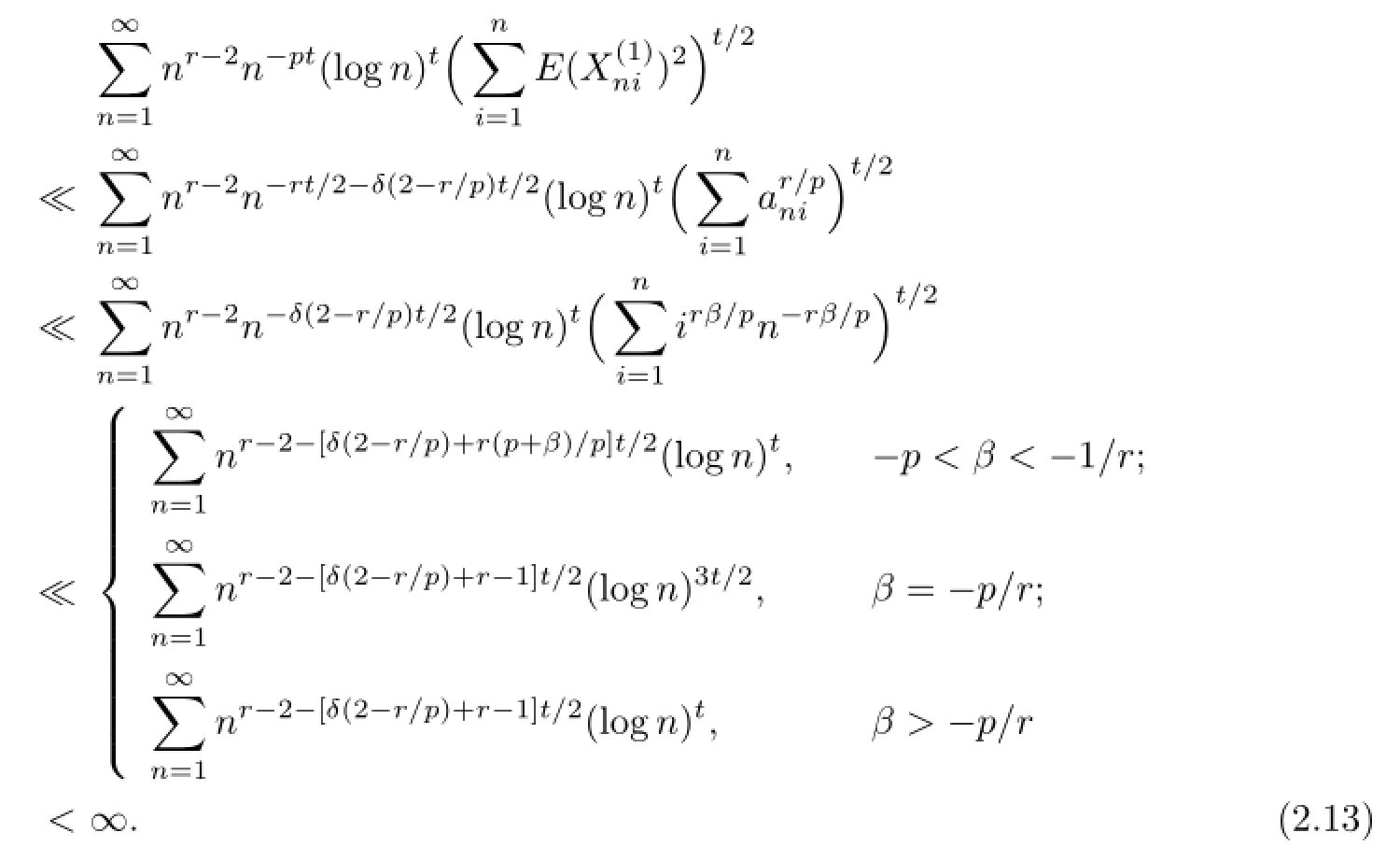
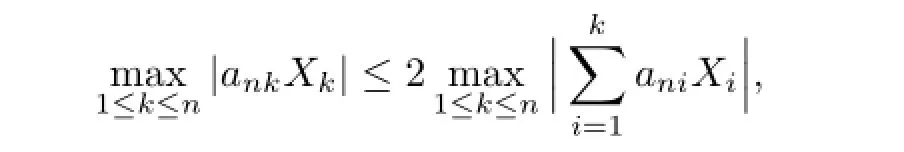
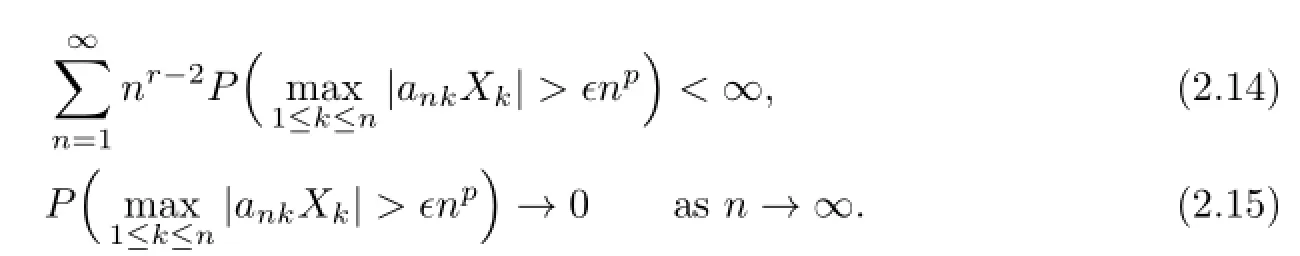

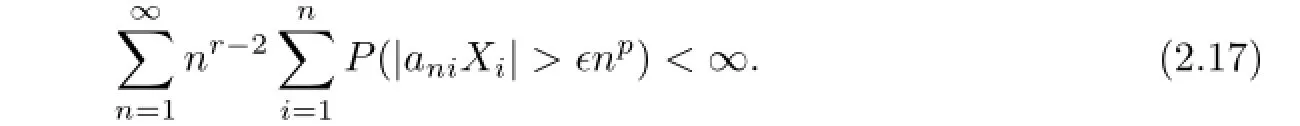
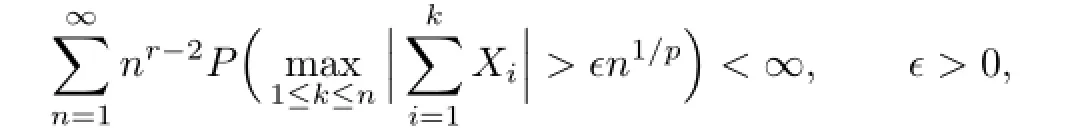
 Communications in Mathematical Research2015年1期
Communications in Mathematical Research2015年1期
