Derivative Estimates for the Solution of Hyperbolic Afne Sphere Equation

WU YA-DoNG

(College of Mathematics and Information Science,Jiangxi Normal University,Nanchang,330022)

Communicated by Rong Xiao-chun

Derivative Estimates for the Solution of Hyperbolic Afne Sphere Equation

WU YA-DoNG

(College of Mathematics and Information Science,Jiangxi Normal University,Nanchang,330022)

Communicated by Rong Xiao-chun

Considering the hyperbolic afne sphere equation in a smooth strictly convex bounded domain with zero boundary values,the sharp derivative estimates of any order for its convex solution are obtained.

hyperbolic afne sphere,Monge-Amp`ere equation,derivative estimate2010 MR subject classifcation:53A15,35J65

1 Introduction

In afne diferential geometry,the classifcation of complete hyperbolic afne hyperspheres has attracted the attention of many geometers.By a Legendre transformation,the classifcation of Euclidean-complete hyperbolic hyperspheres is reduced to the study of the following boundary value proble

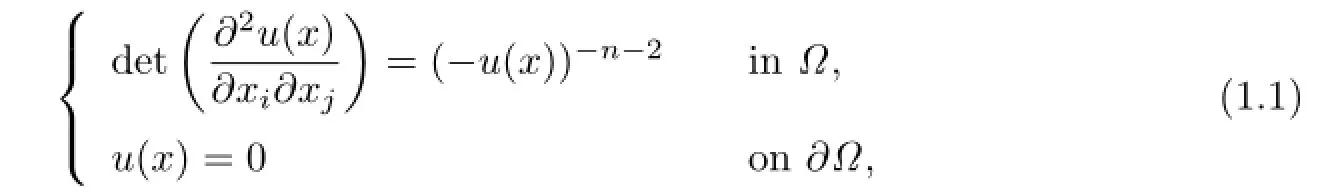
whereΩ⊂Rnis a bounded convex domain.Calabi[1]conjectured that there is a unique convex solution to(1.1).Loewner and Nirenberg[2]solved(1.1)in the cases of domains inR2with smooth boundary.Cheng and Yau[3]showed there always exists a convex solutionand the uniqueness follows from the maximum principal.

WhenΩ=Bn(1),the unit ball inRn,the convex solution of(1.1)is

WhenΩis projectively homogeneous,Sasaki[4]found that the convex solution of(1.1) and the characteristic functionχof domainΩhave the following relation:

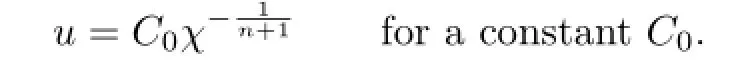
Also,Sasaki and Yagi[5]obtained an expansion of derivatives of the characteristic functionχalong the boundary of the smooth convex bounded domain.Referring the Feferman’s expansion of the Bergman kernel on smooth strictly pseudoconvex domains(see[6]),Sasaki[7]obtained an asymptotic expansion form ofχwith respect to the solutionu:

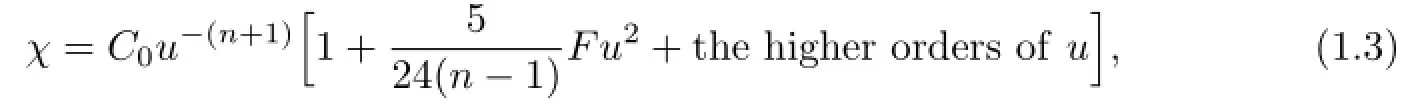
whereFis a smooth function on¯Ω.

In this paper,we confne ourselves to the case thatΩis a strictly convex bounded domain with smooth boundary.By the barrier functions on the balls,the convex solution of(1.1) has the bound:

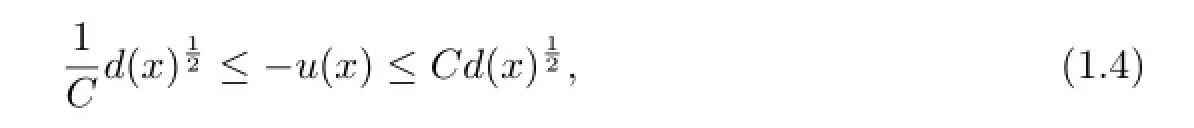
whered(x)=:dist(x,∂Ω),andCis a positive constant depending onΩandn.

By(1.4)and the convexity ofu,the gradient estimate is given by:

Loewner and Nirenberg[2]frst obtained the sharp second order estimates in dimension two.Their methods and Pogorelov’s calculations also gave bound for the higher dimensions (see[8]):

In this paper,by the fnite geometry of complete hyperbolic afne sphere as stated in Lemma 2.1,we obtain derivative estimates of any order:

Theorem 1.1For n=2,the convex solution of(1.1)satisfes

where C is a constant depending on Ω and|α|.

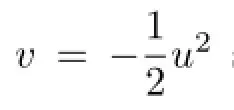
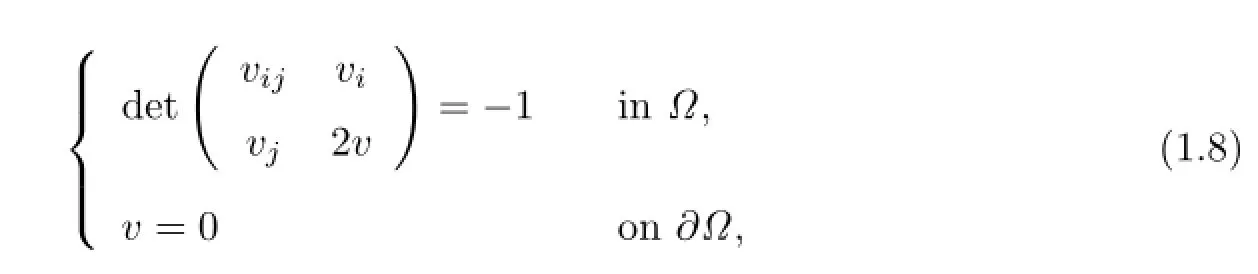
wherevi,vijare the usual frst and second derivatives.For the boundary behaviors of derivatives of the solutionu,it is necessary to study the smoothness ofvon the closure ofΩ,and to derive a complete description of the boundary singularity.

2 Formulas for Hyperbolic Afne Hyperspheres

LetMbe a locally strictly convex afne hypersurface inRn+1,given by a convex functionfdefned in a domainD⊂Rn:

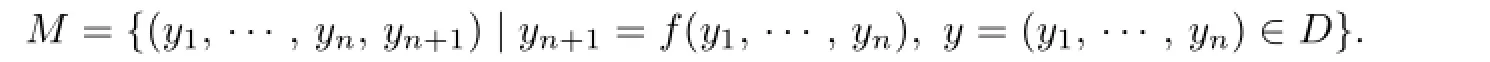
The Blaschke metric is given by(see[9])

wherefij(1≤i,j≤n)are the second derivatives offwith respect toy,(fij)is the inverse of matrix(fij),and

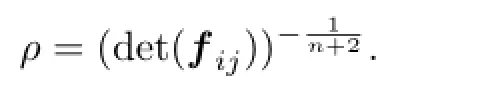
The Fubini-Pick form is given by(see[10])

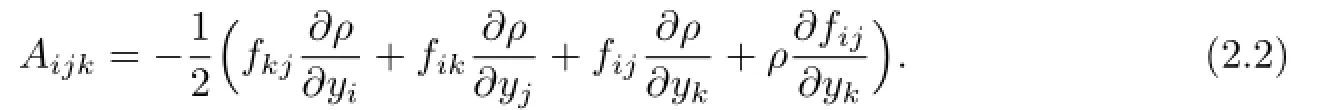
Consider the Legendre transformation relative tof

The Legendre transformation domainΩoffis defned by

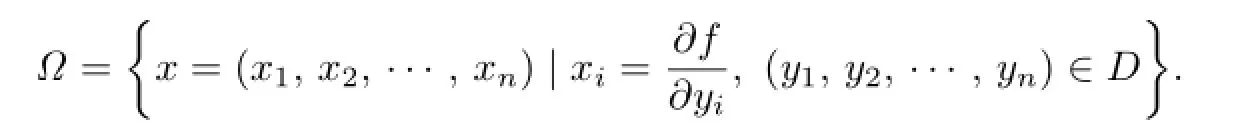
In the terms of coordinates(x1,x2,···,xn),the Blaschke metricGis given by

Here and later we denote byui,uij,uijk,···the derivatives ofuwith respect tox,(uij) the inverse of matrix(uij),and

By a direct calculation,the Fubini-Pick form can be represented in the following form:

Suppose thatM={(y,f(y))}is a hyperbolic afne hypersphere with center at the origin.Then the Legendre functionuoffsatisfes(see[11])

It follows from(2.4)that the Blaschke metric and the Fubini-Pick form are given respectively:

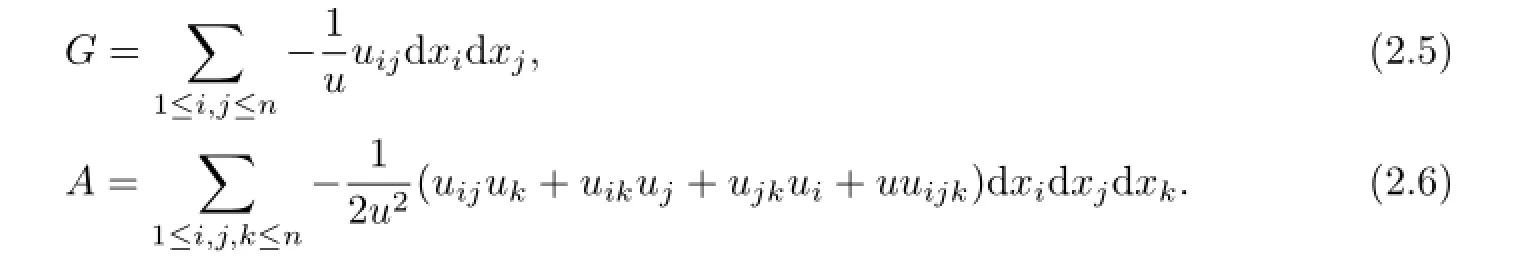
By using(2.4),the Laplacian with respect to the metricGis given by

There exist two notions of completeness on afne hypersurfaces inRn+1:(1)Euclidean completeness,that is the completeness of the Riemannian metric induced from a Euclidean metric onRn+1;(2)Afne completeness,that is the completeness of the Blaschke metricG.But for hyperbolic afne hyperspheres,these two completeness are equivalent(see[11]). Now we state a corollary of Theorem 2 of[9].

Lemma 2.1[9]Let M be a Euclidean-complete hyperbolic afne sphere inR3.Then M has fnite geometry:

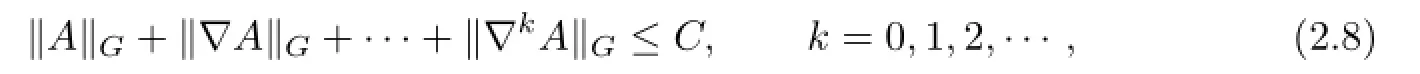
where C is a constant depending on k and∇is the covariant diferentiation with respect to the Blaschke metric G.

We remark here every Euclidean-complete hyperbolic afne hypersphere inRn+1has bounded Pick invariant‖A‖G(see[11]).Next,we give a Lemma due to Yau[12].

Lemma 2.2[12]Let(M,g)be a complete Riemannian manifold with Ricci curvature bounded from below.If a smooth positive function ϕ on M satisfes

where λ is a constant andΔis the Laplacian with respect to g,then there exists a constant C such that

3 The Third Order Derivative Estimates

In this section,we give the third order derivative estimates for any dimension.Letube the convex solution of boundary value problem(1.1)in a smooth strictly convex bounded domainΩ.Then the Blaschke metric

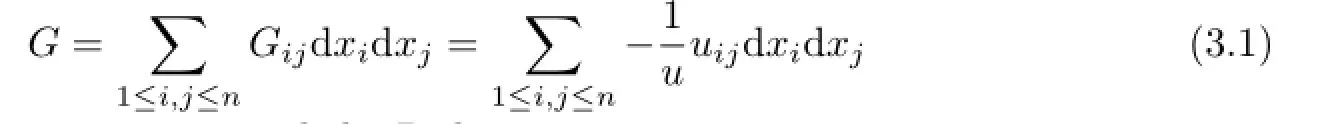
is a complete Riemannian metric,and the Pick invariant

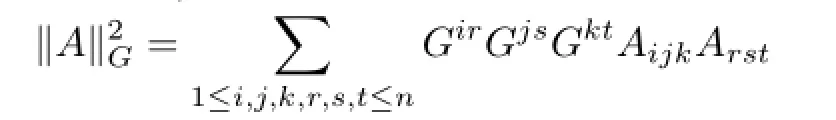
is bounded.For any pointx∈Ω,we assumeIt follows from(2.6)that

Here and later we use the sameCfor diferent constants.Diferentiating equation(1.1)with respect toxk,one has

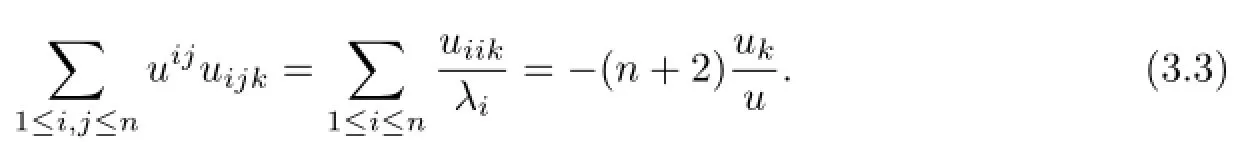
Inserting(3.3)into(3.2),we get

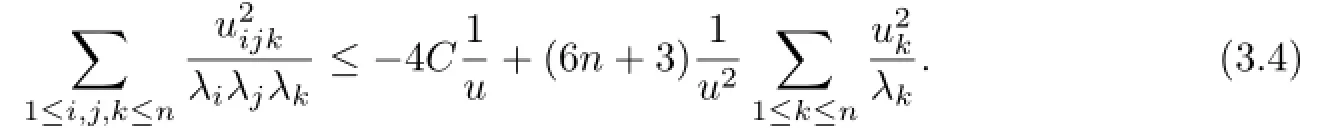
Combining(1.1)and(2.7),we have

Recall that the Ricci curvature of hyperbolic afne hypersphere is bounded from below(see [11]),by(3.5)and Lemma 2.2,we get

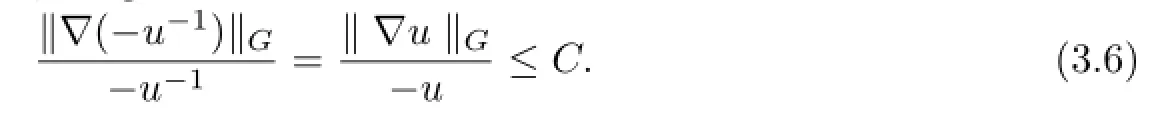
It follows that

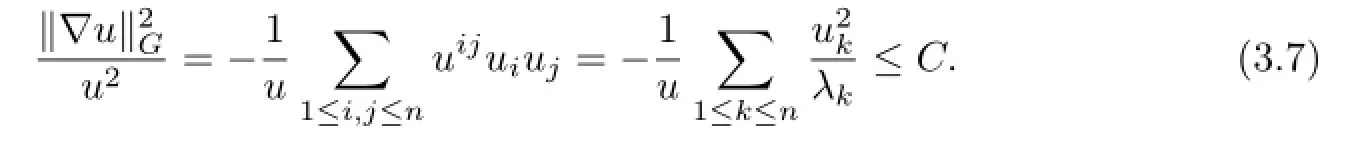
By using(1.4),(3.4)and(3.7),we have

Applying(1.6),we have proved

Formula(3.7)gives a lower bound of the maximal eigenvalue of Hessian(uij).In fact,

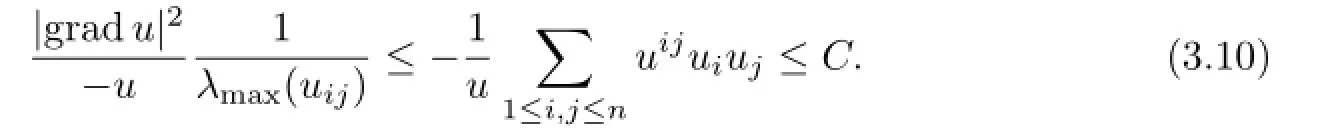
It follows from(1.4)and(1.5)that

Hence,by(1.6),we get

Corollary 3.1The convex solution of(1.1)satisfes

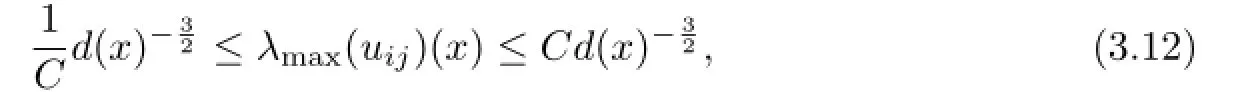
where C is a constant depending on Ω and n.

4 The Higher Order Derivative Estimates

In this section,we show(1.7)under the condition(2.8).Hence our theorem follows from Lemma 2.1.

Letube the convex solution of(1.1)in a smooth strictly convex bounded domainΩ,the Blaschke metric is given by(3.1).Then,by(2.6),the Christofel symbols ofGare given by

We write

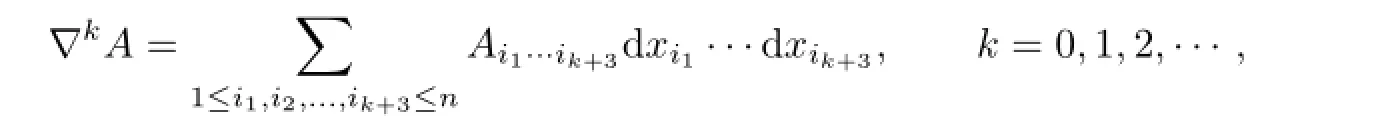
and assume that

To obtain(1.7),it sufces to prove the following estimates:

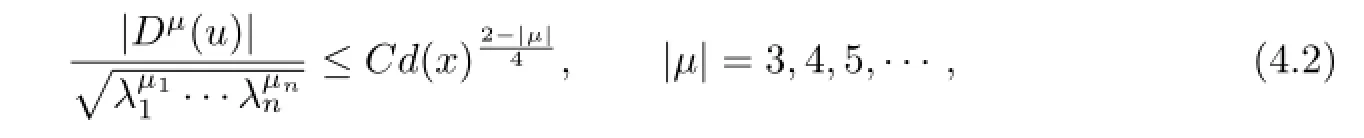
whereµ=(µ1,···,µn)andCis a constant depending onΩ,nand|µ|.

We proceed by introduction on|µ|.For|µ|=3,(4.2)is obtained in Section 3.Suppose that these estimates hold for|µ|≤m-1.To prove(4.2)for|µ|=m,we frst prove

Lemma 4.1For multi-index α=(α1,···,αn)with1≤|α|≤m-3,

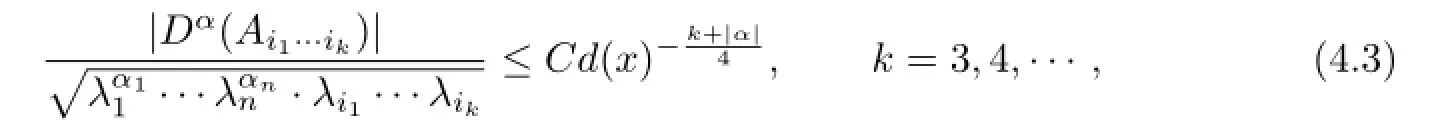
where C is a constant depending on Ω,n,k and m.

Proof.We proceed by introduction on|α|.Forα=(1,0,···,0),it is obvious that

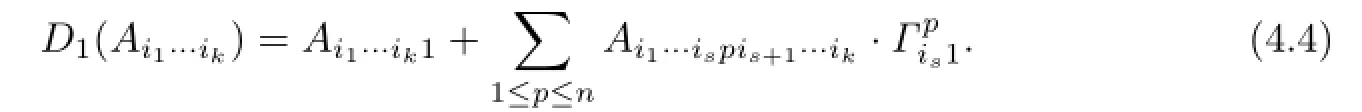
Noting that for any integrall＞0,‖∇lA‖Gis bounded,we have

Hence,by the estimate(1.4),we get

(4.1)gives

By(1.4)and(4.5)we have

From(1.4),(3.7)and(4.5)we also have

Combining the above estimates we have

This proves(4.3)for|α|=1.

Now suppose that the estimate(4.3)holds for multi-indexαwith|α|≤t.We need to prove that for|α|=t+1(4.3)holds.Without loss of generality,we assume thatDα=DβD1, whereβ=(β1,β2,···,βn)=(α1-1,α2,···,αn).Then

By using the Leibniz formula we have

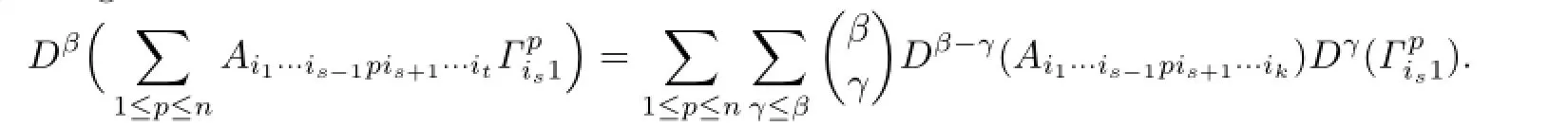
Noting the assumption that for|α|≤tthe estimate(4.3)holds,we have

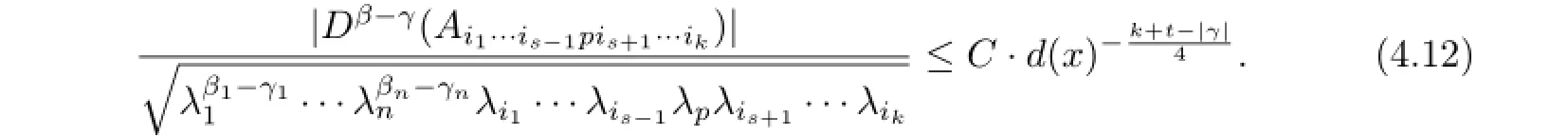
Applying(4.1)we have

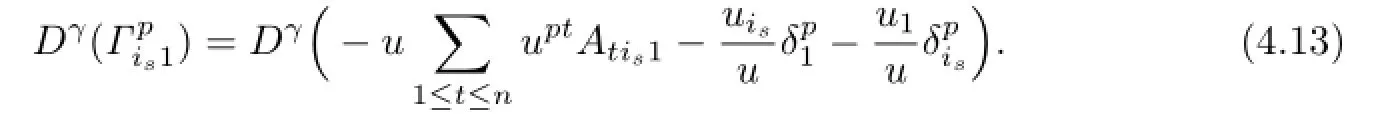
Noting that|γ|≤|β|=t≤m-3 and the assumption for|µ|≤m-1,we have

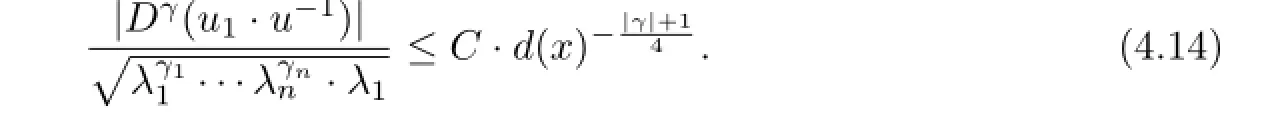
For multi-indexρ=(ρ1,···ρn)with|ρ|≤t≤m-3,the same reason gives

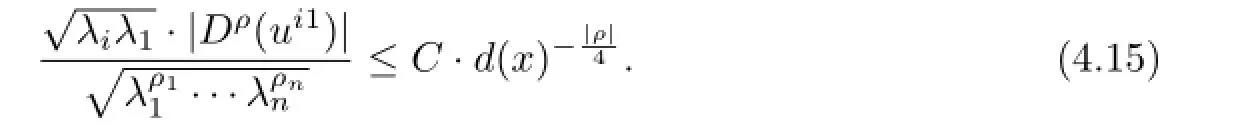
It follows from(4.15)and the assumptions for|α|≤tand|µ|≤m-1 that

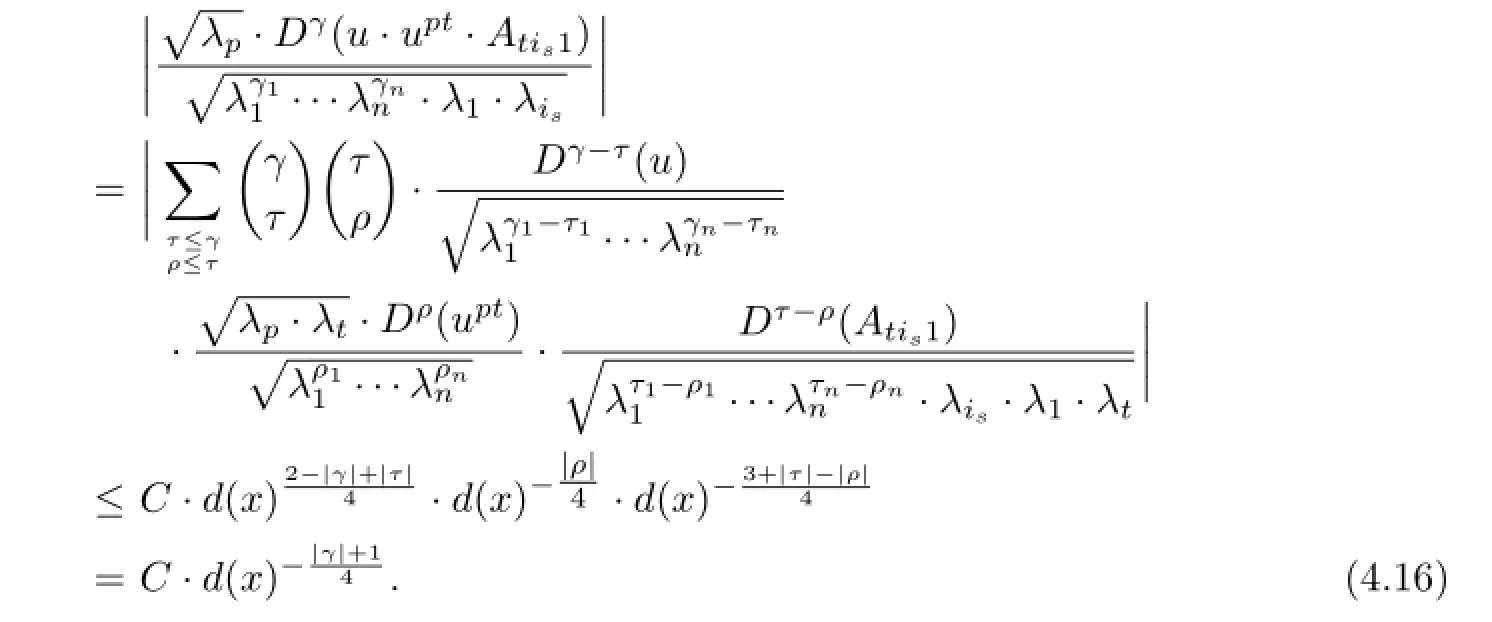
By the assumption for|α|≤twe have

Combining(4.11)-(4.14)and(4.16)-(4.17)we have

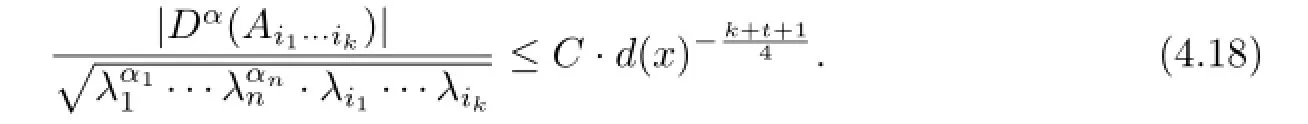
Now we prove that for|µ|=m(4.2)holds.By(4.3)we get

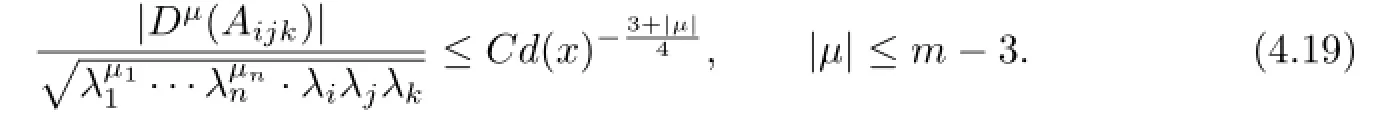
From(2.6),we get

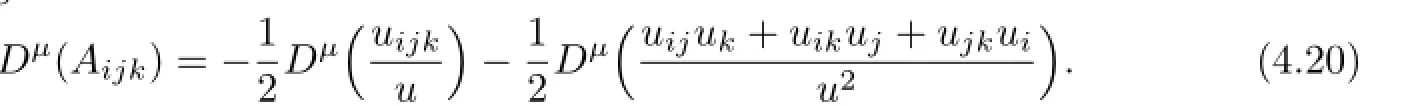
By using(1.4),(3.7)and the assumption for|µ|≤m-1,we have

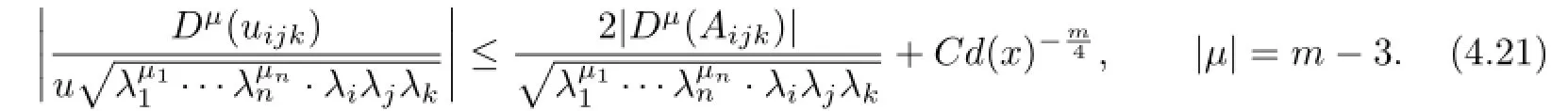
It follows from(1.4)and(4.19)that

This proves(4.2),furthermore,by using(1.6),we obtain(1.7).

[1]Calabi E.Complete afne hyperspheres I.Sympos.Math.,1972,10:19-38.

[2]Loewner C,Nirenberg L.Partial Diferential Equations Invariant Under Conformal Or Projective Transformations.in:Ahlfors L V,Kra I,Maskit B,Nirenberg L.Contributions to Analysis.New York:Academic Press,1974:245-272.

[4]Sasaki T.A note on characteristic functions and projectively invariant metrics on a bounded convex domain.Tokyo J.Math.,1985,8:49-79.

[5]Sasaki T,Yagi T.Sectional curvature of projective invariant metrics on a strictly convex domain.Tokyo J.Math.,1996,19:419-433.

[6]Feferman C.Parabolic invariant theory in complex analysis.Adv.Math.,1979,31:131-262.

[7]Sasaki T.On the characteristic function of a strictly convex domain and the Fubini-Pick invariant.Results Math.,1988,13(3):367-378.

[8]Wu Y D.Asymptotic behaviors of hyperbolic hypersurfaces with constant afne Gauss-Kronecker curvature.Results Math.,2011,59(1):173-183.

[9]Li A M,Jia F.Euclidean complete afne surfaces with constant afne mean curvature.Ann. Global Anal.Geom.,2003,23:283-304.

[10]Li A M,Zhao G S.Projective Blaschke manifolds.Acta Math.Sinica(English Ser.),2008,24(9):1433-1448.

[11]Li A M,Simon U,Zhao G S.Global Afne Diferetial Geometry of Hypersurfaces.Berlin: Walter de Gruyter,1993.

[12]Yau S T.Harmonic functions on complete Riemannian manifolds.Comm.Pure Appl.Math., 1975,28:201-228.

A

1674-5647(2015)01-0062-09

10.13447/j.1674-5647.2015.01.07

Received date:Jan.6,2013.

Foundation item:The NSF(11301231)of China.

E-mail address:wydmath@gmail.com(Wu Y D).