基于SDMR阻尼器的建筑结构半主动控制研究

于国军，孙 虎，苏 波，操礼林

(江苏大学土木工程与力学学院，江苏镇江 212013)

基于SDMR阻尼器的建筑结构半主动控制研究

于国军，孙 虎，苏 波，操礼林

(江苏大学土木工程与力学学院，江苏镇江 212013)

基于SDMR阻尼器对建筑结构非线性振动进行了半主动控制研究。引入Bouc-Wen模型来反映某建筑结构的非线性特征，采用基于能量的振动主动控制策略来确定结构控制力的大小，采用改进的遗传算法对SDMR阻尼器在结构中的布置位置进行优化，之后进行了结构半主动控制仿真研究。研究结果表明:SDMR阻尼器不仅对建筑结构在遭遇多遇地震(结构发生线性振动)时可实现有效控制，而且建筑结构在遭遇罕遇地震(结构发生非线性振动)时也可实现有效控制，其阻尼力和可调倍数比只针对多遇地震(结构发生线性振动)的常规阻尼器具有更好的适应性，并能提供足够的阻尼力储备。

SDMR阻尼器;半主动控制;改进的遗传算法;地震

在强烈地震尤其是罕遇地震的作用下，建筑结构往往发生非线性的塑性变形。针对建筑结构非线性地震响应的振动控制问题，国内外大多采用常规MR阻尼器进行振动控制［1-2］，而常规MR阻尼器往往是以线性振动结构为控制对象进行设计的，对于非线性较弱的情况减振效果明显。然而，大量的实际结构往往存在较强的非线性［3］。针对这个问题，本文采用SDMR阻尼器对建筑结构进行振动控制研究。首先，引入Bouc-Wen模型［4］来反映建筑结构的非线性特征，采用基于能量的振动主动控制策略来确定结构控制力的大小;然后，采用改进的遗传算法［5］解决建筑结构半主动控制中阻尼器的优化布置问题;最后，以某8层建筑物为工程案例，进行了基于SDMR阻尼器的结构半主动控制仿真研究。

1 SDMR阻尼器

自解耦式磁流变(self-dcoupling magneto-rheological，SDMR)阻尼器［6-7］是一种用于土木工程结构抗震(振)的阻尼器，具有阻尼力解耦特性和失效自保护功能，如图1所示。它对激励频率和振幅都很敏感，在不同的频率和振幅下具有截然不同的刚度和阻尼特性，并且可以有效降低各种地震激励下的结构反应，具有良好的稳定性和安全失效机制。其工作核心是主活塞(1)和2个副活塞(2)，在工作缸中充有磁流变液(3)，在主活塞上布置永磁体(4)和励磁线圈(5)，在副活塞导磁体中间设有永磁体和自解耦挡板(6)。在主活塞与缸体之间的阻尼通道中的磁场由永磁体和励磁线圈共同作用产生;在副活塞与缸体之间的阻尼通道中磁场则由永磁体单独产生。该阻尼器结构如图2所示，其主要性能设计参数如表1所示。

图1 SDMR阻尼器实物

图2 SDMR阻尼器结构

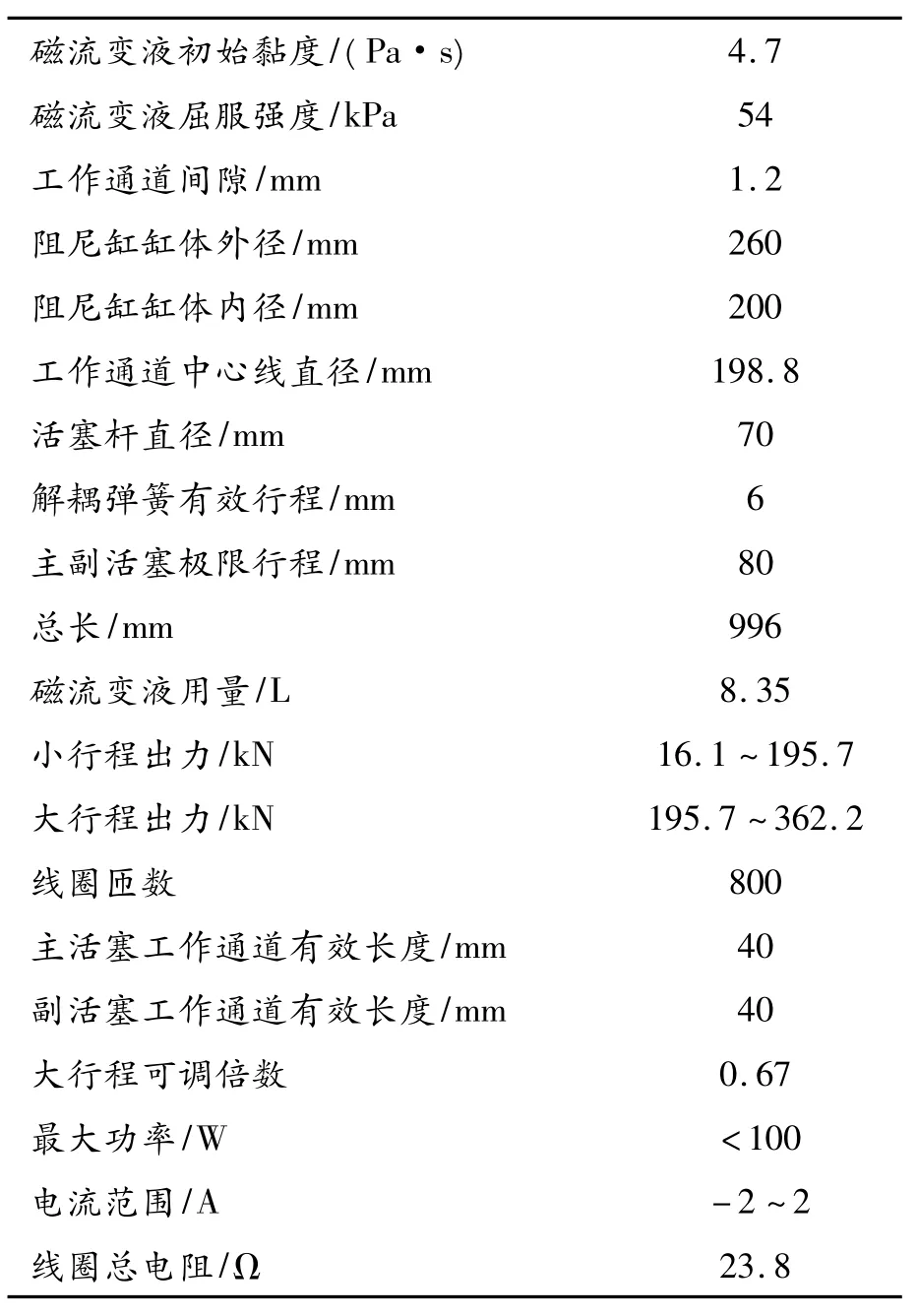
表1 SDMR阻尼器的主要性能设计参数

2 建筑结构非线性振动的半主动控制策略

2.1 非线性结构系统的运动方程

安装m个MR阻尼器的n自由度结构在单向水平地震加速度作用下的运动微分方程可表示为

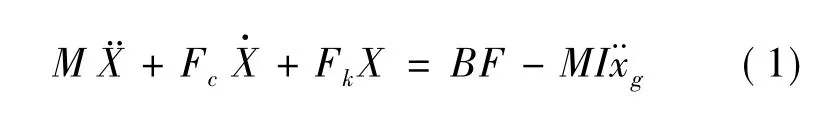
式中:M为结构的质量矩阵;和X¨分别为结构的位移、速度和加速度响应;FkX是非线性结构的刚度恢复力;是非线性结构的阻尼力;F= -MI是将各时刻的地震外激励施加于各集中质量;B是布置MR阻尼器的位置矩阵;I是由1组成的列向量;F是由MR阻尼器产生的控制力。

基于可描述材料非线性的Bouc-Wen模型［8］，假设为黏性阻尼力，则有:

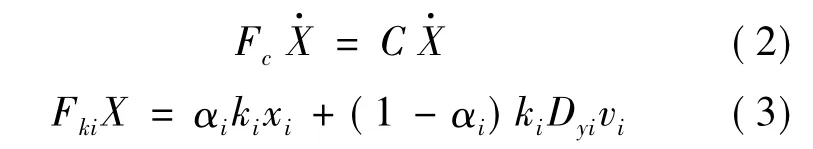
式中:FkiX为FkX的第i个分量;ki为结构第i层的弹性刚度;C为n×n的阻尼矩阵;αi为结构第i层的屈服后刚度与屈服前刚度之比;yi=xi-xi-1为结构的层间位移;Dyi为结构第i单元层的极限屈服位移，若结构形式已确定，对于结构的第i个单元层而言Dyi为一个已知常数;vi为表征结构滞回性能的无量纲参数，要求

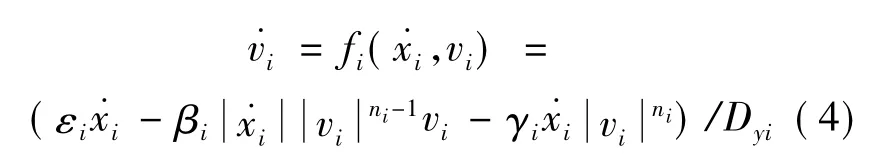
式中:εi，βi，γi和ni为表征结构第i单元层的非弹性滞回部分的常参数;εi为恢复力幅值常数，一般取1;βi和γi为控制恢复力曲线的形状的常数;ni为控制恢复力曲线光滑的常数。本文对这些参数的确定采用“三阶段识别方法”［9］。

将式(2)、(3)代入式(1)，则用层间位移表示的振动方程为

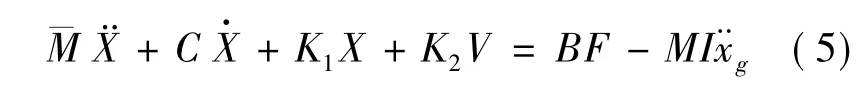
将式(5)变换为状态方程:

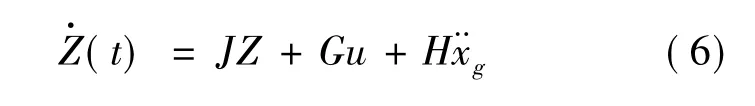
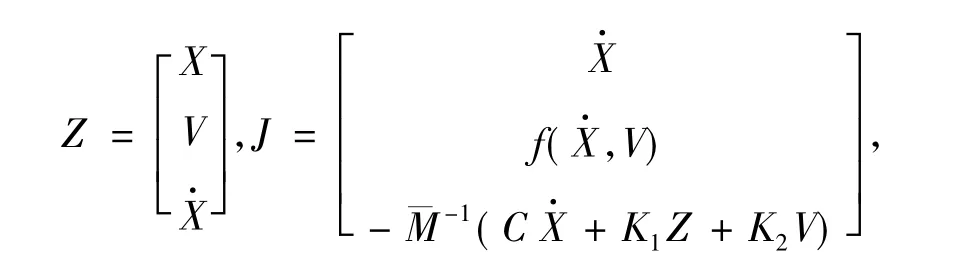
式中:满足下式:

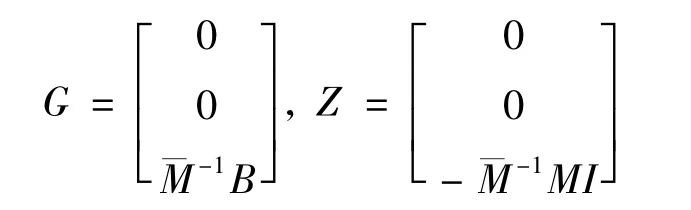
2.2 非线性结构的控制算法

对于非线性结构振动控制中控制力的确定，可先根据建筑楼层的允许位移和速度计算出结构的允许能量;根据结构在地震作用下实际发生的位移和速度计算出结构的实际能量;然后将允许能量与实际能量进行比较并确定控制力的大小［10］。

结构在地震作用下能量的分布服从Rayleigh概率分布，其密度函数可表示为:

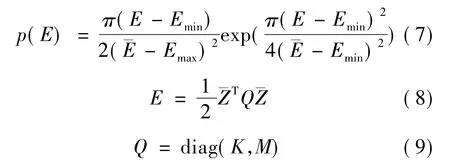
式中:Emin为结构的最小能量;为平均能量分别为结构的刚度和质量矩阵。

为确定结构振动控制中控制力的大小，如果采用积分或数值解法，均不易实施。因为对于非线性振动，积分不易实现，而数值解法计算时间长，不利于实时控制。因此，本文基于一种线性控制策略实现控制力的计算。

式(7)、(8)不变，将式(9)修改为:

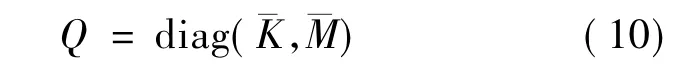
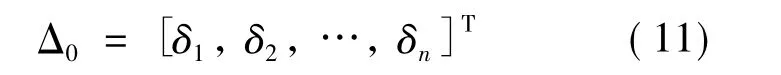
则被控结构的允许能量为

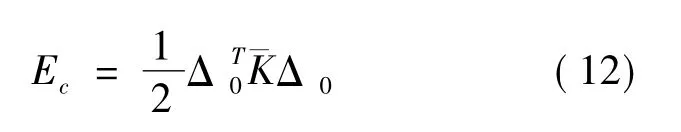
2．3 半主动控制策略

将t时刻测量的位移信号代入式(8)，令质量矩阵为零，可得结构实际振动能量，设其为Et。结合SDMR阻尼器，输出力采用阶跃函数，即在计算下一步控制力时当前控制力保持不变。因此，第j个阻尼器的控制力为

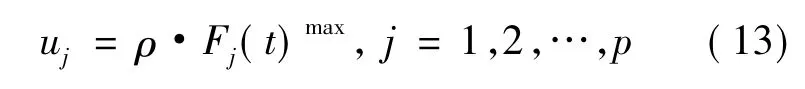
式中:Fj(t)max为第j个阻尼器所允许的最大控制力，SDMR阻尼器的阻尼力Fj(t)max由所识别出的阻尼力确定［6］;ρ的表达式为

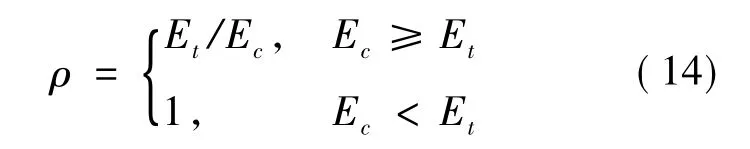
对于式(13)中控制力的方向可依据Lyapunov控制器的设计概念来确定［11］，定义为

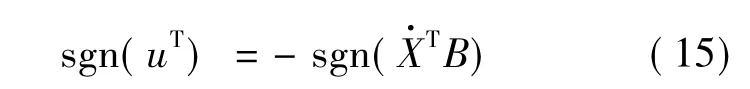
式中sgn(·)为符号函数。

由式(13)、(14)可知:当测量出的被控结构实际振动能量比计算出的允许能量小或相等时，所需控制力小于或等于阻尼器的容量限;当测量出的被控结构实际振动能量比允许能量大时，控制力取阻尼器的最大控制力。

3 SDMR阻尼器在建筑中的优化布置

建筑结构半主动振动控制系统的振动控制效果不仅取决于控制算法的优劣，也取决于控制装置在建筑结构中的布置位置。在建筑结构中布置较多的阻尼器一般可以达到较好的控制效果。但是如果在建筑结构的每层中都设置SDMR阻尼器，一方面会因阻尼器的数量庞大而降低振动控制效率和控制系统的可靠性，另一方面由于阻尼器数量增多需要同时匹配相应的测试及控制系统，这无疑会提高建筑成本。因此，对SDMR阻尼器的布置位置进行优化对于建筑结构的振动控制具有重要意义。

3.1 建筑结构中SDMR阻尼器的优化布置准则

目前常用的优化布置准则主要包括:对结构振动能量的耗能最大化原则;基于舒适性和安全性而确立的迭代法准则;基于二次型性能指标灵敏度的优化准则;以振型为控制目标函数的振型法准则等。本文依据《建筑抗震设计规范》(GB50011—2010)中的结构抗震变形验算原则进行安全性优化布置，即依据结构在遭遇地震作用时，结构的层间位移角最大值是否小于限定值作为结构发生弹性或弹塑性变形的判断标准。因此，以建筑结构的最大层间位移角和半主动控制实现的加速度指标达到最小值为目标。该最优布置问题的目标函数为

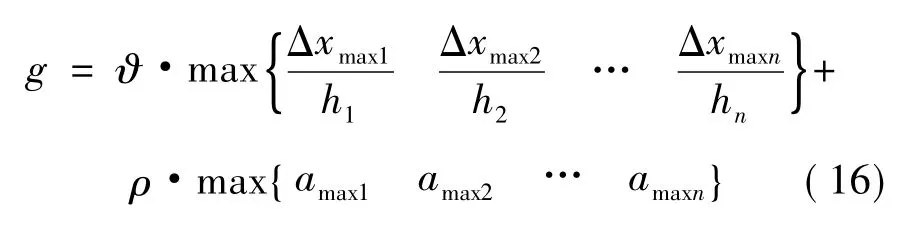
式中:Δxmaxi和amaxi分别为结构的第i层发生的最大层间相对位移和最大加速度;hi为第i楼层的层高;g为结构所有楼层中最大的相对层间位移角;ϑ和ρ分别为考虑安全性和经济性的加权系数。

建筑结构中SDMR阻尼器的优化布置要求g达到最小，故采用以下适应度函数:

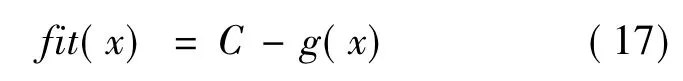
式中C是一个常数，大于群体中g(x)的最大值。

3．2 改进遗传算法的设计

遗传算法是模拟生物在自然环境中遗传和进化过程的一种自适应优化概率的搜索方法。目前，遗传算法已发展出诸如混合遗传算法、多种群遗传算法、微种群遗传算法等修正形式。但这些方法在处理建筑结构中阻尼器位置优化问题时，往往会在繁殖产生新个体时违背约束条件，导致算法难以求解，即使采用罚函数进行约束条件的处理，也不能保证不出现违背约束条件的新子代个体［13-20］。为此，采用改进的遗传算法处理建筑结构中阻尼器的位置优化问题。

1)编码

假设有m个MR阻尼器，有n个可布置阻尼器的建筑结构位置，阻尼力位置矩阵B中的第k个列向量为:其中，第i行的1表示在结构的第i层上布置第k个MR阻尼器;如果第i行值为0，表示在结构的第i层上不布置MR阻尼器。这样Ek就由二进制编码表示。如:假设n=10，则编码0100110010表示在位置2，5，6和9位置上布置MR阻尼器。若用ti表示第i个码位上的基因值，则约束条件可表示为

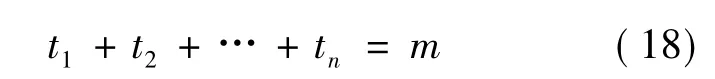
2)建立初始种群

针对上述的约束条件，在个体两两不同和尽可能保持初始种群的多样性这2个生成原则下随机生成二进制编码串，并建立初始种群。

3)选择

选择是从种群中选出作为可繁殖产生新个体的父代个体。在式(17)适应度函数的基础上采用两两联赛法进行选择。其方法是:首先从种群中选出2个父代个体，通过适应度计算，将适应度小的父代个体淘汰，保留适应度大的父代个体。

4)交叉

交叉是将2个父代编码串进行替换重组的操作，在遗传算法中起核心作用。由于所针对的建筑结构振动控制中安装MR阻尼器的数目是确定的，这个约束条件在传统的交叉操作中往往会被破坏，因此采用改进的交叉方法来产生子代。具体方法:随机产生一个二进制串，串长与个体长度相等。对于二进制串为1的基因位，让父代个体基因进行交叉置换;对于二进制串为0的基因位，让父代个体基因保留。要求所采用的交叉码使父代基因值满足式(18)的约束。改进的交叉操作见图3。

图3 改进的交叉操作示意图

5)变异

变异操作可采用交换子代中的任意2个基因的变异方法。这样仍满足约束条件且不会破坏对阻尼器总数的约束。

3.3 改进遗传算法的实现步骤

经过以上改进遗传算法的设计，其算法实现流程如图4所示。

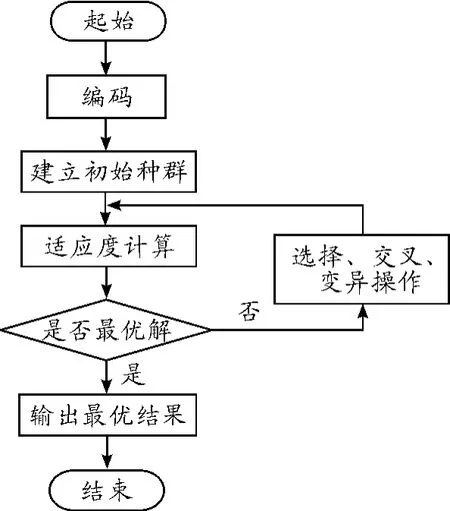
图4 改进遗传算法流程

4 基于SDMR阻尼器的建筑结构半主动控制仿真

4.1 建筑结构模型

建筑结构模型来源于某技术培训楼。该建筑为7层钢筋混凝土框架结构。底层和顶层层高3.3 m，其他层层高均为3 m，抗震设防烈度为8度。结构的柱网布置平面及框架剖面如图5所示。

图5 建筑结构布置图

在确定结构体系的计算模型时作如下假定:建筑结构的质量全部集中在建筑的楼板层和屋面层;建筑结构为剪切型，遭遇地震时结构的变形表现为层间侧移;楼板和屋面在结构平面内刚度无穷大，且同一结构层的侧移量相同。

4.2 建筑阻尼器位置优化的实现

根据《建筑抗震设计规范》(GB50011—2010)，在地震烈度为8度时，多遇地震、设防地震、罕遇地震的加速度峰值分别为0．070g，0．200g和0．400g。截取El-Centro地震波的一部分(20 s的时程曲线)，并将加速度峰值分别按多遇地震、设防地震、罕遇地震的加速度峰值进行调整。

针对上述钢筋混凝土结构模型，选用多遇地震对应的加速度时程作为地震激励。每层结构模型中最多设置1个SDMR阻尼器，共设置3个，采用式(13)的控制策略。基于改进遗传算法在Mat-lab软件中编制SDMR阻尼器的位置优化程序，得出的优化结果为:(1 1 0 0 0 0 1)。为比较优化布置的优势，对混凝土结构模型进行了一次随机任意布置的仿真分析，其布置方式为:(0 1 0 0 0 1 1) (括号中的数字1为该楼层布置一个SDMR阻尼器，数字0为该楼层不布置SDMR阻尼器)。仿真计算结果如表2所示。

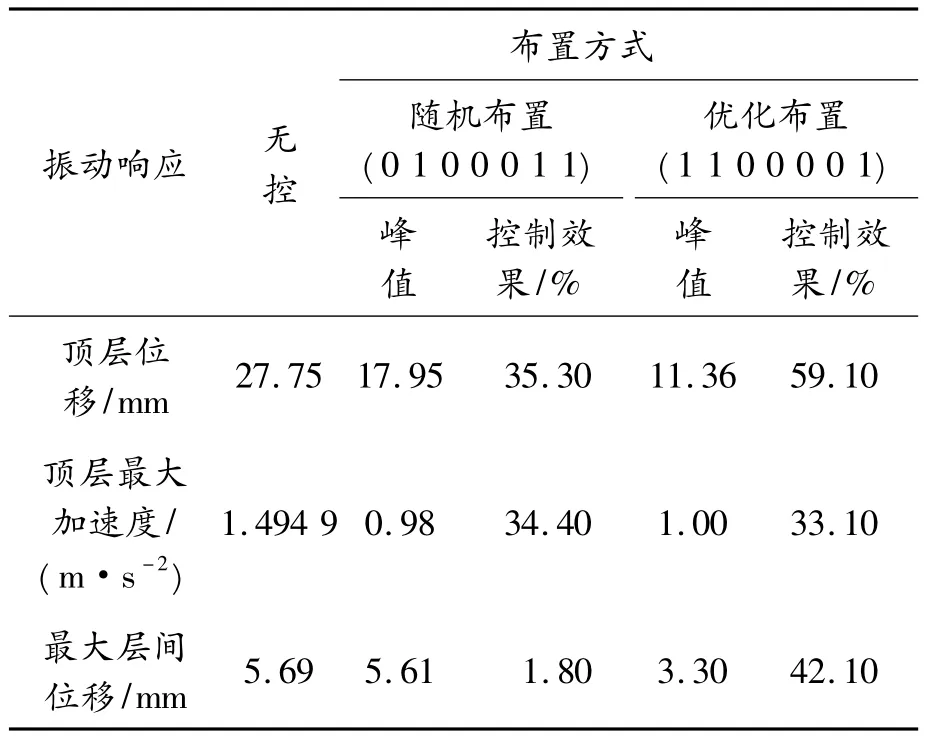
表2 结构在不同阻尼器布置方式下的振动控制效果

由表2可以看出:利用SDMR阻尼器来减小建筑结构的地震响应是非常有效的;阻尼器的布置位置对控制效果有着非常重要的影响。布置位置经过优化处理后，建筑结构的顶层位移、顶层最大加速度和最大层间位移的振动控制效果比SDMR阻尼器随机布置的控制效果好很多。

4.3 建筑结构半主动控制的仿真

采用上述SDMR阻尼器在结构中的优化布置方式，对多遇地震(0．07g)、设防地震(0．20g)和罕遇地震(0．40g)作用下的建筑结构分别采用未加控制装置(无控)、SDMR阻尼器被动控制(阻尼器无外部输入电流)和SDMR阻尼器半主动控制3种方式进行仿真分析。3种激励下的结构的顶层位移和加速度响应、各层最大加速度和侧移角响应分别如图6～8所示。振动响应最大值如表3所示。

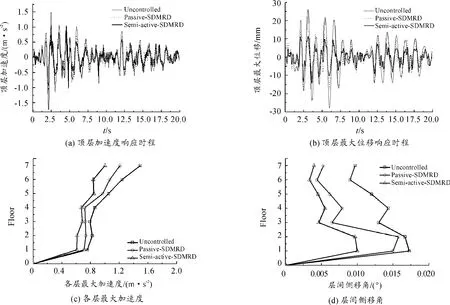
图6 多遇地震(0．07g)时的地震响应

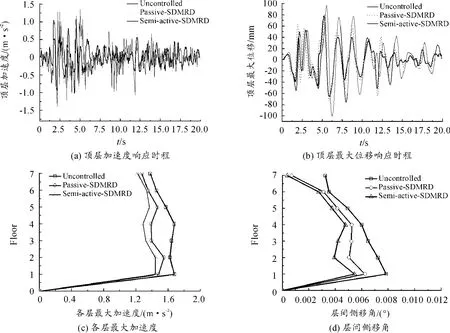
图7 设防地震(0．20g)时的地震响应

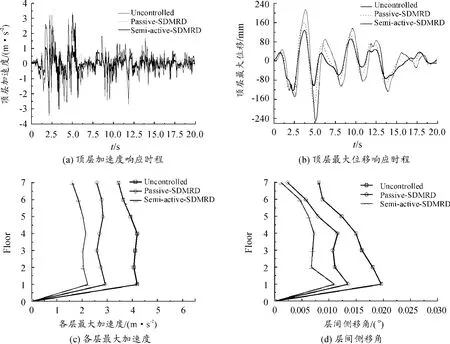
图8 罕遇地震(0．40g)时的地震响应

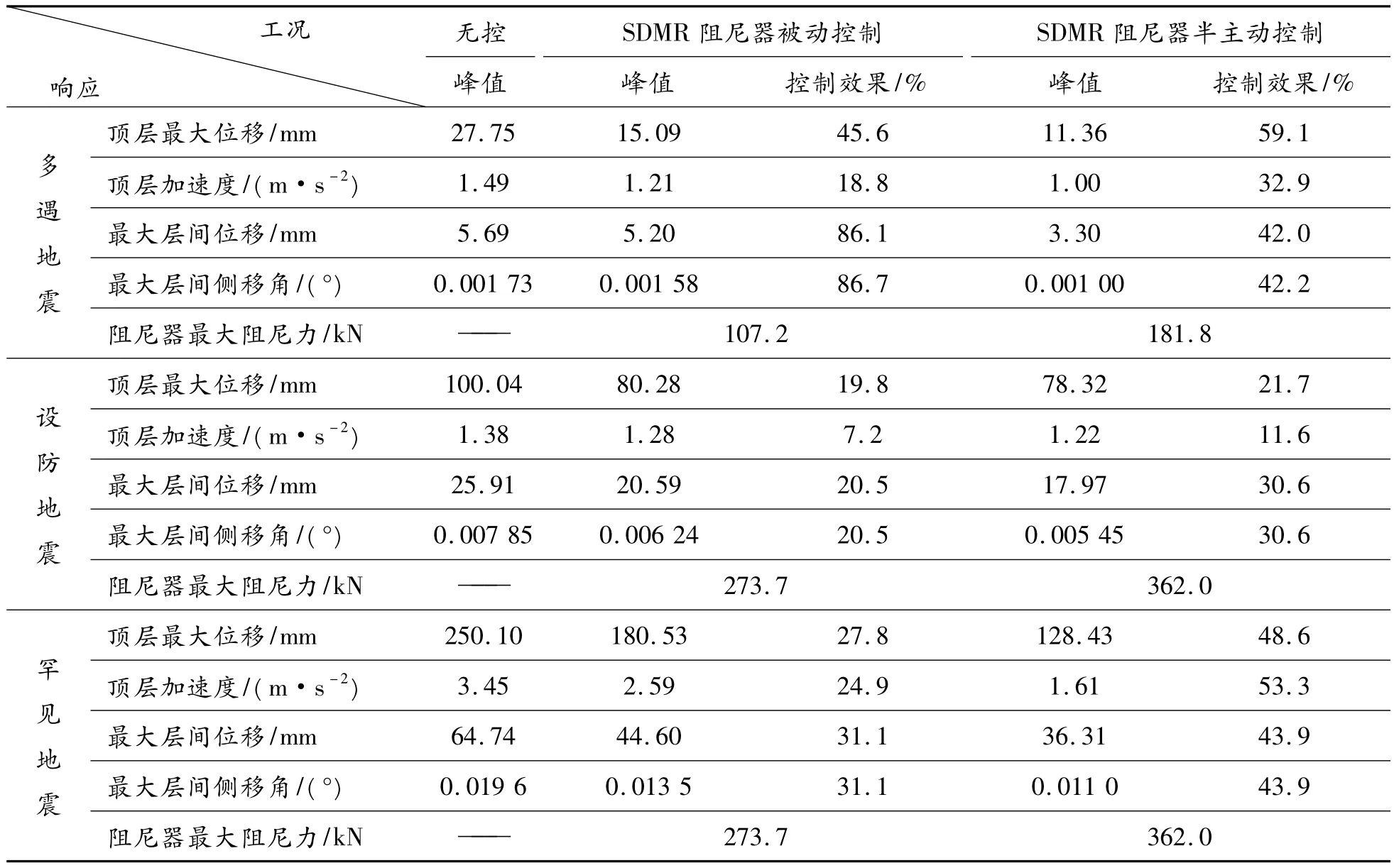
表3 多种烈度地震、不同减震措施下结构的振动响应最大值

由上述仿真结果可知:SDMR阻尼器适用于不同烈度地震下的结构振动控制。在遭遇多遇地震，结构表现为线性振动时，SDMR阻尼器工作在小行程范围内，表现为小位移、小阻尼特性，阻尼器的阻尼力可调倍数可达11.2倍，与常规设计的MR阻尼器具有相似的振动控制效果;在遭遇设防和罕遇地震，结构表现为非线性振动时，SDMR阻尼器工作在大行程范围内，表现为大位移、大阻尼特性，阻尼器的阻尼力可调倍数为0.7倍。虽然可调倍数较低，但与常规设计的MR阻尼器相比，SDMR阻尼器仍可对结构实施振动控制，这是常规阻尼器不具有的能力。此外，以上所述的这两种常规阻尼器在外部能源输入失效时将丧失半主动控制的能力，其适应性明显不如SDMR阻尼器。

5 结束语

本文基于SDMR阻尼器对建筑结构振动进行了半主动控制研究。针对某建筑结构，引入Bouc -Wen模型来反映建筑结构的非线性特征;采用基于能量的振动主动控制策略来确定结构控制力的大小;采用改进的遗传算法对SDMR阻尼器在结构中的布置位置进行了优化。在此基础上进行了基于SDMR阻尼器的结构半主动控制仿真研究。研究结果表明:SDMR阻尼器不仅对建筑结构在遭遇多遇地震(结构发生线性振动)时可实现有效控制，最大层间位移角的控制效果达42.2%;而且建筑结构在遭遇罕遇地震(结构发生非线性振动)时也可实现有效控制，最大层间位移角的控制效果达43.9%，其阻尼力和可调倍数比只对多遇地震(结构发生线性振动)的常规阻尼器具有更好的适应性，并提供足够的阻尼力储备。此外，在罕遇地震中外部电源失效的情况下，SDMR仍具有减振功能，可保证结构的安全。

［1］Ribakov Y，Agranovich G.Using a limited set of mr dampers for improving structural seismic response［J］. Structural Control and Health Monitoring，2015，22(4):615-630.

［2］徐晓龙.高层建筑结构的智能半主动振动控制研究［D］杭州:浙江大学，2006.

［3］Brando G，D’Agostino F，De M.Seismic performance of MR frames protected by viscous or hysteretic dampers［J］.Structural Design of Tall and Special Buildings，2015，24(9):653-671.

［4］Sireteanu T，Mitu A M，Giuclea M，et al.A comparative study of the dynamic behavior of Ramberg-Osgood and Bouc-Wen hysteresis models with application to seismic protection devices［J］.Engineering Structures，2014，76: 255-269.

［5］姜群，晏雨.改进的遗传算法在TSP问题中的应用［J］.重庆理工大学学报:自然科学版，2012，26 (9):96-99.

［6］于国军，杜成斌，万发学.高耗能自解耦式MR阻尼器的设计及性能试验［J］.振动、测试与诊断，2012，32 (3):426-431.

［7］Du C B，Wan F X，Yu G J.A magnetic flux leakage study of a self-decoupling magnetorheological damper［J］. Smart Materials and Structures，2015，20(6):065019.

［8］Baber T T，Wen Y K.Random vibration hysteretic，degrading systems［J］.Journal of the Engineering Mechanics Division，1981，107(6):1069-1087.

［9］Loh C H，Chung S T.A three-stage identification approach for hysteretic systems［J］.Earthquake engineering &structural dynamics，1993，22(2):129-150.

［10］周星德，杜成斌，林小国，等.非线性建筑结构振动控制研究［J］.应用力学学报，2008，25(1):38-41.

［11］Min K W，Hwang J S，Lee S H，et al.Probabilistic approach for active control based on structural energy［J］. Earthquake engineering&structural dynamics，2003，32 (15):2301-2318.

［12］田莉，陈换过，祝俊，等.基于自适应模拟退火遗传算法的传感器优化配置研究［J］.振动工程学报，2012，25(3):238-243.

［13］周莹.改进遗传算法优化无线传感器网络路由算法［J］.激光杂志，2015(1):113-116.

［14］兰胜坤.遗传算法优化BP神经网络的说话人识别系统［J］.重庆理工大学学报:自然科学版，2013(10):91 -95.

［15］张婉琳.遗传算法优化支持向量机的交通流量预测［J］.激光杂志，2014(12):116-119.

［16］吴霄，肖汝诚.基于遗传算法的大跨度混合梁斜拉桥索力优化［J］.江苏大学学报:自然科学版，2014(6): 722-726.

［17］于建平，杜纲.一类双层规划问题的遗传算法求解［J］.重庆理工大学学报:自然科学版，2014(3):93 -98.

［18］郭秀红.基于遗传算法的配送车辆路径规划［J］.四川兵工学报，2013(1):94-96.

［19］祁虔，罗婷，刘枫，等.基于遗传算法的倒立摆系统模糊九点控制器参数优化［J］.西南大学学报:自然科学版，2014(11):191-200.

［20］徐岩，郅静.基于改进自适应遗传算法的PMU优化配置［J］.电力系统保护与控制，2015(2):55-62.

(责任编辑陈 艳)

Research of Architectural Structures Semi-Active Control Based on SDMR Damper

YU Guo-jun，SUN Hu，SU Bo，CAO Li-lin
(Faculty of Civil Engineering and Mechanics，Jiangsu University，Zhenjiang 212013，China)

Semi-Active control analysis of the nonlinear vibration of architectural structures were processed based on SDMR damper.The Bouc-Wen model was used for reflecting the nonlinear characteristics of an architectural structures.The control force of the structure was determined based on the strategy of energy active vibration control.The improved genetic algorithm was used to optimize the arrangement of the position for SDMR dampers in structures.Then，the numerical simulation for the semi-active control of SDMR damper was analyzed.The simulation results show that SDMR dampers can realize the effective control to the building structure encountered often-met earthquake(structure in linear vibration)and the building structure encountered in the rarely-met earthquake(structure in non-linear vibration)，and provide sufficient reserves of damping force.

SDMR damper;semi-active control;the improved genetic algorithm;earthquake

TU591;TP315.9

A

1674-8425(2015)11-0042-09

10.3969/j.issn.1674-8425(z).2015.11.008

2015-07-11

国家自然科学基金资助项目(51508237，51408267);江苏省自然科学基金资助项目(BK20140560);江苏大学高级专业人才科研启动基金资助项目(14JDG161，14JDG162)

于国军(1981—)，男，博士，讲师，主要从事工程结构抗震、磁流变智能器件研究。

于国军，孙虎，苏波，等.基于SDMR阻尼器的建筑结构半主动控制研究［J］.重庆理工大学学报:自然科学版，2015(11):42-50.

format:YU Guo-jun，SUN Hu，SU Bo，et al.Research of Architectural Structures Semi-Active Control Based on SDMR Damper［J］.Journal of Chongqing University of Technology:Natural Science，2015(11):42-50.