商用车驾驶室悬置系统优化

谢 柯,曾发林,李建康,王在波

(江苏大学 汽车与交通工程学院，江苏 镇江 212013)



商用车驾驶室悬置系统优化

谢 柯,曾发林,李建康,王在波

(江苏大学 汽车与交通工程学院，江苏 镇江 212013)

在多体动力学软件ADAMS中建立商用车驾驶室悬置系统虚拟样机模型，选取驾驶室悬置刚度和阻尼参数以及位置参数为设计变量，以驾驶室综合加权加速度均方根值、俯仰加速度均方根值、侧倾加速度均方根值和后悬置减振器夹角为优化目标，驾驶室前后悬置动挠度为约束条件，利用软件ISIGHT搭建优化平台，采用MIGA算法对行驶平顺性进行多目标优化，得到驾驶室悬置结构参数最优解集。在此基础上，优化分析后悬置水平与垂向减振器夹角对驾驶室隔振的影响，再通过权重系数与比例系数对各优化目标进行权衡，以此提高商用车的振动舒适性。

MIGA算法；驾驶室悬置；优化匹配； 平顺性

随着目前对商用车品质的要求越来越高，商用车的平顺性问题越发受到关注。虚拟样机技术的发展对汽车性能的研究和开发起到了越来越重要的作用[1-2]。驾驶室的悬置系统是影响平顺性的重要方面，而通过对驾驶室的悬置参数优化匹配可以达到提高商用车平顺性和舒适性的目的[3-4]。

在对商用车平顺性的研究中，大多只考虑了驾驶室垂直方向的振动，对驾驶室的侧倾和俯仰振动考虑较少。本文以驾驶室综合加权加速度均方根值、俯仰加速度均方根值和侧倾加速度均方根值为优化目标，研究驾驶室垂向、俯仰和侧倾振动。ADAMS虚拟样机技术软件作为现阶段较成熟的机械系统动力学仿真软件正受到越来越多的汽车设计人员的关注。由于ADAMS提供的优化方法不能很好地进行有效概率意义的全局搜素，因此本文通过集成多学科优化软件Isight，ADAMS和Matlab，采取多岛遗传算法对驾驶室悬置系统进行多目标优化匹配，以此提高商用车舒适性，其结果具有一定的工程应用参考价值。

1 整车模型与路面的建立和验证

1.1 整车模型与路面的的建立

根据某款商用车拓扑关系及企业提供的主要参数，在ADAMS/Car中将半挂牵引车划分为驾驶室系统、动力总成、前悬架系统、后悬架系统、货箱、转向系统、制动系统和轮胎等子系统。依次对每个子系统进行建模，通过通讯器将各子系统进行装配，最后得到的半挂牵引车虚拟样机模型，如图1所示。根据《机械振动-道路路面谱测量数据报告》(GB7031—2005)[5]，推荐路面功率谱密度为

(1)

式中：n为空间频率(m-1)；n0=0.1 m-1为参考空间频率；Gd(n0)为参考空间频率n0下的路面功率谱密度，即路面不平度系数；w为频率指数，决定了路面功率谱密度的频率结构[5]。表1为A～E路面不平度系数，分级路面谱的频率指数w=2。根据表1在ADAMS中建立对应路面等级的随机路面。

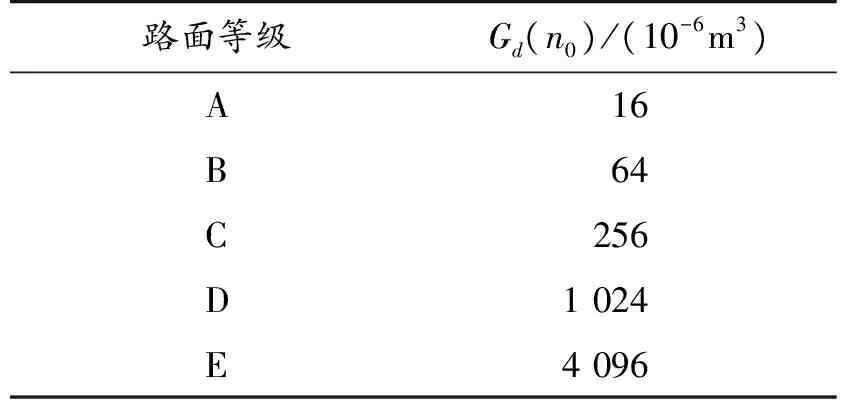
表1 道路等级和不平度系数

图1 商用车整车模型

1.2 整车模型验证

按照《汽车平顺性试验方法》(GB/T4970—2009)[6]，样车在满载情况下分别以40,50,60,70,80 km/h的车速在性能路面匀速行驶一段距离，并采集座椅椅垫上方、座椅靠背、脚背地板上的3个方向的振动，按照随机输入行驶评价指标计算得到综合加权加速度均方根值。在ADAMS/Car中，对应地采集满载整车模型在B级路面上分别在40,50,60,70,80 km/h速度下行驶的振动数据，计算得到仿真综合加权加速度均方根值。绘出试验与仿真综合总加权加速度均方根值随车速变化曲线，如图2所示。

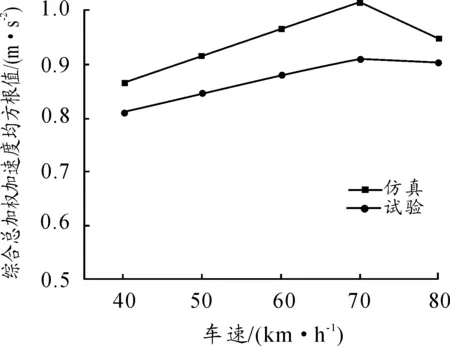
图2 商用车综合总加权加速度均方根值随车速变化曲线

由图2可见：综合加权加速度均方根值也随着车速增加而增加，仿真与试验最大误差不超过10.4%，产生误差的主要原因在于建模过程中对大部分的非线性的橡胶衬套进行了线性处理，但误差在可控范围内，可以判断模型基本正确。

2 商用车驾驶室悬置系统

2.1 商用车驾驶室悬置振动系统

考虑整车模型与优化算法耦合时优化仿真迭代时间长、效率低的特点，本文在整车模型的基础上单独调出驾驶室悬置系统模型进行优化匹配。此商用车的驾驶室采用全浮式驾驶室，在悬置4点处采集加速度信号作为激励信号。

驾驶室振动问题比较复杂，需要根据具体的研究问题简化振动系统，使之能够反映驾驶室振动特性。首先建立驾驶室悬置系统。视驾驶室主要部件为刚体。实车中存在大量的连接衬套，这些衬套都是非线性材料的橡胶衬套，在建模时需要对橡胶衬套进行线性处理[7]。建模需要考虑到衬套主要方向和转动的影响，驾驶室悬置振动系统简化成约束多刚体系统，建立的振动系统模型如图3所示。图3中：{xii(t)}i=1,2,3,4}分别为半挂牵引车驾驶室4点悬置处的激励输入；M1分别为驾驶室的质心位置；z为驾驶室的垂向位移；ψ为驾驶室俯仰角；θ为驾驶室侧倾角。

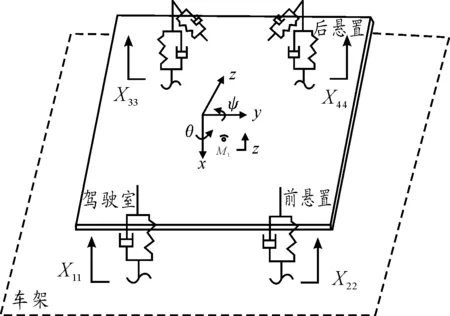
图3 驾驶室悬置振动系统模型

根据随机振动理论[8]，假设驾驶室悬置系统在4点处的激励相互独立，其相应的激励和功率谱分别为x11,x22，x33和x44,那么在仅考虑驾驶室垂直方向加速度时其输出功率谱可表示为

(2)

式中：Szz(f)为驾驶室的输入功率谱密度矩阵，且为对角矩阵，表示为

H(f)为系统的传递函数矩阵，可表示为

相应的驾驶室垂直方向的均方根值可由下式得出：

根据得到垂向振动，分析出参数对振动响应的影响，继而优化驾驶室悬置振动系统。

2.2 建立驾驶室多体动力学模型

通过驾驶室悬置振动系统的分析，需要在ADAMS中建立驾驶室的动力学模型。在ADAMS中对驾驶室悬置系统进行参数化建模，模型包括驾驶室前悬置、后悬置、座椅、驾驶员等。部件之间通过线性衬套连接。后悬置结构如图4所示，横向垂向减振器之间的夹角即为后悬置之间的夹角β。

图4 驾驶室后悬置结构

在驾驶室模型4点悬置处给出来自整车仿真的激励信号。建好的全浮式驾驶室悬置系统多刚体动力学模型，如图5所示。

3 驾驶室悬置系统多目标优化

3.1 多岛遗传算法(MIGA)

遗传算法(genetic algorithm)是一类基于生物界的适者生存的进化规律演化而来的随机化搜索方法[9-13]。选择算子、交叉算子、变异算子是遗传算法的主要3个进化算子。在遗传算法在应用过程中容易产生早熟现象，将严重地影响遗传算法的应用效果。

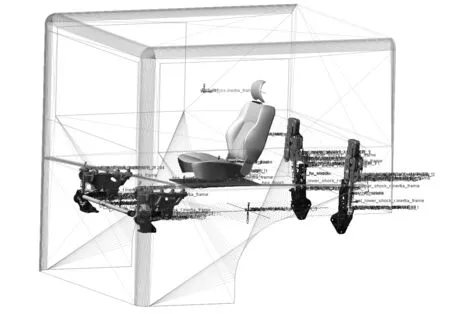
图5 驾驶室悬置系统多刚体动力学模型

本文采用岛屿模型进行子群体之间信息的伪并行算法(即多岛遗传算法)[14]。它有别于传统遗传算法，把种群分为若干个子种群，这些子种群被称为“岛屿”。在每个“岛屿”上按照传统遗传算法进行独立的选择、交叉、变异。定期在各个岛屿上随机选择一些个体“迁移”到别的“岛屿”上，通过迁移周期和迁移率这2个参数来控制整个迁移过程。通过多岛遗传算法的“岛屿”与“迁移”策略的控制，可加强全局搜索能力，避免局部最优。多岛遗传算法示意图如图6所示。

图6 多岛遗传算法示意图

3.2 多集成系统优化

本文基于Isight平台，集成软件ADAMS、Matlab及多岛遗传算法，通过优化计算在三者之间进行数据交互，得到最优解集。集成软件之间的数据流图如图7所示。

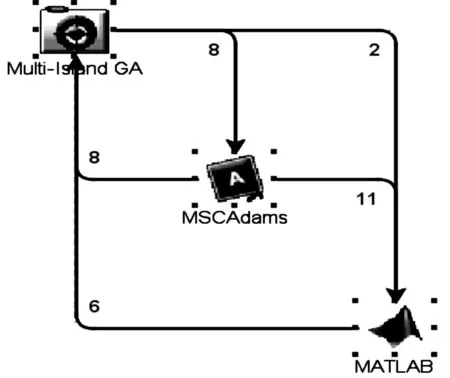
图7 软件集成数据流图

3.3 优化数学模型的建立

由于影响驾驶室隔振因素很多，本文取主要影响因子作为试验因子。在此选择驾驶室前悬置系统的刚度与阻尼、驾驶室后悬置系统的垂向横向减震器刚度与阻尼，以及横向垂向减震器上点位置坐标共8个设计变量。驾驶室悬置系统的约束条件为前后悬置的动扰度。参照企业试验车辆驾驶室悬置系统技术指标，将动挠度设为小于 50 mm 。

采用驾驶室综合加权加速度均方根值以及座椅俯仰角和座椅侧倾角的角加速度均方根值作为整车行驶平顺性优化目标，并考虑后悬置横向和垂向减振器之间夹角对驾驶室隔振的影响。其中夹角大小通过后悬置减振器的位置坐标来控制。对驾驶室悬置系统进行优化的数学模型可描述为：

式中:az为车速在70 km/h时驾驶室加权加速度加速度均方根值；θ为车速在70 km/h时座椅支撑面俯仰角加速度均方根值；ψ为车速在70 km/h时座椅支撑面侧倾角加速度均方根值；dqr,ql,dhxr,hxl为驾驶室前后悬置动挠度；kqxr,qxl,khxr,hxl为驾驶室前后悬置刚度；cqx,hx为驾驶室前后悬置阻尼；β为驾驶室后悬置夹角；Y1,Y2为驾驶室后悬置上点位置坐标。

3.3.1 模型参数设计

通过驾驶室悬置系统数学模型确定设计变量时，应根据企业生产能力、保证模型达到静平衡以及悬置设计的基本原则确定设计变量的比例范围，如表2所示。

多岛遗传算法通过控制迁移率和迁移周期两个变量保证种群的多样性，以此提高全局收敛性。迁移率是指岛上种群有多大的概率进行迁移。迁移周期是指被选中的个体需要多久将迁往到其他岛屿。迁移率和迁移周期分别设定为0.01和5。

表2 设计变量

3.3.2 目标比例因子的选取

在对驾驶室悬置系统进行多目标优化时，需要考虑目标比例因子的选取。在ISIGHT下进行多目标优化时会将所有目标取其加权和作为ISIGHT总的目标函数Objective：

Objective=Sum(WF*Xi/SF)

(3)

式中：WF为权重因子；SF为比例因子；Xi为目标值。

当多目标在不同数量级时，会导致其中某一目标起的作用很小，甚至可以忽略。要想使用ISGHT恰当地求解多目标优化问题，就必须定义合适的权重与比例因子。目标值比例因子设置如表2所示。

表2 目标值比例因子

3.3.3 后悬置减振器夹角对驾驶室隔振的优化分析

通过改变驾驶室后悬置水平和垂向减震器上点的横坐标与纵坐标的位置改变水平和垂向夹角。优化得到最优解集如图8所示。

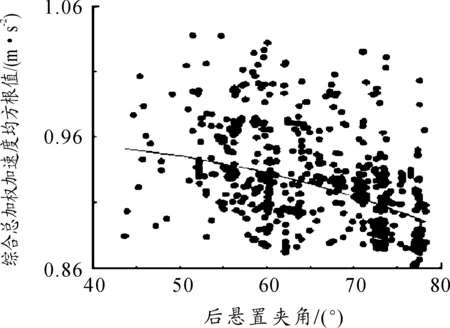
图8 后悬置减振器夹角最优解集

从图8可以明显看出：随着后悬置之间的夹角越来越大，综合总加权加速度均方根值的分布也越来越集中，并且越来越小，可近似认为后悬置水平和垂向之间的夹角和驾驶室加权加速度均方根值成反比的关系。当后悬置减振器夹角达到70°～ 80°时，综合总加权加速度基本趋于最小值，并趋于收敛。

3.3.4 分析多目标之间关系与影响

优化模型采取多目标优化，优化目标为驾驶室加权加速度均方根值、驾驶室侧倾加速度均方根值、驾驶室俯仰加速度均方根值。优化后3目标值之间的关系如图9所示。

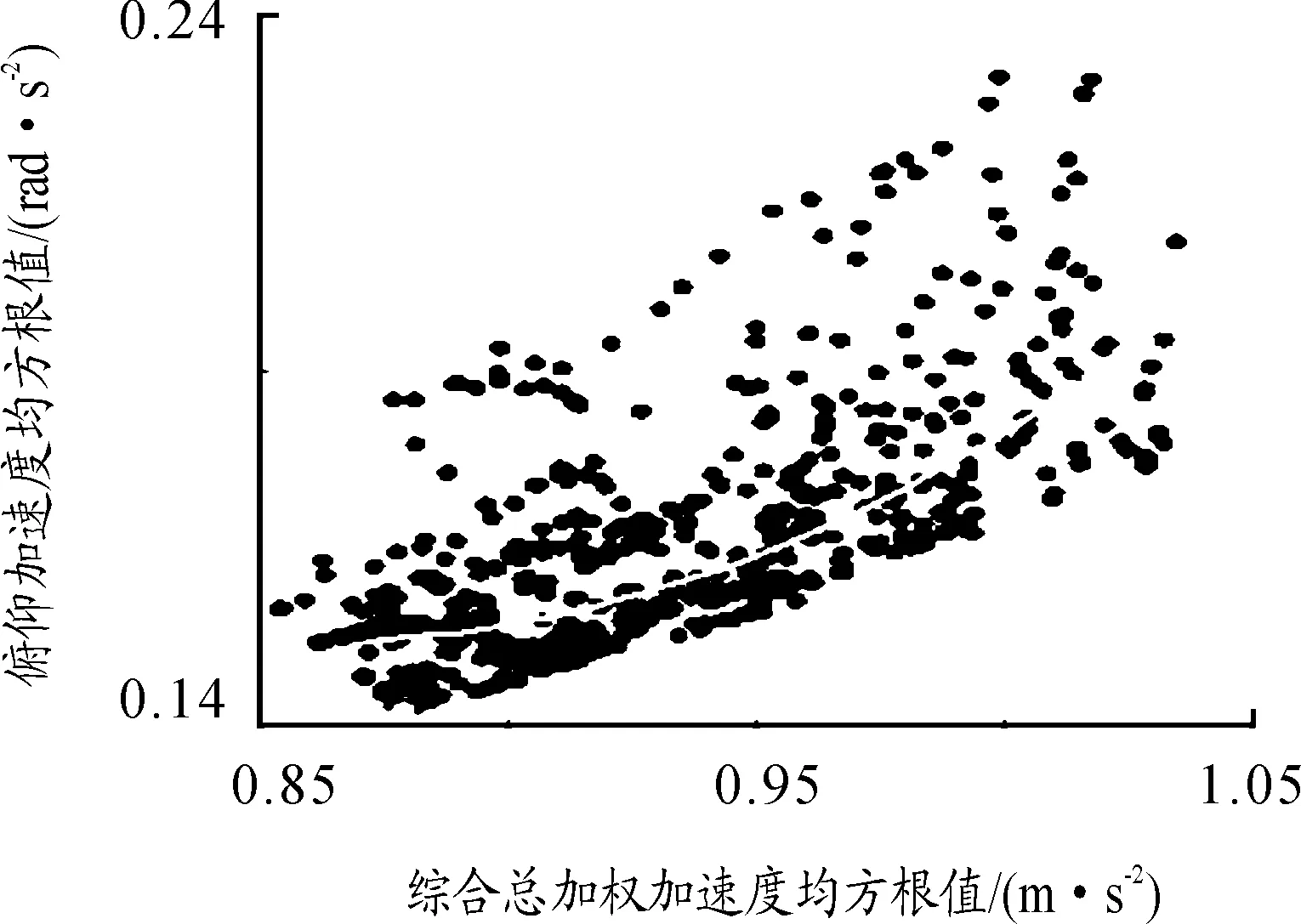
图9 多目标优化后目标值之间的关系

如图9所示，驾驶室的综合总加权均方根值和座椅处俯仰加速度均方根值分布均匀，两者基本呈正比关系。如图10所示，随着综合总加权均方根值的增加，座椅处俯仰加速度均方根值也在增加；随着侧倾加速度均方根值的不断减小，驾驶室的综合总加权均方根值大致呈现下降的趋势，可以基本认为两者成一个反比关系。由此可以得出3标值之间不能同时满足最小的可能性，即三者之间的矛盾性，继而考虑多工况下的多目标优化。

3.3.5 考虑多工况下的多目标的优化

进行多目标优化时，一个目标优化必然要以牺牲其他目标的优化作为代价，继而考虑到一些工程应用，根据实际情况，采用权重考虑优化方案。本文采取4种优化方案：第1，2组解分别倾向于优化侧倾和俯仰的振动特性；第3组解倾向于优化驾驶室的加权加速度均方根值；第4组解则是综合考虑前三者的优化。优化结果如表3所示。

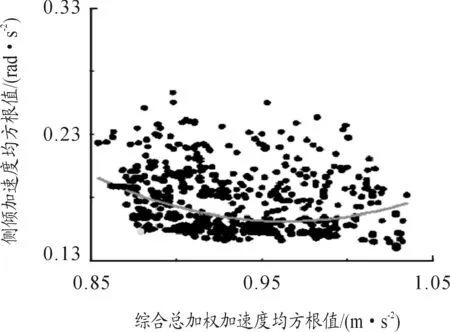
图10 综合加权加速度均方根值随驾驶室侧倾均方根值变化关系

KqxKhxcxKhxspCqxChxcxChxspβ(°)ψ/(rad·s-2)θ/(rad·s-2)αz/(rad·s-2)W1．0001．0001．0001．0001．0001．00060．000．1990．1880．998W10．9210．8070．8800．7790．6681．18571．650．1460．1520．922W20．8100．8760．8670．6780．6670．74576．130．1530．1420．879W30．8070．8071．0680．7350．6691．31077．040．1460．1470．884W40．8190．8451．0200．6750．6671．26478．450．1480．1430．878

从表3可以明显看出，各目标值都有不同程度的下降：俯仰特性幅值最大降低24.5%,平均下降22.3%；侧倾特性幅值最大降低26.6%，平均下降25.5%；综合加权加速度均方根值最大降低12.0%，平均下降10.7%；后悬置减振器之间的夹角也有不同程度的变化，最大增加30%，平均增加了26.3%。由此可见，驾驶室悬置系统性能得到了提高。

4 结论

1) 以某国产商用车为研究对象，建立了带有全浮式驾驶室的整车虚拟样机分析模型，并通过整车平顺性试验验证了模型的正确性。单独建立驾驶室悬置振动系统，根据振动系统建立驾驶室悬置多体动力学模型。

2) 在多学科优化软件平台下集成多岛遗传算法和ADAMS、Matlab软件，对商用车驾驶室悬置系统进行了多目标平顺性优化研究，同时分析了俯仰特性、侧倾特性以及综合总加权均方根值之间的矛盾性,研究了后悬置减振器之间夹角对驾驶室振动的影响。

3) 考虑到多目标之间的矛盾性，根据权重系数与比例系数对驾驶室悬置系统进行决策优化分析。结果表明：俯仰特性幅值平均下降22.3%；侧倾特性幅值平均下降25.5%；综合加权加速度均方根值平均下降10.7%。驾驶室悬置系统的性能得到了很好的提高，提高了商用车的舒适性，具有一定的工程应用参考价值。

[1] 祖旭,黄洪钟,张旭.虚拟样机技术及其发展[J].农业机械学报,2004,35(2):168-171.

[2] 杜平安,于德江,岳萍.虚拟样机技术的技术与方法体系研究[J].系统仿真学报,2008,19(15):3447-3451.

[3] 李鹏飞，马力，何天明，等.商用车驾驶室悬置隔振仿真研究[J].汽车工程，2005,27(6):740-743.

[4] 王楷焱.商用车驾驶室悬置系统动力学仿真、优化与试验研究[D].长春：吉林大学，2008.

[5] GB/T7031—2005,机械振动道路路面谱测量数据报告[S].

[6] GB /T4970—2009，汽车平顺性试验方法[S].

[7] 张志伟.商用车驾驶室悬置系统动力学仿真分析与试验研究[D].长春:吉林大学，2007.

[8] 余志生.汽车理论[M].北京:机械工业出版社，2006.

[9] 吉根林.遗传算法研究综述[J].计算机应用与软件,2004，21(2):69-73.

[10]祁虔，罗婷，刘枫，等.基于遗传算法的倒立摆系统模糊九点控制器参数优化[J].西南大学学报:自然科学版,2014(11):191-200.

[11]于建平，杜纲.一类双层规划问题的遗传算法求解[J].重庆理工大学学报:自然科学版，2014(4)：93-98.

[12]曾瑛，蒋康明，杨娇，等.基于量子遗传算法的电力通信网路由选择策略[J].太原理工大学学报,2013(4):501-505.

[13]孙颖，李秋锋， 黄丽霞，等.模拟退火遗传算法在混凝土层析成像中的应用[J].压电与声光,2013(4):487-490,495.

[14]石秀华,孟祥众,杜向党,等.基于多岛遗传算法的振动控制传感器优化配置[J].振动、测试与诊断,2008,28(1) :62-65.

(责任编辑 刘 舸)

Research for Commercial Vehicle Cab Suspension System Optimization

XIE Ke, ZENG Fa-lin, LI Jian-kang, WANG Zai-bo

(School of Automotive and Traffic Engineering, Jiangsu University, Zhenjiang 212013, China)

The virtual prototype model of commercial vehicle cab suspension system in multi-body dynamics software Adams was built, and the cab suspension stiffness and damping parameters and positional parameters were select as design variables, and the weighted RMS of acceleration and pitch acceleration root mean square value and the roll acceleration root mean square value and the angle between suspension shock absorber were built as the optimization goals, taking the cab suspension dynamic deflection as constraint conditions, and the software ISIGHT optimization platform was built, through which optimal solution set of cab suspension structure parameters was obtained. On this basis, the optimization analysis of the angel between after horizontal shock absorber and vertical shock absorber influence on vibration isolation was carried, and the optimization goal of weight coefficient and proportionality coefficient were weighted, through which to improve the ride comfort of the commercial vehicle.

MIGA; cab suspension; optimization; ride

2014-11-26 作者简介：谢柯(1990—)，男，江苏人，硕士研究生，主要从事车辆振动与噪声研究。

谢柯,曾发林,李建康,等.商用车驾驶室悬置系统优化[J].重庆理工大学学报：自然科学版，2015(3):15-20.

format：XIE Ke, ZENG Fa-lin, LI Jian-kang, et al.Research for Commercial Vehicle Cab Suspension System Optimization [J].Journal of Chongqing University of Technology:Natural Science,2015(3):15-20.

10.3969/j.issn.1674-8425(z).2015.03.004

U461.4

A

1674-8425(2015)03-0015-06