IEC 61373两个版本标准的振动试验量级对比分析
秦建忠,宋桂环,李 杰
(1.今创集团股份有限公司,常州 213011; 2.天津航天瑞莱科技有限公司上海分部,上海 201199)
IEC 61373两个版本标准的振动试验量级对比分析
秦建忠1,宋桂环2,李 杰2
(1.今创集团股份有限公司,常州 213011; 2.天津航天瑞莱科技有限公司上海分部,上海 201199)
通过对IEC 61373-1999与IEC 61373-2010铁路应用机车车辆设备冲击和振动试验试验标准的比较,主要分析了振动试验中的模拟长寿命试验的量级变化。两种版本振动试验量级变化的原因是标准中采用的S-N模型发生变化,从而导致计算加速度比的方法有所改变。
加速度比;RMS;疲劳强度曲线
概述
随着我国高速铁路网的不断完善,铁路轨道交通行业的不断发展,由于轨道运行环境的影响,车上的设备将承受振动冲击的环境。列车运行所产生的环境振动影响越来越受到业内人士的关注,为了保证设备的质量,应模拟设备使用环境条件对其进行振动冲击试验。IEC 61373是轨交行业的通用性振动冲击试验标准,标准中涵盖了模拟长寿命试验(Simulated long-life test)、冲击试验(Shock test)和功能性随机试验(Functional vibration test),其中模拟长寿命试验采用加速振动应力的方式,通过设备每个轴向5小时的振动试验来等效25年正常运行的振动疲劳损伤。随着对铁路机车车辆设备的试验考核要求越来越高和对产品结构疲劳损伤模型认识的不断提高,IEC 61373也在作相应的修正。
目前,国内所使用的试验标准处于IEC 61373-1999[1]和IEC 61373-2010[2]共用的情况。相应的国内现行的标准TB/T 3058-2002[3],GB/T 21563-2008[4]沿用了IEC 61373-1999。为了使试验人员对两个版本的试验标准有较为清晰的认识,本文从原理入手,解释了试验标准的区别。
1 IEC 61373-2010与IEC 61373-1999的区别
根据两个版本标准的对比,功能性随机振动试验与冲击试验的试验量级保持不变,而模拟长寿命试验的振动量级发生了较大的变化,变化情况见表1。由表1中可以看到,两个版本的标准中,当试验件属于1类或2类安装的产品时,模拟长寿命试验的振动均方根值下降幅度为27%~29%,而试验件属于3类-车轴安装的产品时,振动均方根值的下降幅度为52%~53%。究其原因,模拟长寿命试验的振动量级是通过功能性随机振动试验的量级按一定比例(即加速度比)放大,从而缩短试验时间。量级变化,主要是由于加速度比发生了变化。
2 两种版本标准中加速度比的计算方法
2.1 IEC 61373-1999
为缩短试验时间,该标准选择增加振幅的方法,为进行模拟长寿命随机振动试验。假定试验件的疲劳损伤D与应力的指数及循环次数成正比见式(1)。

式中:
Nf—循环次数 ;
Σ— 应力水平;
m— 指数/加速因子(典型值为3-9);
α—常数。
由于随机振动的均方根值可正比于应力水平,试验时间可正比于循环次数,因此

式中:
Ts—实际服役时间(寿命);
Tt—试验时间;
As—实际运行加速度均方根值;At—试验加速度均方根值。
可根据式(2),定义加速度比r为

当产品的实际考核寿命按照25年计时,实际服役时间Ts=25%正常寿命=25年寿命×300天/年×10h/天×25%=18750h,试验时间Tt定为5h,加速因子m按照典型金属取为4,则此时加速比r为
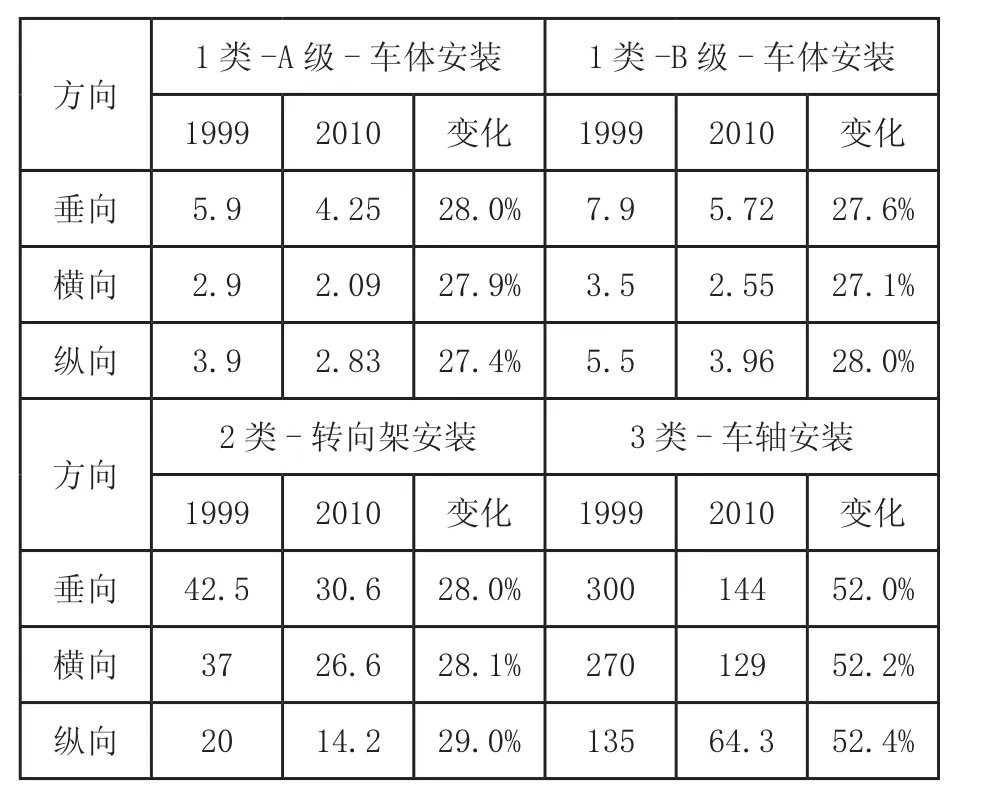
表1 标准中模拟长寿命试验条件对比

该版本与1999版所采用的模拟长寿命试验量级计算思路是相同的,都是通过增加振幅来缩短试验时间。同时,对于产品疲劳损伤D的定义也基本相同,见式(5)。

式中:
Nf— 循环次数;
Δσ— 应力范围(或者说交变应力幅值);
m— 指数(典型值为3~9);
α— 常数。
然而相对于1999版中简单的反幂律S-N模型,2010版中引入了恒幅疲劳极限(Constant amplitude fatigue limit)和截止极限(Cut-off limit),按照循环次数的范围分为3段,详见图1。当Δσ大于恒幅疲劳极限时(N<5×106),S-N曲线与1999版本相同,可定义在常数α1下,满足

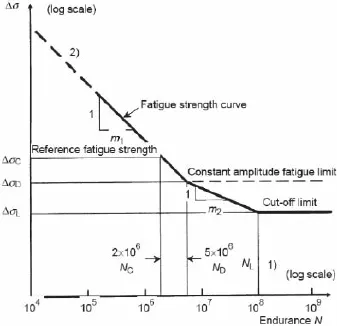
图1 典型S-N曲线
式中:m1为1999版本中的m相对应,典型取值为3~9,对于典型金属,取值为4。
当Δ σ小于恒幅疲劳极限且大于截止极限时(5×106<N<1×108),S-N曲线可定义在常数α2下,满足

式中:m2=m1+2。
当Δσ小于截止极限时,S-N模型认为产品在疲劳载荷下不会有损伤,N为无穷大。
为了保证车辆设备的实际运行寿命和5个小时的试验时间内所造成的疲劳损伤程度相同,根据ASD曲线的最小频率来确定循环次数,见表2。
从表2中可以看到,试验循环数处于S-N曲线的第1段,而服役循环数处于S-N曲线的第2段。此时,交变应力幅值Δσ还是对应于加速度均方根值,则加速度比r可表示为
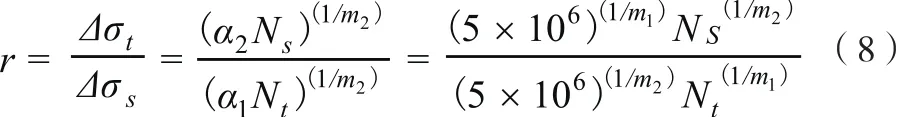
对于1、2类,Nt=0.036×106,通过式(8)计算得出,加速度比r为5.66。同理,可算出3类的加速度比r为3.78。
3 结束语
由于标准中选用的疲劳模型不同及对循环次数的定义发生变化,导致计算加速振动量级时的加速度比从原来1999版的7.83下降为2010版的5.66(1类、2类)和3.78(3类),从而使模拟长寿命试验的均方根值减小了27%~29%(1类、2类)和52%~53%(3类)。
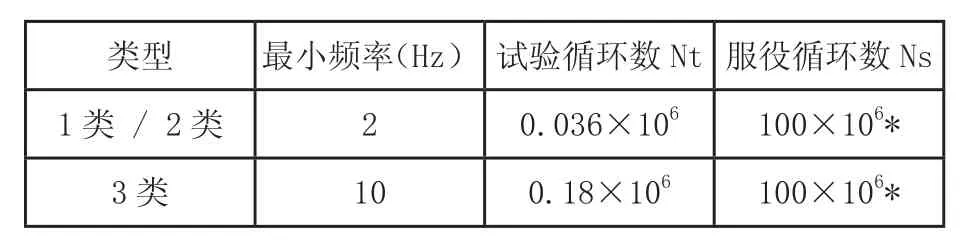
表2 试验循环次数及服役循环次数
由于标准中试验量级的降低,按照相同的反幂律计算方式,从试验时间的角度考虑,对于1类和2类车辆设备,2010版的5h只相当于1999版中的26%左右,而对于3类车辆设备,2010版的5h只相当于1999版中的5%左右。一般地,对于相对成熟的车辆设备来说,采用IEC 61 373-2010进行型式试验,可以适当地弱化对产品结构强度的要求,降低制造成本;而对于技术、工艺等都不成熟的车辆设备,考虑到国内实际列车运行环境与国际标准的差异,可以仍然沿用IEC 61373-1999(或TB/T 3058-2002,GB/T 21563-2008),以防止试验时的欠考核。
另外,由于IEC 61373-2010的S-N曲线中,Δσ主要为对称循环(R= -1)中的应力幅值,可以直接对应到产品所受到的加速度均方根值。而对于像列车行李架,污水箱等列车部件,在模拟长寿命试验中的应力值并非是对称循环的,必须考虑平均应力的影响。平均应力会使得疲劳寿命下降[5],因此在更细致地考虑类似产品的疲劳寿命及加速振动试验时是比较重要的。
[1] IEC 61373-1999, Railway applications - Rolling stock equipment -shock and vibration tests [S].
[2] IEC 61373-2010, Railway applications - Rolling stock equipment -shock and vibration tests [S].
[3] TB/T 3058-2002,铁路应用 机车车辆设备冲击和振动试验 [S].
[4] GB/T 21563-2008,铁路应用 机车车辆设备冲击和振动试验 [S].
[5] 陈传尧. 疲劳与断裂 [M]. 武汉:华中科技大学出版社, 2005.
秦建忠 ( 1966年7月- ),本科,工程师,主要研究方向:轨道交通产品可靠性。
Comparison of Vibration Level Between Two Versions of IEC 61373
QIN Jian-zhong1, SONG Gui-huan2, LI Jie2
(1.KTK GROUP Co., Ltd., Changzhou 213011; 2.Shanghai Branch of Tianjin Aerospace Ruilai Technology Co.,Ltd., Shanghai 201199)
Through comparison of IEC 61373-1999 and IEC 61373-2010, Railway applications - Rolling stock equipment - Shock and vibration tests, the change of vibration level of simulated long-life test is mainly analyzed. The reason of difference is explained in according to the calculation of the acceleration ratio, which is caused by change of S-N modal used in the standard.
acceleration ratio; RMS; fatigue strength curve
O324
A
1004-7204(2015)03-0054-03

