浅谈高中数学教学中学生思维的培养

（甘肃省兰州新区永登五中730311）

浅谈高中数学教学中学生思维的培养

薛东梅

（甘肃省兰州新区永登五中730311）

我们知道，高中数学学科知识的系统性、推理的严密性对培养学生的逻辑思维能力很有好处。同时，如果我们在教学中努力践行一题多解或是一题多变的教学方法，对培养学生的发散思维也不无益处。前不久，笔者有幸参加了我县高中数学优质课教学观摩活动，聆听了十几位优秀教师的观摩课，对他们在课堂上引导学生从不同的角度去求解，或是将一道题目变化出多种形式供学生思考，积极培养学生思维的教学方法留下了深刻印象。现将此次观摩活动中一些精彩之处实录如下，以飨读者。

一、一题多解训练学生数学思维

在第一堂观摩课上，教师板书了例题：

例：已知x、y≥0且x+y=1，求x2+y2的取值范围。

先让学生通过小组合作解答。很快，一学生上台写出了如下的解答方案：

解：由x+y=1得y=1-x，则

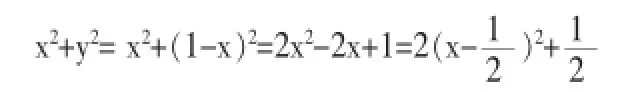
由于x∈[0，1]，根据二次函数的图象与性质知

（笔者注：在这个解题过程中，该生通过变量替换的方法，将二元函数的最值问题，转化成一元函数来解决，使解题变得简单了，这也是我们经常倡导使用的一种数学思想方法。）

当学生以为此题已经解决，期待教师讲解新的内容时，教师却“卖关子”说此题还有更容易的解答方法。“一石激起千层浪”，学生又进入了热烈的思考、讨论、解答中。不一会，有几个学生果然运用对称换元方法，更容易地求出了最值：

解：由于x+y=1，x、y≥0，则可设

所以，当t2=0时，x2+y2取最小值；当时，x2+y2取最大值1。

如此一来，学生对该题的解答就有了两种方法，而且，这不单单是两种方法，更是两种思路。教师为了进一步拓展学生的思维，还可以将此题通过三角换元方法，转化成三角恒等式变形后来解决：

解：由于x+y=1，x、y≥0，则可设

x=cos2θ，y=sin2θ其中θ∈[0，

则x2+y2=cos4θ+sin4θ=（cos2θ+sin2θ）2－2 cos2θsin2θ cos4θ

当cos4θ=1时，x2+y2取最小值1。

这三种方法，都是通过函数观点来求最值，在解题的本质上都是一样的，只是采用了不同的换元方式而已，但一转换，就导致了化简、运算量大小不同。这种引导学生从不同的角度去求解，对一道题目从不同角度去解答，寻求多种解法，在潜移默化中有助于培养学生的数学思维和解题思路，在无形之中发展了学生的数学思维，对提高学生分析问题、解决问题的能力很有益处。此外，若是课堂上还有多余的时间，教师还可以运用基本不等式和数形结合的思想来解答此题，那样对培养学生数学思维能力更会产生积极的作用。

二、一题多变训练学生数学思维

在高中数学教学中，我们除了可以通过一题多解的方法训练学生的思维外，还可以通过将一道题目加以变化的方法，通过联想、类比、延伸，将一道题变化出许多新的题目，来训练学生的数学思维。恰好在第二堂观摩课上，授课老师就借助第一堂中的那道例题，采用一题多变的方法来训练学生的数学思维，实录如下：

例：已知x、y≥0且x+y=1，求x2+y2的取值范围。

针对上述例题，这位教师没有给学生太多的思考时间，运用前面谈到的对称换元方法求出了最值后，PPT显示了以下三个变式题，供学生思考、讨论、解答。

1：已知x、y≥0且x+y=1，能求x8+y8的取值范围吗？x8+y6呢？x7+y7的范围能求吗？

2：已知a、b为非负数，M=a4+b4，a+b=1，求M的最值。

之后，教师让学生展开讨论，利用前面例题的特殊性，逐步将学生的思维引向一般化，从而得出了一般性的结论。这种将典型例题进行充分挖掘，借助例题进行变式教学的方式，既可以很好地巩固基础知识，又可以有效地训练学生的思维能力，还可以使学生养成举一反三、触类旁通的习惯。对学生数学思维能力的提高，增强对数学学习的兴趣都是大有裨益的。

因此，在平时的高中数学课堂教学中，我们不一定非要通过题海战术来夯实学生的基础，提高学生的成绩，因为数学题是做不完的。只有采取上述的一题多解或是一题多变的方法，重在培养学生的数学思维的广度、深度，从根本上解决问题，才能事半功倍地提高数学课的教育教学质量。

如在课后给学生布置作业时，我们能否不再给学生布置大量的习题，让学生负担很重，忙于应付。我们教师完全可以将书上的一些习题进行有目的的演变，逐渐加深，让学生通过前后有联系的题目的解题，掌握一些规律。完全可以把变式题布置给学生，让学生运用一题多解，一题多变的方式来掌握一些数学知识及解题规律。

例如，在学习了抛物线后，在习题中出现了以下一题：

过抛物线y2=2px焦点的一条直线和这条抛物线相交，设两个交点纵坐标为y1，y2，求证：y1y2=-p2。（设线段AB为过抛物线焦点的弦）

此题证明并不难，但其结论却很有用，关键是运用其结论。在布置此题给学生时我们便可以有针对性地演变。如变成：

1.证明：过抛物线焦点弦两端点的切线与抛物线的准线，三点共线。

2.证明：抛物线焦点弦中点与其端点切线的交点连结线段，等于焦点弦长的一半，并且被这条抛物线平分。

3.证明：抛物线焦点弦中点与其端点切线的交点的连线，平行于抛物线的对称轴。

另外，我们还可以让学生自己变式，便还可能出现如下变式：

1.证明：抛物线的准线是其焦点弦两端点的切线的交点的轨迹。

2.证明：过抛物线焦点一端，作准线的垂线，那么垂足、原点以及弦的另一端点，三点共线。

3.证明：抛物线焦点弦两端点的切线互相垂直。

我坚信，只要我们循序渐进，逐步训练，学生的思维能力就会逐步提高，解答问题的能力自然也会得到训练，教学效果更会好一些。总之，只要我们在平时的数学课堂教学中，力求从培养学生的数学思维的角度出发，想方设法地设计教学内容，精选例题，一题多变，一题多解，相信学生的数学思维一定会得到提高的。

（责编 金东）