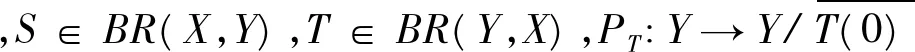多值线性算子的正则Fredholm对的分类

范亚静，蹇人宜

(1.北方民族大学 数学与信息科学学院,宁夏 银川 750021;2.陕西师范大学 数学与信息科学学院,陕西 西安 710062)



·数理科学·

多值线性算子的正则Fredholm对的分类

范亚静1,2，蹇人宜1

(1.北方民族大学 数学与信息科学学院,宁夏 银川 750021;2.陕西师范大学 数学与信息科学学院,陕西 西安 710062)

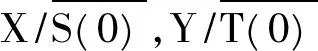
分类;正则Fredholm对;多值线性算子

多值线性算子(又称线性关系)的概念是线性算子概念的自然推广。多值线性算子的概念在20世纪50年代von Neumann当考虑非稠定线性微分算子的共轭[1]时就引入到算子理论中了。此后,在最优化与控制的问题[2-3]中也导致了对多值线性算子的研究。多值线性算子的理论和方法也用来处理偏微分方程[4]和常微分方程[5]的某些问题。多值线性算子具有很多和线性算子平行的性质,然而,由于多值性所导致的复杂性,不是线性算子的所有性质都能平移到线性关系中来,因而线性关系有很多特殊的性质,并且在研究方法上,也与线性算子不尽相同。R. Cross 的专著[6]是线性关系研究领域的一个工具包。Fredholm 算子理论在应用数学中是一个十分有用的工具,R. Cross等人将经典的 Fredholm 理论移植到线性关系中,获得了一系列十分有价值的结果[7-10]。T. Alvarez 还考虑了赋范空间中的几乎半-Fredholm 线性关系[11]。近年来,E. Boasso 讨论了正则的 Fredholm 对及其分类[12]。

本文主要讨论正则 Fredholm 关系对(S,T)在每一类中X和Y的分解式及S,T的各自表达式。 由于多值性导致的复杂性,我们不可能沿用文献 [12] 的方法。我们的目的是讨论(S,T)的正则性和分类性使它们相应的选择构成的算子对(PSS,PTT)也具有同样的性质,再利用二者之间的转化关系式,将(PSS,PTT)的相应结论转化为(S,T)的,并最终完全地获得了正则Fredholm关系对的分类。

1 预备知识

定义1[6]设U,V是任意非空集合,关系T是从U到V的映射,其定义域是U的子集D(T),且取值于2V∅。从U到V的全体关系记为R(U,V)。

定义2[6]设X,Y是数域K=R或C上的向量空间,关系T∈R(X,Y)称为线性关系(或多值线性算子)是指对于所有的x,z∈D(T)以及非零系数α∈K,有

1)T(x)+T(z)=T(x+z);

2)αT(x)=T(αx)。

定义3[6]记LR(X,Y)为从线性空间X到线性空间Y的所有线性关系构成的集合。

R(T):=T(D(T))=∪{T(x):x∈D(T)}称为T的值域;

N(T):=T-1(0)={x∈D(T):0∈Tx}称为T的核。

定义4[6]设X,Y是数域K=R或C上的向量空间,T:X→Y是线性关系,则T称为有界的是指对每个Y内0的邻域V,X的有界子集B,都存在r>0,使得

T(B)⊂T(0)+sV,∀s≥r。

记BR(X,Y)为X到Y的有界线性关系构成的集合。

定义5[13]设S∈BR(X,Y),以及T∈BR(Y,X),且S,T是闭的,并使得

a:=dimN(S)/(N(S)∩R(T)),

b:=dimR(T)/(N(S)∩R(T)),

c:=dimN(T)/(N(T)∩R(S)),

d:=dimR(S)/(N(T)∩R(S))

是有限的,则(S,T)称为多值线性算子的Fredholm对,记为(S,T)∈PR(X,Y)。

T∈L(X,Y)称为正则的,是指T是闭的,且存在闭的T′∈LR(Y,X),使得T=TT′T；又若(S,T)∈PR(X,Y)且S,T均是正则的,则称(S,T)是正则Fredholm,记为(S,T)∈RPR(X,Y)。

命题 1 如果(S,T)∈RPR(X,Y),那么下述论断等价:

(i)R(T)是X的可补子空间;

(ii)N(S)是X的可补子空间;

(iii)N(S)+R(T)是X的可补子空间;

(iv)N(S)∩R(T)是X的可补子空间;

(v)R(T)是Y的可补子空间;

(vi)N(T)是Y的可补子空间;

(vii)N(T)+R(S)是Y的可补子空间;

(viii)N(T)∩R(S)是Y的可补子空间。

定义6[6]若

T=A+T-T,D(A)=D(T),

则线性算子A称为线性关系T的选择(单值部分)。

若A是T的选择,则有

T(x)=A(x)+T(0),∀x∈D(T),

因此有R(T)=R(A)+T(0)。

由选择的定义,可以看出,R(PTT)=R(T)-T(0),若T是闭的,则T(0)是闭的,因而ker(PT)=T(0)。

2 多值线性算子的正则Fredholm对分类

以下用X,Y表示两个Banach空间。在文献 [12] 中,E. Boasso考虑了单值线性算子的正则Fredholm对的分类问题,对于多值线性算子的正则Fredholm对是否也可以考虑相应的分类呢?

定义7 设(S,T)∈RPR(X,Y),子空间序列(RS,n)n∈N和(RT,n)n∈N分别递归地定义为

RS,0=Y,RT,0=X,

若RS,n,RT,n已经定义好,则定义

RS,n+1:=S(RT,n),RT,n+1:=T(RS,n)。

这里,N是包括0的自然数。

下面给出多值线性算子的正则Fredholm对分类的一个核心概念。

定义9 设(S,T)∈RPR(X,Y),若p,q是第一个使得∀k≥0,RS,p=RS,p+k,RT,p=RT,p+k,则称n=min{p,q}为关系对(S,T)的编号。

(i)若p=q,则称关系对(S,T)是I-n型;

(ii)若p

(iii) 若p>q,则称关系对(S,T)是III-n型。这里p,q∈N,有下面3种可能情况:

(i)p=q;

(ii) 当p

(iii) 当p>q时,p=q+1。

本文观察所考虑的问题中X和Y,S与T的构造都是对称的,所以在研究多值线性算子的正则Fredholm对时,如果有必要可能会交换X和Y,S和T。那么只需考虑I-n型和II-n型的情况。

以下记P(X,Y)为Fredholm算子对构成的集合,RP(X,Y)为正则Fredholm算子对构成的集合。

(i) 若 (S,T)∈PR(X,Y),则(PSS,PTT)∈P(X,Y)。

(ii) 若 (S,T)∈RPR(X,Y),则(PSS,PTT)∈RP(X,Y)。

证 明 (i)

若 (S,T)∈PR(X,Y),则由多值线性算子Fredholm对的定义知,

a=dimN(S)/(N(S)∩R(T))<∞,

b=dimR(T)/(N(S)∩R(T))<∞,

c=dimN(T)/(N(T)∩R(S))<∞,

通过对比数据发现，使用辅助装置后测得的数据均高于开放检测的数据，由此说明使用辅助装置后测出的硫化氢含量是真实、有效的，硫化氢检测辅助可以作为生产现场硫化氢检测的重要工具。

d=dimR(S)/(N(T)∩R(S))<∞。

而我们知道

N(S)=N(PSS),

R(PSS)=R(S)-S(0),

N(T)=N(PTT),

R(PTT)=R(T)-T(0),

N(PSS)/(N(PSS)∩R(PTT))=

N(S)/(N(S)∩(R(T)-T(0)))≅

N(S)-[N(S)∩(R(T)-T(0))]=

N(S)-[(N(S)∩R(T))-

(N(S)∩T(0))]

又因为a<∞,dimT(0)<∞,所以

a0:=dimN(PSS)/(N(PSS)∩R(PTT))<∞。

由于

R(PTT)/(N(PSS)∩R(PTT))=

(R(T)-T(0))/(N(S)∩(R(T)-

T(0)))≅

R(T)-T(0)-

[N(S)∩(R(T)-T(0))]=

R(T)-T(0)-[(N(S)∩R(T))-

(N(S)∩T(0))]

以及b<∞,dimT(0)<∞,所以b0:=dimR(PTT)/(N(PSS)∩R(PTT))<∞。同理,c0:=dimN(PTT)/(R(PSS)∩N(PTT))<∞,d0:=dimR(PSS)/(R(PSS)∩N(PTT))<∞。这就说明了(PSS,PTT)∈P(X,Y)。

(ii) 因为(S,T)∈RPR(X,Y),所以(S,T)∈PR(X,Y)且S,T均是正则的线性关系。由(i)知,(PSS,PTT)∈P(X,Y),且由正则关系的定义知,存在闭的S′∈BR(Y,X),T′∈BR(X,Y)使得:

S=SS′S,T=TT′T,

故PSS=PSSS′S。简记PS=P,PS′=P0,则PS=PSS′S。因为∀x∈X,

PSP0S′PSx=

PSP0S′(S(x)-S(0))=

PSP0S′S(x)-PSP0S′S(0)=

PS(S′S(x)-S′(0))-

[PS(S′S(0)-S′(0))]=

PS(S′S(x)-S′(0))-

PS(S′S(0)⨁S′(0))=

PSS′S(x)-PSS′S(0)=

PS(x)-PS(0)=PS(x),

所以PSP0S′PS=PS,即PS是正则算子。

同理,PTT是正则算子。于是

(PSS,PTT)∈RP(X,Y)。

证毕。

以下文章中出现的PT,PS均指定理1中出现的商映射。

定理2 若(S,T)是I-n型的,则(PSS,PTT)也是I-n型的。

证 明 因为(S,T)是I-n型的,所以p=q=n,故有

RS,n=RS,n+k,RT,n=RT,n+k,∀k≥0。

第1步：先证明当n=k=1,结论成立。即当RS,1=RS,2,RT,1=RT,2时,能诱导出

RPSS,1=RPSS,2,RPTT,1=RPTT,2。

因为R(S)=RS,2=SR(T)=S(RT,2)=STRS,1=R(STS),以及

RPSS,2=PSSRPTT,1=

S(RPTT,1)-S(0)=

S(R(T)-T(0))-S(0)=

R(ST)-ST(0)-S(0)=R(ST)-ST(0),

RPSS,1=R(PSS)=

R(S)-S(0)=R(STS)-S(0),

显然S(0)⊂ST(0),所以

R(ST)-ST(0)⊂R(S)-S(0),

即RPSS,2⊂RPSS,1。又因为

R(STS)⊂R(ST),

(R(STS)-S(0))+ST(0)=R(STS),

S(0)⊂ST(0),ST(0)⊂R(STS)),

所以

(R(STS)-S(0))+ST(0)⊂(R(ST)-ST(0))+ST(0)

特别地,

R(STS)-S(0)⊂R(ST)-ST(0)。

这样RPSS,1⊂RPSS,2,故RPSS,1=RPSS,2。

同理可证RPTT,1=RPTT,2。

第2步：RS,1=RS,k+1和RT,1=RT,k+1(∀k≥0),能分别诱导

∀k≥0,RPSS,1=RPSS,k+1,RPTT,1=RPTT,k+1。

事实上,因为对于所有的k≥0,都有

RS,1=RS,2=…=RS,k+1=…。

假设当k≥1时,结论成立。那么当

RS,1=RS,k+1=RS,k+1+1,

RT,1=RT,k+1=RT,k+1+1

时,有

RPSS,k+1+1=PSS(RPTT,k+1)=

PSS(RPTT,1)=

RPSS,2=RPSS,1,

RPTT,k+1+1=PTT(RPSS,k+1)=

PTT(RPSS,1)=RPTT,2=RPTT,1,

故对于一切k≥0结论成立。

第3步:对于任意的n>1,要证在RS,n=RS,n+k,RT,n=RT,n+k之假定下,必有

RPSS,n=RPSS,n+k,RPTT,n=RPTT,n+k,∀k≥0。

假设当k=1时,即当RS,n=RS,n+1,RT,n=RT,n+1时,类似于第一段的证明可得RPSS,n=RPSS,n+1,RPTT,n=RPTT,n+1。

以此递推下去知,当

RS,n=RS,n+1=…=RS,n+k=RS,n+k+1=…,

RT,n=RT,n+1=…=RT,n+k=RT,n+k+1=…

时,有

RPSS,n=RPSS,n+1=…=RPSS,n+k=RPSS,n+k+1=…,

RPTT,n=RPTT,n+1=…=RPTT,n+k=RPTT,n+k+1=…。

证毕。

定理3 若(S,T)是II-n型的,则(PSS,PTT)也是II-n型的。

证 明 若(S,T)是II-n型的,则p=n,q=n+1,以及RS,n=RS,n+k,RT,n+1=RT,n+1+k,∀k≥0。要证∀k≥0,

RPSS,n=RPSS,n+k,RPTT,n+1=RPTT,n+1+k。

显然当k=0时，结论成立。

第1步:当n=1时,由RS,1=RS,2=RS,3=…=RS,k=RS,k+1=…,RT,2=RT,3=RT,4=…=RT,k=RT,k+1=…,以及定理2的证明过程中的第3段可得:

RPSS,2=RPSS,3=…=RPSS,k=RPSS,k+1=…,

RPTT,2=RPTT,3=…=RPTT,k=RPTT,k+1=…,

以及

RPSS,1=R(S)-S(0)=RS,1-S(0),

RPSS,2=PSS(R(T)-T(0)) =

R(ST)-ST(0)=RS,2-ST(0),

又由RS,2⊂RS,1,S(0)⊂ST(0),故RPSS,2⊂RPSS,1。又因为RS,3⊂RS,2,RS,3=(RS,3-S(0))+ST(0),以及RS,2=(RS,2-S(0))+ST(0),所以(RS,3-S(0))+ST(0)⊂(RS,2-S(0))+ST(0),因而RS,3-S(0)⊂RS,2-S(0),于是RPSS,1⊂RPSS,2。故RPSS,1=RPSS,2。从而RPSS,1=RPSS,k,RPTT,2=RPTT,2+k,∀k≥0。

第2步:∀n>1,若RS,n=RS,n+k,RT,n+1=RT,n+1+k,∀k≥0,即

RS,n=RS,n+1=…=RS,n+k=RS,n+k+1=…,

RT,n+1=RT,n+2=…=RT,n+k=RT,n+k+1=…,

则由定理2第3段证明过程知

RPSS,n+1=RPSS,n+k+1,RPTT,n+1=RPTT,n+k+1。

类似于第1段的证明有RPSS,n=RPSS,n+1,故∀k≥0,RPSS,n=RPSS,n+k,RPTT,n+1=RPTT,n+k+1,即(PSS,PTT)也是II-n型的。证毕。

定理4 若 (S,T)是III-n型的,则(PSS,PTT)也是III-n型的。

证 明 由于X与Y,S与T地位是对称的,故当交换X与Y,S与T时,由定理3便得结论成立。

(ii)Mn,S=RPSS,n∩N(T),Nn,T=RPTT,n∩N(S);

(iii)Y2n,S=RPSS,n∩Y2k,S,X2n,T=RPTT,n∩X2k,T,k=1,2,…,n-1;

(iv)(Mn,S)n∈N+,(Nn,T)n∈N分别是N(T),N(S)的下降序列,且当n≥2时是有限维的;

当n=1时,

定理5 设(S,T)∈RPR(X,Y)的编号是1。

(ii) 若(S,T)是III-1型的,则空间X,Y允许有分解:

∀x∈X1,S(x)=S(0),

由于篇幅的原因,我们省略证明。类似地,我们还可以得到(S,T)的编号为n时,空间X,Y的分解式及算子S,T的表达式。在此就不作详细叙述了。

[1]VONNEUMANNJ.FunctionalOperators[M].Princeton:PrincetonUniversityPress，1950.

[2]AUBINJPCELLINAA.DifferentialInclusions[M].Wiss:Springer-Verlag，1984.

[3]ClARKEFH.OptimizationandNonsmoothAnalysis[M].Philadelphia:SocietyforIndustrialandAppliedMathematics，1983.

[4]GROMOVM.PartialDifferentialRelations[M].NewYork:Springer-Verlag，1986.

[5]FAVINIA,YAGIA.Multivaluedlinearoperatorsanddegenerateevolutionequations[J].AnnalidiMatematicaPuraedApplicata, 1993,163(4): 353-384.

[6]CROSSRW.MultivaluedLinearOperators[M].NewYork:MarcelDebberInc，1998.

[7]CROSSRW.Anindextheoremfortheproductoflinearrelations[J].LinearAlgebraanditsApplications, 1998, 277(1): 127-134.

[8]CROSSRW.Noteonthecanonicalfactorizationofamulti-valuedlinearoperator[J].CommunicationsinAppliedAnalysis, 1999, 3(4): 461-469.

[9]CROSSRW,LABUSCHAGNELE.Characterizationsofoperatorsoflowersemi-FredholmtypeinnormedLinearspaces[J].QuaestionesMathematicae, 1992, 15: 151-173.

[10]CROSSRW,PILLAYPUbiquitouspropertiesofcertainoperationalquantitiesoflinearrelationsinnormedspaces[J].QuaestionesMathematicae, 1994, 17: 487-498.

[11]ALVAREZT.Onalmostsemi-Fredholmlinearrelationsinnormedspaces[J].GlasgowMathematicalJournal, 2005, 47:187-193.

[12]BOASSOE.RegularFredholmpairs[J].OperatorTheory，2006, 55: 311-337.

[13] 范亚静. 关于正则Fredholm多值线性算子对 [J]. 应用泛函分析学报,2012, 14(3): 265-273.

(编 辑亢小玉)

A classification of regular Fredholm pairs of multi-valued linear operators

FAN Ya-jing1,2, JIAN Ren-yi1

(1.College of Mathematics and Information Science, Beifang University of Nationalities, Yinchuan 750021, China；2.School of Mathematics and Information Science, Shaanxi Normal University, Xi′an 710062， China)

classification; regular Fredholm pair; muti-valued linear operator

2014-05-11

国家自然科学基金资助项目(11371012)；北方民族大学校级基金资助项目(2012Y038)

范亚静,女,河北承德人，北方民族大学讲师,陕西师范大学博士生,从事算子代数与量子信息研究。

O177.1

：ADOI：10.16152/j.cnki.xdxbzr.2015-02-004