椭圆模型模拟声带振动的远场指向性

曹 辉,魏 静,赵海君

(陕西师范大学 物理学与信息技术学院/陕西省超声重点实验室, 陕西 西安 710119)



·信息科学·

椭圆模型模拟声带振动的远场指向性

曹 辉,魏 静,赵海君

(陕西师范大学 物理学与信息技术学院/陕西省超声重点实验室, 陕西 西安 710119)

针对声带振动产生的声场的空间分布问题,根据声带的生理结构、振动特性及声学基本理论知识,提出用椭圆振动模型来模拟声带的振动,采用点源组合的方法计算了正常声带模型振动时产生的远声场的指向性。运用Matlab对声带模型的声场指向性进行了模拟仿真与分析,讨论了声带振动频率对声带模型产生的指向性的影响以及振动的点源数对声压幅值的影响;并模拟出当声带发生病变时,会影响声带模型的声压幅值,进一步又探讨了声带模型空隙尺寸发生变化时声场指向性的变化规律。结果表明,与正常声带模型相比,病变声带模型已不再有原来的规律,从而为声带的进一步研究及临床治疗提供了理论基础。

声带;远声场指向性;声压幅值

随着社会的进步和社会交往的频繁,言语的表达在人们的工作和生活中扮演着不可或缺的角色,人们对嗓音质量和言语表达的要求也越来越高,而嗓音的产生需要有完善的发声或发音系统。声带是发生系统的核心器官和生理基础,声带又称声壁,是发声器官的主要组成部分,主要功能是振动以发声。它位于喉腔中部,由声带肌、声带韧带和黏膜3部分组成,左右对称。从肺部呼出的气流冲开闭合的声带,使其振动并发出声门波,通过发声器官的运动,可改变声带的位置,声带的张力以及声带的振动模式,从而发出不同的声音,这就成了我们所听到的各种话语声或歌声。基音是由喉部发出的,再经过共鸣腔的作用,使声音增强或发生变化,然后通过发音器官的协同作用产生不同的语音[1]。人类嗓音的基本特征在很大程度上由声带决定[2],声带病变或其他病因会影响声带的正常运动,因此研究声带的振动模型对揭示人类嗓音的基本特征和嗓音的生理病理性特征有着极其重要的意义。日常生活中嗓音疾病较为常见,为了更好地研究嗓音疾病的诊断和治疗,有必要对正常声带、病理性声带进行深入的研究。

本文根据声带的生理结构及振动特性,提出用椭圆振动模型来模拟声带的振动,假设各点源等角度的分布在椭圆上,在理论上计算了该振动模型所产生的远声场的指向性[3],进而研究了声带振动的远声场特性。

1 模型的建立与理论计算

根据人体正常与病变声带的实物图片[4](图1、2),可将此声带的等效模型建立为椭圆形状,为了便于计算,可认为椭圆模型是由很多点源组成,各点源等角度的分布在椭圆上。

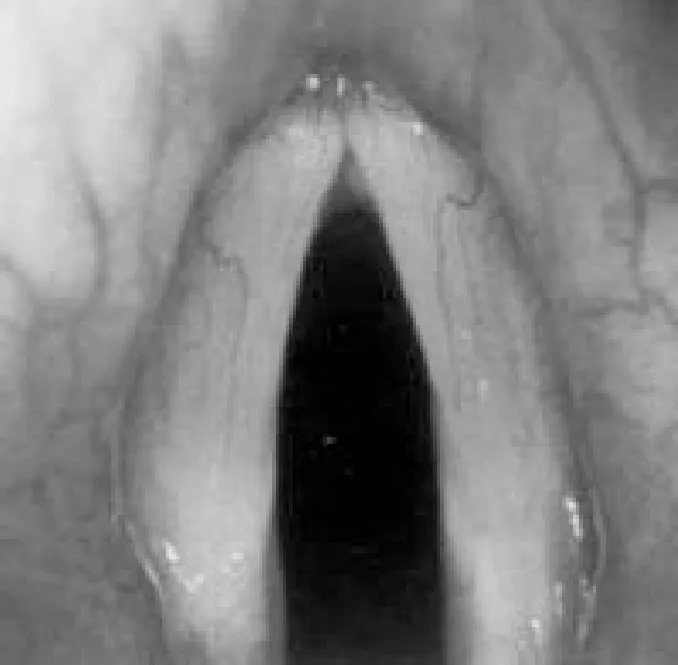
图1 人体正常声带的实物图Fig.1 Normal vocal cords diagram

图2 病变声带的实物图Fig.2 lesion vocal cords diagram

在此声带振动模型中,选取模型中心点o所在的位置为空间直角坐标系的原点,模型所在的平面为xoy平面,以椭圆的长轴和短轴所在的直线为x,y轴(如图3)。声场中的一点p与坐标原点o相距为r,p点的坐标为(xp,yp,zp),Qi(xi,yi,zi)为模型上的第i个小振元的坐标,iψ0是第i个点源Qi与x轴所成的角度,op与z轴的夹角为θ,坐标原点与p点投影Q的连线与x轴的夹角为ψ。

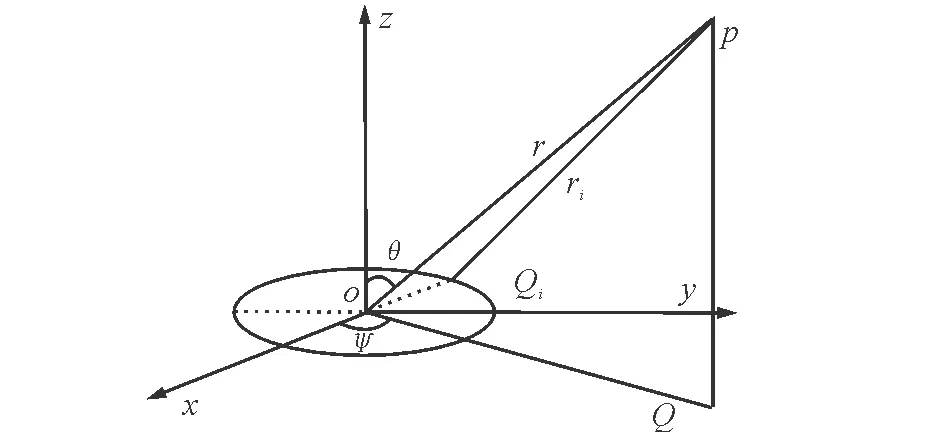
图3 声带模型的声压指向性计算原理图Fig.3 Schematic diagram of directivity calculation of vocal cords model

假设模型o处存在一小振元,则Qi处的振元的振动相对于o点处的振元的振动传到观察点p的声程差为

ξi=op-Qip=oQi.eop，

(1)

其中eop是op的单位矢量。

因为p点的各坐标分量可表示为

xp=rsinθcosψ,yp=rsinθsinψ，

zp=rcosθ。

(2)

则

(3)

即

eop=(sinθcosψ)i+(sinθsinψ)j+cosθk。

(4)

因此,ξi=xisinθcosψ+yisinθsinψ，

(5)

相对应的相位差为

(6)

对于椭圆,其方程为

(7)

如图3声带模型中,假设它有n个基元,分别分布在偏心角ψ0,2ψ0，…,iψ0，…处,根据式(7),可得其任意点Qi的坐标为

(8)

代入式(6)可得相位差εi为

εi=

(9)

假设模型o处的点声源在p点产生的声压为

(10)

其中A0为o处振元在距其r的空间一点产生的声压振幅。

为计算方便,设模型中各点源作同频率、同相位、等幅度简谐振动,并且与模型中心处的振元产生的相位、振幅完全相同,以模型o处的点声源在p点产生的声压为参考,则模型上的任一小振元Qi在p点产生的声压为

(11)

式中εi为模型中任一小振元相对于o处的点声源在p点因声程差ξi引起的相位差,ri是Qi到空间一点p的距离;因为|oQi|≪r,则ri≈r。

对于含有n个小振元的声带模型在远场p点产生的合成总声压,只要将每个小振元产生的声压叠加起来即可得到,则

(12)

(13)

式中A′为声波的总声压振幅,则

(14)

当θ=0时,即在声带模型的正上方,各振元辐射的声波在远场点同相位,故它们的合成声压达到最大值nAi。

那么该声带模型归一化的方向性函数为

(15)

即

(16)

2 理论分析和讨论

2.1 振动频率对指向性的影响

图4 不同频率下的声场指向性的变化规律图Fig.4 Rule of the sound field directivity at different frequency

由图4可知,声带模型在不同的频率下振动时,在θ从0～π之间变化的过程中,声压的变化与θ有关,并出现了一定的规律性,当θ=0，π时声压最大,声压随θ的增大出现先减小后增大的变化,在θ=π/2时声压最小;所不同的是当振动频率增大时,声压最小值越来越小。

2.2 振动的点源数对声压幅值的影响

当声带模型的长短轴分别为15 mm和1 mm,振动频率为500 Hz时,不同的振动点源数n影响了声带振动的声压幅值如图5所示(x轴为θ弧度,y轴为ψ弧度,z轴为空间各点的声压与其最大值的比值)

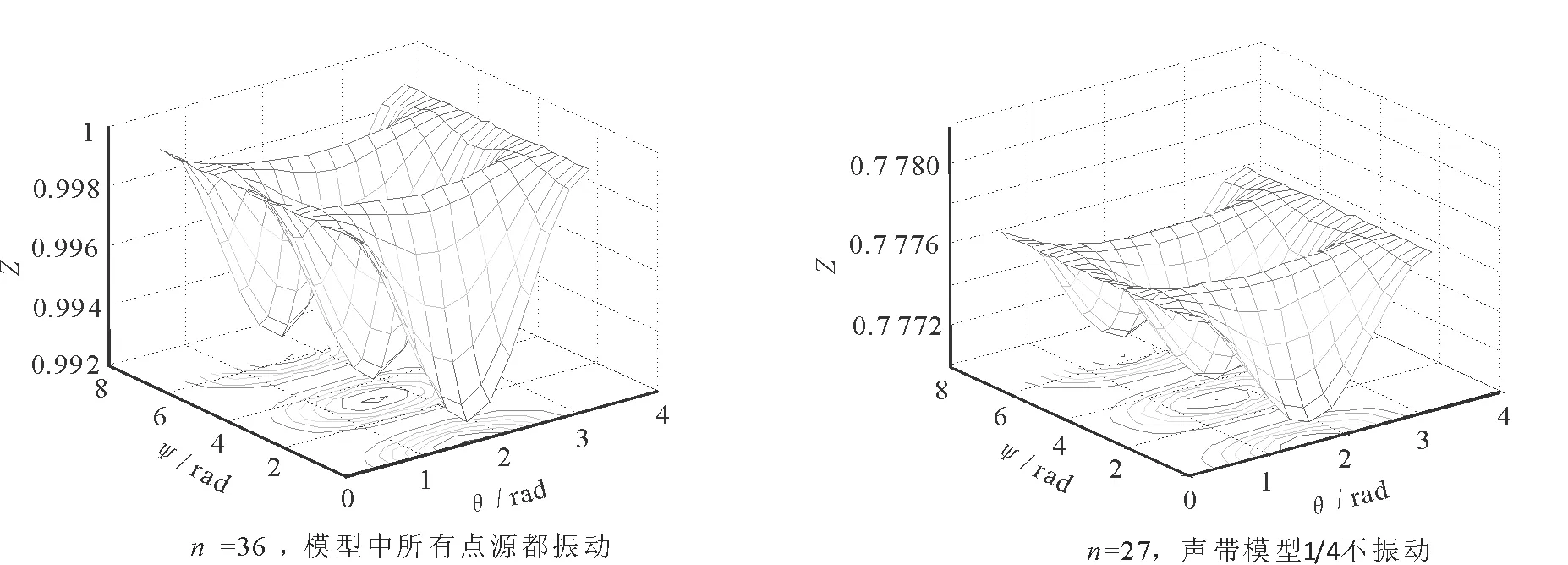
图5 不同的振动点源数n下的声压幅值的变化规律图Fig.5 Rule of the sound pressure at different point sources

由图5可知,当正常声带振动时,声压相对幅值最大;当声带发生病变时,随着振动的点源个数减少,声压相对幅值也会相应的降低。

图5中当声带发生病变时声带振动的幅值变小,说明声带的振动是不正常的,因而根据声压相对幅值变化的程度可以对人的声带健康程度进行评估。

2.3 声带模型孔隙尺寸对声场指向性的影响

因每个人声带的长度、松紧,张开的尺寸不同,所发出的声音也就不同,因此研究声带张开孔隙的大小对声场指向性的影响是很有必要的。为了研究孔隙的大小对指向性的影响,假设声带频率为500Hz,对于正常声带模型,实验所用的点源数为n=36(其他数目的点源有类似的结论),声带模型空隙尺寸发生变化时,指向性的变化规律(如图6，7)。

由图6可知，当此模型a,b的大小相差很大时,指向性图变化不明显,声压的最小值随着短轴的增大而变小。

由图7可知，当正常声带模型的短轴与长轴相差很小时,指向性图发生了较为明显的变化,并且当模型的短轴等于长轴时,对声压在xy平面的投影进行分析,可知若θ不变,声压的投影是一条直线,是等压线。说明声压的变化与ψ无关;并且随着声带模型短轴的增大,声压最小值越来越小。

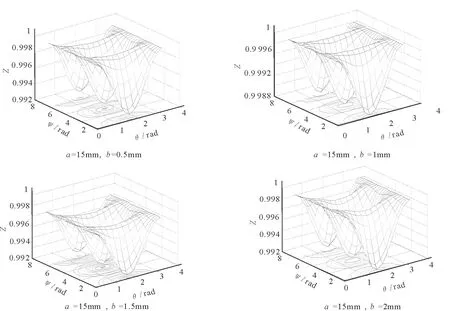
图6 不同的声带模型孔隙下的声场指向性的变化规律图Fig.6 Rule of the sound field directivity at different vocal pore

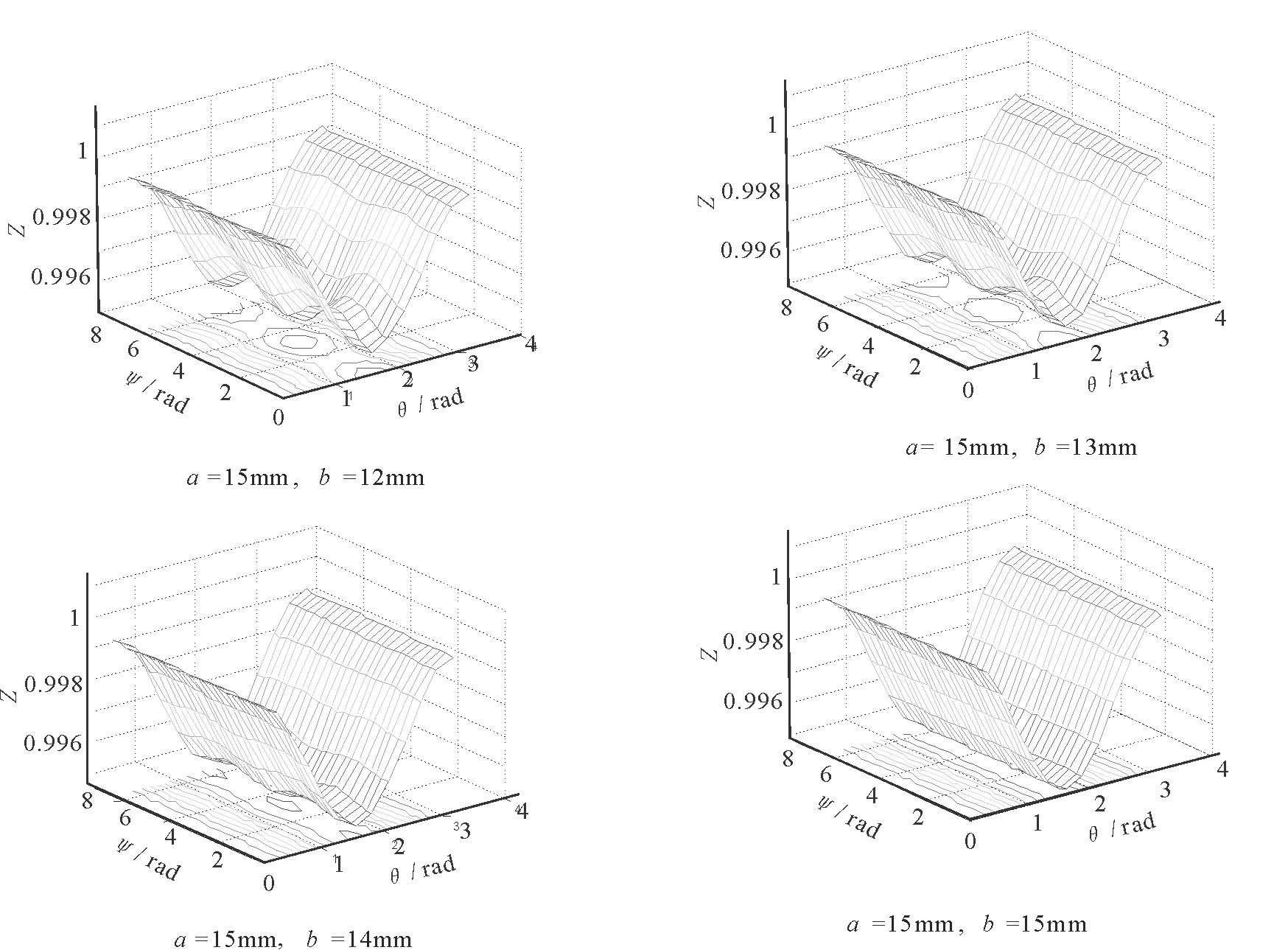
图7 不同的声带模型孔隙下的声场指向性的变化规律图Fig.7 Rule of the sound field directivity at different vocal pore

2.4 正常声带与病变声带对声场指向性的影响

在电声学中,声门可等效为一规则圆孔,即当a=b时,且声带频率为500Hz时,正常声带与病变声带对指向性的影响如图8所示。

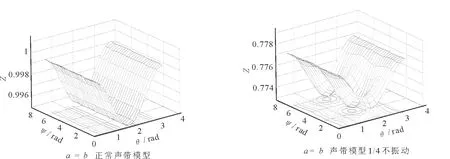
图8 正常声带与病变声带模型指向性变化规律图Fig.8 Rule of the sound field directivity produced by normal and lesion vocal cords

由图8可知，若声带发生病变,当声带模型的长轴等于短轴时,将其与健康人的正常声带振动产生的声场指向性变化规律相比较,声带模型产生的声场指向性发生了变化,已不再有原有的规律,进而对声带疾病的研究提供了理论基础。

3 结 语

本文用椭圆振动模型来模拟声带振动,将声带模型看成是多个点源的组合来描述声带振动在空间产生的辐射声压的指向特性。各点源等角度的分布在椭圆上形成椭圆点阵,根据声学基本理论,计算了该椭圆阵产生的声压指向性并进行了讨论。

经理论计算并运用Matlab进行仿真分析可知,声带振动的频率不同时,声压变化出现了一定的规律,声压随θ角度出现了先减小后增大的变化,且当振动频率增大时,声压最小值越来越小;而且声带振动所产生的声压幅值与模型中点源个数有关,即模型中n的取值会影响声带振动产生的声场的声压幅值,当声带的某处发生病变时,该模型中对应的点源也就不振动,从而影响了声带振动在远场处的产生的声压幅值;当声带孔隙尺寸发生变化时,声带模型的短轴和长轴相差不大时,声压的指向性也发生了变化,与病变声带相比,声带的振动失去了原有的规律,因而对声带的临床治疗有着极其重要的意义。

[1] CHILDERS D G, HICKS D M, MOORE G P, et al. A model for vocal fold vibratory motion,contact area,and the electro-glottogram [J].Acoustical Society of America,1986,80:1309-1320.

[2] 赵守国,孙义和,王素品. 基于复倒谱的声门下嗓音源研究[J]. 生物物理学报,2002,18(4):434-439.

[3] 杜功焕,朱哲明,龚秀芬.声学基础[M].南京:南京大学出版社,2001.

[4] 于萍,王荣光. 嗓音疾病与嗓音外科学[M]. 北京:人民军医出版社,2009.

[5] YANG An-xiong, LOHSCHELLER J, BERRY D A, et al.Biomechanical modeling of the three-dimensional aspects of human vocal fold dynamics[J].Acoustical Society of America Journal, 2010,127(2):1014-1031.

[6] DUPUCH V, SAROUL N, AUMERAN C, et al. Bilateral vocal cord abductor paralysis associated with primary herpes simplex infection:A case report[J]. European Annals of Otorhinolaryngology, Head and Neck Diseases,2012,129:272-274.

[7] 封子阳,曹辉,魏阿妮.声带振动产生的声场的远声场研究[J].压电与声光,2012,34(1):15-16.

[8] 周洪福.水声换能器及基阵[M].北京：国防工业出版社,1984:216.

[9] 魏春生,王薇,陈小玲.计算机图像处理技术对声门图像参数的检测及临床意义[J].临床耳鼻咽喉科杂志,2000,14(12)：540-541.

[10] 周林灿.病理噪音的声学分析和合成[D]. 上海:华东师范大学,2011.

[11] 胡巧.声带和室带病变的超声诊断进展[J].中国临床医学影像杂志,2010,8(21):566-568.

(编 辑曹大刚)

Research on far-field directivity of the elliptic model simulating vocal cord vibration

CAO Hui, WEI Jing, ZHAO Hai-jun

(School of Physics and Information Technology/Shaanxi Key Laboratory of Ultrasonics, Shaanxi Normal University， Xi′an 710119， China)

Aiming at the problem of the space sound field distribution generated by the vocal cord vibration, elliptic model simulating vocal cord vibration is put forward according to the physiological structure and vibration characteristics of the vocal cord and the basic theory of acoustic knowledge, the combination of point source is used to calculate far sound field directivity generated by the normal vocal cord vibration, simulating and analyzing sound field directivity of vocal fold model by using Matlab and discussing the impact of frequency on directivity and the impact of point source numbers on sound pressure amplitude of the vocal cord model; and it is simulated that the vocal cord lesions affects sound pressure amplitude of the vocal cord model, further more the vocal cord gap size impacting on sound field directivity is discussed. The results show that the lesion model no longer has primary rules than the model of normal vocal cord, which provides a theoretical basis for further study and clinical treatment of vocal cord.

vocal cord; far sound field directivity; sound pressure amplitude

2014-04-11

国家自然科学基金资助项目(11374199)

曹辉，男，重庆人，陕西师范大学副教授，博士，从事语音声学研究。

R767.92

：ADOI：10.16152/j.cnki.xdxbzr.2015-02-010