关于相对拓扑压的一个注记

张 强,历智明

(西北大学 数学学院, 陕西 西安 710127)



·数理科学·

关于相对拓扑压的一个注记

(西北大学 数学学院, 陕西 西安 710127)

通过引入映射的基的概念,运用分离集在非紧系统中定义并研究了相对拓扑压,给出了相对拓扑压的若干基本性质,并且证明了相对拓扑压是一致拓扑共轭下的不变量。

映射的基;非紧系统;相对拓扑压;一致拓扑共轭

在拓扑动力系统的研究中,拓扑熵是一个非常重要的拓扑共轭不变量,反映了拓扑动力系统的复杂程度。拓扑熵这一概念首先是由Adler,Konheim和McAndrew[1]于1965年运用开覆盖的方法引进的。随后, Bowen[2]和Dinaburg[3]于1971年在度量空间中运用张成集和分离集给出了拓扑熵的另外一种新的定义,并且证明了在度量空间是紧空间的情形下,这两种定义是等价的。

拓扑压作为拓扑熵概念的一种推广,它首先是由Ruelle[4]于1973年在扩张动力系统中引进的。随后,Walters[5]于1975年把这个概念延伸到了一般的连续函数情形,并且系统地介绍了关于拓扑熵和拓扑压的一些基本概念和性质。与拓扑压、变分原理及平衡态有关的理论在统计力学、遍历理论和动力系统的研究中扮演了一个十分重要的角色。由于Bowen[6]和Ruelle[7]的工作,拓扑压已成为动力系统中维数理论研究的一个基本工具。

但前人的工作大都局限在对于紧致系统的研究。为了在非紧系统中给出拓扑熵和拓扑压的合理定义,2008年,M. Malziri和M.R. Molaei[8]通过引入映射的基的概念在非紧系统中给出了拓扑熵概念的一个推广。另外,在许多工程问题中,我们研究一种自然现象常常需要考察许多数据。然而,由于观测者观测角度的不同，实际上往往得到的是一些近似值。因此,为使得到的研究结果符合实际情况,需要考虑观测者的角度。当我们通过把观测者的角度添加到拓扑压的概念中时，实际上就为观测者建立了一个数学模型,这对我们科学的考察实际问题当然是大有裨益的。 基于此,2010年,M.R. Molaei和H. Molaei[9]通过映射的基运用张成集把观测者的角度添加到了拓扑压的概念中去,他们在非紧系统中运用张成集定义并研究了相对拓扑压,同时还给出了相对拓扑压的若干基本性质。

本文通过对文献[9]运用张成集所定义的相对拓扑压的研究,首先运用分离集给出了相对拓扑压的另外一种新的定义方式,继而研究了这两种定义方式在一定条件下的等价性,随后系统而深入地研究了相对拓扑压的若干基本性质,最后给出了一致拓扑共轭的两个系统之间的相对拓扑压的关系。

1 基本定义和概念

本文记N为全体正整数集,R为全体实数集。

1.1 相对拓扑动力系统

为了克服系统的非紧性带来的困难,我们需要在下面的动力系统中引入映射的基的概念,从而在非紧系统中给出拓扑熵和拓扑压的合理定义。

定义1[8]设(X,d)是一个度量空间(无需紧致),K是X的一个紧子集,f:X→X是X上的一个连续自映射。若对X的任意一个紧子集C,总存在m(C)∈N,使得对任意的n≥m(C),都有fn(K)⊇C,则称K是f的一个基,记作(f,K)。

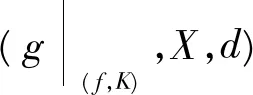
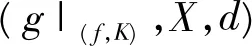
由文献[9],有

据此,给出下述一个定义。

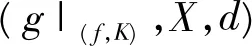
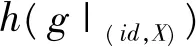
1.2 相对拓扑压的张成集定义

文献[9]运用张成集所定义的相对拓扑压为：

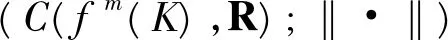
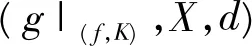
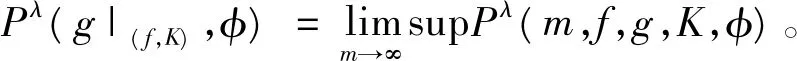
2 用分离集定义相对拓扑压

由定义2可以看出,用张成集和分离集所定义的相对拓扑熵是等价的。另外,文献[9]运用张成集给出了相对拓扑压的定义。现在一个很自然的问题是:我们能否运用分离集给出相对拓扑压的定义,并且该定义与文献[9]用张成集所定义的相对拓扑压是否等价?

2.1 用分离集定义相对拓扑压

下面的符号同第2节。

则E0也是fm(K)的一个(m,n,g,ε)-张成集.

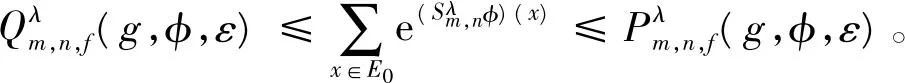
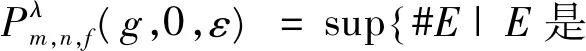
则根据定理1,有下述一个推论。

推论1 对任意给定的m∈N,ε>0及φ∈C(fm(K),R),有

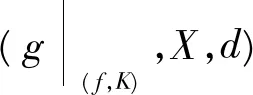
证 明 第1步,证明:

据此,有

又因为

λ(gi(x))φ(gi(x)))≥

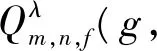
由此有

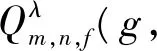
于是有

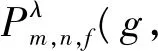
因而

(1)

第2步,证明:

由推论1的第(2)条,有

(2)

又由式(1)知,对任给的δ>0,有

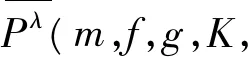
于是有

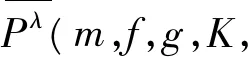
(3)

注3 该定理是对紧度量空间中拓扑压两种等价定义的一种推广。

3 相对拓扑压的基本性质

在给出相对拓扑压的基本性质之前，首先给出下述一个引理。

引理1[10]

2)设{aj},{bj}是两个正实数集,则

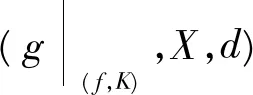
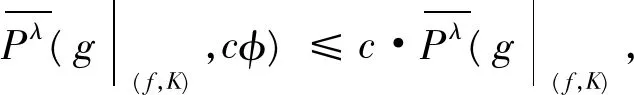
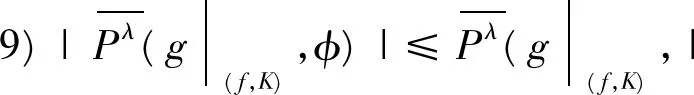
证 明 定理3中的2),3),6),7),8),9)与文献[9]中的证明方法类似,这里从略。下面我们对定理3中的1),4),5)给出证明。

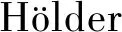
由此有

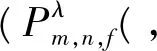
于是有

Pλ(m,f,g,pφ+(1-p)ψ,ε)≤

p·Pλ(m,f,g,φ,ε)+(1-p)·

Pλ(m,f,g,ψ,ε)，

于是有

由此有

故

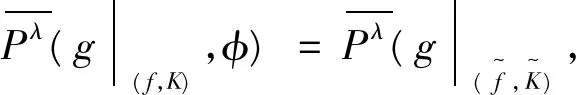
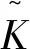
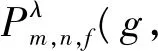
由此有

于是有

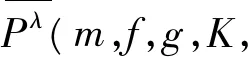
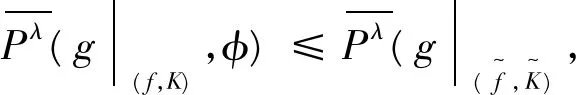
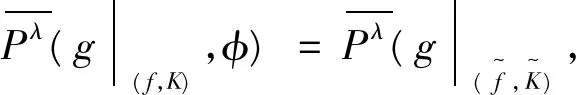
4 一致拓扑共轭

我们给出一致拓扑共轭的两个系统之间的相对拓扑压的关系之前，首先给出下述一个定义。

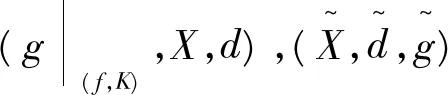
因而hn(π(K))=(π∘fn∘π-1)(π(K))=π(fn(K))⊇C。

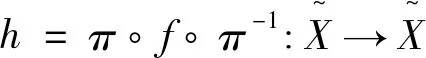
这里,不妨取δ≤ε。

因而

据此,有

由此有

于是有

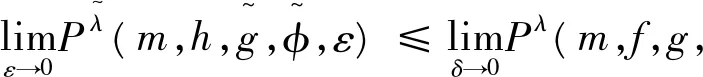
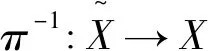
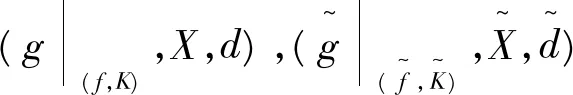
证 明 根据定理5,有

根据定理6,有

故

[1]ADLERRL,KONHEIMAG，MCANDREWMH.Topologicalentropy[J].TransAmerMathSoc, 1965(114): 309-319.

[2]BOWENR.Entropyforgroupendomorphismsandhomogeneousspaces[J].TransAmerMathSoc, 1971(153):401-414.

[3]DINABURGEI.Aconnectionbetweenvariousentropycharacterizationsofdynamicalsystems[J].IzvestijaANSSSR, 1971(35):324-366.

[4]RUELLED.StatisticalmechanicsonacompactsetwithΖvactionsatisfyingExpansivenessandspecification[J].TransAmerMathSoc, 1973(187): 237-251.

[5]WALTERSP.AvariationalprincipleforthepressureofContinuousTransforma-tions[J].AmerJMath, 1975(97): 937-971.

[6]BOWENR.Hausdorffdimensionofquasicircles[J].InstitutdesHautesEtudesScientifiques,1979(50): 11-25.

[7]RUELLED.Repellersforrealanalyticmaps[J].ErgodicTheoryandDynamicalSystems, 1982(2): 99-107.

[8]MALZIRIM,MOLAEIMR.Anextensionofthenotionoftopologicalentropy[J].ChaosSolitonsandFractals，2008(36): 370-373.

[9]MOLAEIMR,MOLAEIH.Relativetopologicalpressure[J].MathematicalReports，2010(1): 31-36.

[10]WALTERSP.AnIntroductiontoErgodicTheory[M].Berlin:Springer-Verlag，1982.

(编 辑亢小玉)

A note on relative topological pressure

ZHANG Qiang, LI Zhi-ming, WANG Yan-geng

(School of Mathematics, Northwest University, Xi′an 710127， China)

The relative topological pressure is defined by separated set in non-compast system via the notion of the base of a map. In this paper, the basic properties of relative toplogical pressure are obtained, and the relative topological pressure is proved as an invariant with respect to uniformly topological conjugation.

base of a map; non-compact system; relative topological pressure; uniformly topological conjugation

2013-11-18

国家自然科学基金资助项目(11301417,11371292)

张强,男,陕西宝鸡人,从事拓扑动力系统的研究。

O29

：ADOI：10.16152/j.cnki.xdxbzr.2015-02-003