一种GNSS大网数据快速高效处理策略

崔 阳 吕志平 张友阳 陈正生 李林阳

1 信息工程大学地理空间信息学院，郑州市科学大道62号，450001

2 郑州轻工业学院机电工程学院，郑州市东风路5号，450002

目前，GNSS数据的主要处理方法是双差网解和非差精密单点定位（PPP）［1－2］。PPP 的处理时间呈线性增加，而双差网解的处理时间呈几何倍数增加，当测站规模增加时，两种处理策略都因计算能力有限而无法高效处理［3－5］。陈俊平等［6］建议增加数据采样间隔以实现GNSS 的非差数据处理。程传录等［7］提出移动格网密度法，以优化GAMIT 软件划分子网算法的局限性。从解算精度上比较，PPP解算结果和双差网解精度基本一致［8］，但精密单点定位的东向精度仍然可以通过整周模糊度的固定得到提高，使解算结果接近全网解算结果。为了提高PPP 的精确性和准确性，可联合PPP 解算结果，进行双差载波相位模糊度固定解算［9－10］。因此，基于PPP模式的网解是大型GNSS 网络数据处理发展的必然趋势。然而，全网模糊度解算的处理时间接近O（n4），限制了网络测站数目，只能以小网模式固定模糊度。Blewitt［10，11］2008年提出“不动点 定理”的模糊度固定方法，并基于此提出了Ambizap 算法，该算法的处理时间接近O（n），解算结果近似于全网模糊度的固定。随着分布式网络计算平台的出现，利用网络中多台计算机建立分布式计算系统平台成为解决大规模测量数据计算问题的首选方法［12－13］。本文基于分布式计算理论，将Ambizap算法应用到大型GNSS 网数据分布式处理中。算例表明，Ambizap的分布式应用为大型GNSS数据处理带来一种经济快捷的新方法。

1 Ambizap算法原理

Blewitt［11］在2008年基于不动点理论提出Ambizap算法，该算法利用双差模糊度解算结果来约束非差PPP解。

1.1 不动点理论

“不动点理论”可以描述为：在特定条件下，运算符F（x）将至少有一个不动点满足F（x）＝x条件。不动点理论需要说明不动点是什么或者如何找到它们。将F定义为模糊度固定运算符，即利用双差模糊度解算结果去约束每站的PPP解，以修正非差解，进而更新其他相关参数。通过寻找一个固定点去映射从初始PPP估值参数到模糊度固定后的参数。由于参数集都可以转变为另一等价形式（完全线性无关的），则假设对任意值的参数s，有线性变换且满足。网中存在这样的固定点，代表网中加权平均质心点。

1.1.1 不动点定理1：质心

假设对n个独立测站的PPP单站解，设其解的向量为si，方差－协方差为Ci，i∈（1，…，n）。令向量si包含测站三维坐标分量和所有卫星的载波相位的星间差。定义偏差固定运算符F（Λs）为从初始PPP 解算的参数估值的任意线性组合映射到偏差固定解，第一个不动点理论可表述为：

1.1.2 不动点定理2：基线

网平差的初始信息由每站PPP解提供，网中的一个单一基线解将产生两个模糊度固定的解向量s′i和s′j，其中均包含测站坐标和模糊度。假设协方差是相似的，将偏差固定运算符F应用到整个网中，得到不动点定理2：

每个模糊度固定后的基线的参数与网内其他模糊度固定的基线是不相关的［5］。

1.2 基于双差固定解约束PPP解的整网平差

设整网平差前PPP 实数解为Xi，协方差矩阵为Ci，测站i和j构成的独立基线的双差固定解为X′i和X′j，将各个独立基线的双差固定解当作独立的子网。对于连续观测的大型GPS网络，实践表明，各站的非差PPP 解的精度、双差模糊度固定解的精度均相近，则根据Blewitt提出的不动点定理，可利用双差模糊度固定解对PPP解进行精度修正，得到整体网平差解。由不动点定理1和2假设［2，14］：

1）整网平差前的测站PPP解Xi的加权平均和整网平差后的测站坐标相等（整网平差的位置基准）；

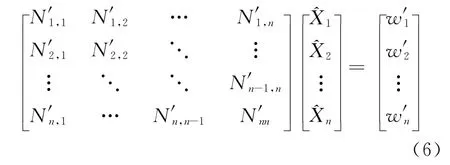
2）整网平差前的双差基线ΔX′i⊗j＝X′i－X′j与整网平差后的坐标反算的基线向量相等（整网平差的方位基准和尺度基准）。设单个测站的非差法方差为NiXi＝wi，根据测站之间相互独立的原则，构建PPP网解的法方程：

引入独立基线的双差固定解提供的约束条件：

其中，双差基线ΔX′i⊗j的协方差阵为C′i⊗j，i⊗j表示由测站i和j构成的独立基线。独立基线的双差固定解ΔX′i⊗j提供给测站i和j的PPP解的精度改进为：

式中，C′i⊗j为双差基线ΔX′i⊗j解的方差－协方差阵；Ci和Cj是测站i和j的非差PPP解方差－协方差矩阵；Ai⊗j为改进后的测站i和j的方差－协方差阵；ε为一个很小的实数，避免了双差固定解不能给PPP 解提供精度改正信息而导致矩阵求逆病态，一般取ε＝10－4。将独立基线引入的约束条件并行累加到非差PPP网解法方程，得到新整网平差的法方程：

1.3 独立基线选择

不动点定理的应用需逐条基线进行双差模糊度的固定，对于测站数为n的同步观测网，函数不相关的独立基线数共有n－1条。理论上，所有双差模糊度都可表示为独立双差模糊度的线性组合，在数理统计上是等价的，但独立基线的不同选择会导致模糊度最近整周偏差不同以及方差不同，从而影响模糊度固定的效率。一般情况下，不动点理论可采取模糊度更容易固定的最短基线法构建独立基线网。本文首先采用Delaunay三角网剖分算法对GPS网进行三角剖分，然后采用图论中的欧几里德最小生成树（EMST）算法实现独立基线网的构建，保证所有独立基线边的总长度最小。其中，考虑到当前基准站数目在几千个点以内，剖分时间占计算时间的比例很小，Delaunay三角网剖分算法采用逐点插入法；最小生成树算法就是用于求解带权无向连通图中最小生成树的算法，常见的有Kruskal算法、Prim 算法和Sollin算法等。

2 Ambizap算法的分布式处理

为充分利用多核多机的分布式网络计算环境，对大型GNSS网数据，可通过分布式PPP 解算和分布式独立基线解算完成Ambizap算法的分布实现，从而实现大型GNSS网数据分布式高效处理。图1为按照不动点理论设计并编程实现的GNSS数据分布式计算流程。

在图1中，首先是采用解压工具、TEQC等对各测站数据进行分布式预处理，然后调用PPP模块将测站分布并行PPP处理，根据独立基线的选择情况，再进行并行基线解算，最后将独立基线解算结果约束到PPP解算结果上，进行整网平差计算。

在具体流程实现中，首先根据测站列表建立PPP任务，控制端根据任务列表发布PPP计算任务，网络中可用计算节点并行完成PPP计算任务后，将计算结果返回给控制端或指定的网络位置。然后，控制端对测站进行三角剖分并建立三角网列表和基线向量列表，从基线向量列表中按照最短路径原则选择n－1条独立基线建立独立基线任务，控制端分发独立基线任务给网络中可用计算节点，当所有计算节点完成计算任务后，控制端统计所有独立基线模糊度解算成功情况，针对计算失败的独立基线，根据索引编号查找所属三角网，重新选择替代基线，再对替代的基线进行任务建立和任务分发与计算，直到完成所有n－1条独立基线计算任务。相关GNSS 数据处理模块通过调用封装已有的商用软件（Bernese等）或开源代码（GPSTk等）模块实现。

图1 基于Ambizap算法的GNSS数据分布式计算流程Fig.1 Flowchart of GNSS data in a distributed Ambizap algorithm

3 算例分析

3.1 算例1

选用欧洲AJAC等23个IGS跟踪站2002年第143天的30s采样间隔的观测数据，比较PPP解、基于Ambizap算法的网解与全网双差解的差异。

试验硬件平台为普通组装台式机，Intel Core i3－2100处理器，3.10GHz主频，4GB内存，Windows XP操作系统。在Visual Studio 2010环境下，采用C＃语言实现Ambizap 算法。相关的PPP解算和双差基线解算采用伯尔尼大学推出的高精度GNSS数据处理软件Bernese5.0版本，在Windows平台下，利用如下CMD 命令即可实现无交互的后台调用Bern的BPE：

Ambizap算法的实现过程是：首选调用BPE中的PPP模块进行PPP 解算，然后对测站进行Delaunay三角剖分，进而利用Kruskal算法生成测站的最小生成树，获得最短基线的独立基线，对每条独立基线调用BPE 中的RNX2SNX 模块进行单基线解算，最后实现带有双差约束的PPP解的整网并行平差，改正测站的非差PPP解。作为对比，调用RNX2SNX 模块对23 个测站同时进行全网双差解算。PPP 解与全网双差解的坐标差统计如图2所示。

图2 全网双差解与PPP解坐标差统计Fig.2 Coordinate difference statistics between double difference solution and PPP solution

由图2可知，PPP 解与全网双差解的坐标较差在X和Z方向在1cm 以内，但在Y方向（E向）达到2cm。Ambizap网解与全网双差解的坐标差统计如图3所示。

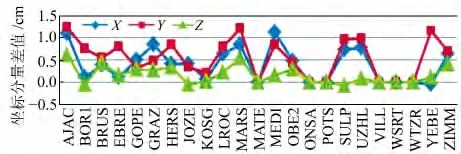
图3 全网双差解与Ambizap网解坐标差统计Fig.3 Coordinate difference statistics between double difference solution and Ambizap solution

由图3可知，Ambizap网解坐标与全网双差解坐标的较差多在1cm 以内，相比PPP 解得到改进，尤其是Y方向和Z坐标的改进效果明显。

3.2 算例2

为验证Ambizap算法分布式计算的高效性，搭建局域网分布式计算环境，针对不同规模的IGS站数据，采用基于Ambizap算法建立的分布式GNSS软件平台与GAMIT 软件平台分别进行处理。其中，方案1利用GAMIT 软件采用双差模式进行集中式处理；方案2利用分布式软件平台进行Ambizap算法的分布式处理。为了描述并行计算的性能，一般采用加速比指标进行度量。加速比定义为：

其中，n表示处理器个数，T1是改进前整个任务的执行时间，Tn是改进后n个节点并行执行时间。分别对IGS站2013年第1天的50、99和327个测站规模的观测数据进行处理，数据存放在指定的FTP服务端。采用上述两种方案进行处理，对比计算时间。测试过程中，分布式GNSS平台启用局域网中4台计算机组成分布式计算环境，其中一台兼任控制端。计算机均为配置相当的普通计算机，CPU2.2～2.4GHz，内存2～4GB。

由表1可知，50个测站时，分布式GNSS 平台比GAMIT平台提高2.82 倍；99个测站时，GAMIT 呈几何倍数增长，而分布式平台呈线性增长，且加速比达到9.40倍。现有GAMIT 平台无法同时处理327 个测站，而分布式平台能在243min内完成该计算任务。由于分布式算法和计算平台具有良好的伸缩性、扩展性和自动化效果，使用更多的计算节点时，计算效率将更高。

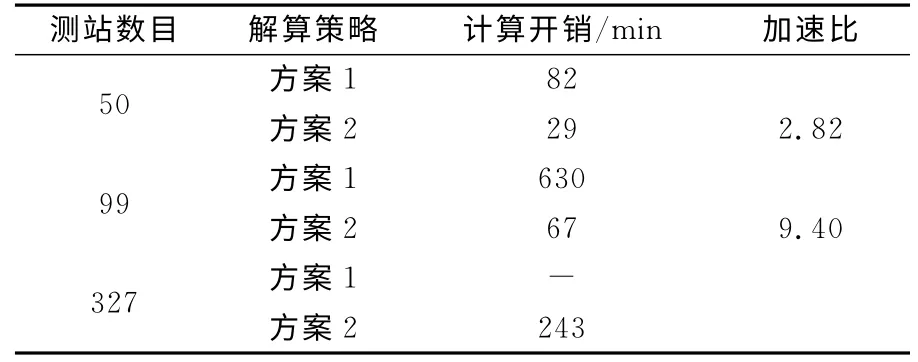
表1 计算时间的对比Tab.1 Comparison of the calculation time

4 结 语

本文基于Ambizap网解新算法的基本原理，提出通过利用分布式独立基线的双差固定解约束分布式的PPP解，进而进行整网并行计算的新方法，建立了具有良好分布特征的O（n）处理时间的整网分布式处理流程；利用.NET 框架下的分布式计算技术实现了Ambizap算法整网计算的分布式处理。通过算例验证了Ambizap 算法精度的可靠性和分布式处理的高效性，为大型GNSS网络数据的快速处理提供了一条高效、经济的新途径。

［1］Ge M，Gendt G，Dick G，et al.A New Data Processing Strategy for Huge GNSS Global Networks［J］.Journal of Geodesy，2006，80：199－203

［2］蔡华.GNSS大网实时数据快速解算方法应用研究［D］.武汉：武汉大学，2010（Cai Hua.Application Research of Method of Large GNSS Network Realtime Data Rapid Solution［D］.Wuhan：Wuhan University，2010）

［3］Dong D，Fang P，Bock Y，et al.Anatomy of Apparent Seasonal Variations from GPS－Derived Site Position Time Series［J］.Journal of Geophysical Research，2002，107（B4）：2 075

［4］Herring T.Aspects of Large Station Networks for GPS Orbits and Clocks［C］.IGS Workshop and Symposium，Switzerland，2004

［5］Blewitt G.Fixed Point Theorems of GPS Carrier Phase Ambiguity Resolution and Their Application to Massive Network Processing：Ambizap［J］.Journal of Geophysical Research，2008，113：B12 410

［6］陈俊平，张益泽，谢益炳，等.超大观测网络及多GNSS系统的快速数据处理［J］.武汉大学学报：信息科学版，2014，39（3）：253－257（Chen Junping，Zhang Yize，Xie Yibing，et al.Rapid Data Processing of Huge Networks and Multi－GNSS Constellation［J］.Geomatics and Information Science of Wuhan University，2014，39（3）：253－257）

［7］程传录，蒋光伟，聂建亮，等.利用双差的超大GNSS基准站网解算法改进［J］.武汉大学学报：信息科学版，2014，39（5）：596－599（Cheng Chuanlu，Jiang Guangwei，Nie Jianliang，et al.Improving the Processing Strategy Based on Double－Differenced Observations for Huge GNSS Network［J］.Geomatics and Information Science of Wuhan University，2014，39（5）：596－599）

［8］陈永奇，刘焱雄，王晓亚，等.香港实时GPS水汽检测系统的若干关键技术［J］.测绘 学报，2007，36（1）：9－12（Chen Yongqi，Liu Yanxiong，Wang Xiaoya，et al.GPS Real－Time Estimation of Precipitable Water Vapor－Hong Kong Experiences［J］.Acta Geodaetica et Cartographica Sinica，2007，36（1）：9－12）

［9］Zumberge J F，Jefferson D C.Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks［J］.Journal of Geophysical Research，1997，102：5 005－5 017

［10］Blewitt G，Hammond W，Kreemer C，et al.From Yucca Mountain Local Stability to Global Quaking：GPS Point Positioning Strategies Spanning the Spatio－Temopral Spectrum［C］.Advances in GPS Data Processing and Modeling for Geodynamics，London，2005

［11］Blewitt G.The Fixed Point Theorem of Ambiguity Resolution for Precise Point Positioning of GPS Networks：Theory and Application［C］.2006 AGU Fall Meeting，San Francisco，USA，2006

［12］Boomkamp H.Global GPS Reference Frame Solutions of Unlimited Size［J］.Advances in Space Research，2010，46：136－143

［13］Serpelloni E，Casula G，Galvani A，et al.Data Analysis of Permanent GPS Networks in Italy and Surrounding Regions：Application of a Distributed Processing Approach［J］.Annals of Geophysics，2006，49（4／5）：897－928

［14］陈宪冬.Ambizap方法在大规模GPS网处理中的应用及结果分析［J］.武汉大学学报：信息科学版，2011，36（1）：10－13（Chen Xiandong.Application of Ambizap Algorithm in Large GPS Network and Its Test Results［J］.Geomatics and Information Science of Wuhan University，2011，36（1）：10－13）