几种卫星钟差预报模型预报效果的分析与比较
王宇谱 吕志平 宫晓春 周海涛 王 宁
1 信息工程大学地理空间信息学院,郑州市科学大道62号,450001
卫星导航系统中,星载原子钟的钟差预报有着重要的作用[1-4]。钟差预报模型主要包括二次多项式(QP)模型[4-5]、灰色模型(GM(1,1))[5]、谱分析(SA)模型[6-8]、时间序列(ARIMA)模型[9,10]、Kalman 滤波(KF)模型[2,11]及其改进模型[12-14]等。本文使用IGS提供的精密钟差数据,从不同建模钟差数据量进行相同时间段钟差预报的角度,利用5种常用钟差模型对目前在轨运行的6种GPS卫星钟进行1、15、60d的钟差预报,根据预报结果对各模型的预报效果进行分析和比较。
1 预报试验与结果分析
使用GPS系统15min采样间隔的最终精密钟差产品进行预报试验。以GPS Week 17 464~17 576(2013-06-27~2013-09-14)共80d的钟差数据为例,同时考虑此时间段的星载原子钟包 括BLOCK ⅡA铯钟、BLOCK ⅡA铷钟、BLOCK ⅡR铷钟、BLOCK ⅡR-M铷钟、BLOCK ⅡF铯钟、BLOCK ⅡF铷钟6种类型,随机选取该时间段内不存在钟差跳变和间断、数据完整的每类钟的一颗卫星进行试验。文中选取PRN01、PRN10、PRN22、PRN24、PRN29、PRN32六颗卫星。预报试验中,以对应的IGS精密钟差数据作为参考真值,使用均方根误差(RMS)和极差(最大误差与最小误差之差的绝对值,记为Range)作为统计量,分析各模型的预报效果。其中均方根误差的计算公式为:

式中,errori为预报误差,是i时 刻IGS精密钟差值,ti为i时刻钟差预报值。
对于5种常用钟差预报模型,有以下3点需要说明:
1)本文SA 模型确定的过程为[6]:首先,利用二次多项式对已知钟差数据进行拟合得到拟合残差;然后,使用Daubechies小波进行信号分解并对残差进行降噪处理;接下来,采用傅里叶变换将降噪后的信号从时域变换到频域中,则信号分解为多个简单的正弦和余弦信号的叠加;最后,根据最大功率谱的量级,确定周期函数的阶数及其功率谱对应的频率。
2)本文使用ARIMA 模型进行钟差预报建模时,首先根据自相关函数和偏相关函数的截尾性初步确定模型和模型的阶数[9]。在模型确定后,利用AIC准则准确地确定模型的阶数[10],并通过最小二乘估计方法[9]求解模型参数。
3)本文使用基于方差递推法来确定噪声矩阵的KF模型进行钟差预报[4]。
最后,设计两种方案对各模型的钟差预报效果进行分析说明。方案一,使用2013-07-03的钟差数据进行建模,预报接下来1d(代表短期预报)、15d(代表中期预报)、60d(代表长期预报)。方案二,使用2013-06-27~07-03共7d的钟差数据进行建模,预报接下来1、15、60d的钟差。两方案中各卫星的钟差预报结果统计见表1~6(单位:ns)。
1)分析6个表中QP模型对应列的统计数据可以看出:①从表1、4可知,对于1d以内的短期预报,QP模型能够通过对历史钟差数据的有效拟合来反映钟差的变化规律,从而得到较好的预报结果:预报精度在亚ns到几个ns之间,预报稳定性对于铷钟在数个ns之内,而铯钟在几个ns到数十ns之间。而在中长期预报中,随着预报时间的增加,由于预报结果误差的不断累积,该模型预报结果的精度和稳定性迅速下降。因此,不宜采用该模型进行钟差的中长期预报。②由各表中6颗卫星的预报结果统计值可知,QP模型进行钟差预报时,其精度和稳定性随着星载原子钟种类的不同而变化。
2)分析6个表中SA 模型对应列的统计数据可以看出:①由于SA 模型较好地拟合了星载原子钟的周期项部分,因此,整体上使用SA 模型进行钟差预报能够得到较QP 模型更好的预报结果,预报精度和预报结果的稳定性均有一定程度的提高。而从表1~3中PRN10和PRN29的预报结果统计发现,此时QP 模型的预报效果均优于SA 模型的预报效果,说明在建模钟差数据相对较少的情况下,该模型还存在周期确定不准而导致预报效果不如QP 模型的现象。同时,在钟差的短期预报中,其预报结果的精度、稳定性与QP模型相当。长期预报中由于受到二次多项式主项的影响,随着预报时间的增加,模型的预报误差迅速增加,但预报效果优于QP 模型。②由各表中6颗卫星的预报结果统计可知,该模型进行钟差预报时,其精度和稳定性随着星载原子钟的不同而变化。
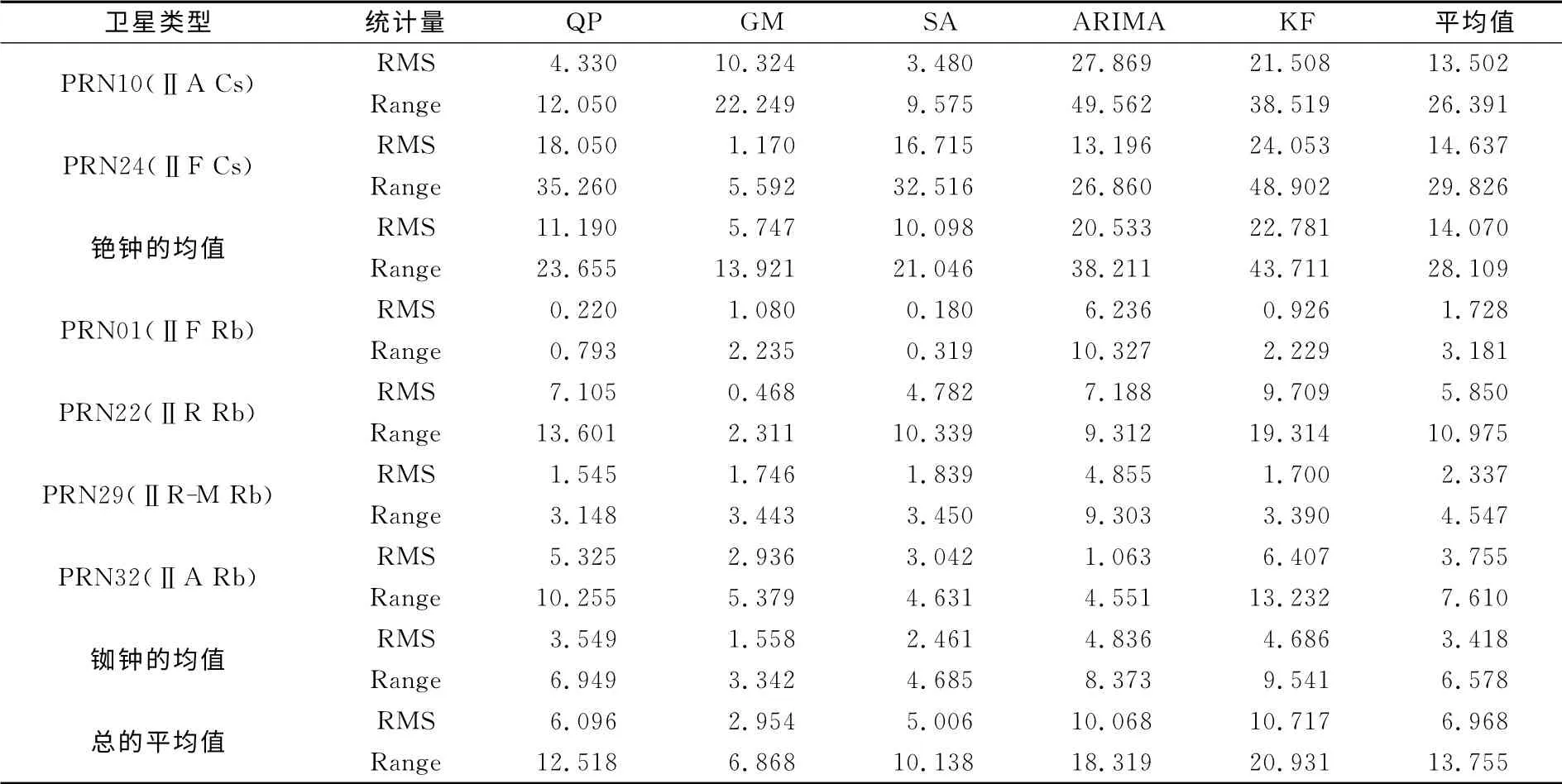
表1 方案一中5种模型1d预报结果的统计Tab.1 Statistics of prediction results for five models in 1day on the case ones
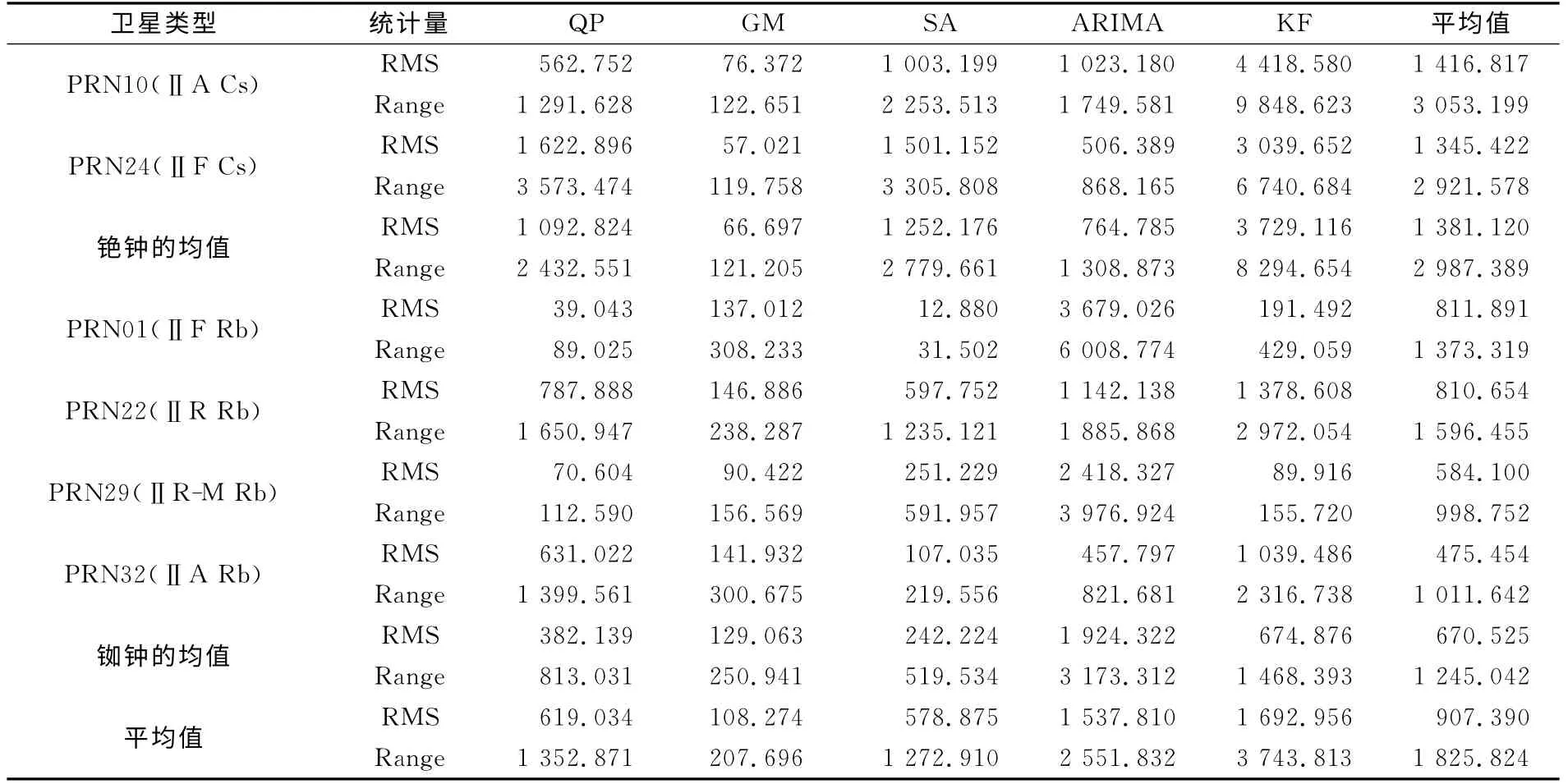
表2 方案一中5种模型15d预报结果的统计Tab.2 Statistics of prediction results for five models in 15day on the case one

表3 方案一中5种模型60d预报结果的统计Tab.3 Statistics of prediction results for five models in 60day on the case one

表4 方案二中5种模型1d预报结果的统计Tab.4 Statistics of prediction results for five models in 1day on the case two
3)分析6个表中GM(1,1)模型对应列的统计数据可以看出:①与其他4 种模型相比,GM(1,1)模型较为显著的特点是整体上对于钟差的中长期预报其预报效果较好,随着预报时间的增加其预报误差的增长较为缓慢,但预报有时会出现较大的误差,例如表3、6中PRN01卫星的长期预报。同时可以看出,GM(1,1)模型在使用试验所给时间段的钟差数据时,其短期预报结果的精度和稳定性与QP 模型和SA 模型相当。所以,GM(1,1)模型不但可用于钟差的短期预报,而且比较适合用来进行钟差的中长期预报。②由各表中6颗卫星的预报结果统计可知,该模型进行钟差预报时,钟差预报结果的精度和稳定性随着星载原子钟的不同而不同。
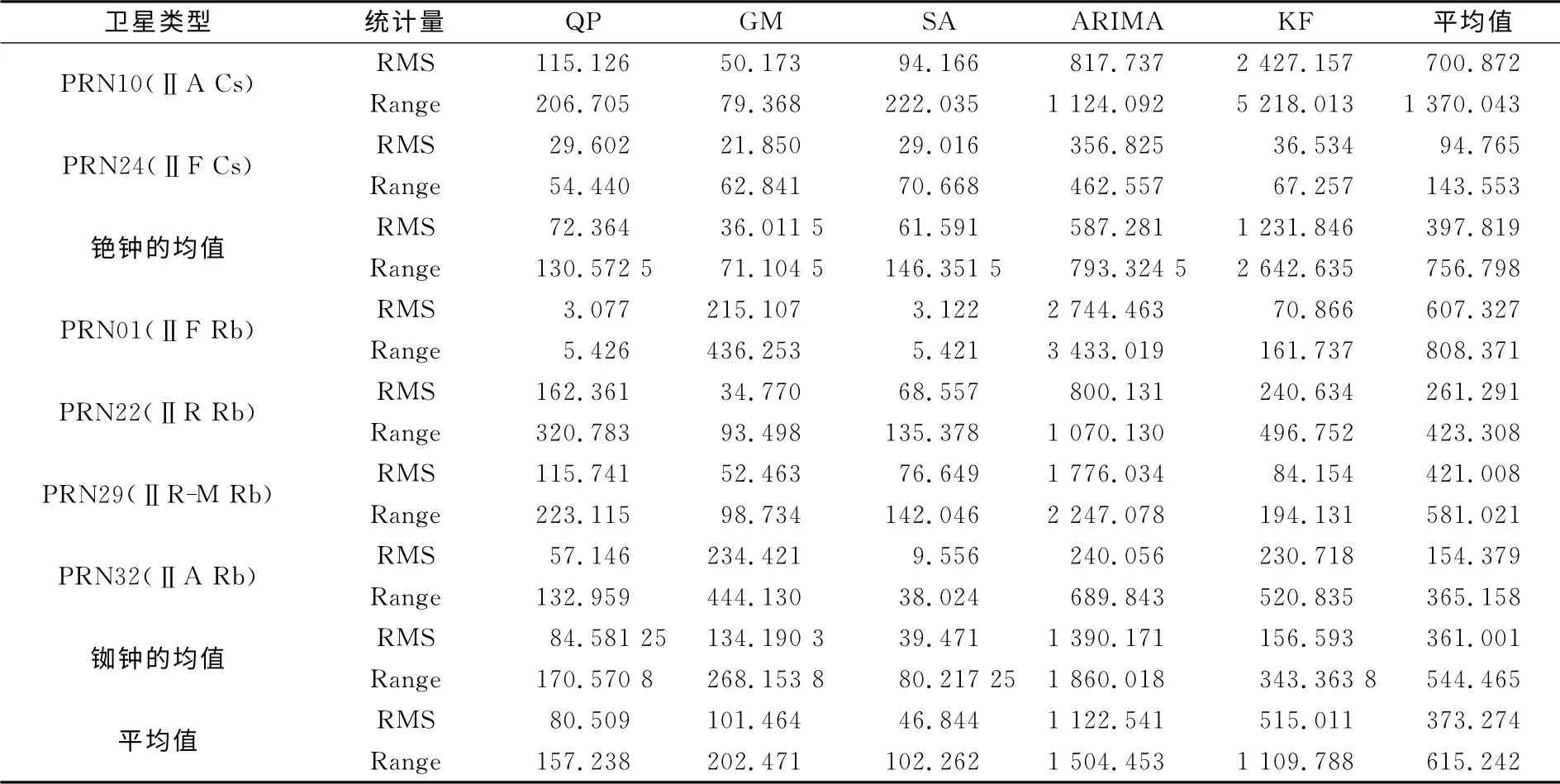
表5 方案二中5种模型15d预报结果的统计Tab.5 Statistics of prediction results for five models in 15day on the case two
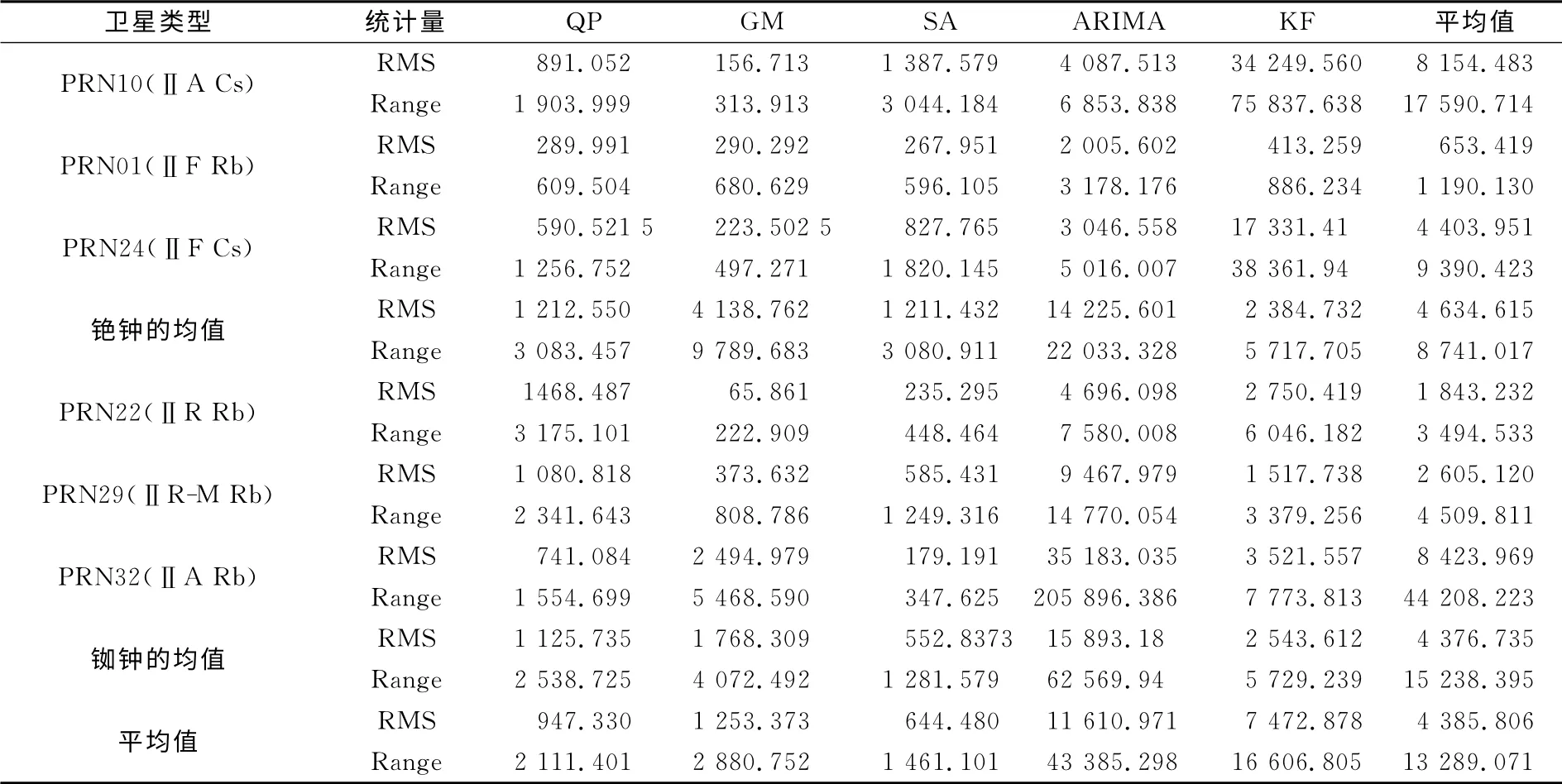
表6 方案二中5种模型60d预报结果的统计Tab.6 Statistics of prediction results for five models in 60day on the case two
4)分析6个表中ARIMA(p,d,q)模型对应列的统计数据可以看出:①该模型在钟差的短期预报中能够得到与前面3 种模型相当的预报结果;而在钟差的长期预报中,由于一次差分后的钟差数据并不是一个绝对平稳的时间序列,随着预报时间的增加,误差累积量急剧增加,所以这种方法并不适合钟差的长期预报。②由各表中6颗卫星的预报结果统计值可知,该模型进行钟差预报时,不同的卫星其钟差预报结果差异较大,这也说明了ARIMA(p,d,q)模型由于模型识别和阶数确定较为困难,预报结果的稳定性不好。
5)分析6个表中KF模型对应列的统计数据可以看出:①从表1、4可知,KF 模型利用1d的钟差数据建模进行短期预报时,预报结果的精度和稳定性与前4种模型相当。对比表1~3和表4~6可知,该模型进行长期预报时,一方面由于历史数据对滤波预报值的影响较大,初始数据的误差会被放大得越来越严重;另一方面滤波引入的系统状态方程虽然能有效顾及拟合精度,但其确定整体模型的精度较差,从而使得6颗卫星预报结果的精度和稳定性都随着预报时间的增加而变差。②由各表中6 颗卫星的预报结果统计可知,使用KF模型进行钟差预报时,其精度和稳定性随着星载原子钟的不同而变化。
6)分析6个表中铷钟钟差预报结果的平均值可看出,对于铷钟的短期预报,5种常用预报模型预报精度和稳定性基本相当,预报精度的平均值为ns量级。对比6个表中最后一列各颗卫星使用5种模型进行钟差预报时的统计结果平均值可知,相同预报条件下,不同种类的星载原子钟其钟差预报效果不同。同时,各模型预报效果随着原子钟类型的变化而不同。而对比各表最后一列中“铯钟的均值”与“铷钟的均值”可知,对于GPS系统卫星钟的预报,其星载铷原子钟的预报效果整体上优于铯原子钟。
7)对比表1、4,2、5和3、6可以看出,在钟差建模数据充足的条件下,由于SA 模型的周期函数根据较长的钟差序列得到了更可靠的确定,因此,其预报效果较QP模型有了改善;而该条件下这两种模型的预报效果优于GM(1,1)模型。根据6个表中的统计结果可知,5种模型在两种数据方案下,GM(1,1)模型的预报结果最为稳定,ARIMA 模型的预报结果随着建模钟差数据量及预报条件的不同而变化较大,QP、SA、ARIMA、KF 4种模型能够通过增加建模钟差数据量来改善模型的预报性能,特别是对于前3种模型的中长期预报。对于GM(1,1)模型,增加钟差建模数据使得短期预报结果的精度和稳定性均变差,也不能明显改善中长期预报效果。造成该现象的主要原因是对于GPS卫星钟差短期预报,该模型的指数系数是只与历元个数有关的函数,不同的建模钟差数据量会产生差异较大的预报结果。
2 结 语
1)QP模型具有建模简单、物理意义明确、短期预报效果好等优点,存在的不足是预报精度随着预报时间的增加而迅速变差。
2)SA 模型能够一定程度上顾及钟差的周期性变化部分,得到更为精确的钟差预报值;但该模型的周期函数要根据较长的钟差序列才能更可靠地确定,同时该模型的建立较QP模型更复杂。
3)GM(1,1)模型不但短期预报效果好且比较适合进行钟差的长期预报,存在的不足是模型的指数系数是与历元个数有关的函数,不同的建模钟差数据量会产生差异较大的预报结果;同时,还存在有时会出现较大预报误差的现象。
4)ARIMA 模型在钟差的短期预报中能取得较好的预报结果,但不适合钟差的长期预报;同时,该模型的预报效果会随着星载原子钟类型的不同和预报条件的变化而产生较大差异。
5)KF模型的优点是不仅能够预报钟差值还能实时求解出钟差、钟速和钟漂3个表征星钟特性的物理参数;但该模型的预报效果与先验信息认知程度等密切相关,通常难以较好地获取这些信息。该模型钟差短期预报效果较好,特别是在建模数据充足的条件下;但其钟差长期预报的效果较差,因此,不适合用来进行钟差的长期预报。
6)对于GPS系统,其星载铷钟的预报效果整体上优于星载铯钟。同时,在5种常用钟差预报模型中,QP模型和GM(1,1)模型较为简单,而且具有较好的预报效果。
[1]刘基余.GPS卫星导航定位原理与方法[M].北京:科学出版社,2008(Liu Jiyu.Theories and Methods of GPS Satellite Navigation and Positioning[M].Beijing:Science Press,2008)
[2]朱祥维,肖华,雍少为,等.卫星钟差预报的Kalman算法及其性能 分 析[J].宇航学报,2008,29(3):966-970(Zhu Xiangwei,Xiao Hua,Yong Shaowei,et al.The Kalman Algorithm Used for Satellite Clock Offset Prediction and Its Performance Analysis[J].Journal of Astronautics,2008,29(3):966-970)
[3]王宇谱,吕志平,陈正生,等.卫星钟差预报的小波神经网络算法研究[J].测绘学报,2013,42(3):20-28(Wang Yupu,LüZhiping,Chen Zhengsheng,et al.Research the Algorithm of Wavelet Neural Network to Predict Satellite Clock Bias[J].Acta Geodaetica et Cartographica Sinica,2013,42(3):323-330)
[4]王继刚.基于GPS精密单点定位的时间比对与钟差预报研究[D].北京:中国科学院研究生院,2010(Wang Jigang.Research onTtime Comparison Based on GPS Precise Point Positioning and Atomic Clock Prediction[D].Beijing:Graduate School of CAS,2007)
[5]崔先强,焦文海.灰色系统模型在卫星钟差预报中的应用[J].武汉大学学报:信息科学版,2005,30(5):447-450(Cui Xianqiang,Jiao Wenhai.Grey System Model for the Satellite Clock Error Predicting[J].Geomatics and Information Science of Wuhan University,2005,30(5):447-450)
[6]郑作亚,党亚民,卢秀山,等.附有周期项的预报模型及其在GPS卫星钟差预报中的应用研究[J].天文学报,2010,51(1):95-102(Zheng Zuoya,Dang Yamin,Lu Xiushan,et al.Prediction Model With Periodic Item and Its Application to the Prediction of GPS Satellite Clock Bias[J].Acta Astronomica Sincia,2010,51(1):95-102)
[7]Heo Y J,Cho J,Heo M B.Improving Prediction Accuracy of GPS Satellite Clocks with Periodic Variation Behavior[J].Measurement Science and Technology,2010,21(7):3 001-3 008
[8]Senior K L,Ray J R,Beard R L.Characterization of Periodic Variations in the GPS Satellite Clocks[J].GPS Solution,2008,12(3):211-225
[9]徐君毅,曾安敏.ARIMA(0,2,q)模型在卫星钟差预报中的应用[J].大地测量与地球动力学,2009,29(5):116-120(Xu Junyi,Zeng Anmin.Application of ARIMA(0,2,q)Model to Prediction of Satellite Clock Error[J].Journal of Geodesy and Geodynamics,2009,29(5):116-120)
[10]赵亮,兰孝奇,盛建岳.ARIMA 模型在卫星钟差预报中的应用[J].水利与建筑工程学报,2012,10(1):135-137(Zhao Liang,Lan Xiaoqi,Sheng Jianyue.Application of ARIMA Model in Satellite Clock Error Forecasting[J].Journal of Water Resources and Architectural Engineering,2012,10(1):135-137)
[11]Davis J,Bhattarai S,Ziebart M.Development of a Kalman Filter Based GPS Satellite Clock Time-Offset Prediction Algorithm[C].European Frequency and Time Forum(EFTF),2012
[12]郑作亚,陈永奇,卢秀山.灰色模型修正及其在实时GPS卫星钟差预报中的应用研究[J].天文学报,2008,49(3):306-320(Zheng Zuoya,Chen Yongqi,Lu Xiushan.An Improved Grey Model for the Prediction of Real-time GPS Satellite Clock Bias[J].Acta Astronomica Sinica,2008,49(3):306-320)
[13]Wang J G,Hu Y H,He Z M,et al.Prediction of Clock Errors of Atomic Clocks Based on Modified Linear Combination Model[J].Chinese Astronomy and Astrophysics,2011,35:318-326
[14]王宇谱,吕志平,陈正生,等.一种新的导航卫星钟差预报与内插方法[J].大地测量与地球动力学,2013,33(4):112-116(Wang Yupu,LüZhiping,Chen Zhengsheng,et al.A New Method of Navigation Satellite Clock Bias Prediction and Interpolation[J].Journal of Geodesy and Geodynamics,2013,33(4):112-116)

