全局最优化的一种新的拟全局下降法

刘呈军

(重庆水利电力职业技术学院，重庆 永川 402160)

关于凸优化问题已有许多文献对其做了研究，并有了一些很好的求解方法.然而，在自然世界中大多数的优化问题都是非凸的.当目标函数具有多个局部最小值时，这对求解全局最优解是一个很大的挑战.辅助函数法［1］是求解全局优化问题的一种常用方法，通过对目标函数做一些适当的修正来超越现有的局部最优解.

函数修正法(即隧道效应法)是由Levy 在1977年提出，并在1985年由Levy 和Montalvo 公开发表［2］.1989年，Yao 推广了这种隧道效应算法［3］求解约束全局最优化问题，后面又有作者对其进行的推广［4］.1983年葛仁溥提出了填充函数法［1］，并在1990年被发表.而后文献［5 -6］又将填充函数法进行了推广.

1 新的全局下降法

考虑无约束全局最优化问题:

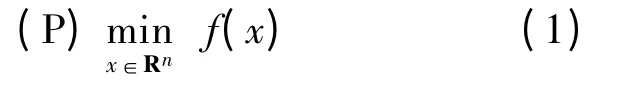
其中，函数f 在Rn上连续可微，并且对问题(P)作如下的假设.

假设1:存在一个点x00∈Rn，f0＞0 和一个箱子集i = 1，2，…，n}⊂Rn，使得x00∈Ω 和对∀x ∈Rnint Ω 有f(x)≥f(x00)+ f0．其中:int Ω 是Ω内部点的集合.

注意到如果f 满足强制条件，即当‖x‖ →+ ∞时f(x)→+ ∞，那么f(x)满足假设1．在假设1 的条件下问题(P)等价于下面的问题(PΩ)

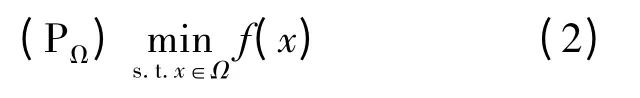
本文提出一种新的辅助函数法即拟全局下降法来适应函数修正法的第二阶段.它具有如下一些性质:

1)在任意给出的一个可能不是问题(P)的一个局部极小点x*处能够构造出全局下降函数;

2)满足f(x)≥f(x*)的任意点x (包含x*)不能是所构造的全局下降函数的一个平稳点.在Rn中用任何传统的局部搜索方法去极小化被构造的全局下降函数将会在全局下降函数的一个极小点或平稳点x＊＊(f(x＊＊)＜f(x*))处终止.

在后面讨论中，假设x*是满足f(x*)≤f(x00)的迭代算法中的当前点，其中x00满足假设1.

定义1 函数px*(x)称为问题(PΩ)在点x*的一个全局下降函数，如果px*(x)满足下面的条件:

1)函数px*(x)在Ω 上的任意平稳点都有f()＜f(x*)成立;

2)函数px*(x)在Ω 上的任意局部极小点，除Ω 的(至多)一个顶点外都有f()＜f(x*)成立;

3)如果L(x*)≠φ，即x*不是问题(P)的全局极小点，那么对任意的∈L(x*)是px*(x)在Ω 上的一个局部极小点和平稳点，而且有px*()＜px*(x*);对任意的x ∈∂Ω 有px*()＜px*(x)．

对一个给定的可变参数r ＞0 ，定义下面两个函数:

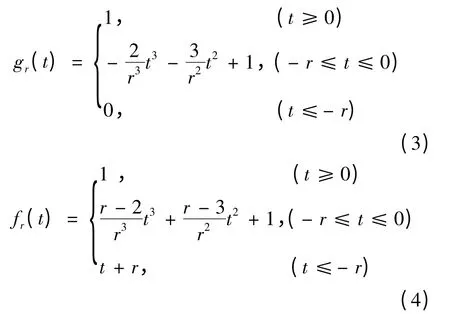
可以证明:gr(t)和fr(t)在R 上是可微的，且有

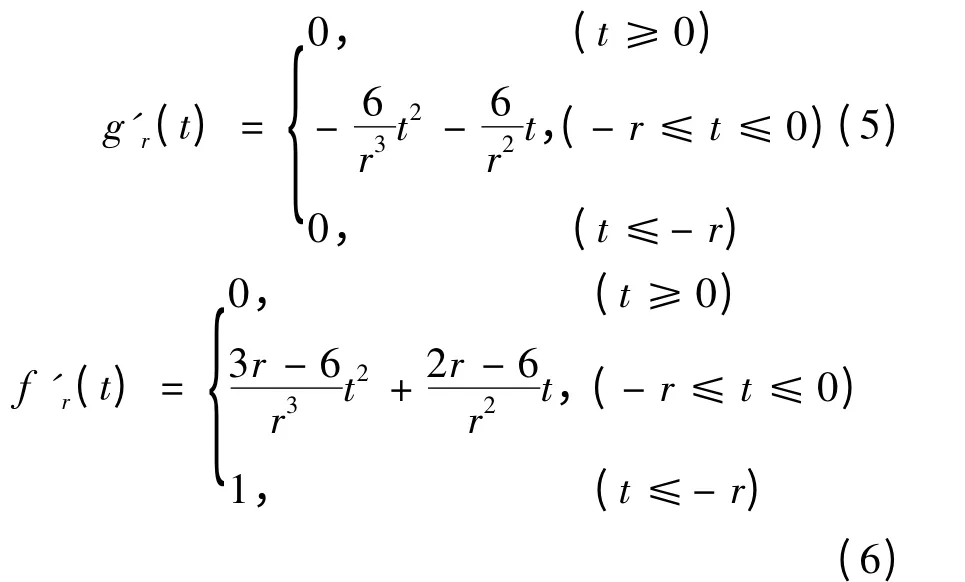
不失一般性，取点x0∈RnΩ 为

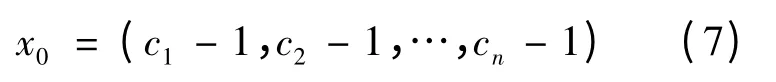
显然，对任意的x ∈Ω 有‖x -x0‖≥1 .取Ω 中离x0最远的顶点为

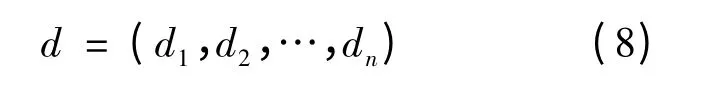
设

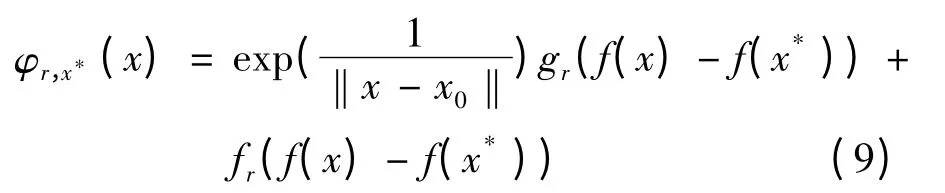
注意到，x*不是函数φr，x*(x)的平稳点.规定

可以证明，函数φr，x*(x)是一个全局下降函数，在函数修正法的第二阶段中采用上面所讨论的全局下降会导出一个求解算法.但在全局下降法第二阶段的数值计算时不太会令人满意，因为这个算法通常会在顶点d = (d1，d2，…，dn)处停止.为了实现满意的数值结果，对全局下降函数φr，x*(x)进行修正得到一个新的拟全局下降函数.

由假设1 可知，对任意的x ∈∂Ω 有f(x)≥f(x00)+ f0，若当前局部极小点或平稳点x*满足f(x*)≤f(x00)时，对任意的x ∈∂Ω 有f(x)≥f(x00)+ f0≥f(x*)+ f0.

设

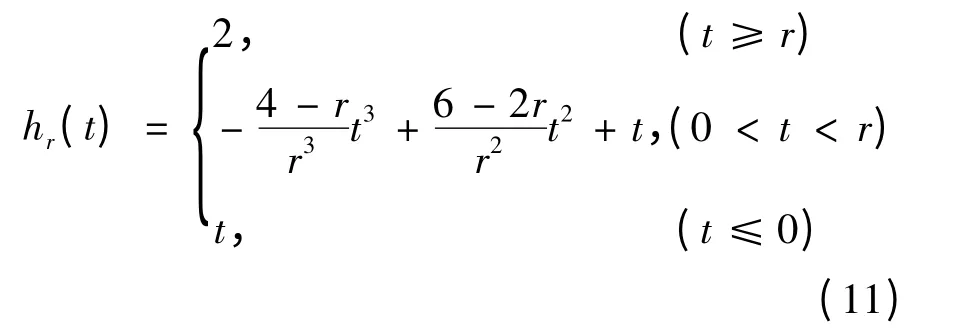
可以证明hr(t)在R 上是连续可微的，它的导数如下:

选择一个给定点x0∈RnΩ，使得对任意的x ∈Ω 有‖x - x0‖≥1．设

其中r 是大于0 的参数，而q 为加速下降率可以调整的参数.函数Qq，r，x*(x)具有下面的一些性质.

定理1 设假设1 成立，对∀r ＞0 有下面的结论成立:

①满足f(x)≥f(x*)+r 的任意x ∈Ω 不是Qq，r，x*(x)的平稳点.

②对满足▽f(x)= 0，0 ≤f(x)-f(x*)＜r 的 任 何 x 不 是 Qq，r，x*(x)的 平 稳 点，即▽Qq，r，x*(x)≠0．

有

对满足f(x)≥f(x*)的任意x 都有:

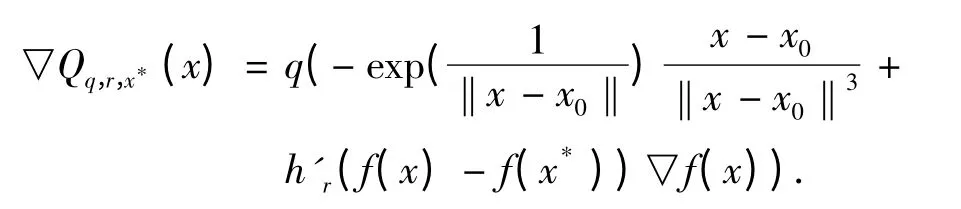
①满足f(x)≥f(x*)+ r 的任意x ∈Ω 有t= f(x)- f(x*)≥r，即有

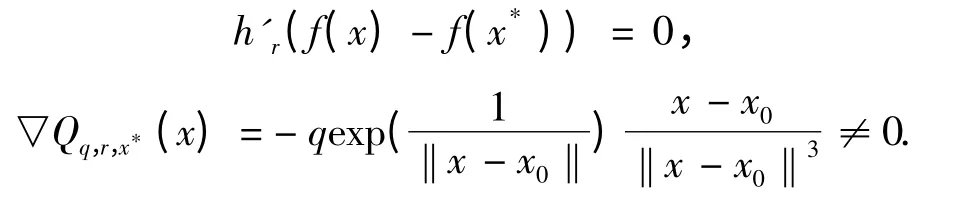
②对满足▽f(x)= 0，0 ≤f(x)-f(x*)＜r 的任何x 有

即▽Qq，r，x*(x)≠0．

定理2 假设

①假设1 成立，并且F 是一个有限集;

②L(x*)≠φ，即x*不是问题(P)的一个全局极小点.

证明 因为F 是一个有限集且L(x*)≠φ，所以是有限集且β0(x*)＞0．对任意的∈L(x*)，因为f(x*)- f()≥β0(x*)所以有f()- f(x*)≤- β0(x*)≤-2r ＜- r．由f(x)的 连 续 性 和L(x*)⊂int Ω，存在一个邻域N(，δ0)使得f(x)-f(x*)＜-r 以及f(x)≥f()．因此对任意的x ∈N(，δ0)时，

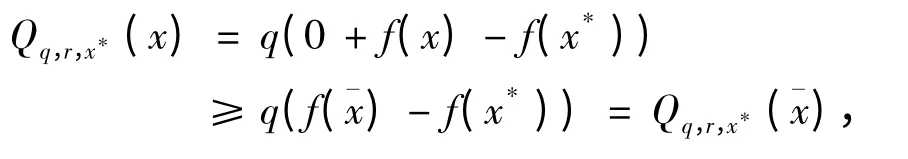
且

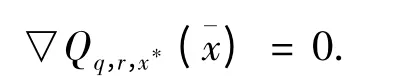
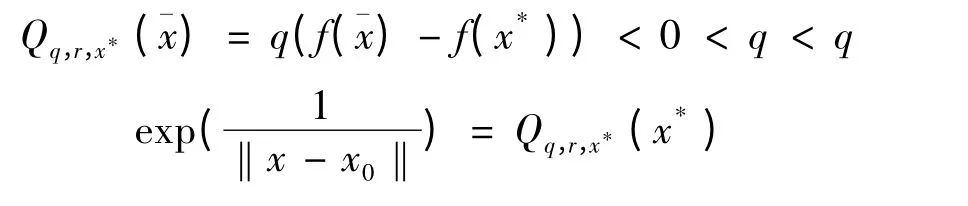
和对∀x ∈∂Ω 有

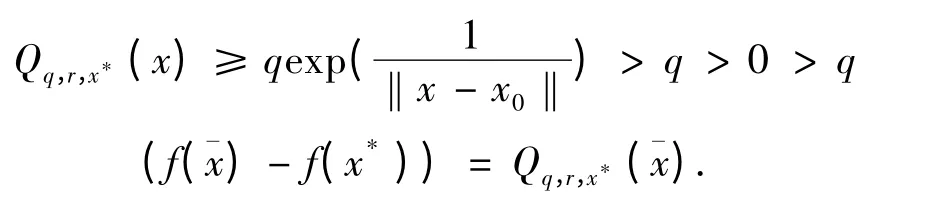
证明 对任意的x ∈∂Ω，r ≤f0有f(x)≥f(x*)+ f0≥f(x*)+ r．因此，

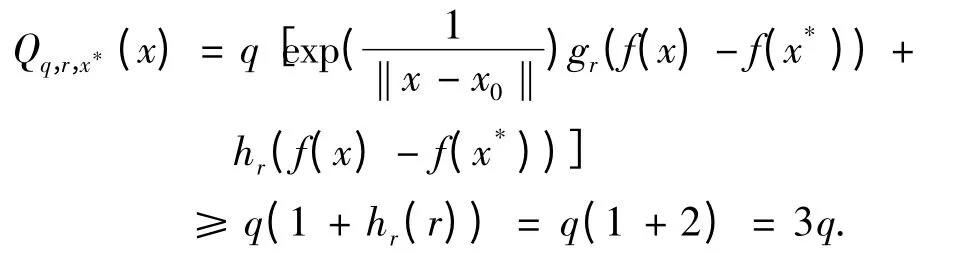
所以

因此，对任意的x ∈∂Ω 和0 ＜r ≤f0有Qq，r，x*(x*)＜Qq，r，x*(x).又因为Qq，r，x*()≤Qq，r，x*(x*)，∈Ω，所以∈int Ω．

满足▽f(x)≠0 和0 ≤f(x)-f(x*)＜r 的一 些 点 可 能 成 为 Qq，r，x*(x*) 的 平 稳 点，Qq，r，x*(x*)不是前面定义的全局下降函数，但是函数Qq，r，x*(x*)具有全局下降函数的几乎所有好的性质，因此称Qq，r，x*(x*)为拟全局下降函数.重要的是，采用拟全局下降函数防止了局部搜索过程跑到Ω 的边界上，拟全局下降函数在Ω上的任何局部极小点都是Ω 的内部点.

根据前面提出的拟全局下降函数Qq，r，x*(x*)，下面给出具体的求解算法，称这种算法为拟全局下降算法(QGDA).

QGDA 算法:

步0 选取一个较小的数μ ＞0 作为问题(P)极小化过程的参数r 的终止值，并且选取一个大的正数M ＞0 ，再选取一个点x0∈RnΩ 使得对任意的x ∈Ω 满足‖x - x0‖≥1 ，最后选取一个初始点x00∈Ω 使得x00满足假设1.

假设r0，q0分别是两个参数r，q 的初值，令k:= 0

步1 从x0k出发，使用局部极小化方法来获得问题(1)的一个局部极小点x*k．

步2 设

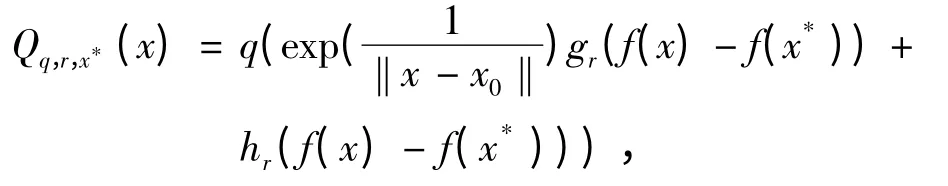
其中gr(t)，hr(t)分别由(3)式和(11)式给定.局部极小化方法求解问题(14):

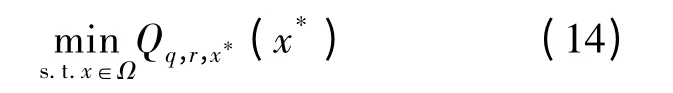
步3 若q ＜M，设q:= 10q 增加q 的值，然后转步2;否则，转步4.

步4 若r ＞μ，设q = q0，再通过设来减小r，然后转步2;否则停止.此时x*k即为极小化问题(P)的一个近似全局极小点.

注1 通常不需要验证假设1，因为很容易获得一个大的箱子集Ω．

2 数值计算

下面用本文中的拟全局下降算法来求解几个著名的检验函数.在下面的算例中，算法QGDA的步0 中，取

容易验证函数fG(x，y)是强制的，在本例中取并且取x0= (4，4)，x00= (1，1).利用本文中的拟全局下降函数法(QGDA)，在Matlab7.10 中最终求得Goldstein - Price 问题的最优解为x*=(0．0000，-1．0000)，最优值为f(x*)= 3．0000．

例2 Six - Hump Camel - back(n = 2)min fs(x)= 4x21-2．1x41+x61/3 -x1x2-4x22+4x42

解:在本例中我们取

并且取x0= (4，4)，x00= (0，0).取初始点x00=(1，1)和x0= (4，4)，通过本文中提出的拟全局下降函数法(QGDA)，利用Matlab7.10 求得Six-Hump Camel-back 问题的最优解为x*= (-0．089 8，- 0．712 7)，最优值为f(x*) =-1．031 6．

3 结论

针对全局最优化问题，本文介绍了一种新的拟全局下降法.这种算法只需用已有的局部搜索方法就可以求得原优化问题的全局最优解.本文中的拟全局下降算法利用了Matlab7.10 中的最优化工具箱里的最优化子程序.从本文中的几个算例结果来看，这种拟全局下降法是很有效的.

［1］Ge Renpu.A filled function method for finding a global minimizer of a function of several variables［J］.Mathematics Program，1990(46):191 -204.

［2］Levy A V，Montalvo A.The tunneling algorithm for the global minimization of functions［J］.SIAM Jouranal Sci.Stat.Comput.，1985，6(1):15 -29.

［3］Yao Y.Dynamic tunneling algorithm for global optimization［J］.IEEE Systems Man and Cybernetics Society，1989，19(5):1222 -1230.

［4］Chowdhury P R，Singh Y P，Chansarkar R A.Hybridization of gradient descent algorithms with dynamic tunneling methods for global optimization［J］.IEEE Systems Man and Cybernetics Society A，2000，30(3):384-390.

［5］Wu Z Y.A novel filled function method and quasi -filled function method for global optimization［J］.Computational Optimization and Applications，2006，34(2):249 -272.

［6］Zhang L S.A new filled function method for global optimization［J］.Global Optimization，2004(28):17-43.