利用PPP反演海潮负荷位移参数
郑 凯 马 兰 季 伟 郭博峰
1 武汉大学测绘学院,武汉市珞喻路129号,430079
海潮负荷效应会引起测站的位移[1-3]。目前,对海潮负荷引起的地表位移改正的主要方法是利用全球海潮模型计算,但由于利用卫星测高等资料建立的海潮模型在一些地区(特别是高纬度地区)模型改正精度不高,一些学者提出利用GPS技术测定海潮负荷位移参数的研究思路。Zhang等[4]用PPP技术获得了南极Amery冰架地区的海潮波形,采用5d连续观测的GPS数据反演得到8个分潮在垂直分量上的振幅和相位;Thomas等[5]比较了GPS 和VLBI技术测定海潮负荷位移参数的差异,表明利用GPS和VLBI技术测定海潮负荷位移参数是可行的,且PPP固定解计算得到的参数并没有较浮点解得到的参数在精度上有明显改善;Yuan等[6]利用香港12个测站3~7 a的GPS观测资料,采用与Thomas等类似的海潮负荷位移参数估算策略,将分潮参数与PPP模型其余参数一起估计。该方法虽然理论上比较严密,但增加了PPP 数据处理的复杂度,过度的参数化还可能造成分潮正余弦系数和模糊度参数及钟差参数之间的耦合相关性,也在一定程度上影响PPP定位的收敛速度。本文提出直接利用未顾及海潮负荷位移改正的动态PPP 解算得到的长时间(1a)测站坐标序列,采用傅里叶变换方法提取海潮周期信息,进而反演8个分潮的海潮负荷位移参数的方法,将反演结果与最新的5个全球海潮模型比较,分析评价该方法反演海潮负荷位移参数的可行性。
1 海潮参数反演方法
测站的海潮负荷位移可由11个主分潮的海潮负荷位移叠加获得,其中3 个为长周期分潮。由于反演长周期分潮需要长时间的观测数据,且长周期潮对测站位移的影响较其他分潮要小[7-8],故在此仅研究8 个主分潮,即4 个半日潮(M2、S2、N2、K2)和4个周日潮(K1、O1、P1、Q1)。
测站的海潮负荷位移可表示为:
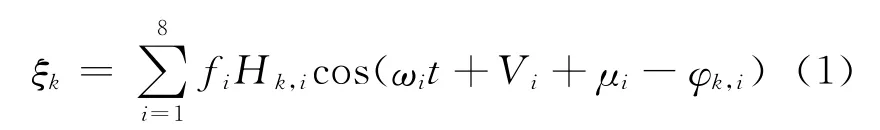
式中,Hk,i和φk,i分别为分潮i在k方向上的振幅和格林尼治相位;t为格林尼治时间;Vi为天文幅角初相(本文天文变量参考J2000.0系统);ωi为分潮角速度,可查表获得;fi和μi分别为节点因数和天文相角,可由天文变量计算得到;ξk为海潮负荷引起的测站位移偏差[9]。为便于求解Hk,i和φk,i,将式(1)改为:

式中,A=fiHk,icos(φk,i-μi),B=fiHk,isin(φk,i-μi)。由式(2)得:
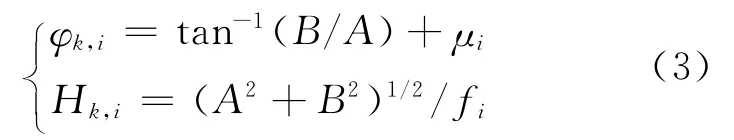
式中,A、B为待估参数,ξk为PPP计算得到的E、N、U3个方向的测站坐标序列。将式(2)以法方程形式表达,用经典最小二乘准则求解待估参数。考虑到φ变化范围从-PI到PI,实际解算结果需要加减180°。
2 PPP处理策略
海潮负荷对单点定位的影响在沿海地区可达mm级甚至cm级[1,4],因此在对其他误差精确改正之后,得到的测站位移即由海潮负荷引起。

本文采用无电离层组合的PPP模型[10-11]:其中,P为无电离层的伪距观测值,Φ为无电离层载波相位观测值,ρ为真实几何距离,dt为卫星钟差,dT为接收机钟差,Tr为对流层延迟,N为无电离层组合模糊度,λ为组合后的载波波长,ξ为系统误差(相对论效应、固体潮改正、地球自转改正、天线相位中心偏差及变化),ξoc为海潮负荷引起的位移偏差,εp和εΦ分别为伪距观测噪声和相位观测噪声。解算过程中,将测站坐标、接收机钟差、无电离层组合模糊度及对流层天顶延迟视为未知数,采用Kalman滤波作为参数估计器,卫星高度角设为7°,用TurboEidt方法探测周跳(不作修复)。同时,对接收机钟跳进行探测修复[12-13],采用绝对天线相位中心模型(IGS_08),用选权迭代的验后残差分析方法进行质量控制,并将模糊度当作实数处理。为了得到包含海潮信息的测站位移序列,不对海潮负荷引起的位移进行改正。卫星钟差、轨道以及硬件延迟选用IGS的精密产品。
由于相邻天之间解算数据的不连续以及精密产品不一致等原因,可能导致天与天的结果文件出现跳变。为解决此问题,将全年观测文件以7d为1组进行合并,如,1~7d,6~12d,…,共73个组合观测文件。对每个组合文件而言,因上述原因导致数据跳变的点只可能出现在文件的首尾时段。因此,对组合观测文件进行PPP动态解算之后,截取每组2~6d的解算坐标,然后融合成全年的测站坐标系列。
3 实例分析
3.1 数据
选取高纬度地区的3 个CORS 站AC67(57.798°N,152.336°W)、AC43(59.521°N,149.709°W)、AC39(58.610°N,152.394°W)以及中纬度地区的SHAO 测站(31.099°N,121,2°E)2012年全年的观测数据进行分析。由于缺乏测站坐标真值,故将各测站解算结果与首历元计算得到的测站坐标求差,并转换为E、N、U3个方向的坐标序列。实验表明,此方法会产生因地壳板块运动导致的坐标漂移。由于海潮负荷引起的位移仅是余弦波的叠加,故可通过一阶线性拟合的方式予以消除。考虑到数据量过大对计算机的性能要求也越高,将数据的采样率由30s稀疏为5min。
3.2 海潮负荷位移参数反演
为验证动态PPP 解算结果是否包含分潮信息,利用傅里叶变换对结果进行频谱分析。以测站AC43为例,将测站单天每个方向的坐标序列进行傅里叶变换后所得的振幅在频域内进行叠乘[14],可以分离出分潮信号与噪声。
图1给出了测站AC43的分潮周期图。可以很明显地看出周日潮和半日潮的周期信息,其次是1/3周日潮、1/4周日潮。可以看到,对测站而言,主要受周日潮和半日潮的影响,而1/3潮、1/4潮的影响仅为两主潮的1/6~1/7,就目前PPP精度而言可以不予考虑。图中长周期的分潮信息不明显,这是因为本文选用的数据时间跨度还不够长,不足以将更长周期的分潮信息提取出来。
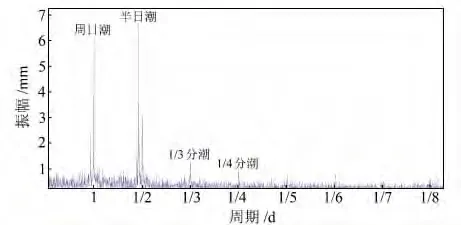
图1 测站AC43海潮频谱分析周期Fig.1 Ocean tidal periodogram spectrum analysis about station AC43
进一步从量化的角度分析。节点因数和天文相角近似线性变化如图2、3所示,相较于其他分潮,K2分潮的节点因数和天文相角的变动略为明显,分别为8%和1%左右。尽管如此,两者对海潮负荷位移参数的影响也在亚mm级[7],故在单历元参数处理中不予考虑,仅对最终结果取节点因数和天文相角的年均值进行改正。将测站位移代入式(2)、(3)式进行参数解算,解算结果与TPXO.7.2海潮模型计算结果进行比较,如表1、2所示。

图2 全年节点因数变化趋势Fig.2 Yearly change trend about nodal corrections which account for the modulating effect of the lunar node
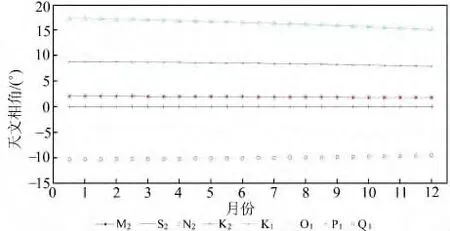
图3 全年天文相角变化趋势Fig.3 Yearly change trend about astronomical phase angle
3.3 结果评价
选用5个最新的全球海潮模型作为参考(表3),并采用均方根(RMS)[7]来评定PPP反演的参数和海潮模型计算值的差异。计算方法如下:
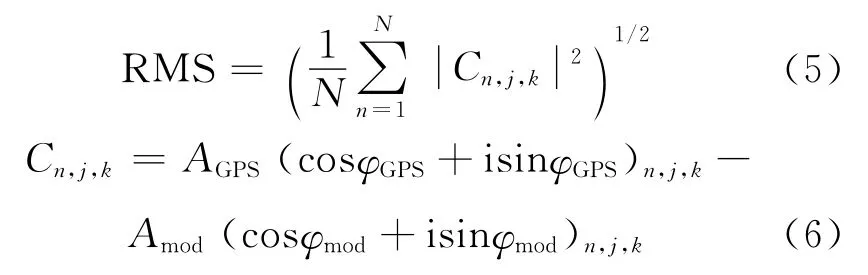
其中,A、φ分别代表振幅和相位,n(1,2,…,N)为测站号,j为分潮号,k为坐标分量,i为虚数符号。
图4给出了4个测站反演结果与TPXO.7.2模型计算结果的均方根。造成测站间差异的主要原因与测站所处的地理环境有关。例如,不同地区海潮负荷对地壳形变的影响程度不同,其中SHAO 测站在U方向上RMS 较小,尤其是K2分潮RMS约为其他3个站的1/3,是因为利用海潮模型计算的K2分潮在SHAO 测站的振幅仅为亚mm级,而其他几个测站K2分潮的振幅达到了几个mm,说明SHAO 测站受K2分潮的影响(尤其在垂直方向)较其他测站小很多。此外,在浅海地区由于复杂的地势,海潮模型并不能十分准确地反映分潮信息[15]。4 个测站在K1、K2分潮的均方根最为显著,主要是受轨道误差和多路径效应的影响[14]。
为进一步说明分潮的反演情况以及各模型间的差异,图5给出了PPP反演参数与5个海潮模型计算值之间的均方根误差统计结果。可以看到,除U方向Q1分潮各模型计算值有较大差异外,所选的5个全球海潮模型差异不大,说明在研究区域5个模型具有一致的精度。图中还发现,利用PPP反演出与太阳有关的分潮参数(S2、K2、K1、P1)与模型间的偏差较大,其中在水平方向上K2、K1略为明显,而在垂直方向上P1分潮的偏差则要高于K1。N方向的均方根误差整体优于2.5mm,E方向次之优于3.5mm,U方向相对偏差最大但仍优于6 mm,主要是垂直方向的定位精度低于水平精度所致。而影响均方根误差的原因除了和PPP 反演结果与模型间的系统偏差之外,数据长度也是一个重要原因。

表1 测站半日潮负荷位移参数反演结果与TPXO.7.2模型半日潮计算结果比较Tab.1 Compared PPP-derived results with TPXO.7.2about semi-diurnal constituents
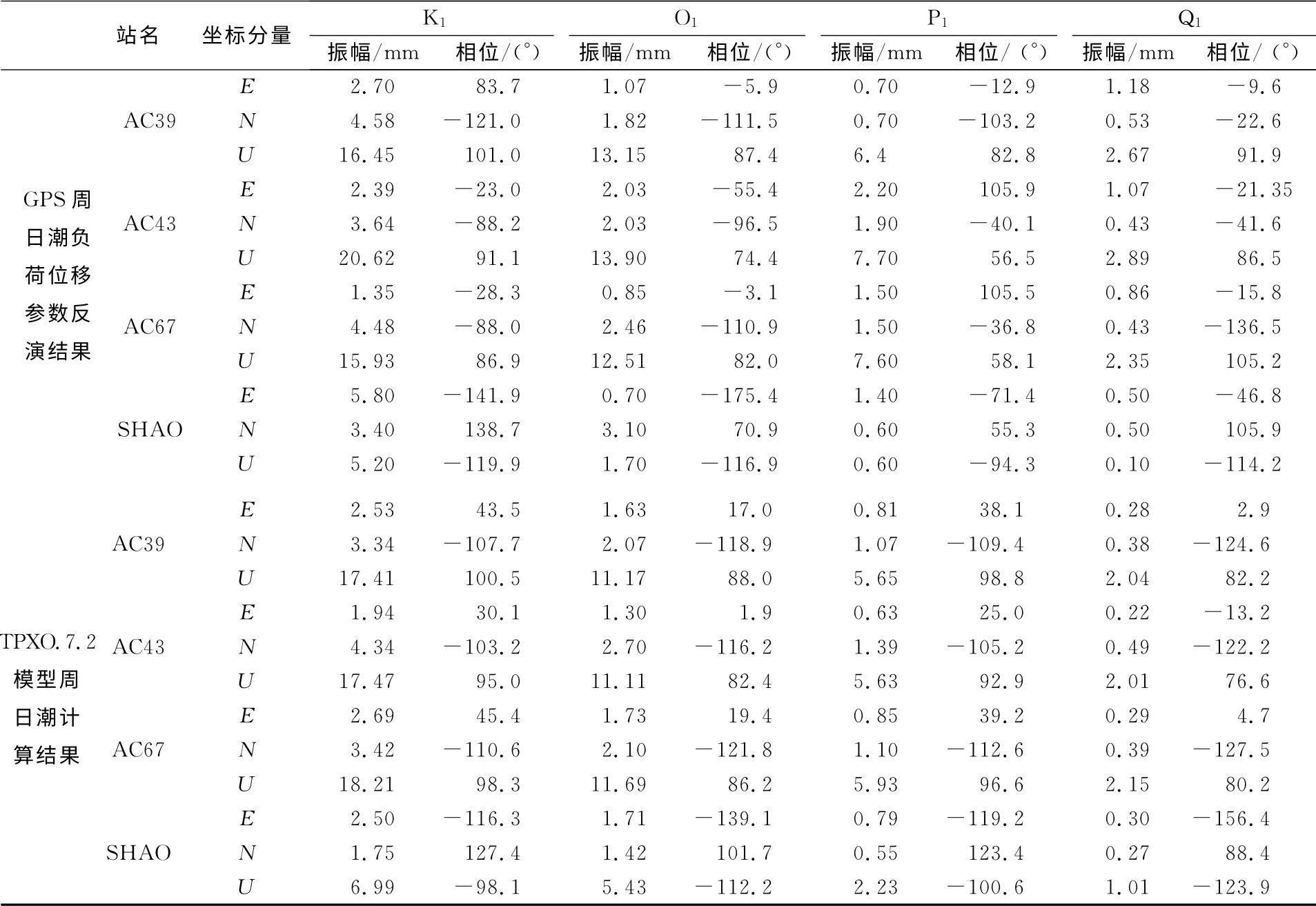
表2 测站周日潮负荷位移参数反演结果与TPXO.7.2模型周日潮计算结果比较Tab.2 Compared PPP-derived results with TPXO.7.2about ter-diurnal constituents

表3 全球海潮模型Tab.3 Global ocean tide model
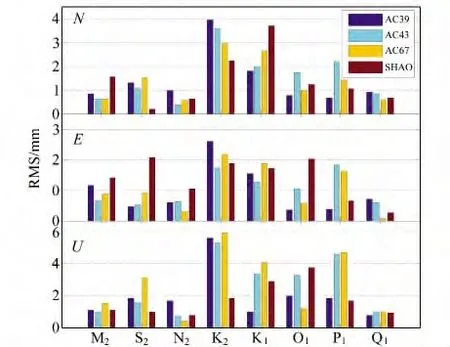
图4 PPP反演结果与TPXO.7.2模型之间的比较Fig.4 RMS of the PPP-derived OTL displacement estimates to the TPX.O.7.2model estimates
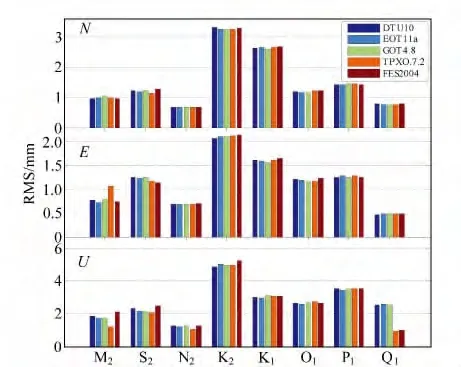
图5 PPP反演结果与模型的均方根误差Fig.5 RMS of the PPP-derived OTL displacement estimates to all ocean tide model estimates
在不考虑系统差的前提下,利用1a的GPS观测数据反演得到的参数与模型间的均方根误差与Yuan等[6]计算结果基本相当,这也说明利用本文方法反演海潮负荷位移参数可以较快地得到收敛。
4 结 语
1)本文方法计算的海潮负荷位移参数与模型间的均方根误差为mm级,与Yuan等[6]方法解算结果基本相当,说明利用本文方法计算海潮负荷位移参数是可行的。
2)除Q1分潮TPXO.7.2 和FES2004 与其他海潮模型有差异外,在中高纬地区本文所选5个海潮模型差异不明显。
[1]周江存,孙和平.海潮负荷对GPS 基线的影响[J].大地测量与地球动力学,2005,25(4):27-32(Zhou Jiangcun,Sun Heping.Effect of Ocean Tide Loading on GPS Baseline Measurement[J].Journal of Geodesy and Geodynamics,2005,25(4):27-32)
[2]郑祎,伍吉仓,王解先,等.GPS精密定位中的海潮位移改正[J].武 汉 大 学 学 报:信 息 科 学 版,2003,28(4):405-408(Zheng Yi,Wu Jicang,Wang Jiexian,et al.Ocean Tidal Displacement Corrections in GPS Precision Positioning[J].Geomatics and Information Science of Wuhan University,2003,28(4):405-408)
[3]Dragert H,James T S.Ocean Loading Corrections for Continuous GPS:A Case Study at the Canadian Coastal Site Holberg[J].Geophysical Research Letters,2005,27(14):2 045-2 048
[4]Zhang X H,Andersen O B.Surface Ice Flow Velocity and Tide Retrieval of the Amery Ice Shelf Using Precise Point Positioning[J].J Geod,2006,80:171-176
[5]Thomas I D,Peter M A K,Clarke J.A Comparison of GPS,VLBI and Model Estimates of Ocean Tide Loading Displacement[J].J Geod,2007,81(5):359-368
[6]Yuan L G,Ding X L,Zhong P.Estimates of Ocean Tide Loading Displacement and Its Impact on Position Time Series in Hong Kong Using a Dense Continuous GPS Network[J].J Geod,2009,83:999-1 015
[7]郗钦文.精密引潮位展开的精度评定[J].地球物理学报,1992,35(2):150-153(Xi Qinwen.The Evaluation on the Precision of the Development of the Tidal Generating Potential[J].Acta Geophysica Sinica,1992,35(2):150-153)
[8]周旭华,吴斌,李军.高精度大地测量中的海潮位移改正[J].测 绘 学 报,2001,30(4):327-330(Zhou Xuhua,Wu Bin,Li Jun.Ocean Tide Displacement Corrections in High Precision Geodesy[J].Acta Geodaetica et Cartographica Sinica,2001,30(4):327-330)
[9]黄祖珂,黄磊.潮汐原理与计算[M].青岛:中国海洋大学出版社,2005(Huang Zuke,Huang Lei.Tidal Theory and Calculation[M].Qindao:Publishing House of Ocean University of China,2005)
[10]Héroux P,Kouba J.Precise Point Positioning Using IGS Orbit and Clock Products[J].GPS Solution,2001,5(2):12-28
[11]Kouba J.A Guide to Using International GNSS Service(IGS)Products,Natural Resources Canada[EB/OL].http://igscb.jpl.nasa.gov/components/usage.html,2012
[12]Zhang X H,Guo B F,Guo F.Influence of Clock Jump on the Velocity and Acceleration Estimation with a Single GPS Receiver Based on Carrier-Phase-Derived Doppler[J].GPS Solutions,2013,17(4):549-559
[13]Ruymbeke M V,Zhu P,CadicheanuNat N.Very Weak Signals(VWS)Detected by Stacking Method According to Different Astronomical Periodicities(HiCum)[J].Hazards Earth Syst Sci,2007(7):651-656
[14]King M.Kinematic and Static GPS Techniques for Estimating Tidal Displacements with Application to Antarctica[J].J Geodyn,2006,41:77-86
[15]李大炜,李建成,金涛勇.利用验潮站资料评估全球海潮模型的精度[J].大地测量与地球动力学,2012,32(4):106-110(Li Dawei,Li Jiancheng,Jin Taoyong.Accuracy Estimation of Recent Global Ocean Tide Models Using Tide Gauge Data[J].Journal of Geodesy and Geodynamics,2012,32(4):106-110)

