价格跳跃行为视角下中国金融期货开盘效应的实证研究

王 新 超， 刘 晓 雪， 胡 俞 越

（北京工商大学 证券期货研究所，北京100048）

一、引 言

金融期货市场价格的开盘跳跃行为是隔夜持仓投资者和交易所监管者的关注焦点，对于隔夜持仓的投资者来说，交易日开盘的高开（低开）往往伴随着下探（弹升），尤其针对短线投资者而言，短期内的巨幅波动提高了交易的冲击成本，加剧了交易账户收益的不确定性风险；而对于市场运行的监管者而言，开盘时间的价格跳跃行为使得对交易者异常交易行为的管理难度增加，如大量或者多次申报并撤销会引导其他投资者的期货交易或交易开仓量较大，这些都会造成市场的不稳定性和恐慌行为，这也是期货交易所的监控重点，开盘效应（信息驱动模式下的跳跃行为符合“冲击－反应－融入”这一过程，且考虑到期现市场的交易时间差，故将开盘15分钟内的跳跃视为开盘效应）的高度不确定性是市场参与主体面临风险的直观体现。

资产价格日内跳跃行为的研究是市场微观结构理论的突破性进展，关于资产价格日内跳跃行为的识别方法主要分为两大体系：一是Nielsen和Shephard提出的基于高频数据检验资产价格过程是否存在跳跃行为的非参数方法（BN－S方法），双幂变差方法为日间行为识别到日内行为识别奠定了基础，其主要识别信息到达引起的有限次价格跳跃［1］；随之，Huang等基于双幂变差提出Z检验统计量，Lee和Mykland提出L－M检验方法、Andersen等提出序列跳跃检验方法进行逐时段跳跃检验，即采用BN－S方法确定存在跳跃的交易日并将日内价格改变最大的时段确定为跳跃时段，将检测出的跳跃时段剔除，对余下的数据重复以上方法直到不能检测出跳跃为止［2］［3］［4］，而Bollerslev等则基于Mancini已实现门限幂变差思想提出阈值的日内逐时段检测方法，且在阈值设定上加入了动态指标，提高了跳跃行为识别的准确性［5］［6］。二是Ait－Sahalia和Jocad提出的阈值多幂次变差方法（TMPV），其主要识别基于订单冲击的无限活跃跳跃行为［7］，且可以根据不同噪音的特点将噪音行为纳入分析体系；Corsi等则提出修正的已实现阈值多幂次变差（C－TMPV）检测高频持续性跳跃［8］。总之，资产价格日内跳跃行为的识别主要基于高频数据的非参数方法，BN－S体系方法相较TMPV体系方法更侧重有限次活跃跳跃的识别。

资产价格开盘效应的研究相对有限，具有代表性的如：Taylor、Andersen和刘庆富等的研究认为，隔夜收益所包含的信息是不容忽视的，考虑隔夜收益的模型可以更加精准预测日波动率，且隔夜收益是日收益的重要组成成分［9］［10］［11］；孙洁则通过建立HAR－CJN模型说明连续变差对预测的贡献最大，而跳跃变差的影响一般比连续变差的要弱［12］；简志宏等的HARCJ－M贡献在于将隔夜风险视为日内波动的延续，并将投资者心理因素引入刻画波动率的模型中提高样本外的预测能力［13］。

综上所述，关于资产价格日内跳跃行为的既有研究主要集中在识别方法的改进，关于资产交易日开盘效应的研究甚少，现存的研究主要集中在隔夜不确定性收益和日内波动的关系，而隔夜不确定性收益仅是开盘效应的部分行为。因此，本研究在识别日内价格跳跃行为的基础上，证明中国股指、国债期货开盘效应的存在，并改进HAR－CJ波动率模型以分析信息驱动下股指期货开盘效应的内在机制，以期为市场投资者和监管者提供风险管理的实证依据。

二、实证模型和数据选择

1.数据说明

本研究的数据为2010年4月16日至2014年7月31日期、现货市场5分钟高频交易数据，数据来源于中国金融期货交易所，其中，主力合约数据是按照期货的成交量最大的合约整理而成。涉及数据的具体情况：（1）沪深300股指期货5分钟高频数据（2010年4月16日至2014年7月31日），数据样本量为56 214个，共1041个交易日，每个交易日共56个样本点，54个样本区间；（2）沪深300指数现货5分钟高频数据（2010年4月16日至2014年7月31日），数据样本量为49 968个，共1041个交易日，每个交易日共50个样本点，48个样本区间；（3）中国国债期货为2013年9月6日至2014年7月31日，样本为11 772个交易数据，共218个交易日，每个交易日分为56个样本点，54个样本区间。

2.资产价格日内跳跃识别方法：JV－TOD

本文研究选择的实证模型为Bollerslev等提出的JV－TOD非参数方法［5］，主要原因有：（1）研究对象是信息驱动下的金融期货日内开盘效应及其内在机制，相较于TMPV系方法，BN－S系识别方法在有限次跳跃方面准确度更高，订单驱动模式下的无限跳跃行为产生巨大风险的概率较低；（2）JV－TOD非参数方法阈值设定上考虑到日内扩散变差（连续性波动）的动态特征，提高日内价格跳跃行为识别的准确性；（3）JVTOD非参数分离方法不仅能够确定发生跳跃行为的交易日，且能够识别日内发生跳跃行为的分布时间点和具体幅度大小。

其中，RVt表示交易日波动的已实现变差，BVt表示交易日连续性波动的双幂变差，T和n＋1分别表示样本交易日天数和每个交易日等距离观测值，t＝1，…，T，则整个样本区间的离散点分别为，其中任意一个离散间隔区间为，其所对应的高频时间区间价格收益率为τ＝1，2，3，…，nT；Bollerslev等考虑了日内大致呈现U形特征不同时段扩散变差与日平均变差的动态比率，则有：

其中，i＝1，2，…，n，γ大于0，ῶ∈（0，0.5）且都是常数，参照既有文献并考虑中国期货市场实际情况取值：γ＝2＝0.49，意思是当日内高频区间收益率只要高于局部时间点连续波动集合2倍时就确认发生价格跳跃行为；阈值标准为，确认发生价格跳跃行为的时间点为，跳跃时间点的跳跃绝对值大小为JVt，则有：

3.研究开盘跳跃机制的改进HAR－CJ模型

期货隔夜不确定收益视为开盘效应的部分行为，假设：（1）期货市场的开盘跳跃行为是前期交易日日内价格波动行为的延续；（2）期货投资者对未来变化（信息）的预期会提前反映到市场波动特征上；（3）信息（包括隔夜、日内信息发布）驱动是引发交易日内时间段跳跃行为的主要因素。根据股指期货日内价格行为分布特征改进HAR－CJ模型进行实证。如公式（7）所示，Jkp，t＋1表示股指期货开盘15分钟内发生的跳跃绝对数值大小，CVd，t、CV3d，t、CV5d，t分 别表示 当日、前3日和前5日的连续性波动均值（交易日开盘必须发生价格跳跃行为），JVd，t、JV3d，t和JV5d，t分别表示当日、前3日和前5日的跳跃波动均值；JRmax，t表示交易日内价格跳跃的最大值；FRVt表示股指期货收盘前15分钟的已实现波动率，FJVt表示当日收盘前15分钟的跳跃波动；μt表示预测的误差。

三、实证结果与分析

1.JV－TOD模型结果与分析

股指期货交易日的已实现波动值和双幂变差值的分布情况如图1所示。

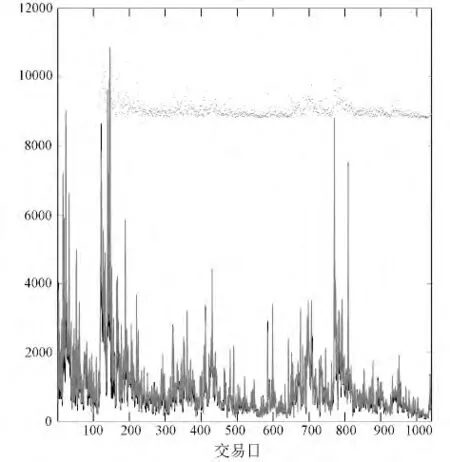
图1 股指期货1041个交易日的RVt、BVt值分布

从图1可以看出，第一，已实现波动值大于双幂变差值的交易日发生概率较大，即品种推行以来股指期货日内跳跃行为已成为常态；第二，交易日跳跃行为呈现两个较为集中的时段：2010年11月至2011年2月；2013年6月至2013年8月。主要原因可能有：一是投资者对宏观经济不稳定情况产生差异性预期；二是年中和年末货币市场流动性趋紧，市场价格出现巨幅震荡整理的情况。

TODi表示交易日内不同时间点的扩散变差与日平均变差的比率变动情况（见图2），其衡量股指期货交易日内连续性波动的特征形态，此动态指标对分离连续性波动和非连续性波动有重要理论意义，中国股指期货TODi值在日内大致呈现“3∧”形态，第一个峰值约在9：45，第二个峰值约在11：10，第三个峰值约在14：15，TODi日内均值约为0.7、最大值约为1.2、最小值约为0.35，但这一结论与Bollerslev等的分析有所差异，其认为TODi在日内呈现“U”形态［5］。股指期货日内价格跳跃行为的识别方面代表交易日内任意时间段的价格变动情况表示考虑扩散变差与日均变差比值的阈值条件。研究发现：交易数据中56214个样本点有5659个样本点发生跳跃行为，占比约10.01%，平均到每个交易日内约发生5～6次跳跃行为。

在股指期货日内价格跳跃的频数分布方面（见图3），股指期货日内跳跃较为集中的时间点有：9：20、9：45、11：25、13：35、14：05、14：35、15：15，跳跃频数集中分布的区间有：9：35～9：45、11：00～11：30和14：20～14：45，这说明：（1）股指期货日内价格的开盘跳跃、盘中跳跃、午盘跳跃和收盘跳跃行为皆十分明显；（2）隔夜信息的融入和宏观经济数据的发布可能是引发跳跃行为的重要因素，9：30和13：30是国家重要的月度宏观经济数据发布的日程时间点，9：35跳跃可能亦归因于股票市场的开盘溢出效应。国债期货对宏观经济信息的反应程度相对较高［14］，故比较分析5年期国债期货日内跳跃行为分布与之差异（见图4），交易日内9：40和10：45是跳跃频数最高的时间点，9：20是交易日内跳跃频数的次高点，14：50是跳跃次数的第三高点；从日内跳跃行为高频数分布区域来看，9：20～9：40、10：30～10：45、14：50～15：15为三段比较集中的区域，且第一时间段的跳跃行为分布最为密集、持续时间更长，第二时间段（盘中）的跳跃行为在分布密集度上高于第三时间段（收盘）的频数，说明国债期货日内价格跳跃的开盘跳跃大于盘中跳跃，并大于收盘跳跃，其午盘跳跃不显著。总之，午盘价格跳跃行为和盘中价格跳跃行为是股指期货显著区别于国债期货日内的分布特征，开盘跳跃行为是股指期货和国债期货日内价格行为的重要组成部分，且皆是各自日内频数分布的次高点。

除此之外，基于JV－TOD方法识别股指期货开盘15分钟内发生价格跳跃行为的交易日，结果显示，共有245个交易日存在开盘跳跃风险，约占总体的24%，有23个交易日开盘15分钟内至少发生2次价格跳跃，222个交易日开盘15分钟内发生1次跳跃，占比约为91%，且大部分发生在9：20。说明股指期货开盘价格存在较高不确定性风险，开盘效应较为明显，隔夜不确定性收益不能准确刻画期货市场开盘价格行为特征。

图2 股指期货TODi日内动态变化情况

图3 股指期货日内跳跃频数分布情况

图4 中国国债期货日内跳跃频数分布情况

2.股指期货开盘效应对其日内波动及现货开盘行为的影响

股指期货开盘效应对其日内波动的影响方面（见表1），参数γ表示高频数据中的任意区间收益率超过随机波动率局部估计值的倍数，γ＝2时，股指期货共有245个交易日发生开盘跳跃行为；γ＝1.5时，发生开盘跳跃行为的交易日有441个；γ＝3时，股指期货的开盘跳跃交易日共有66个，表明定义跳跃行为的波动值越大，发生跳跃行为的次数则越低。分别识别开盘效应交易日的连续性波动值和跳跃波动值，结果说明：日内开盘发生跳跃行为的频数对日内波动影响显著，即随着开盘跳跃行为数量的增加，其对日内连续、非连续波动行为影响增大，开盘效应是日内价格行为的重要组成部分。

表1 期货开盘跳跃差异化对日内波动的影响

股指期货开盘效应对指数现货市场的影响如图5和图6所示。

图5 γ＝2时期现开盘共同跳跃差值

图6 γ＝3时期现开盘共同跳跃差值

当γ＝2时，分别对期现市场的开盘跳跃行为进行识别，在1041个样本交易日，期现开盘发生共同跳跃的交易日有151天，占总体约15%。说明在同样的识别条件下，期货与现货市场的开盘价格行为发生一定概率的共震现象，可能期货引导现货或两者由共同的因素驱动；分析共同跳跃交易日的期、现开盘跳跃差值动态的特征，大部分交易日两者跳跃幅度接近，说明期货市场对现货市场行为的引导作用明显，沪深300指数市场的开盘跳跃行为可以由期货市场开盘效应来解释。当γ＝3时，现货市场发生开盘跳跃行为的交易日有113天，期货市场发生开盘跳跃行为的交易日有66天，但期现开盘发生共同跳跃的交易日仅有12天，说明期货市场开盘跳跃的极端行为对现货开盘行为的引导作用较弱，即一是期货、现货市场的开盘“非常规”波动行为可能更多是重大风险事件冲击而成；二是相较于“常规性”波动行为，“非常规”波动在股指期货市场上融入速度较快，对滞后交易时刻和其他市场的溢出效应较小，即开盘的极端跳跃行为大概率由“非理性”较快转为“理性”。

3.改进HAR－CJ模型回归结果分析

考虑股指期货价格行为的日内特征改进HAR－CJ类模型（公式7）进行实证，结果如下：模型的拟合优度为0.3，模型总体的F检验值通过，说明前期解释变量总体能够在一定程度上拟合开盘跳跃数值的变动。具体来看，显著的解释变量有CVd，t、CV5d，t和JV5d，t，即t期当日、5日均值的连续性波动、5日均值的跳跃性波动解释力度较好，说明日内波动行为包括连续部分和非连续部分都可以在有一定程度上解释期货价格的开盘跳跃效应，该结论与孙洁的研究一致［12］；t期交易日内最后15分钟的波动（连续、非连续）行为对下一交易日的开盘效应解释力度较差，这与经验上市场价格波动惯性理论相悖，说明此时间段的连续性波动和跳跃性波动是价格的瞬时行为，其影响能够较快地被市场所融入，惯性跳跃行为在t＋1交易日开盘期间出现的概率较低。简志宏、李彩云通过OLS回归和分位数回归分析沪深300指数收市前5分钟的已实现波动对隔夜收益的影响，发现除价格极端情况下影响都较为显著［13］。导致结论差异的可能原因有：（1）研究对象的差异性，开盘跳跃行为包括了隔夜收益的不确定性和其后续价格波动性；（2）回归变量选择的问题，简志宏等的研究试图将隔夜不确定性收益视为日波动率的重要调整项［13］，但夜间价格不像在交易时间内那样连续变动，因而隔夜波动率的特征和已实现波动率差别较大，所以将其视为已实现波动率的一部分来建模并不合适，应适宜单独建模，否则容易产生估计误差。

表2 改进HAR－CJ模型的实证结果

四、结论与建议

本文基于JV－TOD非参数方法和高频数据识别中国股指、国债期货市场日内价格跳跃行为，证明开盘效应的存在并根据市场预期理论改进HAR－CJ波动率模型分析开盘效应的内在机制，主要实证结论有：

（1）中国金融期货市场日内开盘效应明显，开盘跳跃行为是期货日内波动的重要组成部分。基于JVTOD方法识别出股指期货开盘15分钟内发生价格跳跃行为的交易日，结果显示有245个交易日存在开盘跳跃风险，约占总体24%。有23个交易日开盘15分钟内至少发生2次价格跳跃，222个交易日开盘15分钟内发生1次跳跃，占比约91%，且90%概率发生在9：20，证明开盘效应明显。且随着开盘跳跃行为数量的增加，其对日内连续、非连续波动行为影响愈为显著，开盘效应是日内价格行为的重要组成部分。

（2）股指期货日内价格的开盘跳跃、盘中跳跃、午盘跳跃和收盘跳跃行为皆十分明显，午盘价格跳跃行为和盘中价格跳跃行为是股指期货显著区别于国债期货分布的日内特征。股指期货日内跳跃较为集中的时间 点 有：9：20、9：45、11：25、13：35、14：05、14：35、15：15，跳跃频数集中分布的区间有：9：35～9：45、11：00～11：30和14：20～14：45；而国债期货日内跳跃高频数分布区域为：9：20～9：40、10：30～10：45、14：50～15：15，隔夜信息涌入下的开盘跳跃行为是金融期货（股指、国债）面临的主要风险。

（3）期现市场开盘共同发生“常规性”跳跃时，期货市场开盘效应对现货市场行为的引导作用明显，股票指数现货市场的开盘跳跃行为可以由期货市场行为来解释，但期货市场开盘跳跃的极端行为对现货开盘行为的引导作用较弱；分别对期、现市场的开盘“常规性”跳跃进行识别，在1041个样本交易日，期、现开盘发生共同跳跃的交易日有151天，且共同跳跃交易日的两者开盘跳跃差值大概率在零附近波动，说明期货市场对现货市场行为的引导作用明显。

（4）日内波动行为包括连续部分和非连续部分都可以在一定程度上解释期货价格的开盘跳跃效应，但相较而言，跳跃变差比连续波动的预测贡献稍弱。HAR－CJ模型的实证结果表明：显著的解释变量有CVd，t、CV5d，t和JV5d，t，即t期当日、5日均值的连续性波动、5日均值的跳跃性波动解释力度较好，说明日内波动行为包括连续部分和非连续部分都可以在一定程度上解释期货价格的开盘跳跃效应。

根据上述实证结论，本文为机构投资者和期货市场监管者提供相关建议如下：

（1）根据期现市场“常规性”共同跳跃绝对值差的规律性特征，股指期货投资者可以设计程序化统计套利的策略，如期货开盘跳跃值与现货开盘跳跃值绝对差大于零，则应卖出期货，买入现货，但统计套利策略的应用须遵循适用的市场条件，并结合逻辑主导下基本面分析，完善风险控制、管理机制。

（2）根据股指期货日内价格跳跃的分布特征，市场监管者在跳跃频数集中分布区间即9：35～9：45、11：00～11：30和14：20～14：45加强对市场波动的监控；监管者可监控跟踪月度数据公布前5个交易日市场的连续性、非连续波动变化情况，估计市场参与者的情绪对当期开盘波动的影响，做到有效监控、及时管理，进而规避较大的不确定风险，防止市场过度反应；同时，机构投资者可以在预测模型的方程中引入5日均值连续性、非连续性指标，提高对期货、现货市场波动率拟合的准确度。

（3）股指期货市场上开盘极端跳跃行为对现货市场波动溢出效应较弱，则现货市场上的投资者应避免过度参考期货市场开盘极端行为产生“恐慌式”交易；期货开盘的极端跳跃行为不应该成为监管者对现货市场开盘进行重点监控的理由。

（4）国债、股指期货市场监管者应积极推行夜盘交易，以充分吸收隔夜信息，降低其对市场波动的影响。样本期间内，9：20是日内跳跃频数的次高点，是金融期货开盘效应的重要特征之一。若国债和股指期货市场推行夜盘交易，国外重要经济信息在市场能够得到有效稀释，减少次日开盘的跳跃行为，降低交易日内波动率［14］；此外，金融期货夜盘交易的推出也将吸引更多国外机构投资者积极参与到国内市场来，对于完善中国金融期货市场结构和提高期货市场的价格发现能力具有重要意义。

［1］BARNDORFF－NIELSEN O E，SHEPHARD N.Power and bipower variation with stochastic volatility and jumps［J］.Journal of financial econometrics，2004，（1）：1－37.

［2］HUANG X，TAUCHEN G.The relative contribution of jumps to total price variance［J］.Journal of financial econometrics，2005，（4）：456－499.

［3］LEE S S，MYKLAND P A.Jumps in financial markets：a new nonparametric test and jump dynamics［J］.Review of Financial studies，2008，21（6）：2535－2563.

［4］ANDERSEN T G，BOLLERSLEV T，FREDERIKSEN P.Continuous－time models，realized volatilities，and testable distributional implications for daily stock returns［J］.Journal of Applied Econometrics，2010，25（2）：233－261.

［5］BOLLERSLEV T V，TODOROV S Z.Jump tails，extreme dependencies，and the distribution of stock returns［J］.Journalof Econometrics，2013，172（2）：307－324.

［6］MANCINI C.Non－parametric threshold estimation for models with stochastic diffusion coefficient and jumps［J］.Scandinavian Journal of Statistics，2009，36（2）：270－296.

［7］AIT－SAHALIA Y，JACOD J.Testing for jumps in a discretely observed process［J］.The Annals of Statistics，2009，37（1）：184－222.

［8］CORSI F，PIRINO D，RENO R.Threshold bipower variation and the impact of jumps on volatility forecasting［J］.Journal of Econometrics，2010，159（2）：276－288.

［9］NICHOLAS T.A note on the importance of overnight information in risk management models［J］.Journal of Banking ＆Finance，2007，31（1）：161－180.

［10］ANDERSEN T G，BOLLERSLEV T，HUANG X.A reduced form framework for modeling volatility of speculative prices based on realized variation measures［J］.Journal of Econometrics，2011，160（1）：176－189.

［11］刘庆富，朱垚，方力.股指期现货间的跳跃扩散效应及其信息含量——基于跳跃变量回归模型的新证据［J］.复旦学报（社会科学版），2013，（4）：17－25.

［12］孙洁.考虑跳跃和隔夜波动的中国股票市场波动率建模与预测［J］.中国管理科学，2014，（6）：114－124.

［13］简志宏，李彩云.隔夜风险可以预测吗——基于HARCJ－M模型的高频数据分析［J］.管理评论，2014，（2）：3－11.

［14］杨婉茜，成力为.金融危机前后国债收益率曲线变动的潜在因素分析［J］.大连理工大学学报（社会科学版），2014，35（1）：86－91.