Rota-Baxter Operators of Weight 1 on 2×2-matrix Algebras

LI JIN-ZHI AND LIU WEN-DE

(School of Mathematical Sciences,Harbin Normal University,Harbin,150025)

Communicated by Du Xian-kun

Rota-Baxter Operators of Weight 1 on 2×2-matrix Algebras

LI JIN-ZHI AND LIU WEN-DE*

(School of Mathematical Sciences,Harbin Normal University,Harbin,150025)

Communicated by Du Xian-kun

In this paper we determine all Rota-Baxter operators of weight 1 on 2×2-matrix algebras over an algebraically closed feld.

Rota-Baxter operator,weight,associative algebra

1 Introduction

Rota-Baxter algebras or their corresponding Rota-Baxter relations came from[1],which are on integral equations of fuctuation theory.After that,many mathematicians paid attention to this concept,and especially,Rota[2]fundamental papers around 1970 brought the subject into the areas of combinatorics and algebras.In fact,Rota-Baxter relation may be regarded as one possible generalization of the standard shufe relation in[2-3].In the case of Lie algebra,when the weightλ=0,the Rota-Baxter relation is just the form of classical Yang-Baxter equation(CYBE)and when the weightλ=1,it corresponds to the operator form of the modifed classical Yang-Baxter equations.The broad connections of Rota-Baxter algebras with many areas in mathematics and mathematical physics are remarkable.However,the theoretical study of Rota-Baxter algebras is still in its early stage of development.In recent years,some articles have been published about Rota-Baxter algebras in[3-8].Especially,An and Bai[7]have not only worked over Rota-Baxter operators of weight 0 on pre-Lie algebras,but also computed all Rota-Baxter operators of weight 0 on associative algebras of dimensions≤3;Li and Hou[8]have given all Rota-Baxter operators of weight 1 on associative algebras of dimensions≤3.

In this paper,we study the Rota-Baxter operators of weight 1 on the associative algebraM2(F)consisting of 2×2-matrix over an algebraically closed feld F.The paper is organized as follows.In Section 2,we give all Rota-Baxter operators of weight 1 onM2(F).In Section 3,we analyze how to prove the previous theorem and establish the corresponding equations. In Section 4,we give the proof of the main theorem.Throughout this paper,all algebras are of fnite dimensions and over an algebraically closed feld F.

2 Main Results

We adopt the following defnition from[3].

Defnition 2.1A Rota-Baxter algebra is an associative algebra A overFwith a linear operator R:A→A satisfying the Rota-Baxter relation:

where λ∈Fis a fxed element,which is called the weight of R.

Theorem 2.1All the Rota-Baxter operators of weight1on2×2-matrix algebra M2(F)are Riand I-Ri∈RB(M2(F)),i=1,2,···,31,shown in Table2.1,where a,b,c∈F(any denominator is nonzero and non-appeared parameters in matrices are zero).

Table 2.1 The Rota-Baxter operators set

(continued)

3 Analysis

Lemma 3.1[8]Let R be a linear operator on the algebra A.Then R∈RB(A)if and only if I-R∈RB(A)(I is the identity mapping of A).In particular,0,I∈RB(A).

LetAbe an associative algebra with a basis{e1,e2,···,en}.Suppose that

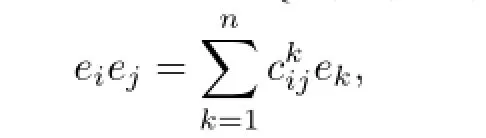
whereare the structure constants.Then any Rota-Baxter operatorRcan be presented by a matrix(rij),whereMoreover,rijsatisfes the following equations(see[7]):

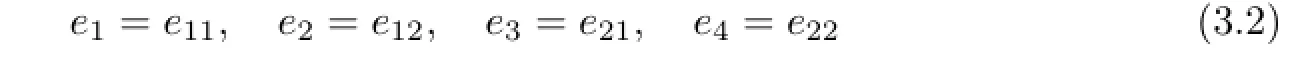
Let be a basis ofM2(F).Sinceeijekl=δjkeil,

We need to compute 4×4-matrix(rij)to obtainR∈RB(M2(F)).BecauseRis a linear operator,we only check that all basis elements satisfy the following identity:

Whenx,yare substituted bye1,e2,e3,e4,respectively,we can obtain the following identities:

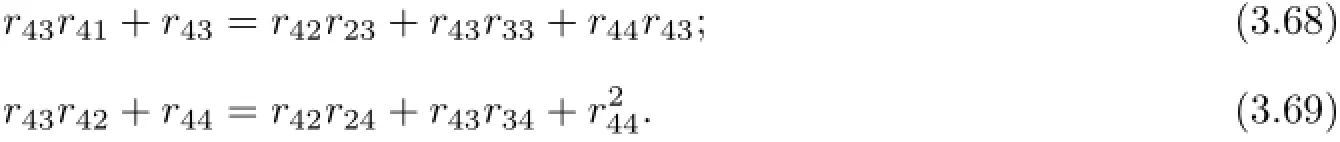
4 Proof

Now,we prove Theorem 2.1.Whenr23=0,it can be obtained thatr21r24=0 by(3.26). In order to solve the equations(3.6)-(3.69),it sufces to compute(rij)in the following fve cases:

4.1Case 1.r23=r24=0,r21/=0.

Case 1.1.r13/=0.We haver43=r12=0,r21=-r13,r32=0,r22+r33=1,r31=0, r11=0 or 1 by(3.6),(3.7),(3.12),(3.16),(3.24),(3.32)and(3.42).

Case 1.1.1.r11=0.We have

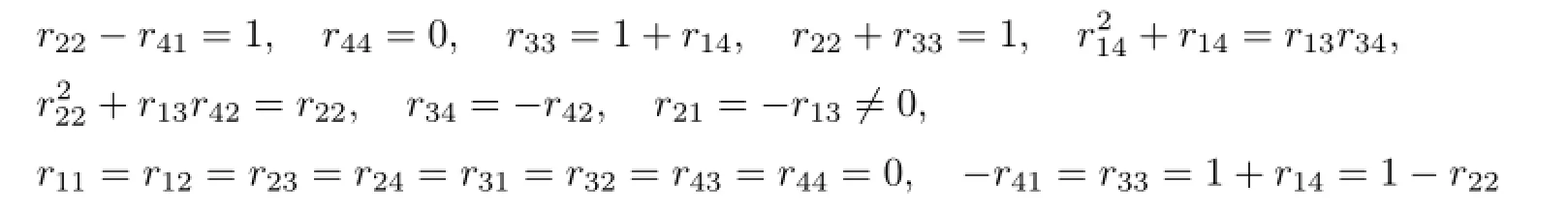
by(3.8)-(3.11),(3.32)and(3.34).Letr13=a/=0,r14=b.We getR1in Theorem 2.1, where

Case 1.1.2.r11=1.We conclude thatI-R1is inRB(M2(F))by Lemma 3.1.

Case 1.2.r13=0.We get

by(3.10),(3.13),(3.44),(3.48),(3.52),(3.54),(3.56)-(3.61).

Case 1.2.1.r43/=0.We getR2in Theorem 2.1 by(3.44),(3.48),(3.52),(3.54),(3.56)-(3.61)and(3.69).

Case 1.2.2.r43=0,wherer13=r14=r23=r24=r43=0,r11+r22=1,r21/=0.It is not difcult to obtainr33=0 or 1 by(3.40).

(A)r33=0.From(3.18),(3.69),we directly conclude thatr12=-r42andr44=0 or 1.

According tor44=0 andr44=1,respectively,we obtainR3andR4in Theorem 2.1 by (3.10),(3.30),(3.34),(3.35),(3.45)and(3.63).

(B)r33=1.We conclude thatI-R3andI-R4are inRB(M2(F))by Lemma 3.1.

4.2Case 2.r21=r23=0,r24/=0.

Case 2.1.r13/=0.We obtain

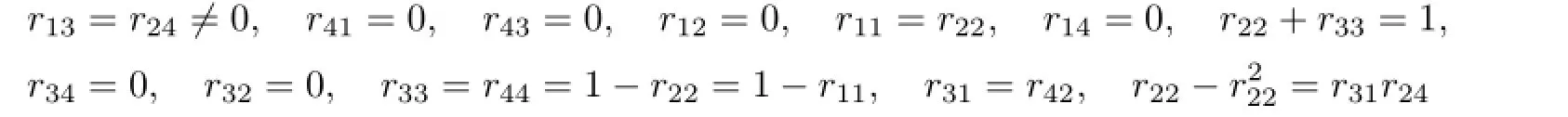
by(3.10),(3.12),(3.16),(3.22),(3.24),(3.25),(3.32),(3.33),(3.43),(3.45),(3.54)and(3.56).

Letr11=a,r13=b/=0.We getR5in Theorem 2.1.

Case 2.2.r13=0.It is not difcult to obtainr11=0 or 1 by(3.6).

Case 2.2.1.r11=0.It is easy to knowr22=1+r14by(3.13).

(A)r43/=0.We getR6in Theorem 2.1 by(3.9),(3.30),(3.37),(3.44),(3.48),(3.52), (3.60),(3.68)and(3.69).

(B)r43=0.We can getr214+r14=r12r24,r22=r222+r24r42,r12=-r42,r41=0, r22+r44=1,r33=0 or 1 by(3.9),(3.35),(3.34),(3.37)and(3.40).

According tor33=0 andr33=1,respectively,we obtainR7andR8in Theorem 2.1 by (3.17),(3.30),(3.39)and(3.45).

Case 2.2.2.r11=1.We conclude thatI-Riare inRB(M2(F))(i=6,7,8)by Lemma 3.1.

4.3Case 3.r23=r21=r24=0.

We can obtainr13=0,r43=0 andr33=0 or 1 by(3.24),(3.40)and(3.60).

Case I.r33=0.It is easy to getr11=0 or 1 by(3.6).

(I)r11=0.We can obtainr22=0 or 1 by(3.11).

(I.1)r22=0.It is not difcult to obtainr14=0 or 1 from(3.11).

(I.1.1)r14=0.We obtainr12=r31=r32=r34=r41=r42=r44=0 by(3.31),(3.38), (3.39),(3.41),(3.42),(3.43)and(3.45).So we getR9=0in Theorem 2.1.

(I.1.2)r14=-1.We can getr12=0 by(3.31),r14=0 by(3.33),which is inconsistent withr14=-1.Hence,the system of the equations(3.6)-(3.69)has no solution in this case.

(I.2)r22=1.By(3.7)and(3.9),we can getr12r14=0 andr14=0 or-1.

(I.2.1)r14=0.We can getr44=0 or 1 from(3.69).

(A)r44=0.It is not difcult to obtainr34=0 from(3.65),r41=0 or-1 from(3.66).

Byr41=0 andr41=-1,respectively,we getR10andR11in Theorem 2.1.

(B)r44=1.Similarly,we obtainR12andR13in Theorem 2.1.

(I.2.2)r14=-1.In the same way,we getR14andR15in Theorem 2.1.

(II)r11=1.Herer13=r21=r23=r24=r33=r43=0 andr22=0 or 1.

(II.1)r22=0.We can getr11=0 from(3.30),which is inconsistent withr11=1. Hence,the system of the equations(3.6)-(3.69)has no solution in this case.

(II.2)r22=1.From(3.7)and(3.9),we can concluder12r14=r12andr14=0 or 1. (II.2.1)r14=0.We can getr44=0 or 1.

(A)r44=0.We getr41=0 or-1 by(3.66)and we getR16andR17in Theorem 2.1.

(B)r44=1.Similarly,we getR18andR19in Theorem 2.1.

(II.2.2)r14=1.In the same way,we getR20andR21in Theorem 2.1.

Case II.r33=1.We conclude thatI-Ri(i=9,10,···,21)are inRB(M2(F))by Lemma 3.1.

4.4Case 4.r23/=0,r12=0.

We have

by(3.20),(3.21),(3.28),(3.52),and by(3.12),(3.36),we get

It is easy to getr22=0 or 1 by(3.11).

Case 4.1.r22=0.

Case 4.1.1.r14/=0.We haver31=0,r41=0 andr11=0 or 1 by(3.17),(3.21)and (3.6).

(B)r11=1.Similarly,we getR24andR25in Theorem 2.1.

Case 4.1.2.r14=0.From(3.25),(3.69),we concluder34=0 andr44=0 or 1.

(A)r44=0.We can getr11=-r41by(4.1)andr24=0 by(3.37).According tor13/=0 andr13=0,respectively.We getR26andR27in Theorem 2.1 by(3.6),(3.8),(3.10),(3.12), (3.22),(3.24)and(3.36).

(B)r44=1.Similarly,we getR28andR29in Theorem 2.1.

Case 4.2.r22=1.We conclude thatI-Ri(i=22,23,···,29)are inRB(M2(F))by Lemma 3.1.

4.5Case 5.r23/=0,r12/=0.

We have

by(3.7),(3.8),(3.10),(3.12)-(3.14),(3.21),(3.23),(3.27),(3.28),(3.36)and(3.68).r14+r44=0 or 1 from(3.6).

Case 5.1.r14+r44=0.We have(r13r14-r12r23)(r14r23-r13r24)=0 by(3.37).

Case 5.1.1.r13r14=r12r23.Letr12=a,r13=b,r14=c.We getR30in Theorem 2.1 by(3.50).

Letr12=τ,r13=a,r14=b,r23=c.We getR31in Theorem 2.1 by(3.10),(3.21),(3.23), (3.25),(3.29),(3.32),(3.62)and(3.68).

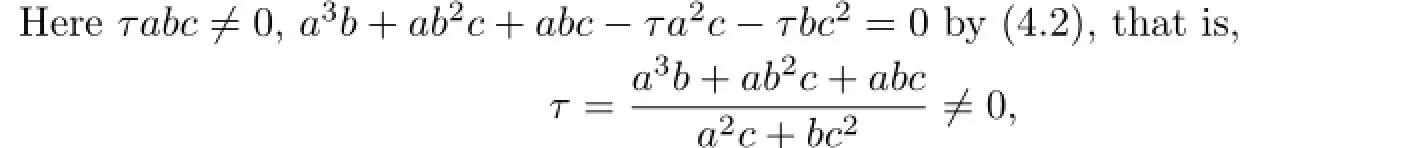
whereabc/=0.In fact,we havea3b+ab2c+abc/=0 anda2c+bc2/=0 by(3.12)and(3.69).

Case 5.2.r14+r44=1.We conclude thatI-R30andI-R31are inRB(M2(F))by Lemma 3.1.

[1]Baxter G.An analytic problem whose solution follows from a simple algebraic identity.Pacifc J.Math.,1960,10:731-742.

[2]Rota G C.Rota-Baxter algebras and combinatorial identities I.Bull.Amer.Math.Soc.,1969,75:325-329.

[3]Guo L.What is a Rota-Baxter algebra?Notice Amer.Math.Soc.,2009,56:1436-1437.

[4]Guo L,Keigher W.Free commutative Rota-Baxter algebras and shufe products.Adv.Math., 2000,150:117-149.

[5]Guo L,Ebrahimi-Fard K.Free noncommutative Rota-Baxter algebras and rooted trees.J.Algebra Appl.,2008,7:167-194.

[6]Miller J B.Baxter operators and endomorphisms on Banach algebras.J.Math.Anal.Appl., 1969,25:503-520.

[7]An H H,Bai C M.From Rota-Baxter algebras to pre-Lie algebras.J.Phys.A,2008,41: 015201-015219.

[8]Li X X,Hou D P,Bai C M.Rota-Baxter operators on pre-Lie algebras.J.Nonlinear Math. Phys.,2007,14:269-289.

A

1674-5647(2015)01-0071-10

10.13447/j.1674-5647.2015.01.08

Received date:Jan.7,2013.

Foundation item:The NSF(JC201004)of Heilongjiang Province and the NSF(11171055)of China.

*

.

E-mail address:lijinzhi800213@163.com(Li J Z),wendeliu@ustc.edu.cn(Liu W D).

2010 MR subject classifcation:16A06,47B99