一类曲线图形数据挖掘的数值算法及其实现*
宋花玉
(陕西省委党校 科技部,西安710061)
在工程实际中,经常遇到一类以曲线图形形式只给出部分数据要求其余数据的问题.如航空工程中根据发动机在几个典型压力高度上的推力曲线图,确定发动机在其它任意压力高度、任意速度的推力,土建工程中,根据石灰土在几个典型龄期的强度曲线图,确定石灰土在其它任意龄期、任意混合比的强度.这类问题在工程实际中的传统处理方法是先通过人工作图查找相关数据再用两点插值进行计算[1-2].这种方法速度慢,精度低,不能用于大规模的精确计算问题.对于这类曲线图形数据的大规模精确计算问题,文献[3-7]进行了探索,提出了一些计算方法.文献[3-5]提出的“就近整体拉格朗日拟合算法”,以距计算点最近的三条曲线为基础,利用多次一元拉格朗日插值拟合出计算点所在的整条曲线的函数规律,利用此函数确定计算点的对应值.这种方法的插值节点间距较大,根据插值的误差理论[8],这种方法的计算结果误差较大.文献[6-7]提出的“就近小区域二元拉格朗日拟合算法”,利用就近原则,在已给曲线上找出与计算点最接近的9个点,以这9个点为插值节点,利用二元拉格朗日插值拟合出计算点所在小区域的函数规律,然后利用此函数确定计算点的对应值.由于插值节点取在计算点的附近,在一般情况下,这种方法比文献[3-5]的就近整体拟合算法准确.但这种方法也存在一定的缺陷,由于二元9点插值多项式的次方较高,当曲线比较陡峭时,这种方法的计算结果不稳定,在插值过程中容易出现“龙格”现象.而且文献[3-7]均未对所研究的这类曲线图形的数据特征进行分析,也未进行误差估计,只是利用所提方法对所研究的具体问题进行了计算.文中对此问题进行了一般性的研究,分析曲线图形所表示的数据关系是一种二元函数关系,提出一种准确稳定的通用数据挖掘算法.
1 插值算法及误差分析
1.1 数据特征分析和插值算法
文献[1-7]中的问题可以统一表示为:设在某变化过程中有三个变量x、y和z,变量z的值由变量x和y的值确定,但具体关系式未知.图1中的m条曲线Ci(i=1,2,…,m)给出了当变量x在m个值x=xi(其中xi为常数,i=1,2,…,m)中任取一值,变量y在一定区间内任取一值时变量z的对应值,据此求当变量x在一定区间内任取一值x*,变量y在一定区间内任取一值y*时变量z的对应值.图1中,横轴表示变量y,v1,v2,…v,k为横轴y刻度值,且v1<v2<…<vk;纵轴表示变量ω1,ω2,…,ωr为纵轴z的刻度值,且ω1<ω2< …<ωr.
研究分析可得如图1所表示的数据有以下特征
① 变量x和y一旦取定,变量z值就唯一确定.
②m条曲线均无“峰”无“谷”,由此可知当变量x固定时,变量z关于变量y是单调的,所以不会出现这样的情况:x相同而y不同的两对数对应的z相等.
③m条曲线没有交点,即当变量y固定时,变量z关于变量x是单调的,所以不会出现这样的情况:y相同而x不同的两对数对应的z相等.
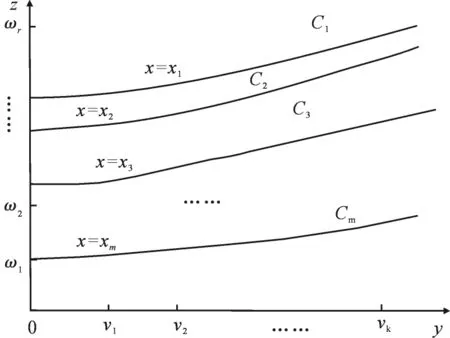
图1 曲线数据示意图Fig.1Graph of curve data
由特征①可知变量z是变量x和y的二元函数,记作z=f(x,y),再由特征 ②、③ 可知此二元函数是一一对应的,文献[1-7]中的问题变为已知二元一一对应连续函数z=f(x,y)在如图1所示的m条无“峰”无“谷”且互不相交的曲线x=xi(i=1,2,…,m)上的函数值,求z=f(x,y)在任意点(x*,y*)的函数值.
根据变量z关于变量y和x分别是单调的特征,可以把这个二元函数值的确定问题转化为一元函数的插值问题.基本思路为:①固定变量y,将二元函数z=f(x,y)变为关于x的一元函数,用一元插值对其进行相关的计算,得到需要的计算结果;② 固定变量x,将二元函数z=f(x,y)变为关于y的一元函数,以第一步所得结果为条件,用一元插值对此关于y的一元函数进行插值计算便可得到结果.由于变量z关于变量y和x分别是单调的,这就保证了一元插值能够顺利有效的进行.以下给出本文通过插值确定z=f(x,y)在图中范围内任意点(x*,y*)的函数值的具体步骤为
①采集基础数据,在图1的横轴上从坐标原点开始以足够小的步长τ取值y0=0,y1=τ,y2=2τ,…,yn=nτ(其中n由图形中y轴的最大标度确定),把图中每条曲线中包含的函数值按第二个变量y每隔τ查找并记录下来,设查出的在第一个变量为xi,第二个变量为yj时的函数值为zij,i=1,2,…,m,j=0,1,2,…,n.
② 从x=x1,x=x2,……,x=xm中寻找出与x*最接近的3个,假设这3个为x1、x2、x3,它们对应的图1中的曲线分别为C1、C2、C3;从y0=0、y1=τ、y2=2τ、…、yn=nτ中寻找出与y*最接近的2个,假设这三个为y1=τ、y2=2τ;
③ 在函数z=f(x,y)中固定第二个变量y的值为y1=τ,从基础函数值数据中找出曲线C1、C2、C3上与y1=τ对应的函数值z11、z21、z31,以x1、x2、x3为插值节点,以(x1,z11)、(x2,z21)、(x3,z31)为插值条件,利用拉格朗日插值公式可得在第二个变量y固定为常值y1=τ,第一个变量x在区间[x1,x3]上时函数z=f(x,y)与第一个变量x的2次多项式插值拟合函数f1(x)

④ 将x=x*代入式(1),可得二元函数z=f(x,y)在第一个变量x取x*,第二个变量y取y1=τ时的2次多项式插值拟合函数值f1(x*)

⑤ 在函数z=f(x,y)中固定第二个变量y的值为y2=2τ,从基础函数值数据中找出曲线C1、C2、C3上与y2=2τ对应的函数值z12、z22、z32,以x1、x2、x3为插值节点,以(x1,z12)、(x2,z22)、(x3,z32)为插值条件,利用拉格朗日插值公式可得在第二个变量y固定为常值y2=2τ,第一个变量x在区间[x1,x3]上时函数z=f(x,y)与第一个变量x的2次多项式插值拟合函数f2(x)

⑥ 将x=x*代入式(2),可得二元函数z=f(x,y)在第一个变量x取x*,第二个变量y取y2=2τ时的2次多项式插值拟合函数值f2(x*)
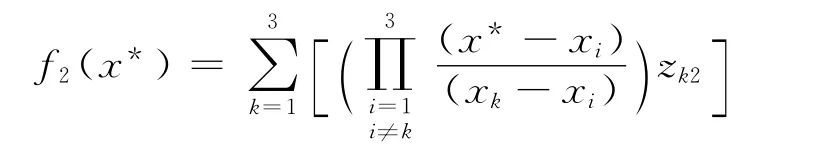
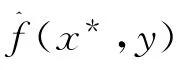
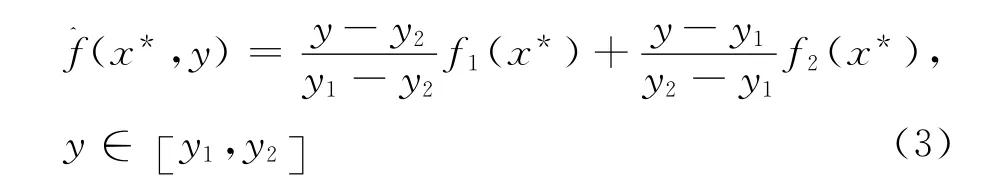
⑧ 将y=y*代入式(3),便可得到二元函数z= f(x,y) 在 点 (x*,y*) 处 的 拟 合 函 数 值

1.2 算法选取依据及误差分析
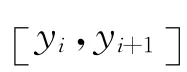

由式(5)可知,插值点x在插值节点x1、x2、x3某点附近时,2次插值的误差较小,插值点x离插值节点x1、x2、x3越近,二次插值的误差越小.因为我们要计算式(1)中当x=x*时的函数值拟合,为了减少误差,所以在1.1插值算法的具体步骤 ②中要从x=x1,x=x2,……,x=xm中寻找出与x*最接近的3个.

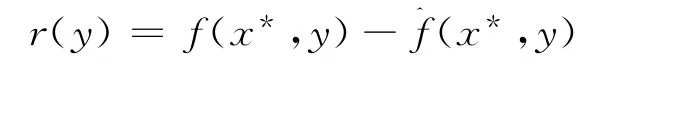

2 算法实现及实例计算


图2 检验曲线图Fig.2 Testing curve graph
为了检验文中算法,取图2中与x=2 000m对应的曲线C3为检验曲线,在其上取10个点(见表1第1列),用文中程序计算这10个点的函数值(因为做检验之用,所以计算时应该把从曲线C3采集到的11个基础函数值从程序的基础数据文本文件中暂时去掉),并与从图上查出的准确函数值进行对比,结果见表1.
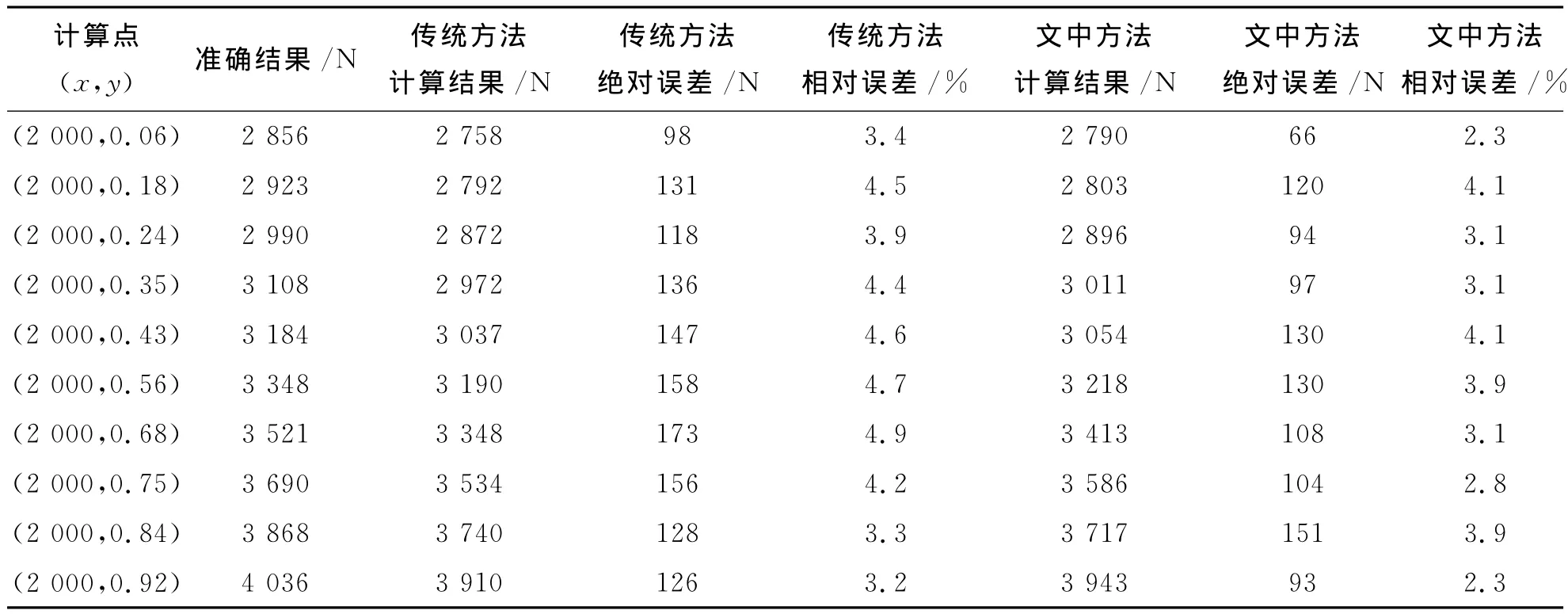
表1 计算结果检验数据Tab.1 Testing data of calculation result
从表1的第2列和第6列数据可看出,程序计算得到结果与图中查出的准确结果基本吻合.计算可知,程序计算结果与准确结果的平均绝对误差为109N,平均相对误差为3.3%,根据问题的实际意义,这样的误差在小于5%的误差允许范围之内,这说明本文提出的算法在实际中是准确可行的.
从理论上说,传统方法只用到计算点附近的3个插值节点的函数值,而本文算法用到计算点附近的9个插值节点的函数值,文中的算法更接近于函数的真实状态,所以本文的计算结果精度更高.实际计算结果也证明了这一点.在本例中,用传统方法计算所取10个点的函数值,并与从图上查出的准确函数值进行对比,结果见表1.计算可知,传统方法计算结果的平均相对误差为4.1%,比本文程序计算结果的平均相对误差大0.8%.在本例中经多次实际计算可知,传统方法进行一次计算需要10min左右,文中程序进行1次计算所需时间不超过2s,所以文中算法效率更高.
3 结 论
1)对一类曲线图形的数据挖掘进行了研究,在分析这类曲线图形的数据关系是二元函数的基础上,提出就近小区间拉格朗日插值挖掘算法.
2)实例计算表明,本文算法的平均相对误差为3.3%,传统算法的平均相对误差为4.1%,文中算法比传统算法准确,利用传统方法进行1次计算需要10min左右,利用文中程序进行1次计算所需时间不超过2s.
3)文中算法虽然是对具有图1数据特征的曲线图形的数据挖掘设计的,但对于其他的一般曲线图形的数据挖掘,在对曲线图形进行一定的分割后,仍可用文中算法.当曲线图形有“峰”有“谷”,或相互交叉时,应从“峰”、“谷”、“交叉点”处分开,转化为一段一段无“峰”无“谷”无“交叉点”的情形,这时在每一段内曲线图形具有图1数据特征.
[1] 邓学均.路面路基工程[M].北京:人民交通出版社,2008.DENG Xue-jun.Pavement and Subgrade Construction[M].Beijing:China Communications Press,2008.(in Chinese)
[2] 洪冬林.石灰稳定土最大干密度与龄期的关系[J].铁道建筑技术,2011,28(3):57.HONG Dong-lin.Relationship between Lime Stabilized Soil’s Maximum Dry Density and Its Age[J].Railway construction technology,2011,40(3):57.(in Chinese)
[3] 宋花玉.飞机起飞滑跑发动机推力数值确定方法[J].航空计算技术,2010,40(6):43.SONG Hua-yu.A Numerical Value Confirmation Method of Engine Thrust in Aircraft Take-off Running[J].Aeronautical Computing Technique,2010,40(6):43.(in Chinese)
[4] 金星驰,龚光军,董玉德.图形生成与变换算法可视化的原理与方法(英文)[J].西安工程大学学报,2014,28(01):94.JIN Xing-chi,GONG Guang-jun,DONG Yu-de.The Principle and Method of Graphics Generating and transform Algorithm Visualization(in English)[J].Journal of Xi’an Polytechnic University,2014,28(01):94.(in Chinese)
[5] 杨旭,董玉德,余来宏,等.图形自动编程在火焰切割机系统开发中的实现[J].西安工程大学学报,2014,28(2):235.YANG Xu,DONG Yu-de,YU Lai-hong,et al.Realization of Graphic Automatic programming in Flame Cutting Machine System[J].Journal of Xi’an Polytechnic University,2014,28(2):235.(in Chinese)
[6] 宋花玉,蔡良才.飞机起飞航迹计算中发动机推力计算方法[J].交通运输工程学报,2010,10(2):59.SONG Hua-yu,CAI Liang-cai.Computational Method of Engine Thrust in Aircraft Take-off Track Calculation[J].Journal of Traffic and Transportation Engineering,2010,10(2):59.(in Chinese)
[7] 宋花玉.飞机起飞性能计算中发动机推力确定方法的改进[J].航空计算技术,2015,45(1):61.SONG Hua-yu.Improvement of Engine Thrust Confirmation Method in Aircraft Take-off Performance Calculation[J].Aeronautical Computing Technique,2015,45(1):61.(in Chinese)
[8] 黄云清.数值计算方法[M].北京:科学出版社,2010.HUANG Yun-qing.Numerical Computation Method[M].Beijing:Science Press,2010.(in Chinese)
[9] 朱金付.C++实验指导书[M].北京:清华大学出版社,2009.ZHU Jin-fu.C++ Experiment Instruction[M].Beijing:Tsinghua University Press,2009.(in Chinese)

