运用Foveated非局部均值和局部核回归的单幅图像超分辨重构＊

吴玉莲，张文娟

（1．西安医学院 卫生管理系，西安710021；2．西安工业大学 理学院，西安710021）

图像超分辨重构是通过从同一场景获取的一幅或几幅低分辨图像产生一幅高分辨率图像的过程．高分辨率图像在很多实际问题中经常用到，由于图像摄取设备和环境的局限性，很难直接获取到高分辨率图像，因此超分辨重构是当前计算技术研究的一个热点［1-3］．

超分辨重构方法之一是基于插值的方法，其基本思想是通过基函数或插值核来估计所需的高分辨率像素．在图像的光滑地区这种方法能达到比较满意的效果，在图像的纹理地区经常会产生可见的伪吉布斯震荡现象．超分辨重构的另一种方法是基于例子学习的方法［1-2］，此方法假设低分辨图像中失去的高分辨率细节可通过一些低分辨图像和相应的高分辨率图像学习获取．然而通过不适合的训练抽样产生的高分辨率图像边界地区经常产生一些虚假现象．超分辩重构的第三种方法是基于某种经验的重构的方法．此问题需要一些正则化先验假设来完成高分辨率重构．一些不同的先验已经被用到此方法中，比如用于保边的基于梯度的先验［3］，基于非局部的正则化先验［4］用来保边和压制虚假现象．自然图像的一个特性是局部光滑性，它的局部结构是相当稳定的．因此可以用比如标准化卷积，双边滤波，引导核回归［5-6］等局部方法描述一个像素，即其可以表示为局部邻域的加权平均．其中引导核回归这种局部方法由于自适应于图像的局部结构的鲁棒性而呈现很好的恢复效果．自然图像的另一个特性是局部图像块的非局部相似性，代表性的工作是传统的非局部均值滤波［4］及基于Foveated相似性的非局部滤波［7］．文献［7］的去噪实验结果表明比起传统的加窗非局部均值滤波，基于Foveated相似性的非局部滤波取得了更好的去噪质量和视觉效果，原因在于基于Foveated自相似性比传统的基于加窗的自相似性能更加合理的刻画图像的非局部特性．Foveated非局部相似性考虑局部图像块的冗余性和人类视觉的基本原理，图像的局部结构正则性使重构的高分辨率图像愈发稳定．为此，文中利用自然图像的Foveated非局部相似性和局部结构正则性以得到高分辨图像，联合运用自然图像的这两个互为补充的正则化先验进行高分辨率重构，以期获得高质量的高分辨率重构图像．

1 Foveated非局部均值及引导核回归

对于Foveated非局部均值，不同图像块之间的相似性用Foveated距离代替传统的加窗距离．具体而言，计算Foveated距离的图像块首先被逐渐增加的标准差（随着远离块中心像素点）点扩散函数模糊．假设图像恢复的一般模型为

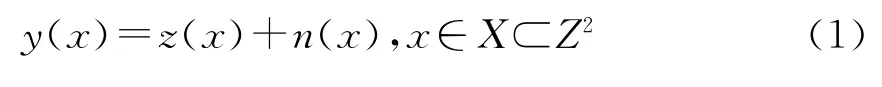
式中：X∈Z2为图像域；y为观测图像；z为未知的干净图像；n为高斯白噪声．数学上，Foveated非局部均值定义为

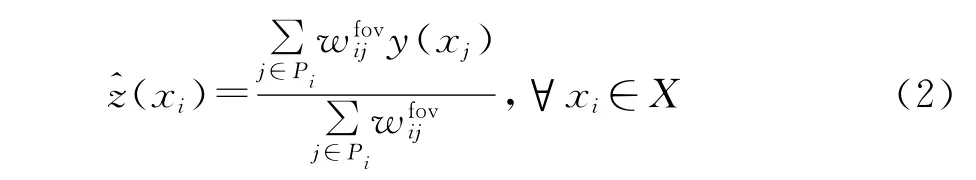
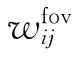
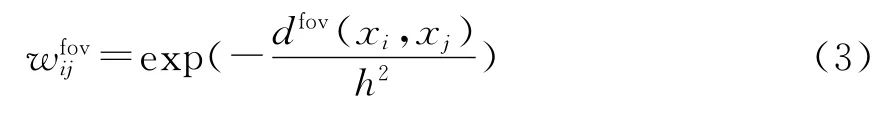
式中：h为全局光滑性参数．Foveated距离定义为

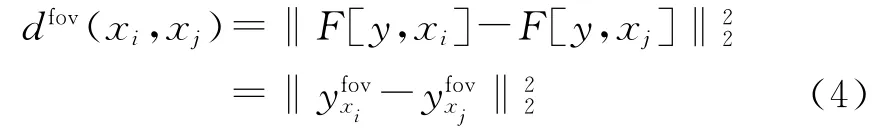
式中：F为Foveation算子．给定图像y和像素点x，Foveated块yfov：U→R，U 是中心在圆点的一个邻域，则

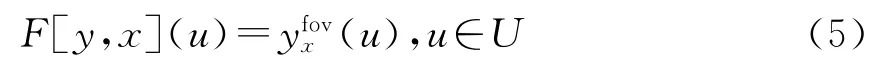
算子F是标准差逐渐增加的空域模糊算子．Foveation算子F的详细设计参见文献［7］．

引导核回归［5］是图像恢复中最受关注的方法之一，基本思想是目标像素表示来自其附近一组像素的回归权的加权平均．被估计图像z中点xi处的估计值为

式中：矩阵Ci为xi点处水平方向和垂直方向的对称梯度协方差；hk为控制引导核支撑范围的光滑参数；上标T为转置算子．

2 基于Foveated非局部均值滤波和引导核回归的超分辨

从单幅低分辨率图像获取高分辨图像模型为

式中：Y为初始低分辨图像；X为未知的高分辨图像；H和D分别为模糊和下采样算子；σ为零均值的高斯白噪声．超分辨重构图像获取目的就是用低分辨图像Y得到高分辨的图像X．

由于模糊和下采样算子的影响，一幅低分辨图像可能对应着很多不同的高分辨图像，所以超分辨重构图像获取本质上是偏态的．为使其变为良态的，必须施加一些先验正则化条件，假设正则项为Ri（X），那么高分辨目标图像X的MAP估计为

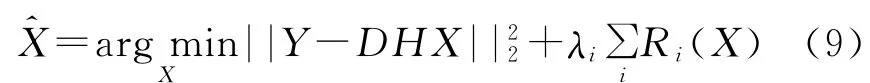
其中λi为正则性参数，用来平衡不同正则项与重构误差项．

文中将Foveated非局部均值滤波正则项代替传统非局部均值滤波项，亦期待更好的超分辨图像重构结果［6］．对于Foveated非局部均值正则项，文中采纳Foveated非局部均值滤波来反映图像中的非局部相似性．每个目标像素都可再现为与之相似邻域像素的加权平均，即

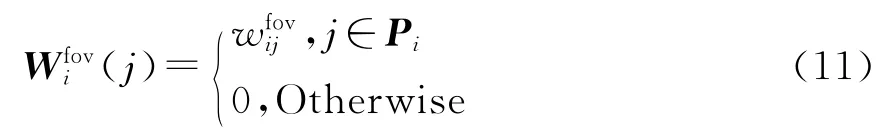
其中Pi为以i为中心的邻域像素指标形成的列向量．根据自然图像的这种Foveated非局部相似性，其加权均值和所求高分辨图像X的误差要尽可能小，因此Foveated非局部正则项为

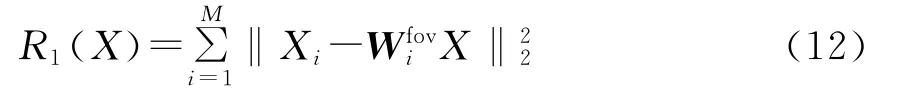
其中M为X中像素的个数．可以简化为

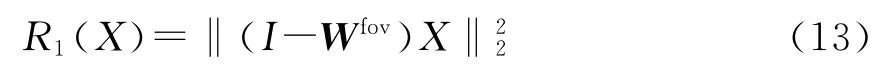
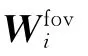
对于引导核回归相似正则项，按照与式 （12）相似的原理，可以写为

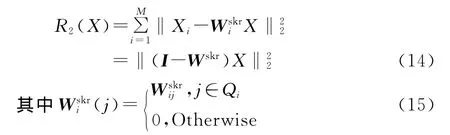
式中：Qi为引导核回归滤波中以i为中心的邻域像素指标形成的列向量；Wskr为由Wskri定义的引导核回归权矩阵．

组合正则项式（13）和式（14），文中的超分辨率模型为

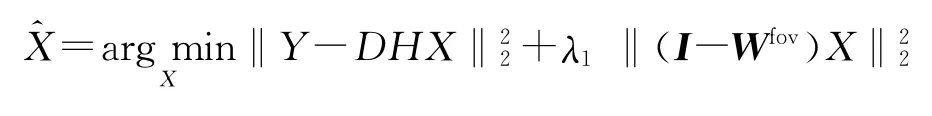
根据梯度下降迭代算法，式（16）写为

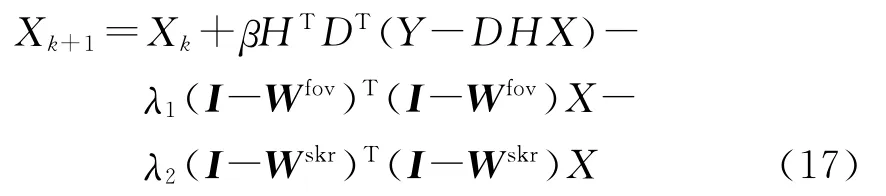
其中β为梯度下降迭代参数．在进行迭代算法之前，先对低分辨图像进行双三次插值预处理，然后迭代式（17）直到满足给定的条件．

3 数值实验及分析

为了验证文中算法的有效性，分析取自分割图像库BSDS300［8］的10幅不同的自然图像，并与双三次插值方法和文献［6］方法进行了比较．文中用峰值 信 噪 比 （The Peak Signal to Noise Ratio，PSNR）和结构相似性指标（Structural Similarity，SSIM）来估计最后重构的超分辨图的质量．实验中将原有高分辨图像放大3倍后采样并经高斯核模糊模拟得到要处理的低分辨图像，超分辨重构仅处理彩色图像的亮度部分．上述三种方法处理10幅实验图像得到的PSNR和SSIM见表1，其中第一行和第二行分别为每幅图像的PSNR和SSIM值．双三次插值直接调用Matlab插值函数．从表1看出，双三次插值重构效果量值远低于后两种方法，文献［6］方法和文中方法都取得了比双三次插值更好的重构效果量值．文中方法的平均PSNR比文献［6］方法高0．18dB，SSIM 比文献［6］方法高0．004．在上述三种方法中，文中方法的重构效果量值最优．

为了比较不同方法高分辨重构图像的视觉效果，Butterfly，Bike和Plants三幅图像重构结果如图1所示，图1中从左向右第一列为低分辨图像，第二列为双三次插值放大图像，第三列为文献［6］方法的放大图像，最后一列为文中方法的放大图像．图2为图1的局部放大图．从图1可以看出，双三次插值得到的图像比较模糊，文中方法重构的图像比文献［6］方法产生更少的额伪边界效应，保持了更多的纹理细节和更好的边界，这些都能从图2中观察到．图2中从左向右第一列为理想局部放大图像，第二列为双三次插值的局部放大图像，第三列为文献［6］方法的局部放大图像，最后一列为文中方法的局部放大图像．对比图2的Butterfly和Plants局部放大图像，文中方法得到的图像边界更接近理想的高分辨率图像，Bike图像的字母经文中方法重构后图像较其他两种方法清晰．

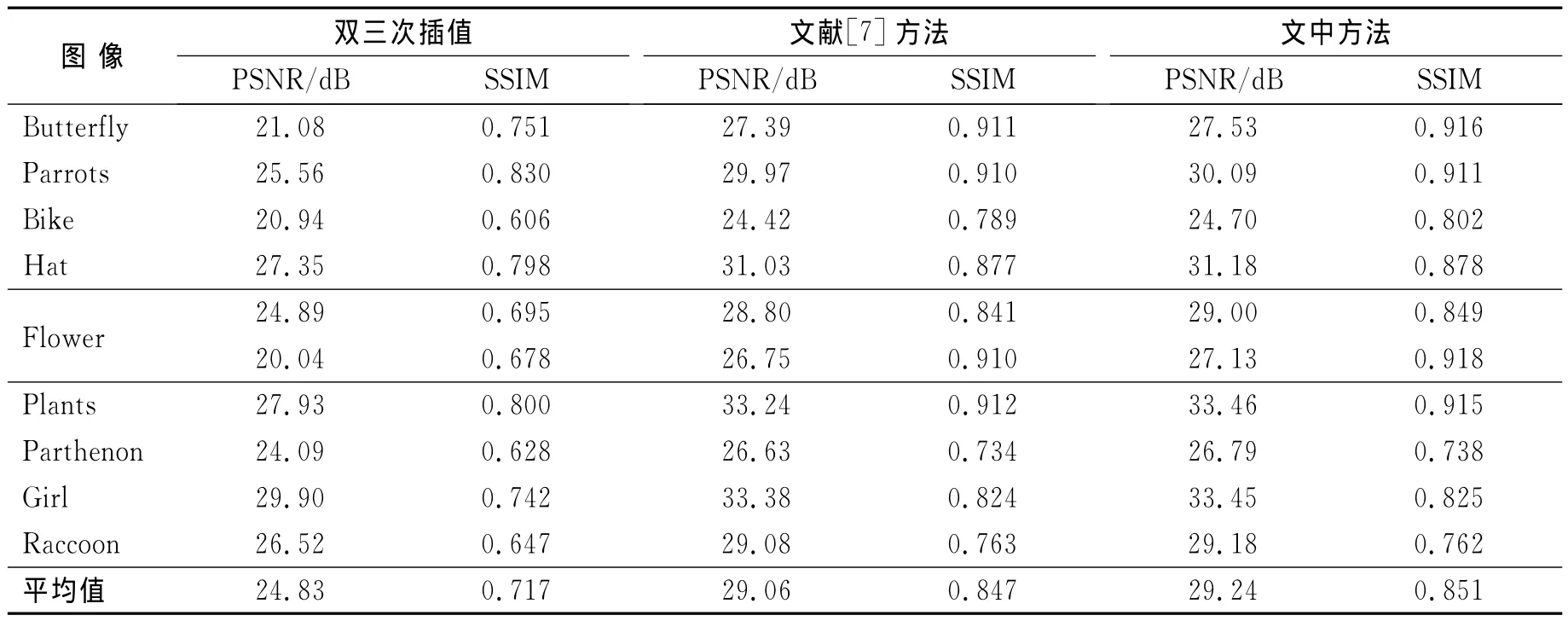
表1 不同方法处理放大3倍后的实验图像得到的PSNR和SSIMTab．1 Composition of PSNR （dB）and SSIM results obtained by different methods for 3×magnification

图1 双三次插值、文献［7］方法和文中新方法对三幅图像的重构比较Fig．1 Comparison befween the three test images obtained by the Bicubic method，the method from ［7］and the proposed method

图2 不同的局部放大图像的比较Fig．2 Comparison with the three different local magnifications for three test images

4 结 论

由于全局重构限制，Foveated非局部块相似性及局部核回归给出一致的迭代极小化超分辨模型，通过梯度下降法求解该模型，结合自然图像的实验结果从峰值信噪比、结构相似性指标及视觉效果上均验证了一致的迭代极小化超分辨模型的有效性．该超分辨模型实现了将Foveated非局部块相似性冗余扩展到多尺度的非局部相似性块冗余．对Foveated非局部相似性仍需在今后进一步深入研究，以将其推广到更广泛的应用中．

［1］ FREEMAN W T，JONES T R，PASZTOR E C．Example Based Super Resolution ［J］．IEEE Computer Graphics and Applications，2002，22（2）：56．

［2］ ELAD M，DATSENKO D．Example-based Regularization Deployed to Super-resolution Reconstruction of A Single Image［J］．Computer Journal，2009，52（1）：15．

［3］ SUN J，XU Z B，SHUM H Y．Gradient Profile Prior and Its Applications in Image Super-Resolution and Enhancement［J］．IEEE Transactions on Image Processing，2011，20（6）：1529．

［4］ BUADES A，COLL B，MOREL J M．A Review of Image Denoising Algorithms with a New One［J］．Multiscale Modeling ＆Simulation，2005，4（2）：490．

［5］ TAKEDA H，FARSIU S，MILANFAR P．Kernel Regression for Image Processing and Reconstruction［J］．IEEE Transactions Image Processing，2007，16（2）：349．

［6］ ZHANG K B，GAO X B．Single Image Super-Resolution with Non-Local Means and Steering Kernel Regression ［J］．IEEE Transactions on Image Processing，2012，21（11）：4544．

［7］ ALESSANDRO F，GIACOMO B．Foveated Self-similarity in Nonlocal Image Filtering［C］／／Processing SPIE Electronic Imaging 2012．Burlingame：Human Vision and Electronic Imaging XVII，2012：829110．

［8］ MARTIN D，FOWLKES C，TAL D．A Database of Human Segmented Natural Images and Its Application to Evaluating Segmentation Algorithms and Measuring Ecological Statistics［C］／／Processing International Conference Computation Vision．Vancouver：IEEE，2001：416．