高强双角钢十字截面构件承载力折减系数

杨隆宇

(中国电力工程顾问集团华北电力设计院有限公司，北京 100120)

高强双角钢十字截面构件承载力折减系数

杨隆宇

(中国电力工程顾问集团华北电力设计院有限公司，北京 100120)

双角钢十字截面构件承载力设计值与真型塔试验不符，目前对此问题的研究多集中于对现象的描述，不够深入。同时，现广泛使用的计算模型可推导出自相矛盾的结论，这给构件设计带来很大困惑。为研究承载力差异的产生原因，对常用规格双节间双角钢构件进行构件试验。通过对试验结果的分析，建立考虑弯曲、翘曲、扭转等因素的理论计算模型，并用能量原理和里茨法得到构件在两种典型屈曲模式下的柱子曲线。结果表明，考虑整体和局部稳定的计算模型能较好地与试验结果吻合;两种屈曲模式下双角钢构件承载力的差异可达10%以上。以此为基础分析现有设计方法的不足，给出考虑不同角钢宽厚比的建议承载力计算公式。建议公式为试验值的下限，可为此类构件计算提供参考。

高强钢;双角钢十字截面;承载力;能量原理;折减系数

0 引言

随着特高压建设的不断发展，导线荷载和铁塔高度不断增加，对输电塔构件承载力提出更高要求。目前特大规格角钢相关标准不完善，生产、加工、采购困难，配套的螺栓等附件也有待进一步研究;Q420及以上高强钢在复杂气象区应用有诸多限制，还无法发挥其应有作用。因此，研究组合截面构件对保障电网运行、优化线路经济指标具有十分重要的意义［1，2］。

国内外对此类构件的研究逐步增多［3～7］，但目前规范［8，9］中双角钢十字截面构件的相关条文不够详细，在真型塔试验中发现构件承载力的试验值与计算值相比明显偏低［10］。现有学者的研究［11～13］对这种组合截面构件计算方法的研究不够深入。双角钢十字截面扭转刚度参数较小，实际构件在发生弯曲变形的同时还伴随着扭转变形。本文为分析真型塔试验与计算值偏差产生原因，采用高强钢的双角钢十字截面构件进行试验，并以此建立计算模型，用能量法求解构件屈曲荷载，得到可应用于工程设计的建议计算方法。

1 试验研究

由于铁塔支撑方式与普通压杆有区别，为研究组合截面构件承载力，试验采用Q420钢材的L160×14角钢组成双角钢十字截面构件，沿相互垂直的两肢方向设置L70×5角钢为横向支撑，构件长细比分级30→35→40→45→50。试验装置简图如图1所示。

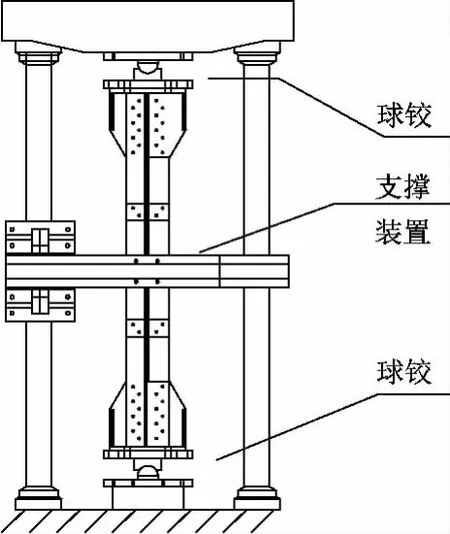
图1 试验装置图

每个选定的组合截面上布置8个应变片，逐级加载，待稳定后用动态应变仪记录与荷载对应的应变。为研究两方向横向支撑对构件承载力的影响，在每个横向支撑和钢梁之间设置200 kN轴力传感器，以记录加载过程中支撑轴力变化 (如图2所示)。

图2 横向支撑传感器

构件承载力、屈曲变形受横向支撑影响很大。从加载到破坏过程中，横向支撑的两种典型受力状态见图3和图4。

图3 横向支撑典型状态I

图4 横向支撑典型状态II

图3(典型状态I)中，横坐标是横向支撑所连应变仪的读数，纵坐标是构件外荷载。两横向支撑所受轴力在加载初期就表现出较大差异;随着外荷载的增加，其中一个横向支撑轴力增长缓慢。在接近屈曲荷载时，两支撑轴力相差可达5倍以上 (即其中一个横向支撑几乎没有对构件承载力的提高做出贡献)。在典型状态II中 (图4)，两横向支撑从加载开始始终共同受力，构件达临界荷载、发生屈曲变形后的荷载－应变曲线变化规律基本一致。

横向支撑的不同工作状态影响构件弯曲屈曲:出现典型状态I，表示构件主要在图5中xoy的坐标轴发生弯曲屈曲;典型状态II，表示构件在x‘oy’的坐标轴弯曲屈曲。当构件以xoy的坐标轴发生弯曲屈曲时，可认为其中一个支撑没有参与受力、没有起到将计算长度减半的作用。受构件初弯曲、加载装置偏心等初始缺陷影响，受力过程中截面的中性轴较难维持与坐标轴重合 (这种情况在典型状态I时最明显)。中性轴移动后，受压肢会在残余应力和轴压力作用下提前翘曲，明显降低整个构件承载力，因此这种情况下截面应按实腹式考虑。由于高强钢应力－应变曲线没有明显的屈服平台、与规范中理想化的双线性模型存在较大差异，因此典型状态I的情况在使用高强钢时更容易发生。

图5 构件截面图

构件在两种典型支撑状态下发生的弯曲屈曲形式如图6所示。

图6中 (a)构件弯曲变形主要集中在下半个节间的弯折处 (构件的其余部分轴线没有明显变化)，角钢受压肢在该处有明显翘曲变形;由于该角钢在弯折处恰好存在平行中性轴的填板，使角钢弯曲变形不连续，导致该角钢上平行中性轴的肢也产生较大局部变形。此种情况下，构件计算长度不应按总长的一半考虑。在 (b)图中，构件以横向支撑处为分界点，上下节间变形形成两个半波，屈曲时整体呈“S”型，构件上没有出现“弯折”的情况。

图6 构件典型屈曲模式

2 计算模型

根据构件试验结果，假定屈曲模式为上述典型状态I和典型状态II，计算模型为单节间，以此为基础分别计算双角钢十字截面构件的弯扭屈曲荷载。

文献 ［14］推导了考虑弯曲屈曲和扭转屈曲的薄壁构件总势能公式。总势能在本文中可简化为:

式中:EIx，EIy，EIw，GIt分别为抗弯刚度、翘曲刚度、自由扭转刚度;Rc为截面对剪心的回转半径。

由构件几何边界条件假定形函数为:

由此对总势能Π积分，并令:

得积分后的总势能:

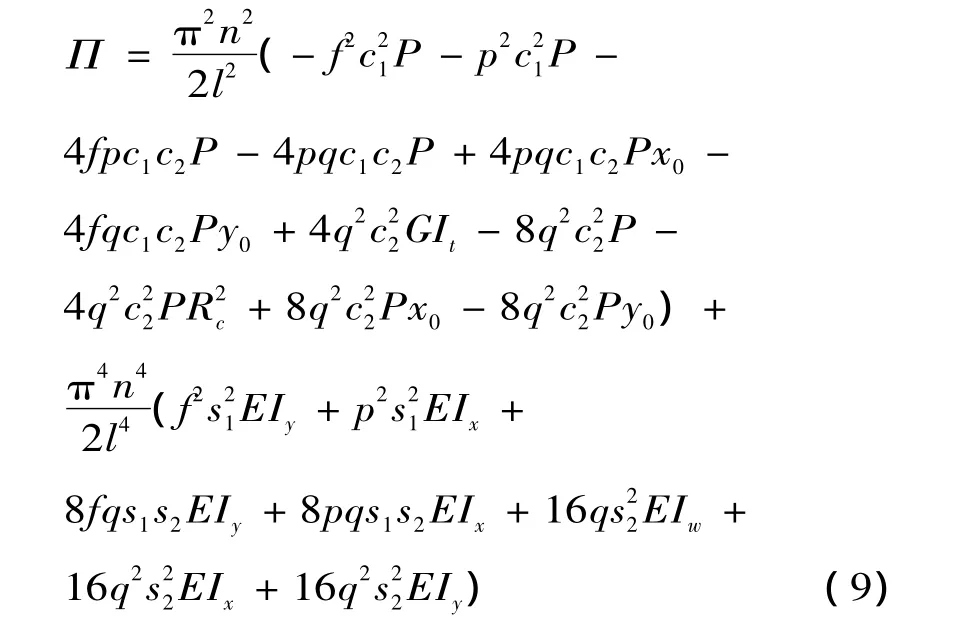
根据势能驻值原理对广义位移求一阶变分:

即可由里茨法求得弯扭屈曲临界荷载。对于非弹性弯扭屈曲，还应考虑应力超过比例极限后截面模量的折减，需用τ=［15］乘里茨法所得临界荷载Pcr得到构件的弹塑性屈曲荷载。

图7为试验、按典型状态I和II计算的稳定系数，横坐标为无量纲长细比，纵坐标为稳定系数。试验值在长细比较小时略低是因为初始缺陷对小长度构件影响较明显;由于构件两端靴板的有利作用没有计入理论模型，理论值整体略低于试验值;典型状态I下构件承载力低于典型状态II，与试验结果相符。

图7 稳定系数对比

3 建议的计算方法

现有设计方法［8］对十字截面构件的承载力折减主要从弯扭屈曲考虑，以弹性理论得到其弯曲屈曲荷载σx和扭转屈曲荷载σw:

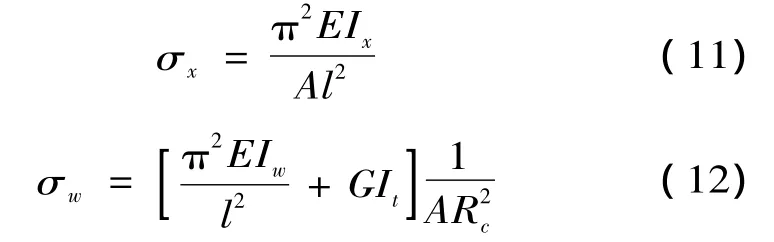
根据等稳定原则σx=σw，得到扭转屈曲换算长细比λz来考虑扭转的影响:

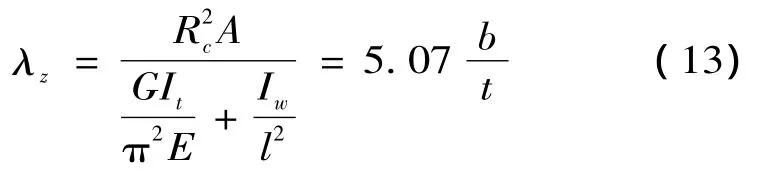
而试验表明，对双角钢十字截面构件扭转变形不明显，弯曲屈曲是主要的破坏形式。

同时，双角钢构件可简化为加载端均匀受压，另两边为简支、自由的板，此时其局部稳定临界应力为:

式中:v为材料泊松比。

为方便比较，可将 (12)式进一步整理为:

分析 (14)式和 (15)式可知，对十字截面σn=σw。这表明，扭转屈曲临界应力和局部稳定临界应力相同，只要构件满足局部稳定的要求即可不必考虑扭转屈曲，而局部稳定问题在规范中有单独计算方法。

因此从现有设计方法的理论基础和本次试验结果看，以扭转屈曲为出发点对十字截面构件承载力折减的方式不妥。

通过采用本文理论模型对L160，L200，L250等一系列不同壁厚的构件计算，对比两种屈曲方式下承载力差异，建议双角钢十字截面压杆承载力计算公式取如下形式:

式中:φ为轴心受压构件的稳定系数［8］;φw为双角钢构件轴心受压构件的稳定系数;N为轴压力;f为钢材强度设计值;A为构件毛截面面积。

如能确定构件不发生典型状态I的破坏，则可取

计算结果如图8所示。

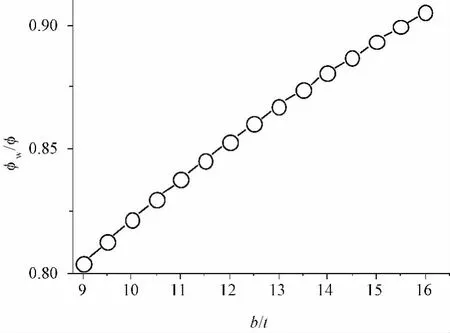
图8 承载力折减系数

4 结论

(1)双角钢十字截面构件整体变形以弯曲屈曲为主，由于两横向支撑的作用，使其弯曲变形有两种典型模式。当出现典型状态I时，构件计算长度不应按总长的一半考虑，这种效应在高强钢上体现的更明显。

(2)分析现有设计方法的理论基础和本次试验结果，发现其以扭转屈曲为出发点对十字截面构件承载力折减的方式不妥。

(3)通过计算模型分析两种典型状态下构件承载力差异，可知构件b/t对计算结果影响较明显，因此将其引入建议的计算公式。同时，如果通过构造措施能避免典型状态I出现，则不必考虑此种情况下承载力的折减。

［1］杨隆宇，李正良．考虑横向支撑刚度影响的组合截面压杆稳定承载力［J］．四川大学学报 (工程科学版)，2011，43(6):29－33．

［2］杨隆宇．特高压输电塔组合截面构件承载力理论与试验研究［D］．重庆:重庆大学，2011．

［3］韩军科，邱书清．输电铁塔十字组合双角钢构件稳定性规范对比 ［J］．建筑结构，2014，44(6):55－59．

［4］李正良，孙波，佘周，等．特高压输电塔双角钢组合截面构件的承载力 ［J］．重庆大学学报，2012，35(10):44－50．

［5］杨隆宇．考虑多种应力的组合截面填板承载力研究［J］．电力科学与工程，2014，30(8):33－37．

［6］高渊，韩军科，李清华．输电线路十字组合角钢主材拼接性能分析 ［J］．电力建设，2013，34(5):71－75．

［7］ Kalochairetis K E，Gantes C J．Numerical and analytical investigation of collapse loads of laced built-up columns ［J］．Computers and Structures，2011，89(12):1166 －1176．

［8］GB 50017－2003，钢结构设计规范 ［S］．

［9］DL/T 5154－2002，架空送电线路杆塔结构设计技术规定 ［S］．

［10］黄兰兰，李振宝，唐贞云，等．扭转屈曲对十字截面轴心压杆承载力的影响 ［J］．电力建设，2010，31(6):1－5．

［11］王智飞，苏京伟，张遨宇．输电铁塔十字组合角钢主材稳定承载力研究 ［J］．钢结构，2015，30(2):22－25．

［12］韩军科，邱书清．输电铁塔十字组合双角钢构件稳定性规范对比 ［J］．建筑结构，2014，44(6):55－59．

［13］ Trahair N S． Flexural-torsional buckling of structures［M］．The CRC Press，1993．

［14］童根树，张磊．薄壁构件弯扭失稳的一般理论 ［J］．建筑结构学报，2003，24(3):16－24．

On the Reduction Coefficient of Member Strength in Cross-like Section of High-strength Dual-angle Steel

Yang Longyu
(North China Power Engineering Co．，Ltd of China Power Engineering Consulting Group，Beijing 100120，China)

The design value for member strength in cross-like section of high-strength dual-angle steel does not match the tower’s full scale experiment．The majority of existing research concentrates on the description of test results，and in-depth analysis is insufficient．The widely used calculation model may lead to self-contradictory conclutions，which poses confusion for component design．In order to find out the causes of these differences，an experiment was conducted with L160×14，equal leg angle(λ=30－50)．A theoretical model was established based on the analysis of test results，with the influences of flex，warping，torsion considered．The equations were solved by energy principle，and two types of column curve under two typical buckling modes were obtained by Ritz method．The computation showed that the theoretical model with the overall and local stability considered was better at matching test results and the difference of bearing capacity under these two buckling modes was as much as more than 10%．By analyzing the deficiency of current design method，a formula was proposed in consideration of b/t．The proposed formula is the low range of test results，and can serve as a reference for engineering practices．

high-strength steel;cross-like section of dual-angle steel;bearing capacity;energy principle;reduction coefficient

TU392.6

A

10.3969/j.issn.1672-0792.2015.06.014

2015－04－03。

杨隆宇 (1981-)，男，博士，工程师，研究方向为输电线路杆塔设计、钢结构稳定，E-mail:yanglongyu@vip．163．com。