基于Hyperion的锡林郭勒草原光合植被、非光合植被覆盖度估算

李 涛, 李晓松, 李 飞

1 中国科学院遥感与数字地球研究所, 数字地球重点实验室, 北京 100094 2 中国科学院研究生院, 北京 100101

基于Hyperion的锡林郭勒草原光合植被、非光合植被覆盖度估算

李 涛1,2, 李晓松1,*, 李 飞1,2

1 中国科学院遥感与数字地球研究所, 数字地球重点实验室, 北京 100094 2 中国科学院研究生院, 北京 100101

掌握草原生态系统光合植被覆盖度(fPV)与非光合植被覆盖度(fNPV)时空动态对了解干旱半干旱草原生态系统特征(覆盖状况、火灾负载、载畜量、干扰及恢复等)及进行科学、有效地草地资源管理具有重要的意义。选取锡林郭勒典型草原为试验区，以Hypeiron高光谱数据为数据源，利用NDVI-CAI三元线性混合模型对试验区fPV和fNPV的时空动态分布进行了估算，并对不同端元选择方法(最小包含端元特征法、纯净象元指数法和实测法)对估算结果的影响进行了比较分析。研究结果表明，NDVI-CAI三元线性混合模型是同时估测锡林郭勒草原fPV和fNPV的有效方法，且估算的fPV和fNPV的季节变化与牧草的物候发育特征相吻合。不同端元选择方法对估算精度具有一定的影响，其中基于最小包含端元特征法提取端元进行估算的精度最高，fPV估算的均方根误差RMSE=4.57，估算精度EA=91.2%；fNPV估算的RMSE=5.90，EA=67.91%(样本数N=52)。

Hyperion; NDVI-CAI模型; 光合植被; 非光合植被; 端元选择

锡林郭勒草原是我国北方典型的温带干旱草原，面积达19.7万km2，可利用草原占90.6%，是内蒙古草原的主体部分；植被种类繁多，主要有大针茅、克氏针茅、羊草、蒿类等[1]。凭借着丰富的草地资源，锡林郭勒盟成为内蒙古重要的畜牧业生产基地，畜牧业产值占到农林牧渔总产值的65%左右[2]。然而近年来，超载放牧、毁草开地等人为活动及旱灾、雪灾等自然灾害造成草原大面积的破坏。草原退化、沙化及盐碱化现象日趋严重，草畜矛盾日趋尖锐，生态环境急剧恶化。光合植被(PV)和非光合植被(NPV)能够减缓径流，保持水土，影响土壤理化性质(渗透性，蒸发，孔隙，温度等)，改善土壤结构，增加土壤养分，提高土壤质量[3- 4]。光合植被覆盖度(fPV)及非光合植被覆盖度(fNPV)影响生态系统的碳储存、CO2交换量、植被生产力和地表能量平衡[5]，是衡量地表植被覆盖状况的重要参数，也是指示生态环境变化的重要指标。及时准确地估算fPV和fNPV能够反映牧草资源的空间分布及动态变化，可为制定正确的放牧管理政策、合理利用草原、保护生态环境提供科学依据。

fPV和fNPV的传统测算方法有目视估算法、采样法[6]和照相法[7]等地面实测方法。但这些方法实施繁杂，耗时耗力，不适合大面积、多频率的测算，而且易受主观性影响。遥感技术能够及时、客观、准确地估算大尺度的fPV和fNPV。目前对fPV的遥感研究较多，而对fNPV的研究很少。以往研究提出亮度指数BI、归一化指数NDI、归一化作物茬指数NDRI、土壤调整作物茬指数SACRI、木质素-纤维素吸收指数LCA等,能够较好地估算fNPV[8- 12]。但这些指数都基于仅有NPV与裸土(BS)两种成分，是否适用于PV、NPV和BS三者共存的情况有待研究。Daughtry等利用纤维素的吸收谷(2100 nm)和两吸收双肩(2021、2213 nm)3个波段的反射率，定义吸收深度为纤维素吸收指数(CAI)[13]。CAI与fNPV线性相关，基本不受土壤光学性质的影响[14- 15]，是估算fNPV的最佳指数；归一化植被指数(NDVI)可以区分PV与NPV和BS[16- 17]。基于此，Guerschman等[18]提出NDVI-CAI三元线性混合模型，采用纯净象元指数法确定端元特征值，较好地估算澳大利亚稀疏草原的fNPV和fPV的时空分布。然而该方法在其它区域的研究尚鲜有报道，其假设的合理及普适性以及端元选择的有效性都需要更多的应用与验证。

为此，本文以锡林郭勒草原为研究区，以高光谱Hyperion影像为数据源，尝试应用NDVI-CAI三元线性混合模型估算锡林郭勒草原的fPV和fNPV，并分析最小包含端元特征法、纯净象元指数法和实测法确定端元特征值的差异，对NDVI-CAI三元线性混合模型的结果进行精度评估，并在此基础上分析围封区自然草地fPV及fNPV的季节变化。

1 数据收集与预处理

1.1 研究区概况

研究区为内蒙古草原放牧控制实验区(116°39′E—116°41′E, 43°33′N—43°35′N)，位于内蒙古自治区锡林郭勒盟白音锡勒牧场境内。白音锡勒牧区平均海拔1100 m，是我国典型的温带草原区，属于大陆性半干旱草原气候。四季分明，春季多风，夏季暖湿，秋冬寒冷干燥。年平均气温-0.4 ℃，最冷月(1月)平均温度为-22.3 ℃，最热月(7月)平均温度达到18.8 ℃。光照资源比较丰富，全年光照为2603.8 h。年平均降雨量350 mm左右，80%集中于生长季6—9月份[19]。地带性土壤为栗钙土，有机质含量通常在1.5%—2.5%间，土层深度在1 m左右，腐殖层厚20—30 cm。植被以蒙古草原植被区系成分占优势，主要建群种与优势种为大针茅、克氏针茅、羊草和蒿类(变蒿和冷蒿)等[1]。

1.2 野外观测数据

为了评价模型估算精度，2012年8月2—8日对内蒙古草原放牧控制实验区内的56个样地进行观测。样地平均大小约90 m×180 m，对应Hyperion影像中3×6个像元，利用ArcGIS10.0中区域分析取样地对应像元的均值来代表该样地。根据每个样地的异质性特征选取3—6个1 m×1 m样方(图1)，采用鱼眼相机D90于样方正上方1.5 m处垂直拍摄3—5张照片。应用CAN_EYE_V636软件对鱼眼照片进行水平校正并人机交互式地监督分类，计算出各个样方的fPV和fNPV(图1)。取样地内所有样方的均值来代表该样地。另外，选择晴朗无云、风力较小、太阳光强度充足并稳定的时段(10:00—14:00)，将地物光谱仪(SVC HR- 768)的探头(视场角25 °)置于地物上方1 m处垂直向下，采集PV、NPV和BS三种端元的光谱(图1)，用于实测法确定端元特征指数值。

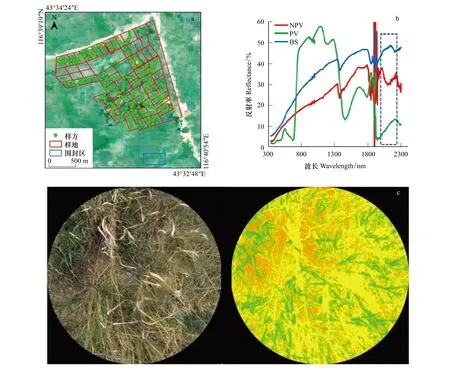
图1 研究区与地面数据采集

1.3 遥感数据及预处理

Hyperion传感器搭载于美国国家宇航局(NASA)2000年11月发射的地球观测卫星(EO- 1)，是第一个星载高光谱仪器，以推扫方式获取可见光/近红外和短波红外区域(356—2577 nm)的平均10 nm采样间隔的连续波谱数据，共242个波段，辐射分辨率16 bit，空间分辨率30 m[20]。Hyperion主要有Level0和Level1两级产品，其中Level1又分为L1A、L1B和L1R 3种。本文根据牧草的物候发育特征，从http://glovis.usgs.gov网站获取2012年的4.3、5.20、7.27、8.30和11.14五期Hyperion-L1R影像。

首先利用ENVI4.8去除未标定和受水汽影响的波段，剩下174个波段(8—57，79—120，128—165，180—223)；然后利用基于ENVI的Hyperion_Workshop模块进行坏线修复、去条纹、去smile效应；利用ENVI4.8的flaash模块进行大气校正，以精较准的TM影像为参考对Hyperion影像进行几何校正(精度在半个像元之内)[20]。最后用阈值对影像中的云和阴影地区掩膜处理。

2 研究方法

2.1 NDVI-CAI三元线性混合模型

图2 NDVI-CAI三元线性混合模型

NDVI-CAI三元线性混合模型假定像元由NPV、PV和BS三个成分组成，其NDVI和CAI指数符合线性关系(公式(1)—(5))，而且端元的NDVI和CAI指数不随时间变化[18]。影像的NDVI-CAI特征空间会表现为三角形(图2)。NPV的NDVI低、CAI高，位于三角形的左上角；PV的NDVI高、CAI几乎接近0，位于三角形的右侧中部；BS的NDVI、CAI均很低，位于三角形的左下角。

NDVI=(ρNIR-ρR)/(ρNIR+ρR)

(1)

CAI=[0.5×(ρ2.0+ρ2.2)-ρ2.1]×10

(2)

式中，ρNIR、ρR、ρ2.0、ρ2.1和ρ2.2分别为近红外、红波段、2000 nm、2100 nm和2200 nm处的反射率，计算时分别取671—691 nm、793—813 nm、2022—2032 nm、2102—2123 nm和2193—2213 nm波段反射率的平均值。此处CAI扩大了10倍，与NDVI均处在[-1,1]数量级上，便于绘制NDVI-CAI特征空间图。

V=∑fiVi=fPVVPV+fNPVVNPV+fBSVBS

(3)

C=∑fiCi=fPVCPV+fNPVCNPV+fBSCBS

(4)

∑fi=fPV+fNPV+fBS=100

(5)

式中，V代表NDVI，C代表CAI，f为百分比(%)。

采用公式(3)—(5)对Hyperion影像进行分解，分布在三角形内部的像元各成分比例均在0—100内，而对于分布在三角形外部的像元会出现大于100或小于0的异常值，采用公式(6)—(10)进行处理。最终获得研究区的fNPV和fPV估算值。

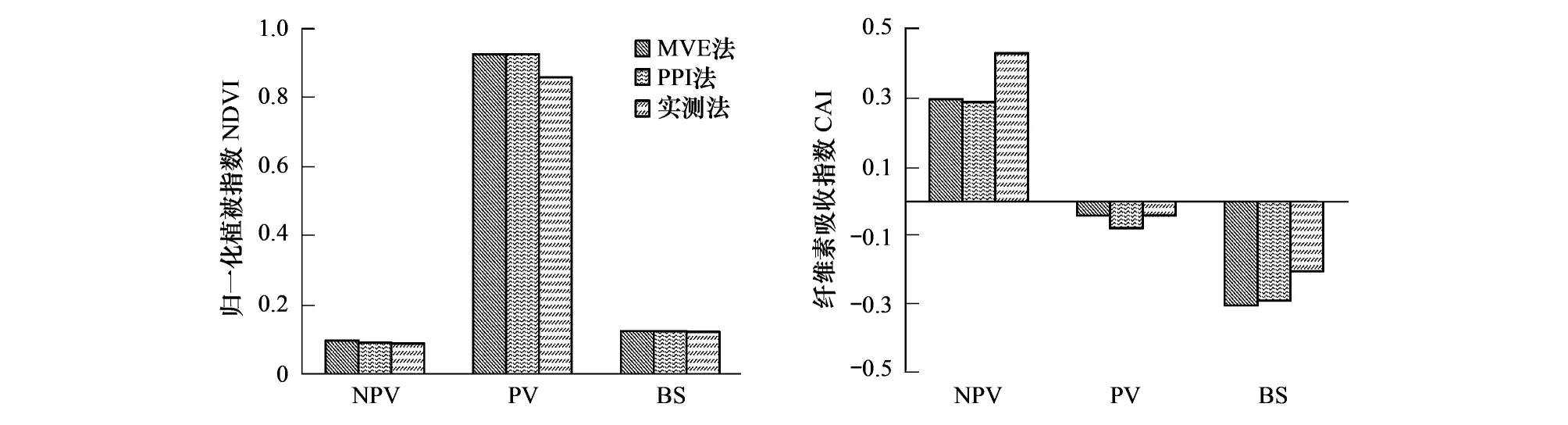
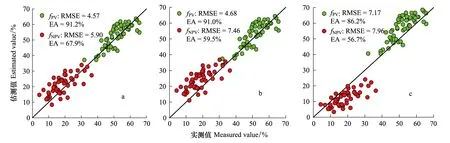
Cx=100，Cy=Cz=0 (100

(6)

Cx=0 (-20≤Cx<0)

(7)

Cy=Cy/(Cy+Cz)×100 (-20≤Cx<0)

(8)

Cz=Cz/(Cy+Cz)×100 (-20≤Cx<0)

(9)

Cx=Cy=Cz=0 (Cx>120或Cx<-20)

(10)

式中，Cx为混合像元分解后覆盖度落在[0,100]之外的端元类型，Cy和Cz为另外两种端元类型。公式10处理目的是将异常像元标记为无效值。

2.2 NPV、PV和BS端元特征值的确定

应用公式(1)—(2)计算五期Hyperion影像的NDVI和CAI指数，绘制NDVI-CAI特征空间图。理论上特征空间表现为三角形，利用PPI指数(PPI>10)来检验三角形顶点处是否存在纯净像元。若存在则说明三角形顶点可以作为纯净端元。

最小包含端元特征法(Minimum-Volume Enclosing method，MVE)：由于噪声的影响，影像的NDVI-CAI特征空间图可能不会呈现理想的几何图形。因此采用统计的方法，计算最小包含几何顶点区域像元的平均指数值作为相应端元的特征值。

纯净象元指数法(Pixel Purity Index method，简称PPI)：首先对Hyperion影像进行MNF变换，取变换后的前20个波段。设定迭代次数为2000，阈值系数为3，产生像元纯度指数PPI。将PPI>10且又靠近特征空间图顶点的像元视为纯净端元，取各个顶点纯净端元的平均指数值作为相应端元的特征值。

实测法：通过实地观测PV、NPV和BS三个端元的光谱曲线(图1)，来确定端元的特征值。

2.3 精度检验

本文采用均方根误差RMSE和估算精度EA来评价模型估算精度。

(11)

(12)

3 结果分析

3.1 端元特征值的确定

图3 五期Hyperion的NDVI-CAI特征空间图

五期Hyperion影像的NDVI-CAI特征空间(图3)表现为三角形。采用PPI指数验证，三角形顶点可以作为纯净端元。然后分别利用最小包含端元特征法、纯净象元指数法和实测法确定各个端元的特征值(图4)。三种方法确定的端元NDVI比较相近，最小包含端元特征法和纯净象元指数法确定的PV端元NDVI略高于实测法；而CAI差异较大，实测法确定的NPV和BS端元CAI明显大于最小包含端元特征法和纯净象元指数法，纯净象元指数法确定的PV端元CAI值小于最小包含端元特征法和实测法。

图4 三种端元提取法确定的端元特征值

3.2 估算精度检验

根据最小包含端元特征法、纯净象元指数法和实测法确定各个端元的特征值，利用NDVI-CAI三元线性混合模型对7月27日的Hyperion影像进行分解，估算出fPV和fNPV。采用52个样地(4个样地受云和阴影的影响严重，作为无效值区)的实测数据进行精度评价。绘制样地fPV和fNPV的实测值与估算值散点图(图5)。对于fPV，基于最小包含端元特征法和纯净象元指数法估算精度较高，散点基本都分布在参考线Y=X周围，均方根误差RMSE小于5，估算精度EA高达91%；而基于实测法明显高估，散点基本都落在参考线左上方，RMSE=7.17，相对较大，EA=86.2%，低于前两个方法。对于fNPV，基于最小包含端元特征法的估算效果最好，均方根误差RMSE=5.9，估算精度EA=67.9%，但也存在一定程度的高估；基于纯净象元指数法明显高估，散点基本位于参考线左上方；而基于实测法明显低估，散点基本位于参考线右下方，均方根误差最大，RMSE=7.96，估算精度最低，EA=56.7%。

3.3fPV和fNPV的季节性变化

基于NDVI-CAI三元线性混合模型，利用最小包含端元特征法确定的端元值，估算五期Hyperion影像的fPV和fNPV，并绘制fPV、fNPV和fBS的RGB合成图)。选择研究区内受人为及牲畜影响很小的自然草地(图6中蓝色框内)为感兴趣区，分析fPV和fNPV的季节变化(图7)。模型估算的fPV和fNPV的季节变化与牧草的物候发育特征吻合。感兴趣区4月初基本呈现荒芜状态，遗留着上一年的干枯植被，基本没有绿色植被，NDVI较低，CAI较高，fNPV高达95%，fPV约等于0；4月中旬以后，牧草开始返青，返青20 d后进入积极生长期，NDVI增加，CAI减小；5月20日时，fPV初步增加，fNPV减小(b)；7月中旬左右达到最大强度的生长；7月27日时牧草比较茂盛，大部分NPV已经被微生物分解，NDVI较高，CAI较低，fPV明显大于fNPV(c)；8月份陆续进入成熟期；8月30日时，fPV增加到68%，fNPV稍微减小；9月份陆续进入黄枯期，NDVI减小，CAI增加；到11月15日时，牧草已经枯黄，恢复到荒芜状态，fNPV高达95%，fPV约等0。

4 讨论

4.1 PV、NPV覆盖度估算的复杂性

光学遥感适用于估算彼此分离的PV和NPV覆盖度。而实际上，PV与NPV错综复杂，相互重叠，影响着表层植被的NDVI和CAI特征值，进而影响fPV和fNPV的估算精度。牧草生长初期，绿叶容易夹杂在上一年干枯牧草下，提高像元的NDVI而降低CAI，导致模型低估fNPV，高估fPV；而当牧草逐渐枯黄时，枯枝落叶容易夹杂在绿叶下，提高像元的CAI而降低NDVI，导致模型低估fPV，高估fNPV。相互交错的PV和NPV混合像元增加了NDVI和CAI的多变性，使得fPV和fNPV的估算变得复杂。

图5 fPV、fNPV估算精度分析图

图6 fPV、fNPV和fBS的RGB合成图

图7 感兴趣区fPV和fNPV变化图 (以均值代表整个感兴趣区)

牧草在衰败的过程中，叶片中水分和叶绿素减少，光谱特征逐渐转向以纤维素、木质素作用为主，NDVI值逐渐减小，CAI值逐渐增大。但此过程叶片中水分、叶绿素和纤维素三者共存，共同决定着叶片的NDVI与CAI。NDVI与叶绿素含量正相关；CAI与纤维素含量正相关；叶片中的水分吸收作用会降低CAI波段的反射率，减小纤维素的吸收深度，CAI值减小。叶片中水分、纤维素、叶绿素的含量变化过程及对叶片的NDVI和CAI的影响程度极其复杂，加大了fPV和fNPV的估算难度。

卫星传感器的倾斜角度和地形起伏共同决定着观测角度。不同观测角度对应像元不同的采样面积误差和地物的BRDF效应影响像元的NDVI和CAI，进而影响模型对fPV和fNPV的估算，即使在2种平坦的朗伯地物交界处影响依然很大[21]。这样对于一个混合像元，同时考虑BRDF效应和采样面积误差，像元的NDVI和CAI指数随观测角度的变化是增大还是减小不一定，这主要取决于混合像元内部各部分在不同角度的面积比和地物类型。角度效应增加了fPV和fNPV估算的复杂性。

4.2 NDVI-CAI三元线性混合模型的不确定性

线性光谱混合模型所用端元有限，简化了电磁波与地物复杂的相互作用过程，忽略了混合像元中其他成分的作用，势必造成估算误差，而且光谱分解结果容易受到影像质量的影响。另外端元的光谱异质性也是估算误差的重要来源[22]。NDVI-CAI三元线性混合模型利用多个波段计算出的指数，减小了端元不足、端元光谱异质性、以及影像质量等引起的误差，有助于fPV和fNPV的估算。

纯净端元的提取对模型估算精度起着至关重要的作用。最小包含端元特征法选取纯净端元，既能反映端元的平均光谱特征，又与遥感数据不存在尺度差异，减弱了端元光谱异质性的影响，提高整体的估算精度。但最小包含端元特征法在选择最靠近特征空间图顶点的像元时存在主观性和随机性，在一定程度上影响端元特征值的确定。利用纯净象元指数法确定端元，地物端元的光谱特征值往往是个极值，而且存在光谱异质性问题，不足以代表端元光谱特征，尤其端元的纯净像元较少时，容易产生较大误差。最小包含端元特征法和纯净象元指数法都基于存在纯净像元的前提，实际中纯净像元比较少，尤其是大尺度上。实测法不依赖影像，通过实地观测小尺度上纯净端元的光谱特征来作为像元尺度上的端元特征，势必带来尺度的问题。而且实地观测光谱与卫星成像时的条件(大气状况，观测角度等)不同，必然引入一些误差。

NDVI-CAI三元线性混合模型基于混合像元的NDVI和CAI指数符合线性这一前提。目前研究证实NDVI与fPV成线性关系[23- 24]，CAI与fNPV成线性关系[5]。但CAI指数容易受到其他因素的影响。BS的含水量和土壤成分影响其CAI，NPV的类型、分解程度、含水量影响其CAI[5]。在土壤质地、植被类型比较均一的地区，含水量成为影响估算精度的主要因素。在干燥至中等湿润条件下，PV、NPV和BS三者的CAI差异范围大，能够很好的分离，但随着含水量的进一步增加，三者的CAI差异逐渐减小，fPV和fNPV的估算误差增大[4]。因此，NDVI-CAI的三元线性混合模型适用于土壤质地和植被类型较均一的干旱半干旱地区，减小土壤类型、土壤成分、NPV类型等的影响。另外，绿色植被中的水分也会消弱减小CAI。fPV较小时对模型估算基本没影响，但随着fPV的增加(fPV>30%)，fNPV可能会低估[12,14]。本研究中绿色植被高覆盖，对于估算精度的影响需要进一步研究。

4.3 NDVI-CAI三元线性混合模型应用问题

NDVI-CAI三元线性混合模型中的CAI指数仅能从高光谱传感器中获取，如Hyperion。Hyperion已经超期运行，存在扫描条带和噪声问题，扫描宽度很窄[25]，回访周期较长，可获取的数据非常有限。并且单期Hyperion影像存在PV、NPV和BS三个纯净端元的机率很小。为了保证能从影像中选取PV、NPV和BS三个纯净端元，需要多期Hyperion影像，并且基于端元的NDVI和CAI特征值不随时间变化的假设。NDVI-CAI三元线性混合模型的应用受到Hyperion影像获取量的限制，还受到数据质量的影响，需要应用到多光谱传感器中，充分利用多光谱数据充足、覆盖范围大的优势。

Guerschman等[18]应用SR76(SR76=MODIS7/MODIS6)替代模型中的CAI指数，比较准确地估算了澳大利亚的无树大草原地区的fPV和fNPV，充分发挥MODIS高时间分辨率的优势。但是MODIS空间分辨率太低，空间异质性明显，端元提取比较困难。因此在MODIS影像中应用该模型需要检验其适用性。另外，BI、NDI、NDRI、SACRI、LCA等指数能够较好地估算fNPV[8- 12]，可尝试着将这些指数替代CAI，应用到NDVI-CAI三元线性混合模型估算fPV、fNPV。NDVI-CAI三元线性混合模型在多光谱遥感中有着深远的研究前景。

5 结论

本文基于NDVI-CAI三元线性混合模型，估算了锡林郭勒草原的fPV和fNPV，主要得到以下结论：

(1)NDVI-CAI三元线性混合模型是同时估测锡林郭勒草原fPV和fNPV的有效方法，锡林郭勒草地NDVI-CAI特征空间呈三角形分布，三个顶点分别代表PV、NPV与BS，满足三元线性混合模型的基本假设。

(2)不同端元选择方法对估算精度具有一定的影响，其中基于最小包含端元特征法提取端元进行估算的精度最高，fPV估算均方根误差为4.57，估算精度为91.2%；fNPV估算均方根误差为5.90，估算精度为67.91%(样本数N=52)。纯净象元指数法估算精度次之(fPV估算精度为91.0%；fNPV估算精度为67.91%)， 基于实测光谱端元估测精度相对最差(fPV估算精度为86.2%；fNPV估算精度为56.7%)。总体来说，PV的估测精度高于NPV, 基于实测光谱端元估测的精度要低于影像端元。

(3)基于NDVI-CAI三元线性混合模型估算的fPV和fNPV的季节变化与牧草的物候发育特征相吻合，可应用于分析锡林郭勒草原fPV和fNPV的时间变化。

[1] 朱敬芳, 邢白灵, 居为民, 朱高龙, 柳艺博. 内蒙古草原植被覆盖度遥感估算. 植物生态学报, 2011, 35(6): 615- 622.

[2] 魏利平. 不同因素对锡林郭勒盟草原退化影响程度研究 [D]. 内蒙古: 内蒙古农业大学, 2007.

[3] Arsenault E, Bonn F. Evaluation of soil erosion protective cover by crop residues using vegetation indices and spectral mixture analysis of multispectral and hyperspectral data. Catena, 2005, 62(2/3): 157- 172.

[4] Daughtry C S T. Discriminating crop residues from soil by shortwave infrared reflectance. Agronomy Journal, 2001, 93(1): 125- 131.

[5] Nagler P L, Inoue Y, Glenn E P, Russ A L, Daughtry C S T. Cellulose absorption index (CAI) to quantify mixed soil-plant litter scenes. Remote Sensing of Environment, 2003, 87(2/3): 310- 325.

[6] Morrison J E, Lemunyon J, Bogush H C. Sources of variation and performance of nine devices when measuring percent residue cover. Transaction of American Society of Agricultural Engineers, 1995, 38(2): 521- 529.

[7] BannariA, PachecoA, Staenz K, McNairn H, Omari K. Estimating and mapping crop residues cover on agricultural lands using hyperspectral and IKONOS data. Remote Sensing of Environment, 2006, 104(4): 447- 459.

[8] Major D J, Larney F L, Lindwall C W. Spectral reflectance characteristics of wheat residue // Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS′90). New Jersey: IEEE, 1990: 603- 607.

[9] McNairn H, Protz R. Mapping corn residue cover on agricultural fields in Oxford County, Ontario, using Thematic Mapper. Canadian Journal of Remote Sensing, 1993, 19(2): 152- 159.

[10] Biard F, Bannari A, Bonn F. SACRI (Soil Adjusted Corn Residue Index): un indice utilisant le proche et le moyen infrarouge pour la détection des résidus de culture de maïs. Proceedings of the 17th Canadian Symposium on Remote Sensing, 1995: 413- 419.

[11] Gelder B K, Kaleita A L, Cruse R M. Estimating mean field residue cover on Midwestern soils using satellite imagery. Agronomy Journal, 2009, 101(3): 635- 643.

[12] Daughtry C S T, Hunt E R, Doraiswamy P C, McMurtrey J E. Remote sensing the spatial distribution of crop residues. Agronomy Journal, 2005, 97(3): 864- 871.

[13] Daughtry C S T, Nagler P L, Kim M S, McMurtrey J E III, Chappelle E W. Spectral reflectance of soils and crop residues // Davies A M C, Williams P, eds. Near Infrared Spectroscopy: The Future Waves. Chichester, UK: NIR Publications, 1996: 505- 511.

[14] Daughtry C S T, Hunt Jr E R, McMurtrey J E. Assessing crop residues cover using shortwave infrared reflectance. Remote Sensing of Environment, 2004, 90(1): 126- 143.

[15] Bannari A, Chevrier M, Staenz K, McNairn H. Potential of hyperspectral indices for estimating crop residue cover. Revue Télédétection, 2007, 7: 447- 463.

[16] Daughtry C S T, McMurtrey J E III, Chappelle E W, Hunter W J, Steiner J L. Measuring crop residue cover using remote sensing techniques. Theoretical and Applied Climatology, 1996, 54(1/2): 17- 26.

[17] Wiegand C L, RichardsonA J. Relating spectral observations of the agricultural landscape to crop yield. Food Structure, 1992, 11(3): 249- 258.

[18] Guerschman J P, Hill M J, Renzullo L J, Barrett D J, Marks A S, Botha E J. Estimating fractional cover of photosynthetic vegetation, non-photosynthetic vegetation and bare soil in the Australian tropical savanna region upscaling the EO- 1Hyperion and MODIS sensors. Remote Sensing of Environment, 2009, 113(5): 928- 945.

[19] http: //www1. imau. edu. cn/shenggong/newx. php?type=18&id=246.

[20] Datt B, Jupp D. Hyperion Data Processing Workshop: Hands-on processing instructions, 2004.

[21] 郭占军, 阎广建, 冯雪, 王远征, 张霄羽. 遥感估算植被覆盖度的角度效应分析. 北京师范大学学报: 自然科学版, 2007, 43(3): 343- 349.

[22] Bateson C A, Asner G P, Wessman C A. Endmember bundles: A new approach to incorporating endmember variability into spectral mixture analysis. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(2): 1083- 1094.

[23] Wittich K P, Hansing O. Area-averaged vegetative cover fraction estimated from satellite data. International Journal of Biometeorology, 1995, 38(4): 209- 215.

[24] Purevdorj T S, Tateishi R, Ishiyama T, Honda Y. Relationships between percent vegetation cover and vegetation indices. International Journal of Remote Sensing, 2013, 19(18): 3519- 3535.

[25] Serbin G, Hunt E R, Daughtry C S T, McCarty G W, Doraiswamy P C. An improved SATER index for remote sensing of crop residue. Remote Sensing, 2009, 1(4): 971- 991.

Estimating fractional cover of photosynthetic vegetation and non-photosynthetic vegetation in the Xilingol steppe region with EO- 1 hyperion data

LI Tao1,2, LI Xiaosong1,*, LI Fei1,2

1KeyLaboratoryofDigitalEarthScience,InstituteofRemoteSensingandDigitalEarth,ChineseAcademyofSciences,Beijing100094,China2GraduateSchoolofChineseAcademyofSciences,Beijing100101,China

Quantitative estimation of the spatial and temporal dynamics of the fractional cover of photosynthetic vegetation (fPV) and non-photosynthetic vegetation (fNPV) in semi-arid grasslands is critical for understanding grassland conditions such as vegetation abundance, drought severity, fire fuel load, stocking rate, and disturbance events and recovery. It is also important for scientific grassland resource management. Over the past several decades, remote sensing has become an important tool for estimating the fractional cover of vegetation, which is a key descriptor of ecosystem function. However, most efforts have been devoted to the estimation offPVrather thanfNPV, although the latter is equally important, especially in arid and semi-arid ecosystems. This study describes a linear unmixing approach for estimatingfPVandfNPVin the Xilingol steppe region with hyperspectral and field investigation data. Five Hyperion images acquired on April 4, May 20, July 27, August 30, and November 15 in 2012 and a field-measured spectral library were utilized to explore the spectral feature space offPVandfNPVin order to validate the feasibility of a linear unmixing model. This model is based on two complementary spectral indices of vegetation that have been used in remote sensing analyses to discriminate green and dry vegetation from soils: the Normalized Difference Vegetation Index (NDVI) and the Cellulose Absorption Index (CAI). Different end-member extraction methods, including the Minimum-Volume Enclosing (MVE) method, the Pixel Purity Index (PPI) method, and a field measurement method, were adopted to retrieve the end-member values of photosynthetic vegetation, non-photosynthetic vegetation, and bare soil, respectively, from NDVI and CAI. Then, the influence of end-member extraction on the accuracy of thefPVandfNPVestimation was evaluated through comparison with field-measuredfPVandfNPVvalues acquired from classifications performed on fisheye photos (N=52). Subsequently, the optimum unmixing strategy was utilized to retrieve the temporal dynamics offPVandfNPVin a fenced area, where the grassland was not influenced by human activities, so that the usefulness of these fractional coverage indices could be validated by checking their consistency with the phenology of natural grassland. The result shows that the linear unmixing model based on NDVI and CAI was effective for estimatingfPVandfNPVin the Xilingol steppe region. The NDVI-CAI feature space follows a triangular distribution, where the three vertexes represent photosynthetic vegetation, non-photosynthetic vegetation, and bare soil, meeting the essential requirements of the linear unmixing model. The estimation accuracy was different for the different end-member extraction methods. The MVE-based estimation had the highest accuracy, with estimated accuracy of 91.2% and 67.91% forfPVandfNPV, respectively, followed by the PPI-based estimation (91.0% and 59.5% forfPVandfNPV, respectively) and the field-measurement-based estimation (86.2% and 56.7% forfPVandfNPV, respectively). In general, the estimation accuracy was higher forfPVthanfNPV, and the field-measured end-member performed worse than the image end-member, which was probably due to the inconsistency between the field-measured spec and the Hyperion spec. Additionally, the temporal dynamics offPVandfNPVwere confirmed to be consistent with the phenological seasonal change in natural grasslands. Therefore, the method proposed here can be used to monitor the temporal and spatial variations offPVandfNPVin semi-arid grasslands.

Hyperion; NDVI-CAI model; photosynthetic vegetation (PV); non-photosynthetic vegetation (NPV); end-member selection

国家科技支撑计划(2011BAH23B04); 国家科技重大专项(21-Y30B05- 9001- 13/15)

2013- 08- 14;

2014- 06- 12

10.5846/stxb201308142075

*通讯作者Corresponding author.E-mail: lixs@radi.ac.cn

李涛, 李晓松, 李飞.基于Hyperion的锡林郭勒草原光合植被、非光合植被覆盖度估算.生态学报,2015,35(11):3643- 3652.

Li T, Li X S, Li F.Estimating fractional cover of photosynthetic vegetation and non-photosynthetic vegetation in the Xilingol steppe region with EO- 1 hyperion data.Acta Ecologica Sinica,2015,35(11):3643- 3652.