一类具有退化平衡点的概周期微分方程的可约化性

邱汶华，孟凡卉

(枣庄学院数学与统计学院，山东枣庄277160)

一类具有退化平衡点的概周期微分方程的可约化性

邱汶华，孟凡卉

(枣庄学院数学与统计学院，山东枣庄277160)

本文主要研究一类概周期微分方程在退化平衡点附近的摄动问题.以KAM方法为工具，摄动系统可以通过一个概周期变换化成以零为平衡点的正规形.研究的概周期微分方程是变系数的.

概周期解;KAM方法;退化的平衡点①

0 引言

近年来，J.X.Xu和J.G.You研究了下面的概周期微分方程［1-3］:

找到了一个仿射的实解析拟周期变换，使得上述方程变换成以零为平衡点的系统，从而有拟周期解.作者［4，5］也先后研究了不同类型的微分方程的可约化性问题.

受上述工作的启发，本文我们研究下面的非线性概周期微分方程:

其中n是一整数，A是一正数，ε为小参数，h是高阶项，f是小摄动项.在一定的条件下，通过一个仿射的概周期变换，上述方程可约化为一个以零为平衡点的正规形.

1 相关的定义

定义1如果有一个连续函数，F(θ1，θ2，…，θr)，和实数ω1，ω2，…，ωr，，使得f(t)= F(ω1t，ω2t，…，ωrt)，则称函数f(t)是拟周期的，ω=(ω1，ω2，…，ωr)称为f的频率.如果f(t)=，其中fi(t)(i=1，2，…)均为拟周期的，则称f(t)为概周期的.

为了克服具有无穷多个频率的小分母带来的困难，需要一个较强的范数.为此引入有限空间结构的相关概念.

定义2设N是自然数集，τ是由N的子集组成的集合.称(τ，［.］)是N上的有限空间结构，如果τ满足:

(1)φ∈τ，(2)若Λ1，Λ2∈τ则Λ1∪Λ2∈τ，(3)=N，而［.］是定义在τ上的函数，满足［φ］=0，［Λ1∪Λ2］≤［Λ1］+［Λ2］，［.］称为τ上的权函数.

定义3设Q(t)=，对m＞0，ρ＞0，‖Q(t)‖m，ρ=称为Q(t)在有限空间结构(τ［.］)下的权范数.

2 主要定理及其证明

引理1考虑如下带有参数的实解析的概周期系统:

N+(p)=(A+ε［a］)ξ2n+1-λ+h+(p).方程(2)还满足下面的条件:

则对于任意的p∈M+，存在一个仿射实解析的概周期变换

Φ:x+∈D(0，r+)→x=eu(t，p)((1+εQ)x++v(t，p))∈D(0，r)，

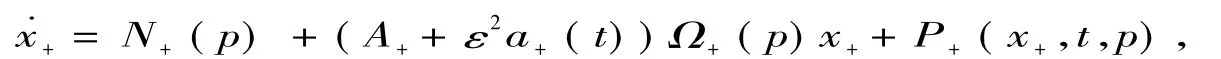
证明:引理的证明由经典的KAM方法来完成的.变换Φ由三个变换复合而成.

变换Φ1:x=eu(t，p)y，其中∂ωu=RK1-(A+εa(t))［R1］.通过变换Φ1原方程变为

变换Φ2:y=z+v，其中∂ωv-A+Ω+v=RK0-［R0］-N+u.通过变换Φ2方程变为

变换Φ3:z=(1+εQ)x+，其中(a(t)-［a］)Ω+(t)Ω+通过变换Φ3方程变为

因此，通过变换Φ=Φ1°Φ2°Φ3:x=eu((1+εQ)x++v)方程(2)变为

引理1得证.接下来介绍本文的主要结果.

定理2设方程(1)满足下述三个条件:

(1)函数a，h和f关于所有变量是实解析的，同时关于t是概周期的，其频率向量为～ω=(ω1，ω2，…)，它们具有有限空间结构(τ，［.］);

(3)h=O(x2n+2)(x→0)，当固定m0，s＞0时，有＜+∞.

则存在充分小的，使得当时，存在一个仿射的实解析概周期变换x=y+u(t)，原方程(1)变换成

其中f*(y，t)=O(y)(y→0).

证明:令x=ξ+y，|ξ|≤δ，|y|≤r0≤δ.则方程(1)变成

对(y+ξ)2n+1展开，整理后即为

其中P=ε~a(t))ξ2n+1+(A+εa(t))g+h+f.

接下来我们将要证明当ε充分小时，存在一个ξ*，使得当ξ=ξ*时，方程(4)约化为以零为平衡点的正规形.为此引入外参数，即

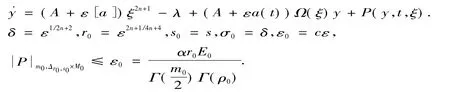
根据引理1，对方程进行无穷次迭代并收敛，变换x=Φ(y，t，p*)，则方程(4)变成

因此，通过变换x=Φ(y+ξ*，t，p*)，原方程(1)变成了方程(3).又Φ(y+ξ*，t，p*)=y+u*+ξ*，则有x=y+u(t)，u(t)=u*+ξ*，定理得证.

［1］V.I.Arnold，齐民友译.经典力学的数学方法(第四版)［M］.北京:高等教育出版社，2006.

［2］T.Kappeler，J.Poschel.Kdv方程和KAM理论(影印版)［M］.北京:高等教育出版社，2010.

［3］J.S.Geng，J.Wu.Real analytic quasi-periodic solutions for the derivative nonlinear Schrodinger equations［J］.J.Math.Phys.，2012，53:102702.

［4］Wenhua Qiu and Jianguo Si.Reducibility for a Class of Almost-Periodic Differential Equations with Degenerate Equilibrium Point under Small Almost-Periodic Perturbations［J］.Abstract and Applied Analysis，2013，12，386812:1-9.

［5］Wenhua Qiu and Jianguo Si.On small perturbation of four-dimensional quasi-periodic systems with degenerate equilibrium point［J］.Communications On Pure and Applied Analysis，2015，14(2):421-437.

［6］邱汶华.具有退化平衡点的微分方程的可约化性［D］.济南:山东大学数学学院，2014.

［7］张吉庆，李同荣.具有分布时滞神经网络系统的全局稳定性分析［J］.枣庄学院学报，2014，31(2):15-19.

［8］王宁宁，祝晓薇，张利群，等.一类平面二次系统(III)类方程的同宿分支问题［J］.枣庄学院学报，2013，30(2):23-27.

［责任编辑:闫昕］

Reducibility for a Class of Almost-Periodic Differential Equations with Degenerate Equilibrium Point

QIU Wen-hua，MENG Fan-hui
(School of Mathematics and Statistics，Zaozhuang University，Zaozhuang 277160，China)

This paper focuses on almost-periodic time-dependent perturbation of an almost periodic differential equation near degenerate equilibrium point.Using the KAM method，the perturbed equation can be reduced to a suitable normal form with zero as equilibrium point by an affine almost periodic transformation.The almost periodic differential equation have the variable coefficient.

almost periodic solution;KAM method;degenerate equilibrium point

O175.12

A

1004-7077(2015)02-0061-03

2015-01-23

枣庄学院博士科研基金项目(项目编号:2014BS05).

邱汶华(1980-)，男，山东滕州人，枣庄学院数学与统计学院讲师，博士，主要从事微分方程定性理论中KAM理论的研究.