由“圆的对称性”谈小组合作模式

朱胤

“小组合作学习”是一种新的学习方式，对促进学生间的情感交流、互帮互学、共同提高，发挥了积极的作用。教师在对学生开展小组合作学习时，一定要保证有效的合作，应关注每一个学生的进步和发展，让课堂教学变得轻松自如。

教学片段再现

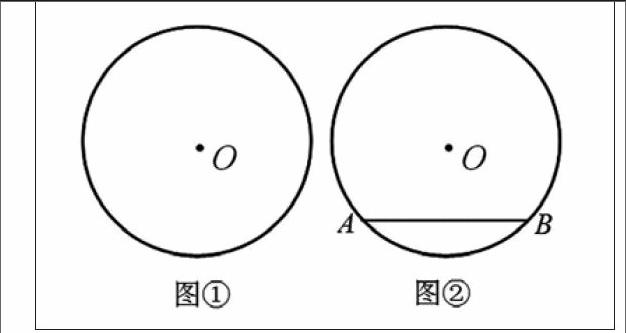
前置学习 问题一：在图①中画出⊙O的一条对称轴；与同伴交流一下，大家画的对称轴有什么特点？问题二：如图②，已知AB是任意一条弦，试在图②中画出这个图形的对称轴；交流一下你的画法，并尝试说说这样画的理由。

师：请大家在小组中交流、订正问题一和问题二，并请组长记录下本组的做法。

生1：问题一是圆的对称轴是直径所在的直线，易错点是不能漏了“所在直线”。圆的对称轴的特点是它们都经过圆心。

师：好。请大家交流问题二中的画法，上台展示。

生2：我们组有两种方法：一是作AB的垂线；二是以A、B为圆心，连接两圆的交点的连线。

师：这两种做法是否都正确？

生：不对。

师：如何修改？

生3：增加条件“以大于AB的长为半径”，就是画了AB的中垂线。

师：我们把第二种画法改为“画AB的中垂线”，这样更简洁明了。

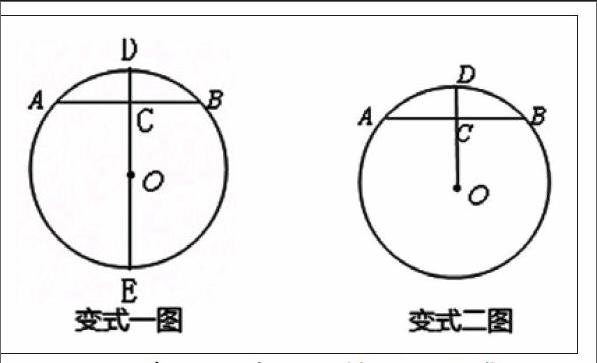
例练巩固 例题：已知在⊙O中，弦AB的长为8cm，圆心O到AB的距离OC为3cm，求圆O的半径。变式一：如图，在半径为5cm的⊙O中，有长8cm弦AB，求点O与AB的距离；在学生练习后，总结出一个直角三角形，三条边由“弦的一半，弦心距，半径”构成。变式二：试就右图，参考例题及变式一，编写一道题目，记下来。

师：请组长花1分钟时间收集好小组成员编写的问题，并交流。

生1：我们组编的题目有：①已知OC=4，OB=6，求AB的长；②已知AB=10，OB=6，求CD的长；③已知CD=2，AB=8，求圆的半径。

生2：我们组还编了：④已知弧AB的度数为60°，半径OB长为6，求弦AB长度。

生3：我们组还编了：⑤已知∠ABO的正切值为，半径OB长为10，求弦长AB、CD、弦心距OC。

师：编的都很好，特别是③④⑤几个问题，请大家课后去练习这些问题。

小组合作的几点思考

给予充分时间讨论，是进行有效合作学习的前提 小组合作学习时，要给学生充分的讨论时间，否则非但达不到合作学习的目的，而且很容易挫伤学生学习的热情，养成敷衍了事的不良习惯。因此，教师需给学生充分的时间，使每位学生在小组内充分表达自己的思路、想法，学会接受别人，欣赏别人，取长补短。笔者尝试发现，经过小组充分讨论解决的问题，往往学生理解得比较透彻，不容易遗忘，虽然在讨论时多花了两三分钟时间，但却有事半功倍的效果。

明确讨论时间，是进行有效合作学习的基础 任何事情如果没有时间作保证都将落入形式主义，合作学习也是如此。虽然教师要给学生充分讨论的时间，但也不能没有时间的限制。第一，经常性的无限时讨论，教师的教学内容肯定无法完成；第二，经常性的无限时讨论，必将使学生养成拖拉、懒散的习惯；第三，经常性的无限时讨论，容易让学生找到钻空子的机会，一些学习不自觉的学生就会在讨论时做一些与学习无关的事情，从而降低课堂效率。因此，笔者认为，在进行小组讨论时，一定要明确小组讨论的时间，否则就成了“低效”的合作学习。

设置开放问题，全员参与，是进行有效合作学习的途径 本节课中，教师设置了这样的一个问题：“试就右图，参考例题及变式一，编写一道题目，记下来。（数据不要过大）”这是本堂课的一个亮点，课堂上每一位同学都积极思考、交流讨论并与全班同学分享自己的成果。从学生自编的问题可以看出，这一开放性问题满足了学生的个性化需求，稍差的学生也能够掌握最基本的方法，编出一些基本题；思维能力强的学生能从不同角度去思考、理解，编出高质量的问题，如问题③④⑤，或利用方程解决问题或与前面知识结合，得到一道稍有综合的、新颖的题目。

小组合作的“组织性”，是进行有效合作学习的保障 本节课中，教师始终依托每个小组的组长开展教学。比如在变式一的处理中，由于问题比较简单，因此教师采用“批改组长答案——组长批改组员作业——组内相互订正”的方式，保证所有学生都能掌握基础知识。在变式二的处理中，由于问题有一定的难度，先让学生进行独立思考，再交流讨论，最后由组长收集汇报。从变式二的交流来看，学生提出了不同层次的问题，说明小组合作能集思广益，保证课堂教学有效开展。

（作者单位：江苏省太仓市第一中学）endprint