多维题组效应认知诊断模型

詹沛达 李晓敏 王文中 边玉芳 王立君

(1浙江师范大学心理系,金华 321004) (2北京师范大学认知神经科学与学习国家重点实验室,北京 100875)(3香港教育学院评估研究中心,香港)

1 引言

认知诊断评估(cognitive diagnostic assessment,CDA)不仅有助于人们更深入地了解隐藏在学生总分背后的认知结构、加工技能和认知过程之间的差异,还能提供该学生的认知诊断报告和补救性教学建议,对学生个体的发展起到了积极的促进作用。要对学生的内部心理加工过程进行测量、诊断和评估就需要认知诊断模型(cognitive diagnostic models,CDM)。常见的CDM有DINA模型(Haertel,1989;Junker &Sijtsma,2001)、DINO模型(Templin &Henson,2006)、LCDM (Henson,Templin,&Willse,2009)等。与此同时,在实际心理或教育测验中也经常出现多个项目共用相同刺激(stimulus)的情况(如：篇章阅读题型),这种受共同刺激影响和制约的项目集合通常被称为题组(testlet) (Wainer &Kiely,1987)。使用题组可以节约考生阅读材料的时间,提高测验的效率,提供逻辑关系更强的材料(DeMars,

2006;Wainer,Bradlow,&Wang,2007;Huang &Wang,2013;詹沛达,王文中,王立君,李晓敏,2014)。目前,如 TOEFL、GRE、PISA、PIRLS等大型测验均涉及了大量的题组,对题组进行研究的必要性日显重要。当测验存在题组时,由于嵌在题组内的项目共用相同的题组刺激,这时题组项目反应间就存在一定的相依性,即相依于题组效应。为了合理有效地处理题组效应,研究者们也开发出了一系列题组反应模型(testlet response models,TRM),如：Rasch题组模型(Wang &Wilson,2005)、广义题组模型(Li,Bolt,&Fu,2006)、高阶题组模型(Huang &Wang,2013)等。

Rupp和Templin (2007)曾指出当前认知诊断领域还缺少对包含题组的测验进行诊断分析的研究。可以说,目前CDM和TRM仍处于相互独立的开发阶段,即已开发的 CDM 无法有效处理含有题组效应的测验数据,且已开发的 TRM 不具有对被试知识结构或认知过程进行诊断的功能。因此,开发出一种既具有认知诊断功能的又能有效处理题组效应的项目反应模型仍是很有必要的且值得研究的。对此,本文把具有认知诊断功能的线性 Logistic模型(LLM) (Maris,1999)和多维题组效应Rasch模型(MTERM) (詹沛达等,2014)相结合,首先提出了一种假设认知属性间具有补偿作用的多维题组效应认知诊断模型(compensatory multidimensional testleteffect CDM,C-MTECDM),并在此基础上,提出了另一种假设认知属性间具有非补偿作用多维题组效应认知诊断模型(noncompensatory multidimensional testleteffect CDM,N-MTECDM),之后根据C-MTECDM、N-MTECDM和已有TRM的共同点,提出了更一般的 Logistic题组框架(Logistic testlet framework,LTF),以期找到一种可以有效解决该问题的方法。

2 多维题组效应认知诊断模型的开发

2.1 题组效应及多维题组效应模型简介

题组效应是指当被试对题组项目的反应依赖于被试对题组刺激的整体认知时,项目反应间存在的一种相依性。即题组效应是一种测验目标潜在特质(潜质)以外的影响项目反应的潜质(詹沛达,王文中,王立君,2013)。那么将题组效应引入CDA后,就可将其理解为一种测验目标属性(即Q矩阵所包含的属性)以外的影响项目反应的潜质。

詹沛达等(2014)将题组效应划分为项目内单维题组效应和项目内多维题组效应,如图1所示,进而提出了MTERM,其中二级评分的MTERM可描述为(log-odds,下同)：

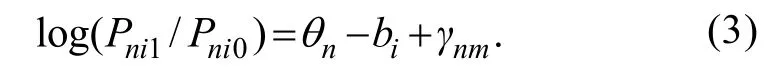
詹沛达等(2014)指出 MTERM 更具普适性,即便当作答数据不存在题组效应或只存在项目内单维题组效应,采用该模型簇进行测验分析也能得到较好的参数估计结果。因此,使用多维题组效应向量参数而不是单维题组效应参数可以提高新模型的适用范围。

图1 项目内单维/多维题组效应示意图。θ表示被试能力,γ表示题组效应,□表示项目

2.2 Q矩阵及LLM简介

CDM与Q矩阵(Tatsuoka,1985)是CDA的两个重要组成部分。首先,Q矩阵是连接项目与属性的纽带,通常Q矩阵(

I

×

K

,其中

I

表示项目数量,

K

表示属性数量)是由数值 0与 1所组成的,它的元素

q

界定了项目

i

与第

k

个属性间的关系,若

q

=1表示项目

i

考查了第

k

个属性,反之为

q

=0。另外,对比式(4)与式(2)后可发现,U矩阵与Q矩阵的功能类似,差异仅在于Q矩阵用于界定项目与属性之间的关系,而U矩阵用于界定项目与题组效应之间的关系。

式中,

P

1和

P

含义同上;

α

为被试

n

对第

k

个属性的掌握情况,有

α

∈ {0,1};

q

为项目 i对第

k

个属性的考查情况,有

q

∈ {0,1};

λ

为项目

i

的截距,exp (

λ

)/[1+exp (

λ

)]用于描述正确作答项目

i

的基线概率;

λ

为项目

i

中属性

k

的权重(即

λ

≥0),用于描述掌握属性

k

对正确作答项目

i

的概率的对数发生比的增量;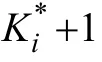

LLM是一种补偿(compensatory)模型,其假设被试掌握任一项目所考查的属性均会增加其正确作答的概率,且这种贡献与掌握其他属性所产生的贡献相独立。

2.3 多维题组效应认知诊断模型

2.3.1 补偿型多维题组效应认知诊断模型

为解决在 CDA中实现对含有题组效应的数据的有效处理,本文首先将MTERM和LLM相结合,提出一种假设各认知属性对正确作答概率(的对数发生比)有补偿作用的 CDM,其项目反应函数可描述为：

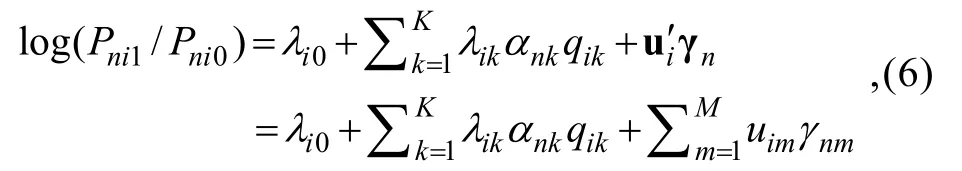
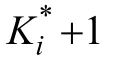
2.3.2 非补偿型多维题组效应认知诊断模型

在CDM中,除了补偿模型外还有一类较为常见的非补偿模型,如：DINA模型、NIDA模型等。通常在非补偿模型中,当且仅当被试掌握项目所考查的全部目标属性时才有较高的正确作答概率。此时,可将 C-MTECDM 中用于描述属性的“连加模块”改变为“连乘模块”,则有：

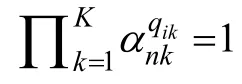
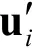
进而有：

除对属性掌握模式与项目反应关系间的描述存在差异外,N-MTECDM仍保持与C-MTECDM一致的特性：(1)采用logit联接函数;(2)假设题组效应为连续潜质;(3)各题组效应间满足正交结构。

2.4 Logistic题组框架

上文共提出了两种具有认知诊断功能的题组模型,它们之间的差异在于对属性掌握模式与项目反应关系间的描述不同。其实,在观察 MTERM、Rasch题组模型、C-MTECDM、N-MTECDM以及双参数题组模型(Bradlow,Wainer,&Wang,1999)和高阶题组模型(Huang &Wang,2013)等后可发现,它们之间的主要差异也仅在于对潜变量的描述方式不同,如图2。

图2 logit联接函数下各题组反应模型的联系与区别

即它们均可被视为由3个模块组成,则可将它们统一描述为：

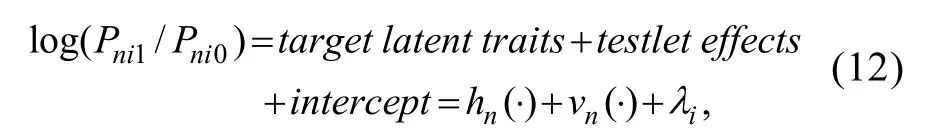
式(12)可被称为Logistic题组框架(LTF),其中,

模块 2 “

testlet effects

”或

v

(·)是 LTF 中用于描述项目反应中的题组效应(非目标潜质),目前包括较常见的项目内单维题组效应参数和更具普适性项目内多维题组效应向量参数。研究者也可根据实际情况对题组效应添加区分度参数。通常假设题组效应与目标潜在特质之间不存在交互作用(DeMars,2006;Wang &Wilson,2005;Huang &Wang,2013;詹沛达,2014),因此在LTF中模块1与模块2是求和(补偿)关系。模块 3 “

intercept

”或

λ

的含义与潜变量的类型有关。通常,当潜变量为连续变量时,

λ

用于描述项目特征曲线拐点所对应的横坐标,此时

λ

可被称为项目定位参数或难度参数;而当潜变量为类别变量时,exp (

λ

)/[1+exp (

λ

)]可用于描述正确作答项目

i

的基线概率,此时

λ

可被称为截距参数。

为探究 C-MTECDM和 N-MTECDM的性能,本文将包含2个研究,研究1的主要目的是对两个模型进行参数返真性检验,以期检验参数估计方法是否能够提供较好的参数估计结果;研究2中分别将C-MTECDM和N-MTECDM与忽略题组效应的CDM 进行了对比研究,以期向读者展示忽略题组效应对测验分析结果所带来的危害。

3 参数估计

本研究使用基于 MCMC算法的 WinBUGS(version 1.4,Spiegelhalter,Thomas,&Best,2003)进行参数估计,设定每种实验条件进行

R

=10次循环以期减小随机误差,这与其他一些使用 MCMC算法的研究类似(e.g.,Li et al.,2006;Huang &Wang,2013;詹沛达,2014),每次循环设定链数为 3,每条链中迭代5000次并预热(burn-in)前2000次迭代结果,取后 3000次迭代结果的平均数为该链的参数估计结果,最后取3条链的估计结果的平均值作为该循环的估计结果(各参数估计均收敛)。设定待估计参数的先验分布满足：

λ

～

U

(–3,3)、

λ

～

U

(0,5)、

λ

～

U

(0,5)、

α

～

Bernoulli

(0.5)、γ～

MVN

(0,Σ)。根据条件独立假设或广义局部独立假设(詹沛达等,2013)有联合后验分布为：

则各参数的满条件分布为：

进而,MCMC算法的抽样过程如下,

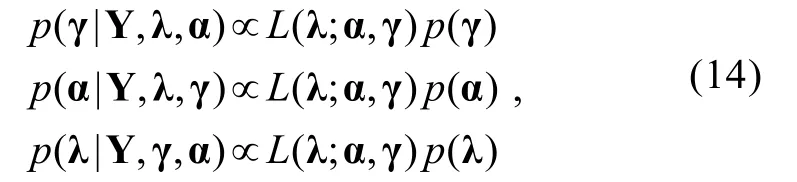
t

为迭代次数：(1) γ参数,γ从多元正态分布

MVN

(γ,Σ)中随机抽取,转移概率为：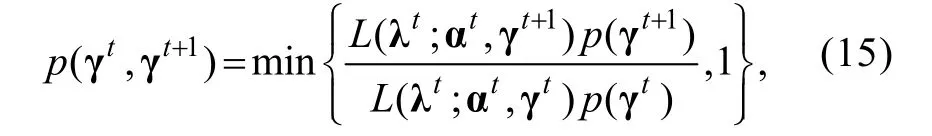

(2) Σ,多维题组效应协方差矩阵(Σ)从

M

维逆Wishart分布

W

[R,

M

]中直接抽取,R为

M

阶单位矩阵,(3) α 参数,

α

从建议分布

Bernoulli

(0.5)中随机抽取,转移概率为：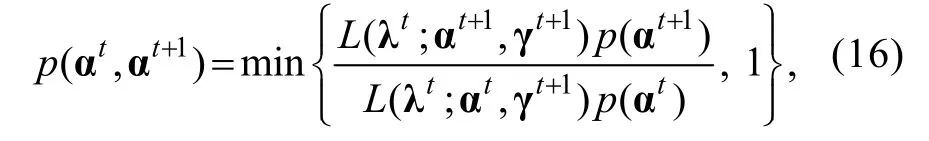

(4) λ参数,λ从建议分布

N

(λ,1),转移概率为：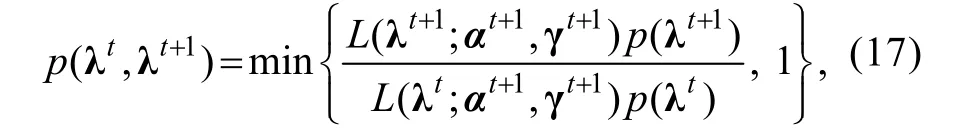

4 研究1

4.1 研究设计

4.1.1 Q矩阵与U矩阵的设定

本研究设定考查属性个数为

K

=4,题目数

I

=30,则Q矩阵见表1。并设定该模拟测验包含3个篇章阅读：第1篇包含第1题～第10题、第2篇包含第11题～第20题、第3篇包含第21题～第30题,且存在交叉分类结构(crossed classification structure,即项目反应受到项目内多维题组效应影响),则 U矩阵的设定同见表1。

4.1.2 项目参数、题组效应与被试属性掌握模式的设定

本研究采用R软件(version 3.0.2,http://www.rproject.org)自编程序来实现数据模拟。

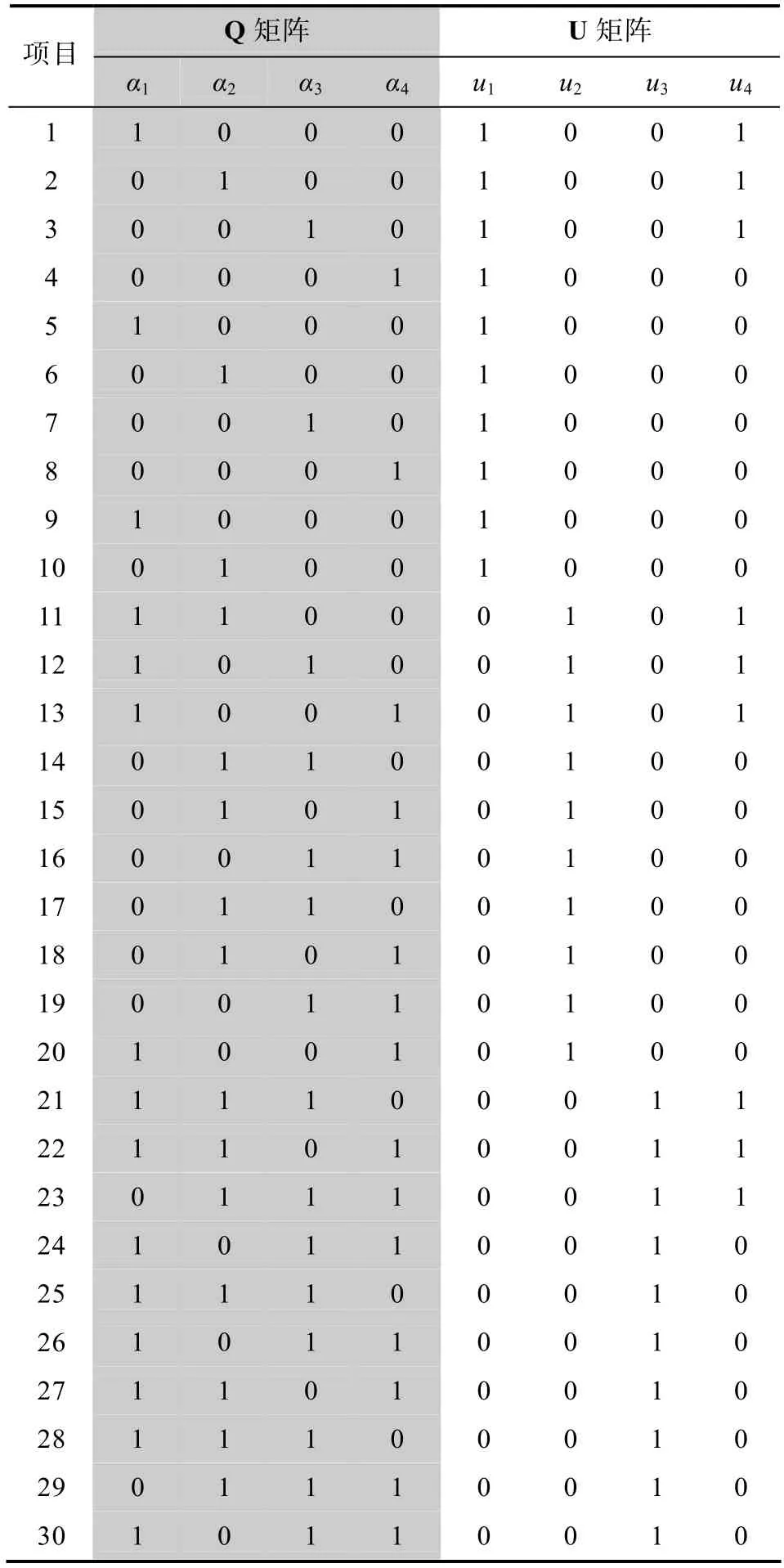
表1 Q矩阵与U矩阵

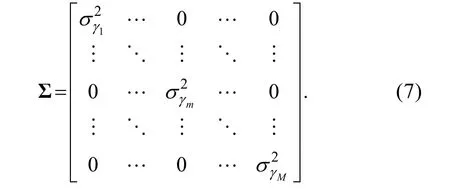
考虑到 MTECDM 的复杂性(同时包含潜在类别变量和潜在连续变量)和Q矩阵的设定(共包含8个维度潜变量),根据已有关于多维项目反应模型的研究(e.g.,Ackerman,1994;Yao &Boughton,2007)可推断出欲对MTECDM实现较精准参数估计很可能需要较大的样本量。因此设定 3个样本容量(1600、3200和4800)以期探究MTECDM的参数估计返真性,具体设定方法为：目标属性数

K

=4,即共有2=16种属性模式,设定每种属性模式人数分别为100、200和300人。4个题组效应满足多元正态分布

MVN

(0,Σ),其中对角阵：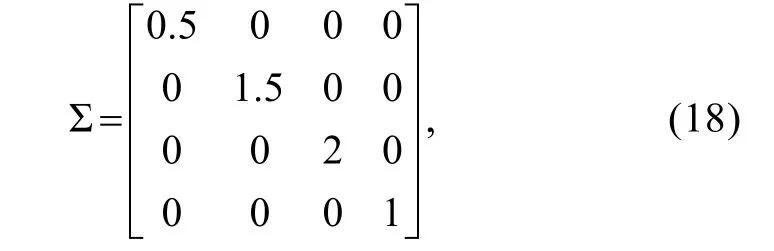

4.2 模拟作答

模拟作答时,首先根据参数“真值”和所选用的模型来计算被试

n

在项目

i

上的正确作答概率

P

。其次生成一个随机数

r

(0≤

r

≤1),则得分被定义为：

4.3 评价指标

采用平均偏差

Bias

、均方根误差

RMSE

和相对偏差的绝对值(the absolute value of relative bias,

ARB

)作为项目参数和题组效应参数返真性的评价指标：

采用属性判准率(attribute correct classification rate,

ACCR

)和属性属性模式判准率(pattern correct classification rate,

PCCR

)作为属性参数返真性的评价指标：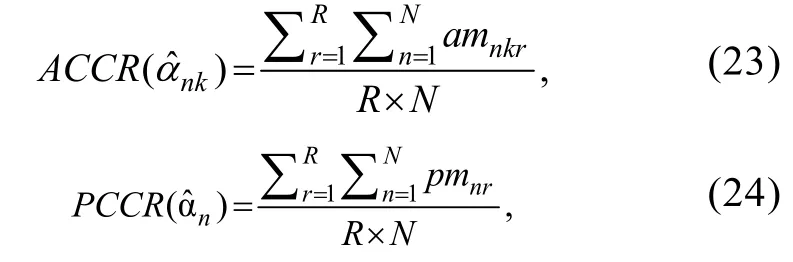

式中,

N

为样本容量,

K

为属性个数,

am

=1表示第

r

次循环中对被式

n

的第

k

个属性判断正确,

pm

=1表示第

r

次循环中被试

n

的掌握模式α判断正确。被试反应模拟及参数估计共循环

R

次以减小实验误差。

4.4 研究1结果与结论

研究1的结果见表2～表3和图3。其中,表2给出了研究1中

ACCR

和

PCCR

指标值,用于反映两个模型对目标属性的返真性。

表2 研究1中ACCRPCCR指标值

表3 研究1中对C-MTECDM的参数估计的返真性

注：为减少篇幅仅列出部分参数估计结果。

对于 C-MTECDM,当样本量为 1600时,其 5个属性的

ACCR

指标值分别为0.984、0.989、0.988和0.988,且

PCCR

指标值为0.958;当样本量增加至 3200时,其 5个属性的

ACCR

指标值分别为0.988、0.990、0.986、0.988和 0.988,且

PCCR

指标值为 0.960;当样本量增加至 4800时,

ACCR

和

PCCR

增幅较小。这说明C-MTECDM具有认知诊断功能,且判准率较高。而对于N-MTECDM,当样本量为1600时,其5个属性的

ACCR

指标值分别为 0.992、0.993、0.989、0.989,且

PCCR

指标值为 0.970。同样,

ACCR

和

PCCR

也会随着样本量的增加而增加,这同样说明N-MTECDM具有认知诊断功能。表3给出了研究1中C-MTECDM的题组效应参数方差、截距参数和属性权重参数的返真性。当样本量为1600时,题组效应参数方差的

Bias

指标值介于[–0.03 0.05]之间,

RMSE

指标值介于[0.07,0.10]之间,

ARB

指标值介于[0.01,0.04]之间均小于0.05,

SD

介于[0.07,0.11]之间;30个项目的截距参数的

Bias

指标值的平均值为0.04,

RMSE

指标值平均值为0.15,

ARB

指标值平均值为0.04,

SD

的平均值为0.15;60个属性权重参数的

Bias

指标值的平均值为0.04,

RMSE

指标值平均值为0.15,

ARB

指标值平均值为0.04,

SD

平均值为0.15。另外,表中已经将

ARB

指标值大于0.05的结果(表示该估计结果不可被接受)以粗体形式标记出,可以看出当样本量为1600时,不可接受的参数估计结果数为21个且主要集中在后面考查3个属性的题目的属性权重参数上,表明每个题目所考查的属性个数会影响C-MTECDM 的参数估计结果;随着样本量的增加,各个参数的估计精准度和稳定性均有所提升,当样本量提升至 3200时,不可接受的参数估计结果数为3;当样本量增加至4800时,参数估计的返真性表现更好,但增幅小于样本量从 1600增加至 3200时的增幅。因此欲实现C-MTECDM较为精准的参数估计,在与本研究研究条件相似的情况下,建议样本数量不低于3000。表4给出了研究1中N-MTECDM的题组效应参数方差、截距参数和属性权重参数的参数估计返真性。与C-MTECDM类似,4个评价指标值均随着样本量的增加而减小,即返真性随着样本量的增加而提高。根据

ARB

指标值,当样本量为1600时不可接受的参数估计值数量仅为3个,因此欲实现对N-MTECDM 较为精准和稳定的参数估计,在与本研究研究条件相似的情况下,建议样本数量不低于1500。同样可发现前 30个截距参数的估计返真性普遍高于后面的属性权重参数的估计返真性。

根据上述结果可知,(1)当样本量足够大时,参数估计程序可为C-MTECDM和N-MTECDM提供较精准和稳定的参数估计;(2)C-MTECDM 与N-MTECDM 均具有认知诊断功能,且均可有效处理题组效应。此外,当样本量为 4800时,C-MTECDM和N-MTECDM均有很好的参数估计结果,这为研究2进行模型对比提供了前提保障。

5 研究2

5.1 研究设计

研究2用于进行模型对比,即为读者呈现当作答数据包含题组效应时,使用不包含题组效应参数的LLM和(logit)DINA模型去进行数据分析所带来危害;以及当作答数据不包含题组效应时,使用MTECDM 去进行数据分析会得出什么结果。为简化研究,研究2所用Q矩阵、U矩阵、项目参数、题组效应与被试属性掌握模式等的设定均与研究1保持一致。

5.2 模拟作答以及评价指标

被试模拟作答以及评价指标与研究1大体一致,所不同的是：(1)在模拟作答时,当作答数据包含题组效应时,会使用MTECDM作为真实模型去生成作答数据;而当作答数据不包含题组效应时,会使用LLM或(logit)DINA模型作为真实模型去生成作答数据;(2)样本容量均设定为4800;(3)在研究2中还 添 加 了 –2

log-likelihood

(–2

LL

)、

AIC (

Akaike,1974)、

BIC (

Schwarz,1978)这3个相对评价指标：

(27)式中,

L

为似然函数,

d

为所采用模型估计参数的个数,

N

为被试样本量。这3个指标值越小表明模型-数据拟合越好。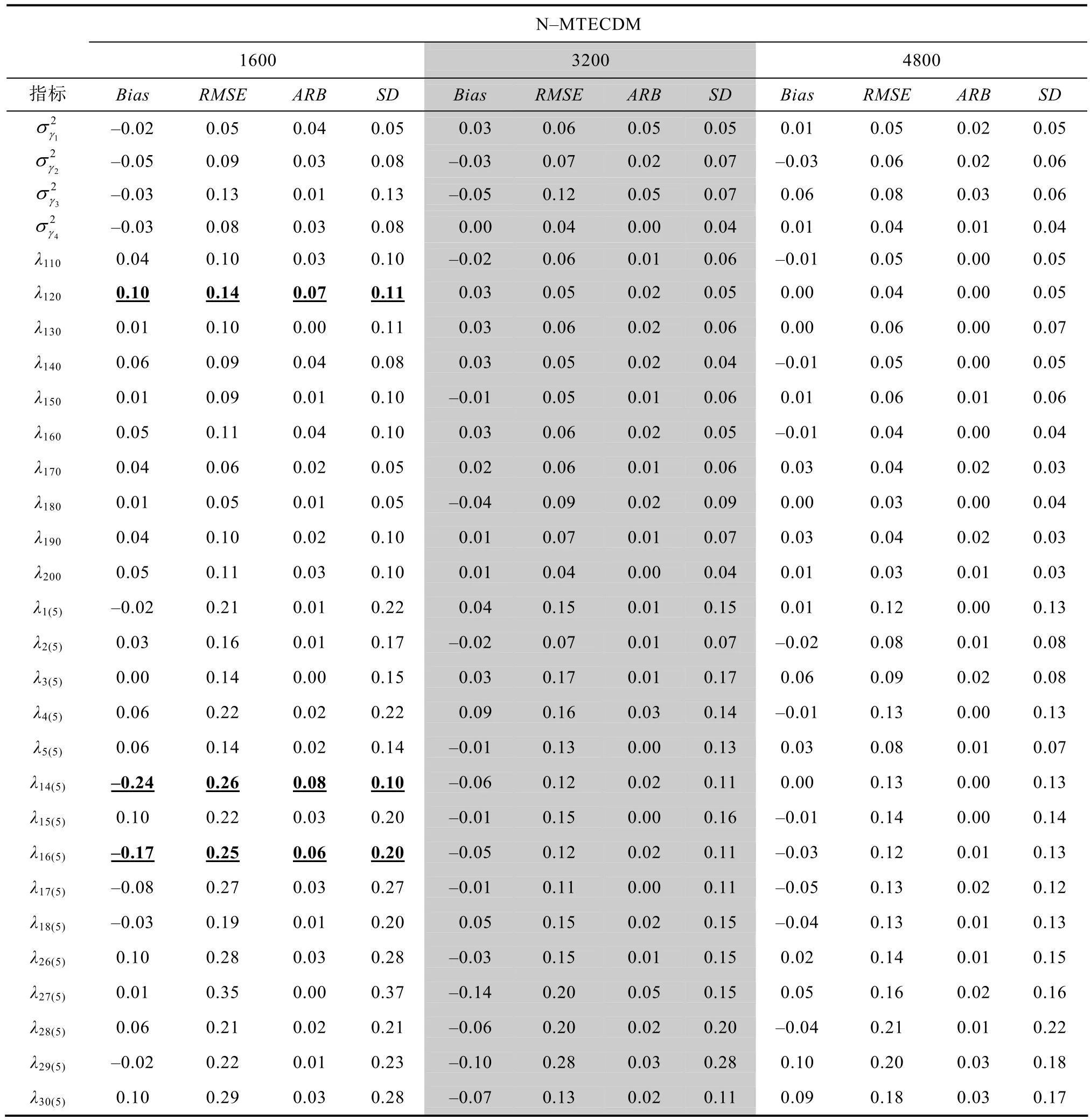

表4 研究1中对N-MTECDM的题组效应参数方差与截距参数的返真性

5.3 研究2结果与结论

研究2结果见表5和表6。其中,表5给出了LLM和C-MTECDM之间的对比结果,当真实模型为LLM时(即作答数据不包含题组效应),两个模型均有较好的参数返真性,且从各评价指标看,两者分析的结果间几乎无差异,至于为什么 C-MTECDM比LLM的

AIC

和

BIC

指标值还略小,这可能是由于模拟研究中的随机误差造成的(e.g.,4.2中模拟作答过程),而题组效应参数正是为了处理题组效应这一误差项而添加的;而当真实模型为 C-MTECDM时(即作答数据包含题组效应),仅有 C-MTECDM具有较好的参数返真性,而 LLM 无论对项目参数还是目标属性的返真性均较差。此时,C-MTECDM的-2

LL

、

AIC

和

BIC

指标值也显著小于LLM的,说明LLM对该作答数据的拟合度较差。表6给出了(logit)DINA和N-MTECDM之间的对比。实验结果和结论与上文类似,但与表4中结果不同的是,当使用(logit)DINA去分析含有题组效应的数据时,虽然参数估计偏差大、精确度低,但却有较好的稳定性。这或许也是因为C-MTECDM中

h

(·)的复杂性高于N-MTECDM中的

h

(·),所以导致在提供同等信息量的情况下 CMTECDM的参数估计返真性会低于N-MTECDM的,而又因为这两种模型对认知属性对正确作答概率贡献方式假设的不同,所以并不具有直接可比性,研究者需要根据不同的测验情境去选用适合的模型。

综上所述,(1)当作答数据含有题组效应时,采用忽略题组效应的LLM和(logit)DINA模型会导致项目参数的偏差估计并降低对目标属性的判准率,且(logit)DINA模型的参数估计稳定性高于LLM;(2)相对于LLM和(logit)DINA而言MTECDM更具普适性,即便当作答数据不存在题组效应时,测验分析采用MTECDM也能得到很好的参数估计结果。

表5 两个补偿模型(LLM与C-MTECDM)之间的对比

表6 两个非补偿模型((logit)DINA与N-MTECDM)之间的对比

max –0.30.82.27.16 0.10.22.03.23均ACCR0.962 0.997 PCCR0.891 0.986–2LL154236.10 128436.1 AIC154388.10 128598.1 BIC154837.90 129122.7

当然,研究 2的结论也提醒研究者,如果在以往的实证研究中曾使用了忽略题组效应的CDM去分析包含题组的CDA数据,则分析结果(尤其是对被试知识状态的判断)有可能与事实存在较大的偏差。但由于在实证研究中没有“真值”可作为参照,所以这种偏差往往会被忽视,即有可能高估了测验信效度。

6 总结与展望

目前,CDA作为教育与心理测量的研究热点得到了迅速发展,但纵观已有的 CDM 后发现它们都无法有效处理含有题组效应的测验数据。与此同时,题组也已经大范围出现在现实测验中,而已开发的TRM却不具有认知诊断的功能。因此,开发出一种即具有认知诊断功能的又能有效处理题组效应的项目反应模型是必要的。这不仅可以拓展CDA中的题型,亦可以进一步提高 CDA的效率。针对该问题,本文首先简单介绍了题组效应的相关概念和LLM,之后将多维题组效应向量参数与 LLM 相结合提出了属性间具有补偿作用的C-MTECDM和属性间具有非补偿作用的N-MTECDM。在研究1中探讨了两个新模型的参数返真性,根据研究结果认为：(1)当样本量足够大时,基于WinBUGS的参数估计程序可行有效,使MTECDM无论对项目参数还是目标属性的返真性均较好;(2)MTECDM 具有认知诊断功能,且均可有效处理题组效应。这为研究2进行模型对比提供了前提保障。在研究2中,通过与无法处理题组效应的LLM和(logit)DINA模型进行了对比研究,根据研究结果认为：(1)当作答数据含有题组效应时,采用忽略题组效应的 LLM 和(logit)DINA模型会导致项目参数的偏差估计并降低对目标属性的判准率;(2)MTECDM更具普适性,即便当作答数据不存在题组效应时,测验分析采用MTECDM 也能得到很好的参数估计结果。整体来看,MTECDM 合理有效,是对解决“开发出一种即具有认知诊断功能的又能有效处理题组效应的项目反应模型”这一问题的一种尝试。

Hansen (2013)结合 2-tier模型(Cai,2010)和LCDM 也提出了一种适用于认知诊断测验的题组模型。但由于 2-tier模型的限制,该模型要求每个题目最多只能归入 1个题组或特殊组维度(groupspecific dimension)之中(Hansen,2013),即仅能处理项目内单维题组效应,无法处理可能存在的项目内多维题组效应。经过简单地转换,该模型也可归入LTF (见式(12))之中。

当然,本研究还存在着些许值得今后进一步探讨的地方,如：(1)将分类变量的属性与连续变量的题组效应直接在 logit联接函数下进行连加是否合理还有待进一步验证;(2)MTECDM 本身并不涉及属性层级关系,所以当目标属性间存在明确的层级关系时,MTECDM的表现值得进一步探讨;(3)本文在使用WinBUGS软件对MTECDM进行参数估计时,各参数的先验分布均为自定义,今后仍需要根据实际数据的分析结果不断地对现有的先验分布进行修正;(4)目前MTECDM仅能处理二级评分数据,今后亦可考虑将MTECDM拓广至多级评分模型。

Akaike,H.(1974).A new look at the statistical model identification.

IEEE Transactions on Automatic Control,19

(6),716–723.Ackerman,T.A.(1994).Using multidimensional item response theory to understand what items and test are measuring.

Applied Measurement in Education,7

(4),255–278.Bradlow,E.T.,Wainer,H.,&Wang,X.H.(1999).A Bayesian random effects model for testlets.

Psychometrika,64

(2),153–168.Cai,L.(2010).A two-tier full-information item factor analysis model with applications.

Psychometrika,75

(4),581–612.DeMars,C.E.(2006).Application of the bi-factor multidimensional item response theory model to testlet-based tests.

Journal of Educational Measurement,43

(2),145–168.Hansen,M.(2013).

Hierarchical item response models for cognitive diagnosis

(Unpublished doctoral dissertation).University of California,LA.Hoogland,J.J.,&Boomsma,A.(1998).Robustness studies in covariance structure modeling:An overview and a meta-analysis.

Sociological Methods &Research,26

,329–367.Henson,R.A.,Templin,J.L.,&Willse,J.T.(2009).Defining a family of cognitive diagnosis models using log-linear models with latent variables.

Psychometrika,74

(2),191–210.Huang,H.-Y.,&Wang,W.-C.(2013).Higher-order testlet response models for hierarchical latent traits and testlet-based items.

Educational and Psychological Measurement,73

(3),491–511.Haertel,E.H.(1989).Using restricted latent class models to map the skill structure of achievement items.

Journal of Educational Measurement,26

(4),301–321.Junker,B.W.,&Sijtsma,K.(2001).Cognitive assessment models with few assumptions,and connections with nonparametric item response theory.

Applied Psychological Measurement,25

(3),258–272.Li,Y.,Bolt,D.M.,&Fu,J.(2006).A comparison of alternative models for testlets.

Applied Psychological Measurement,30

(1),3–21.Maris,E.(1999).Estimating multiple classification latent class models.

Psychometrika,64

(2),187–212.Rupp,A.A.,&Templin,J.L.(2007).

Unique characteristics of cognitive diagnosis models

.Paper presented at the annual meeting of the National Council on.Measurement in Education.Chicago,IL.Spiegelhalter,D.J.,Thomas,A.,&Best,N.(2003).

WinBUGS version 1.4

[computer software].Cambridge,England:MRC Biostatistics Unit,Institute of Public Health.Schwarz,G.(1978).Estimating the dimension of a model.

The Annals of Statistics,6

(2),461–464.Tatsuoka,K.(1985).A probabilistic model for diagnosing misconceptions by the pattern classification approach.

Journal of Educational Statistics,10

(1),55–73.Templin,J.L.,&Henson,R.A.(2006).Measurement of psychological disorders using cognitive diagnosis models.

Psychological Methods,11

(3),287–305.Wainer,H.,&Kiely,G.(1987).Item clusters and computerized adaptive testing:A case for testlets.

Journal of Educational Measurement,24

(3),185–202.Wainer,H.,Bradlow,E.T.,&Du,Z.R.(2000).Testlet response theory:An analog for the 3PL model useful in testlet-based adaptive testing

.

In W.van der Linden &C.A.W.Glas (Eds.),

Computerized adaptive testing:Theory and practice

(pp.245–269).London:Kluwer.Wainer,H.,Bradlow,E.T.,&Wang,X.(2007).

Testlet response theory and its applications

.New York:Cambridge University Press.Wang,W.-C.,&Wilson,M.(2005).The rasch testlet model.

Applied Psychological Measurement,29

(2),126–149.Yao,L.,&Boughton,K.A.(2007).A multidimensional item response modeling approach for improving subscale proficiency estimation and classification.

Applied Psychological Measurement,31

(2),83–105.Zhan,P.D.(2014).

The development and application of multidimensional testlet-effect models

(Unpublished master thesis).Zhejiang Normal University.[詹沛达.(2014).

多维题组效应模型的开发与应用

(硕士学 位论文).浙江师范大学.]Zhan,P.D.,Wang,W.-C.,&Wang,L.J.(2013).Testlet response theory:An introduction and new developments.

Advances in Psychological Science,21

(12),2265–2280.[詹沛达,王文中,王立君.(2013).项目反应理论新进展之 题组反应理论.

心理科学进展,21

(12),2265−2280.]Zhan,P.D.,Wang,W.-C.,Wang,L.J.,&Li,X.M.(2014).The multidimensional testlet-effect Rasch model.

Acta Psychologica Sinica

,

46

(8),1208–1222.[詹沛达,王文中,王立君,李晓敏.(2014).多维题组效应Rasch模型.

心理学报,46

(8),1208–1222.]