大规模M IMO时分双工系统的鲁棒预编码设计

顾浙骐魏 宁 张忠培

（电子科技大学通信抗干扰技术国家级重点实验室 成都 611731）

大规模M IMO时分双工系统的鲁棒预编码设计

顾浙骐*魏 宁 张忠培

（电子科技大学通信抗干扰技术国家级重点实验室 成都 611731）

对于采用大规模M IMO技术的时分双工系统，天线互易误差会破坏上下行信道互易特性，大幅降低预编码算法下行传输性能。由于实际系统难以完全消除天线互易误差，该文以最大化各用户平均信泄噪比为目标，根据天线互易误差的统计特性，设计了对该误差具有鲁棒性的线性预编码算法。同时为了进一步降低用户接收端的等效噪声功率，该文还将该线性鲁棒预编码算法扩展为基于矢量扰动的非线性鲁棒预编码算法，并通过减格辅助技术降低其扰动矢量求解复杂度，使其更适用于大规模M IMO系统应用。计算机仿真结果表明在存在基站天线互易误差条件下，该文所提出的线性与非线性鲁棒性预编码算法的性能均优于传统预编码算法的性能。

无线通信；大规模M IMO；信道互易误差；鲁棒预编码

1 引言

大规模M IMO（very large M IMO或massive M IMO）技术具有系统容量大、基站发射功率低、射频模块可移植性强、射频器件成本低等特点［1，2］。大规模M IMO系统的下行传输通常通过迫零（Zero Forcing， ZF）预编码、信泄噪比（Signal to Leakage and Noise Ratio， SLNR）预编码等线性预编码算法获得空间的复用增益［3］。而在实际大规模M IMO系统中，预编码算法性能严重依赖于下行信道状态信息（Channel State Information， CSI）的准确性。由于大规模M IMO技术的天线数远远超过传统M IMO技术，以至于频分双工（Frequency Division Duplex， FDD）系统的下行导频开销和量化反馈开销大幅增加。因此传统的FDD系统无法为大规模M IMO技术的下行CSI获取提供足够的时频资源。与之相比，时分双工（Time Division Dup lex， TDD）系统利用信道互易特性，使基站能通过上行导频估计获得下行信道CSI。其中上行导频开销正比于用户数而与基站天线数无关。因此TDD系统被认为更易于大规模M IMO技术的实现和应用［4］。为了表述方便，若非特殊说明，后文中的系统均表示TDD系统。

在实际系统中，上下行基带信道除了理想互易的空中传播信道外，还包括用户天线与基站天线的收发射频模块。由于收发射频模块包含的内部时钟、功放、锁相环等器件存在结构上和制造工艺上的差异，导致各射频模块具有不同的射频增益，即各天线具有随机的相位与幅度。特别对于采用低成本射频单元的大规模M IMO系统，射频模块的相位噪声、天线耦合等因素使上述现象变得尤为严重。因此，用户天线与基站天线的射频随机增益会造成大规模M IMO系统上下行基带信道的互易误差，通常被称为天线互易误差。文献［5］将天线互易误差建模为对角矩阵，其对角元素为时间，功率，温度的慢变函数。文献［6］分析了此类天线互易误差对常用预编码算法性能的影响。文献［7］指出天线互易误差会降低下行CSI估计的精度，同时通过推导大规模M IMO系统下行传输可达速率证明了其系统容量受限于天线互易误差的大小。文献［8］提出了基于数字信号处理的校准算法对天线互易误差进行补偿。然而，该算法受限于信道估计误差和量化反馈精度。在实际的大规模M IMO系统中，校准算法会消耗大量时频资源，同时也难以保证天线互易误差被完全消除［9］。

本文从预编码算法设计的角度去考虑如何降低天线互易误差对下行传输性能的影响。首先本文推导了大规模M IMO系统存在天线互易误差条件下，各用户的信泄噪比。然后以最大化各用户平均信泄噪比为目标，利用天线互易误差的统计特征，设计了对该误差具有鲁棒性的线性预编码算法。为了更好地降低用户接收端的等效噪声功率，本文还将该线性鲁棒预编码算法扩展为非线性鲁棒预编码算法，并通过减格辅助技术降低其复杂度，使其更适用于大规模M IMO系统。最后，通过计算机仿真验证了本文算法的性能。

2 天线互易误差模型

假设系统由一个配置NB根天线的基站和NM个配置单天线的用户组成。如图1所示，基站和用户间的上下行基带信道可表示为

图1 上下行等效基带信道模型

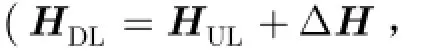
3 基于SLNR的鲁棒预编码设计

3.1 存在天线互易误差的下行传输各用户SLNR分析

对于使用线性预编码下行传输，用户的接收向量y可表示为

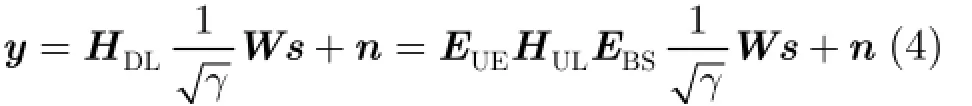
用户k的SLNR可表示为

3.2 线性鲁棒预编码设计

由于 EUE对下行传输性能无影响，所以令EUE= I。用户k的SLNR，即式（5b）可被改写为

由功率控制因子γ约束基站下行传输的发射功率，则对于存在基站天线互易误差的大规模M IMO系统，用户k的预编码向量可通过求解最优化问题式（7）获得

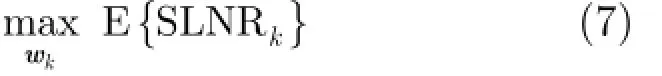
3.3 非线性鲁棒预编码设计

根据图2所示，类似式（4），用户端的接收向量y'的表达式为

图2 基于矢量扰动的非线性鲁棒预编码

在实际的大规模M IMO系统中，扰动矢量求解的复杂度会成为实现该非线性鲁棒预编码的主要障碍。在此，本文引入栅格理论和减格辅助技术（Lattice Reduction Aid， LRA）降低上述扰动矢量求解的复杂度。针对某栅格寻找其相对短且几乎正交的基（缩减基）的过程被称为栅格基缩减，即为LRA技术［15］。当栅格的基向量近似正交时，则可以通过栅格理论中的最近点取整近似（closest-point approximation）获得式（13）问题的近似解，而避免高复杂度的搜索求解［15］。作为一种数学方法，LRA技术已有较多成熟算法。较为常用的LRA算法是Lenstra A K， Lenstra H W和 Lovász L在1982年提出的LLL减格算法［16］。本文基于LLL减格算法基本思想，求解式（12）中的扰动矢量p近似值。该扰动矢量p近似值求解算法如表1所示。

表1 扰动矢量近似求解

4 计算机仿真及结果分析

本章通过计算机仿真验证本文所提出的线性鲁棒预编码以及非线性鲁棒预编码的性能。假设基站天线数NB= 4，用户数NM= 4。基站与用户间的空中信道H为瑞利衰落（Rayleigh fading）信道。假设上行信道HUL= H。忽略用户天线互易误差（即EUE= I），同时令基站天线互易误差矩阵 EBS为对角阵，其对角线元素相互独立且同分布。各对角元素的幅度服从均匀分布U（-A， A），其中A的单位为dB。各对角元素的相位服从均匀分布U（-θ，θ），其中θ的单位为度（°）。根据式（3），下行信道HDL= HEBS。在仿真中，各用户均采用QPSK调制方式。假设上行信道 HUL和基站天线互易误差的自相关矩阵 RBS理想已知，则仿真可以根据第3节所述的3种鲁棒预编码算法计算出对应的预编码向量和预编码矩阵W。经过下行信道 HDL和噪声叠加n，由式（4）和式（11），用户k的信干噪比SINRk可表示为

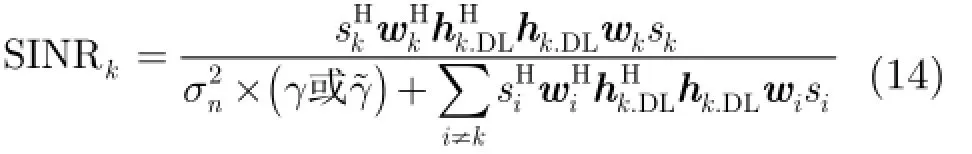
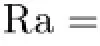
图3 A=2 dB， 20θ=°预编码算法平均可达和速率

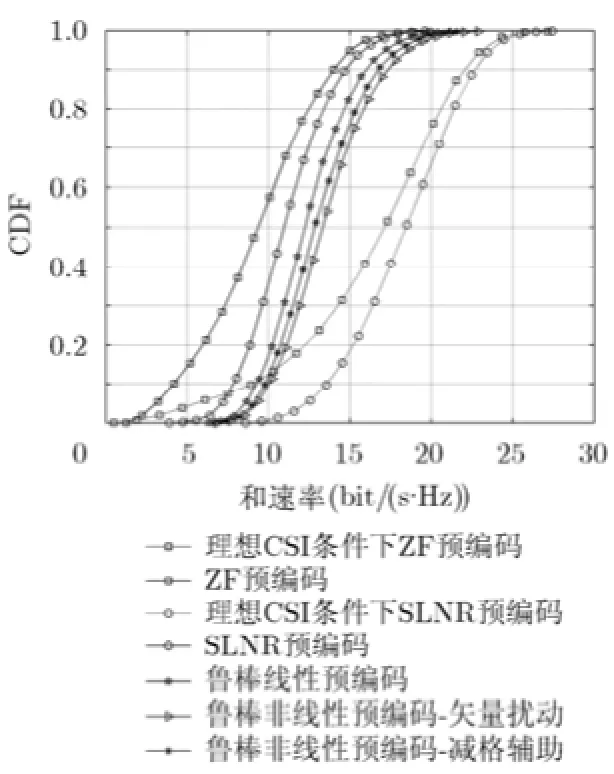
图4 A =2 dB， 20θ=°，ρ=20 dB， 预编码算法可达和速率CDF

图5 A =3 dB， 30θ=°预 编码算法平均可达和速率

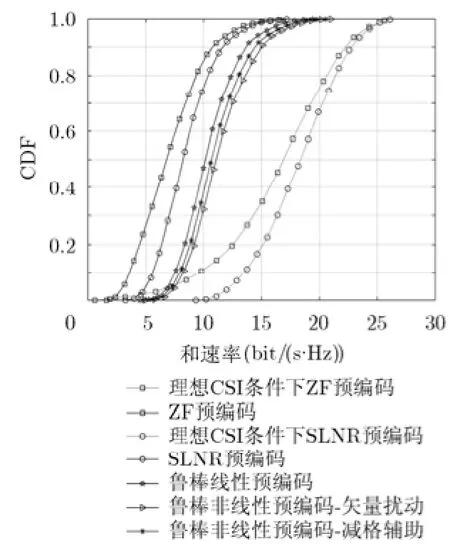
图6 A=3 dB， θ=30°，ρ=20 dB预编码算法可达和速率CDF

图7 A=2 dB， 20θ=°预编码算法误码率

图8 A=3 dB， 30θ=°预编码算法误码率

图4和图6分别表示当A=2 dB， θ=20°和A=3 dB， θ=30°时，同时ρ=20 dB ，各预编码算法可达和速率的积累分布函数（Cum u lative Distribution Function， CDF）曲线。当A=2 dB，θ=20°时，线性鲁棒预编码能获得相对于SLNR预编码高1.5 bit/（s· Hz）的平均可达和速率。当A=2 dB， θ=20°时，线性鲁棒预编码能获得相对于SLNR预编码高2 bit/（s· Hz）的平均可达和速率。所以尽管随基站天线互易误差增大，所有预编码算法的性能均下降，但本文所设计的线性和非线性鲁棒预编码相较于传统的ZF和SLNR的性能下降的幅度更小。同时，在基站天线互易误差存在时，由于非线性鲁棒预编码减小了等效噪声的功率，所以能取得比线性鲁棒预编码更好的性能。由于LRA技术对扰动矢量进行了近似求解，基于LRA技术的非线性鲁棒预编码相较于基于搜索的非线性鲁棒预编码有一定的性能损失。但基于LRA技术的非线性鲁棒预编码的可达和速率仍然高于线性鲁棒预编码。

根据图2所示的下行传输流程，通过仿真，我们可以得到当无信道编码，采用QPSK调制，并存在基站天线互易误差时，各预编码算法的误码率。图7和图8分别表示当A=2 dB， θ=20°和A=3 dB，θ=30°时各预编码算法的误码率曲线。当信噪比较低时，由于非线性鲁棒预编码的非线性操作造成的取模损失（m odule loss）和功率损失（power lose）［14］，所以非线性鲁棒预编码的误码率会略高于线性鲁棒预编码和传统SLNR预编码的误码率。当信噪比较高时，图7和图8的仿真结果和前文的性能分析结果保持一致，随信噪比的增加，非线性鲁棒预编码的误码率比线性鲁棒预编码的误码率下降得更快。

5 结束语

对于采用大规模M IMO技术的TDD系统，基站天线的互易误差会破坏上下行信道互易特性，大幅降低传统预编码算法下行传输性能。由于实际系统难以完全消除天线互易误差，本文以最大化各用户平均SLNR为目标，利用天线互易误差的统计特征，设计了对该误差具有鲁棒性的线性预编码算法。同时为了进一步降低用户接收端的等效噪声功率，本文还将该线性鲁棒预编码算法扩展为基于矢量扰动的非线性鲁棒预编码算法，并通过LRA技术降低其扰动矢量求解复杂度，使其更适用于大规模M IMO系统应用。计算机仿真结果表明当基站天线互易误差存在时，本文所设计的线性和非线性鲁棒预编码能获得较传统的ZF和SLNR预编码算法更好的下行传输性能，对基站天线互易误差具有一定的鲁棒性。

［1］ Larsson E G， Tufvesson F， Edfors O， et al.. Massive M IMO for next generation w ireless system s［J］. IEEE Communications Magazine， 2014， 52（2）: 186-195.

［2］ Hoydis J， Ten Brink S， and Debbah M. Massive M IMO in the UL/DL of cellular networks: how m any antennas do we need［J］. IEEE Journal on Selected Areas in Comm un ications， 2013，31（2）: 160-171.

［3］ Lu L， Li G， Sw indlehurst A， et al.. An overview of massive M IMO: benefits and challenges［J］. IEEE Journal of Selected Topics in Signal Processing， 2014， 8（5）: 742-758.

［4］ Rusek F， Persson D， Buon Kiong Lau， et al.. Scaling up M IMO: opportunities and challenges w ith very large arrays［J］. IEEE Signal Processing Magazine， 2013， 30（1）: 40-60.

［5］ A lcatel-Lucent. Channel recip rocity m odeling and performance evaluation， R1-100426［R］. 3GPP TSG RAN WG1 59 meeting， Valencia， 2012.

［6］ Huang Fan， Wang Ya-feng， and Geng Jian. Antenna m ism atch and calibration problem in coordinated mu lti-point transm ission system［J］. IET Comm unications， 2012， 6（3）: 289-299.

［7］ Björnson E， Hoydis J， Kountouris M， et al.. Massive M IMO system s w ith non-ideal hardware: energy efficiency，estimation， and capacity lim its［J］. IEEE Transactions on Inform ation Theory， 2014， 48（3）: 126-139.

［8］ Shepard C， Yu H， Li E， et al.. A rgos: practical m any-antenna base stations［C］. Proceedings of the 18th Annual International Conference on M obile Computing and Networking， New York， USA， 2012: 53-64.

［9］ Rogalin R， Bursalioglu O Y， Papadopoulos H C， et al.. Hardware-impairm ent com pensation for enabling d istributed large-scale M IMO［C］. 2013 Inform ation Theory and App lications Workshop （ITA）， San D iego， USA， 2013: 1-10 .

［10］ 王海荣， 王玉辉， 黄永明， 等. 大规模 M IMO 多小区 TDD系统中的导频污染减轻方法［J］. 信号处理， 2013（2）: 171-180. Wang Hai-rong， Wang Yu-hui， Huang Yong-m ing， et al.. Pilot contam ination reduction in very large M IMO multi-cell TDD systems［J］. Journal of Signal Processing， 2013（2）: 171-180.

［11］ 3GPP， TS 36.211. Physical channels and m odulation［S］. 2010.

［12］ 张贤达. 矩阵分析与应用［M］. 北京: 清华大学出版社， 2004: 528-538. Zhang X ian-da. M atrix Analysis and App lications［M］. Beijing: Tsinghua University Press， 2004: 528-538.

［13］ Sadek M and Aissa S. Leakage based p recoding for multi-user M IMO-OFDM system s［J］. IEEE Transactions on W ireless Communications， 2011， 10（8）: 2428-2433.

［14］ M aurer J， Jaldén J， Seethaler D， et al.. Vector perturbation precoding revisited［J］. IEEE Transactions on Signal Processing， 2011， 59（1）: 315-328.

［15］ Conway J H and Sloane N J A. Sphere Packings， Lattices and Groups［M］. 3rd Edition， New York， Springer-Verlag， 1999: 206-238.

［16］ Lenstra A K， Lenstra H W， and Lovász L. Factoring polynom ials w ith rational coefficients［J］. Mathematische Annalen， 1982， 261（4）: 515-534.

［17］ Hassibi B and Vikalo H. On the expected com p lexity of integer least-squares problem s［C］. IEEE International Con ference on Acoustics， Speech （ICASSP）， Orlando， USA，2002: 1497-1500.

顾浙骐： 男，1984年生，博士，研究方向为协作通信、预编码、信道互易性.

魏 宁： 男，1979年生，副教授，博士，研究方向为无线通信、空时编码.

张忠培： 男，1967年生，教授，博士生导师，博士，研究方向为无线通信、信道编码.

Robust Precoding in M assive M IMO Time Division Dup lex System s

Gu Zhe-qi Wei Ning Zhang Zhong-pei
（National Key Laboratory of Science and Techno logy on Communication， University of
Electronic Science and Technology of China， Chengdu 611731， China）

The down link transm ission performance of the massive M IMO Time Division Dup lex （TDD） system is bottlenecked by the channel reciprocity errors called antenna reciprocity errors. Antenna reciprocity errors are hard to be calib rated com p letely in practical system s. In order to avoid the perform ance degradation of the down link transm ission， a linear robust p recoding algorithm is proposed， which can maxim ize each user’s average Signal to Leakage and Noise Ratio （SLNR） by using the statistical characteristics of the antenna recip rocity errors. To further reduce the equivalent noise power of users， the linear robust precoding algorithm is im proved into nonlinear robust precoding algorithm by vector perturbation. Lattice reduction aid is also used to reduce the comp lexity of the perturbation vector search， and make the nonlinear robust precoding algorithm be availab le for the massive M IMO. Simu lation results show that the proposed linear and non linear robust p recoding algorithm s can achieve better performance than the traditional Zero Forcing （ZF） and SLNR p recoding algorithm s when antenna recip rocity errors exist.

W ireless communication； Massive M IMO； Channel reciprocity errors； Robust p recoding

TN92

： A

：1009-5896（2015）05-1180-07

10.11999/JEIT 141073

2014-08-11收到，2014-12-26改回

国家自然科学基金（61101092）和国家863计划项目（2014AA01A 704）资助课题

*通信作者：顾浙骐 guzheqi@163.com