一种距离扩展目标的Hough变换检测器

问 翔刘宏伟*包 敏

①（西安电子科技大学雷达信号处理国家重点实验室 西安 710071）

②（西安电子科技大学电子工程学院 西安 710071）

一种距离扩展目标的Hough变换检测器

问 翔①刘宏伟*①包 敏②

①（西安电子科技大学雷达信号处理国家重点实验室 西安 710071）

②（西安电子科技大学电子工程学院 西安 710071）

针对宽带雷达信号得到的距离扩展目标在有较大运动速度时积累检测困难的问题，该文提出一种基于Hough变换的检测器（HTD）。利用距离扩展目标高分辨距离像信号的相邻回波之间信号具有较大相关系数这一特点，在互相关序号与相关时间2维平面使用Hough变换进行积累来检测目标。理论推导表明Hough变换检测器不需要目标散射中心分布的先验知识和目标的运动信息，具有恒虚警（CFAR）性能。计算机仿真实验表明Hough变换检测器具有比不依赖散射中心分布信息的广义似然比（NSDD-GLRT）检测器更好的检测能力。

雷达信号处理；距离扩展目标；目标检测；恒虚警；Hough变换

1 引言

宽带信号极大地提高了雷达的距离分辨率，目标上的散射中心沿着雷达径向分布在多个距离分辨单元内，形成了距离扩展目标信号。对于高速运动的空中目标和空间目标，脉冲之间的目标距离走动给积累检测带来了困难。目前大多数距离扩展目标多脉冲积累检测算法都假设在检测的相关处理时间内目标相对雷达没有运动，或运动的多普勒导向矢量已知［115］-。而实际当中是无法做到的。

宽带雷达的1维高分辨距离像在相邻回波之间具有较高的相关性［16，17］，各次回波与其前一个回波的相邻相关序列组成的相关序号与相关时间2维平面上，目标运动会引起相关序列最大值形成特定曲线。利用这一几何特性，使用Hough变换来对目标能量进行积累检测。由此本文提出了一种基于Hough变换的距离扩展目标检测器（Hough Transformation Detector， HTD）。计算宽带雷达相邻回波的互相关序列，在相关序号与相关时间2维平面上进行Hough变换来积累目标能量并检测。本文提出的检测器降低了对目标距离单元走动的敏感性，不需要目标散射中心分布和运动的先验信息。理论分析表明在高斯复噪声背景下，检测门限与信噪比无关，具有恒虚警性能。计算机仿真实验验证了理论计算的结果，通过与NSDD-GLRT （Non-Scatterer Density Dependent Generalized Likelihood Ratio Test）检测器的性能比较，表明Hough变换检测器具有更好的检测能力。

2 距离扩展目标相邻相关的运动特性

2.1 回波中有目标信号且无越距离单元徙动时距离扩展目标信号的相邻相关性

宽带雷达目标相邻回波之间的1维高分辨距离像具有较高的相关性［16，17］。各次回波与前一次回波互相序列形成的相关序号与相关时间2维平面上，目标的运动使得互相关序列最大值出现不同的几何特征。下面理论推导这一几何特性。

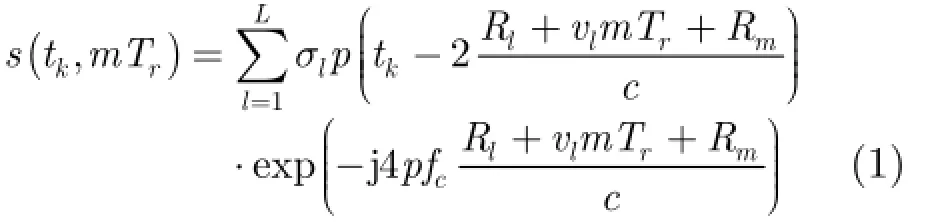
其中tk为脉冲发射时刻起计算的快时间，fc为雷达工作频率，c为电磁波传播速度，σl为目标上第l个散射中心的散射强度，vl为该散射中心在脉冲积累时间内的相对雷达的径向速度，p（ tk）为发射信号的复包络，回波包络中的时间延迟项2vm Tr/ c引起了回波包络的在距离上的整体走动，vl则引起散射中心在不同回波之间的越距离单元徙动。计算回波对快时间的傅里叶变换为

不同散射中心相对移动速度较小且在脉冲重复周期较小的情况下，相对移动速度与脉冲重复周期的相乘可以忽略，代入Al（ f），式（4）积分项目的后面两个中括号可以写为

式（5）第1部分为目标上所有散射中心散射能量的叠加，第2部分为每个强散射中心散射能量相对雷达坐标系的矢量和。式中第2个相位项中的分子为不同散射中心相对雷达距离差，分母为电磁波速度，分子与分母相比较小，第2个相位项可以忽略。若记式（5）求和的结果为E，则相邻回波互相关序列可以写为

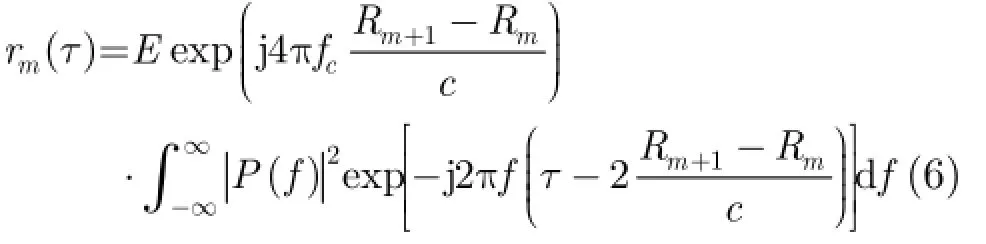
高距离分辨雷达一般采用大时宽带宽积的线性调频信号，其能量谱近似为宽度为带宽的矩形，脉冲压缩后每个散射中心回波包络信号为一个Sinc函数。由此式（6）可进一步整理为

互相关序列最大值的幅度为

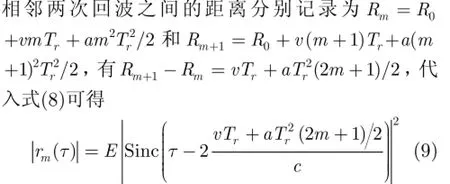
目标在相参处理时间内做匀速和匀加速运动时，相邻回波互相关序列最大值在相关序号和相关时间2维平面内是一条直线。匀速运动是垂直线，速度大于0时位于平面的右边，速度小于0时位于在平面的左边。当目标不动或速度较小可忽略时，垂直线在平面中间。当目标做匀加速运动时，相邻回波互相关序列最大值在相关序号与相关时间2维平面上为一条斜线。加速度大于0时，为斜率大于0的斜线。小于0时为斜率小于0的斜线。使用Hough变换在相邻相关序号和相关时间的2维平面上可对目标能量进行积累。

2.2 回波中有目标信号且存在越距离单元徙动时距离扩展目标信号的相邻相关性

当存在目标相对雷达转动引起的散射中心越距离单元徙动时的情况较为复杂。此时式（4）中后面2个中括号中的相位项不可忽略，将2个相位项展开有

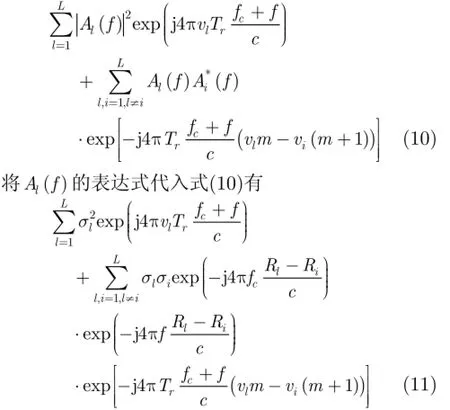
式（11）中第2个求和项的第2个相位项分子与分母相比较小可以忽略。当散射中心运动速度较大时，引起了回波之间的越距离单元徙动，式（11）中的多频率项不可忽略。多个频率项与发射信号频率函数的卷积引起混叠，将降低相邻回波之间的相关性。

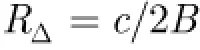
2.3 回波中没有目标信号时宽带信号的相关性

本文讨论的雷达是以在太空中运行的卫星和弹道导弹等为探测目标的远程雷达。没有目标信号时信号处理的检测器端主要是各类噪声的叠加，概率密度分布可用高斯分布进行描述。两次回波之间可看做相互独立的高斯随机变量［18］。设在没有目标回波时第M次与第M+1回波信号分别为xm（ t）和xm+1（ t ），噪声为均值为0方差为σ2的复高斯随机过程，自协方差函数为σ2δ（τ）。记第M次与第M+1回波信号经匹配滤波后的输出分别为，由随机变量理论可得［18］ym（ t）和ym+1（ t ）的均值和方差分别为的互协方差函数为

两次回波之间的噪声是相互独立的，式（12）有Cymym+1（τ）=0，没有目标回波时相邻两次回波的互相关序列为0。但在实际的工程中，是对真实协方差序列进行估计，估计值渐进收敛到真实值，收敛的程度与样本长度有关。样本数量是有限的，实际应用中的协方差序列估计值不是严格地等于0。

3 基于Hough变换的距离扩展目标检测器

3.1 使用傅里叶变换计算互相关序列

使用时域方法计算两个相互独立的高斯复噪声信号互相关序列，当相关时间较大时，中心极限定律适用。但当相关时间较小时，中心极限定律不适用，概率分布情况较为复杂，检测门限设置较为困难。为了避免这个问题，采用频域方法来计算回波之间的相关序列。

若回波脉冲点数为N，在没有目标信号时，回波是均值为0方差为σ2的相互独立的复高斯随机变量。进行回波能量归一化处理，随机变量是均值为0方差为1/2N的独立复高斯噪声。补N-1个0后均值不变，方差变为1/（4N- 2）。进行2N- 1点傅里叶变换，变为均值为0，实部和虚部的方差为0.5的复高斯随机变量。乘上相关时间向量不影响随机变量的概率分布。使用快速傅里叶变换进行相关运算的公式为

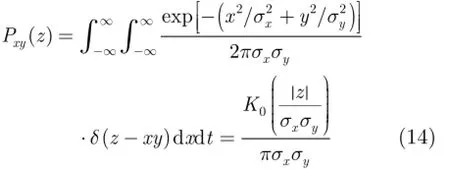
3.2 检测门限设置

复高斯随机变量的幅度为瑞利分布，在没有目标回波的情况下，按瑞利分布计算检测门限，需要计算多个瑞利分布随机变量和的概率分布，无法得到数学表达式。本文采用相关系数绝对值的平方作为检测统计量。参数为σ2的瑞利分布随机变量的平方服从参数为2σ2的指数分布。在进行Hough变换前，对幅度取平方变为参数为1的指数分布。M个参数为1的指数分布随机变量的和的概率密度函数为

当脉冲积累数为M，虚警概率Pf与检测门限的关系为按照这一公式，可以计算虚警率对应的检测门限。检测门限只与虚警率有关，可做到恒虚警检测。

常规的Hough变换按照极坐标方式来构建变换的参数空间。本文根据距离扩展目标检测的需要，使用直角坐标的参数空间来进行变换。如果有M次回波，则回波的相关序号与相关时间平面为M-1行2N- 1列，运算量较大。设置第1级检测门限，只对超过门限的平面点进行Hough变换，可以减少运算量。本文按照式（16）设置一级检测门限的虚警率为10-1，二级门限的虚警率为10-4。

3.3 检测器算法流程

由上面的分析推导可得基于Hough变换的距离扩展目标检测器（HTD）算法步骤为：

步骤1 接收到M次回波信号，每次回波信号经过Dechirp处理并离散采样为长度为N点的序列；

步骤2 每次回波补N-1个零点，构成2N- 1点的序列，进行2N- 1点的FFT；

步骤3 每次回波乘上对应的相关时间向量并与前一次回波的2N- 1点的FFT共轭相乘，得到互相关序列；

步骤4 互相关序列幅度与第1级门限进行比较，记录超过第1级门限元素的行列与幅度；

步骤5 对超过第1级门限的元素进行参数空间为直角坐标系的Hough变换；

步骤6 对Hough变换的最大值与第2级检测门限比较做出是否有目标的判决。

3.4 运算量分析

使用FFT在频率域计算互相关序列的步骤是计算M次回波的FFT，然后相邻回波的FFT序列共轭相乘后与相关时间向量相乘求和。为了便于FFT计算，一般补N个零，实际计算为2N点的FFT。计算2N点FFT需要进行Nlog2（ 2 N）次复数乘法和2N log2（ 2 N）次复数加法。计算一个相关序列值需要4N次复数乘法和2N- 1次复数加法。用FFT在频率域计算M次回波的M-1个互相关序列需要MNlog（ 2 N）+4 N2（ M- 1）次复数乘法和

2 2N log2（ 2 N）+（ M-1）（ 2 N- 1）2次复数加法。则一共需要进行的运算为4MN log（ 2 N）+16 N2（ M- 1）次

2实数乘法和4N（ M+2）log2（2 N）+2（ M-1）（8 N2- 4 N -1）次实数加法。

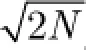
经典的NSDD-GLRT检测器需要进行12MN +12N+4次实数乘法、8MN- 4次实数加法和N次对数运算。相比较而言，本文提出的HTD检测算法的流程相对复杂，运算量也与第1级检测门限的设置有关，计算运算量也相对麻烦，比NSDD-GLRT检测器运算量要大。

4 仿真实验

本节对HTD检测器的性能进行实验验证，并与NSDD-GLRT检测器进行比较。

4.1 复高斯随机变量相互相关系数的概率分布

本小节对使用FFT计算相互独立的高斯复随机变量互相关序列的概率分布情况进行实验。按照3.1节的推导，两个长度为N点的相互独立的高斯复随机变量，在补1N-个0后进行傅里叶变换，乘上相关时间向量后对应相乘相加得到的复相关时间变量，实部和虚部应该服从均值为0方差为0.5N-的高斯分布。按照上述步骤生成两个N个点的复高斯随机白噪声向量，能量归一化并补1N-个0后，傅里叶变换计算互相关序列的相关时间复变量，统计实部和虚部组成的2N-个样本的均值、方差、偏度系数和峰度系数。设N分别为50， 64， 128和256。每个采样点数各进行106次实验，将各次实验的结果取平均作为最后的结果，如表1所示。

由表1的实验结果可见，均值、方差和偏度系数与高斯分布的非常接近，但是峰度系数略有差别。可见，经过运算处理的数据，基本上满足高斯分布要求。

4.2 对不同散射中心模型及不同运动形式的检测能力

设检测窗采样点数N=50，目标上的强散射中心数分别为j=3， 4， 5和10。设一个散射中心占据一个距离单元，脉冲积累数分别为M=4， 8， 16和32。对不同散射中心模型，在匀速运动和匀加速运动下分别进行实验，在每一个信噪比情况下进行104次实验。匀速运动实验结果如图1所示，匀加速运动情况下的实验结果如图2所示。图3为相同散射中心模型在不同运动情况下的对比。在匀速运动情况下，考虑目标上不同散射中心之间相对雷达除了径向上的运动外，还有转动的情况。此时目标上不同散射中心具有不同的微多普勒频率。设目标相对雷达的径向速度为300 m/s，相邻回波之间包络整体平移2.4个距离分辨单元。当目标上散射中心有微多普勒运动时，相对目标转动引起的散射中心在相邻回波之间的越距离分辨单元徙动为1个距离分辨单元，目标上有一个散射中心出现越距离单元徙动，其他的散射中心因为微多普勒频率出现幅度上的微小变化，变化范围为散射强度的1/10。对j=4，5在脉冲积累数M=4， 8情况下进行HTD有效性的实验，并与没有散射中心微多普勒频率的情况进行比较，实验结果如图4所示。

由图2和图3的结果可见，随着信噪比的增加，HTD的检测性能逐渐上升。对于不同散射中心模型的目标回波信号，检测率曲线非常接近，HTD检测器对散射中心模型不敏感。但是随着脉冲积累数的增加，检测率的增加并没有达到3 dB。为了便于计算检测门限，将各次回波互相关系数的平方后作为检测统计量。取平方后使得相关系数有所降低，相加后造成了积累损失，因此Hough变换的距离扩展目标检测器的积累检测性能改善没有能达到理论的结果。

表1 复高斯性实验结果

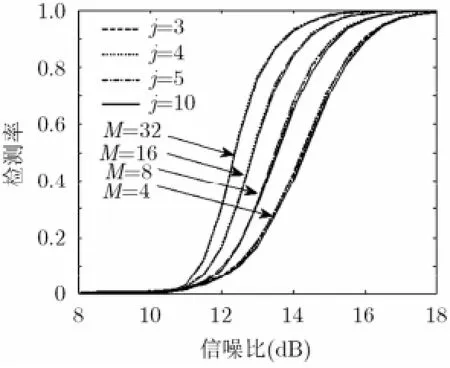
图1 匀速运动情况下对不同散射模型的HTD检测性能图

图2 匀加速运动情况下 HTD检测性能

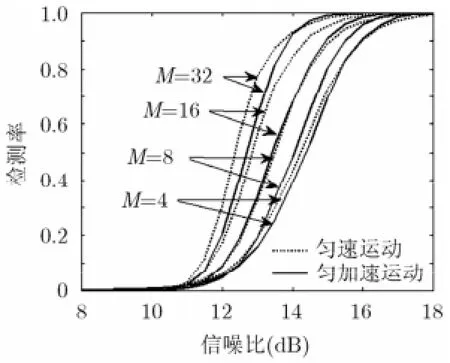
图3 4j=时匀速运动与 匀加速运动的对比

由图3可见，HTD对匀速运动的检测性能要比匀加速运动的好，在检测率为90%的地方，对匀速运动目标比匀加速运动目标的检测率要高约0.3 dB。仿真实验假设的检测窗采样点数为N=50，两个回波的互相关序列数据为99个数据点。当脉冲积累数分别是M=4， 8， 16和32时，得到的互相关序号与互相关平面的点数分别为3×99， 7×99， 15×99和31×99。可见是一个较为狭长的平面。在这样的平面上，Hough变换检测垂直线要比斜线容易。因此对于匀速运动的目标的检测率也就要高于对匀加速运动的目标。

由图4的实验结果可见，当散射中心之间存在不同的微小运动，产生不同的微多普勒频率时，相邻回波包络之间的相关性降低，使得HTD检测器的检测性能下降。与没有散射中心微动情况时相比，在检测率为90%的地方，分别下降了约6 dB和7 dB。并且因为相关性受到散射中心微动的影响，脉冲积累的效果也比没有散射中心微动时的效果差。

4.3 与NSDD-GLRT检测器的性能对比

本小节对比HTD检测器与NSDD-GLRT检测器的检测性能。NSDD-GLRT检测器是一种在具有二次形式的非高斯分布杂波或噪声背景下，利用广义似然比推导的距离扩展目标检测器。NSDDGLRT不需要知道目标散射中心分布的先验信息，但需要已知目标的运动向导矢量，或是可以通过高精度的估计得到。仿真实验中目标相对雷达做匀速运动，目标的导向矢量可以高精度的估计得到。本小节仿真实验的雷达参数与4.2小节的雷达参数相同。仿真实验中检测窗采样点数为N=50，设目标上强散射中心占据的距离单元数为j=5个。在脉冲积累数为M=16和32时，每个信噪比下进行104次实验，结果如图5所示。

图4 4，5j=匀速运动有无散射中心微动的比较

由图5的结果可见，随着信噪比的增加，HTD检测器的检测性能要比NSDD-GLRT检测器的检测性能有较大的改善。在检测率为90%时，约有3 dB的改善。NSDD-GLRT检测器没有利用目标运动的相关信息，而HTD检测器则利用了目标运动的信息，且NSDD-GLRT检测器积累了一些没有目标回波信号，而含有噪声信号的单元。因此HTD检测器的检测性能要比NSDD-GLRT检测器的好。

在进行本小节的计算机仿真实验时，对HTD检测器和NSDD-GLRT检测器的运算量时间进行了统计。计算完成信噪比在20 dB时从第1次回波完成能量归一化后到做出检测判决过程的104次计算机仿真实验所需要的时间，平均后作为检测器算法的运算时间。仿真实验在PC计算机上进行，计算机处理器为Intel（R）E7400，主频2.8 GHz，仿真软件为MALAB2012a。在运行仿真程序的同时，计算机同时还在运行其他程序和软件系统，结果保留小数点后4位。对比结果如表2所示。

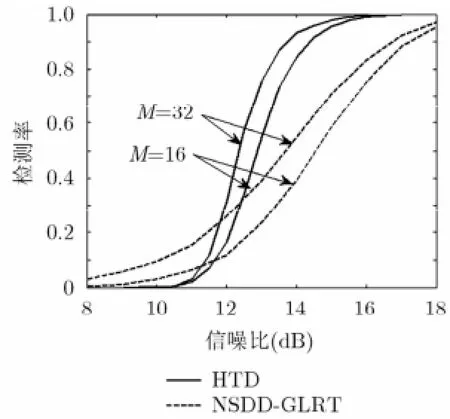
图5 HTD检测器与NSDD-GLRT检测器 的检测性能比较（5j=，匀速运动情况）

由表2的结果可见，随着脉冲数的增加，HTD与NSDD-GLRT的运算时间都有所增加，但是NSDD-GLRT的增加不是很多，而HTD的则增加了2.86倍。当脉冲积累数为M=16和M=32时，HTD的运算时间分别是NSDD-GLRT的5.47倍和15.08倍。

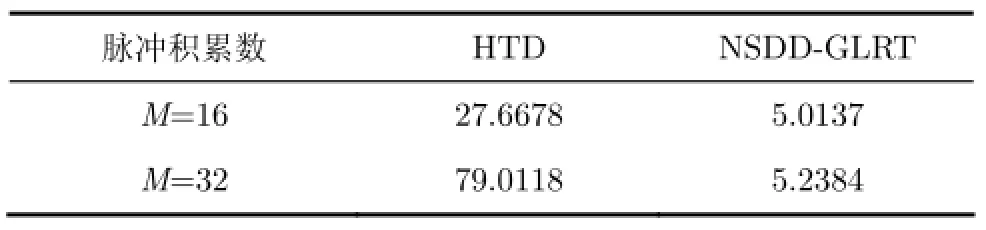
表2 HTD与NSDD-GLRT在20 dB时运算时间比较（m s）

5 结束语

利用宽带雷达信号得到的距离扩展目标信号相邻回波之间具有较大相关性这一特点，在相关序号与相关时间2维平面利用Hough变换来进行目标信号的能量积累后检测的THD检测器。理论分析表明THD检测器不需要散射中心分布的先验信息和目标运动的信息。分析了在高斯复噪声背景下，在没有目标回波信号时，用傅里叶变换计算的复高斯噪声互相关序列的概率密度分布，给出了恒虚警检测的门限。计算机仿真实验验证了理论分析的结果，比NSDD-GLRT检测器具有更好的检测能力。

［1］ Conte E， Antonio D M， and Ricci G. GLRT-based adaptive detection algorithms for range-spread targets［J］. IEEE Transactions on Signal Processing， 2001， 47（7）: 1336-1348.

［2］ Bon N， Khencharf A， and Garello R. GLRT subspace detection for range and Doppler distributed targets［J］. IEEE Transactions on Aerospace and Electronic Systems， 2008，44（2）: 678-696.

［3］ Jian Tao， He You， Su Feng， et al.. Cascaded detector for range-spread target in non-gaussian clutter［J］. IEEE Transactions on Aerospace and Electronic Systems， 2012，48（2）: 1713-1725.

［4］ 顾新锋， 简涛， 何友， 等. 局部均匀背景中距离扩展目标的GLRT检测器及性能分析［J］. 电子学报， 2013， 41（12）: 2367-2373. Gu Xin-feng， Jian Tao， He You， et al.. GLRT detector of range-spread target in local homogeneous background and its performance analysis［J］. Acta Electronica Sinica， 2013， 41（12）: 2367-2373.

［5］ 何友， 顾新锋， 简涛. 非高斯杂波背景中距离扩展目标的自适应积累检测器［J］. 中国科学: 信息科学， 2013， 43（4）: 488-501. He You， Gu Xin-feng， and Jian Tao. Adaptive integrator for range-spread target detection in non-gaussian clutter［J］. SCIENTIA SINICA Informationis， 2013， 43（4）: 488-501.

［6］ Dai Feng-zhou， Liu Hong-wei， Shui Peng-lang， et al.. Adaptive detection of w ideband radar range spread targets w ith range walking in clutter［J］. IEEE Transactions on Aerospace and Electronic System s， 2012， 48（3）: 2052-2064.

［7］ W ang P， Li H， Kavala T R， et al.. Generalized param etric rao test for multi-channel adap tive detection of range-spread targets［J］. IET Signal Processing， 2012， 6（5）: 404-412.

［8］ Shui Peng-lang， Xu Shu-wen， and Liu Hong-wei. Rangespread target detection using consecutive HRRPs［J］. IEEE Transactions on Aerospace and Electronic Systems， 2011，47（1）: 647-665.

［9］ Xu Shu-wen and Shui Peng-lang. Perform ance analysis of mu lti-channel order statistics detector for range-sp read target［J］. Journal of Systems Engineering and Electronics， 2012，23（5）: 689-699.

［10］ Xu Shu-wen and Shui Peng-lang. Range-spread target detection in wh ite Gaussian noise via two-dim ensional non-linear shrinkage map and geometric average integration［J］. IET Radar， Sonar & Navigation， 2012， 6（2）: 90-98.

［11］ Xu Shu-wen and Shui Peng-lang. Range-spread target detection in homogenous clutter via short-time GLRT estim ation and HOCC integration［C］. P roceed ings of the IET International Radar Conference 2013， Xi’an China， 2013: 1-6.

［12］ Carretero-M oya J， De M aio A， Gism ero-M enoyo J， et al.. Experimental performance analysis of distributed target coherent radar detectors［J］. IEEE Transactions on Aerospace and Electronic System s， 2012， 48（3）: 2216-2238.

［13］ 刘博， 常文革. 步进调频宽带雷达距离扩展目标频域检测算法［J］. 电子与信息学报， 2013， 35（10）: 2482-2486. Liu Bo and Chang Wen-ge. Range-sp read target detection of stepped chirp modulated radar in the frequency domain［J］. Journal of Electronics & Information Technology， 2013，35（10）: 2482-2486.

［14］ Zuo L， Li M， and Zhang X. CFAR detection of range-spread targets based on the time-frequency decom position feature of two ad jacent returned signals［J］. IEEE Transactions on Signal Processing， 2013， 61（4）: 6307-6319.

［15］ 赵宜楠， 庞晓宇， 王军， 等. 严重拖尾杂波中距离扩展目标的自适应极化检测［J］. 哈尔滨工业大学学报， 2014， 46（4）: 70-74. Zhao Yi-nan， Pang Xiao-yu， Wang Jun， et al.. Adaptive polarim etric detection of range spread targets in heavy-tailed com pound-Gaussian clutter［J］. Journal of Harbin Institute of Technology， 2014， 46（4）: 70-74.

［16］ 保铮， 邢梦道， 王彤， 等. 雷达成像技术［M］. 北京: 电子工业出版社， 2005: 20-45.

［17］ 吴顺君， 梅晓春. 雷达信号处理和数据处理技术［M］. 北京:电子工业出版社， 2008: 315-331.

［18］ 张贤达. 现代信号处理［M］. 第2版， 北京: 清华大学出版社，2002: 1-31.

［19］ Weisstein E W. Normal p roduct distribution［OL］. http: //mathworld.wolfram.com/NormalProductDistribution.htm l，Oct. 1999.

问 翔： 男，1977年生，博士生，研究方向为宽带雷达信号处理、雷达目标识别.

刘宏伟： 男，1971年生，博士，教授，博士生导师，研究方向为雷达信号处理、雷达目标识别、自适应信号处理.

包 敏： 男，1984年生，博士，讲师，研究方向为SAR/ISAR成像及动目标检测技术.

A Hough Transformation Detector for Range Spread Target

Wen X iang①Liu Hong-wei①Bao M in②①（National Laboratory of Radar Signal Processing， Xidian University， Xi’an 710071， China）
②（School of Electronic Engineering， Xidian University， Xi’an 710071， China）

For the issue that the range spread targets got from the w ideband radar signal are difficu lt to integrate for detect by the large velocity of target， a Hough Transformation Detector （HTD） is developed. Ad join high resolution radar range p rofiles of range spread target processes high correlation coefficient. Using this characteristic，signal energy integrated by Hough transformation in cross-correlation order and correlation time two dimensional plane and target detect are carried. Theory analysis show HTD is non-dependent on target scatter distribution in formation and target moving information and p rocesses Constant False A larm Ratio （CFAR） performance. Com puter sim ulation experim ent show HTD achieves better detection perform ance than Non-Scatterer Density Dependent Generalized Likelihood Ratio Test （NSDD-GLRT） detector.

Radar signal processing； Range spread target； Target detection； Constant False A larm Ratio （CFAR）；Hough transformation

TN957.51

： A

：1009-5896（2015）05-1104-07

10.11999/JEIT140692

2014-05-23收到，2015-01-13改回

国家自然科学基金（60901067， 61001212， 61201284）， 新世纪优秀人才支持计划（NCET-09-0630）及长江学者和创新团队发展计划（IRT0954）资助课题

*通信作者：刘宏伟 hw liu@xidian.edu.cn