基于瞬时频率估计的进动锥体目标微多普勒频率提取方法

曹文杰 张 磊 杜 兰刘宏伟

（西安电子科技大学雷达信号处理国家重点实验室 西安 710071）

基于瞬时频率估计的进动锥体目标微多普勒频率提取方法

曹文杰 张 磊 杜 兰*刘宏伟

（西安电子科技大学雷达信号处理国家重点实验室 西安 710071）

该文针对进动锥体目标的微动特性提取，建立等效散射点模型下的微多普勒频率与目标运动参数关系。结合进动调制的微多普勒频率近似正弦变化规律的特点，提出基于瞬时频率估计和随机抽样一致性（RANSAC）的进动目标微多普勒频率提取方法。该方法将回波信号分为若干段，每一段的回波信号近似为若干线性调频（LFM）信号分量之和，通过调频Relax算法估计各信号分量的瞬时频率，并通过随机抽样一致性算法估计散射点的微多普勒曲线。基于仿真数据和电磁计算数据的实验验证了该方法的有效性及稳健性。

目标识别；进动目标；微多普勒频率；线性调频信号；随机抽样一致性

1 引言

弹头等锥体目标在大气层外飞行时，为了保持姿态的稳定性，在绕自身对称轴自旋的同时还会绕空间某一定向轴进行锥旋，这种运动形式被称为进动。文献［1］最早将进动定义为微动的一种，并且将由微动产生的雷达回波的多普勒调制命名为微多普勒效应。由于微多普勒特性反映目标的电磁散射特性、几何结构和运动特性［2］，微多普勒特征已经成为弹道导弹目标分类识别的重要特征［35］-。而从雷达回波中准确提取微多普勒频率是微动参数估计和特征提取的关键，一些基于微多普勒的运动与结构参数估计方法也随之产生，如文献［6-8］。

现有的瞬时多普勒频率估计方法大致可以分为非参数化方法和参数化方法两类。非参数化方法不需要任何参数化模型或者参数化方程，一般首先计算信号的时频分布，然后通过跟踪时频分布图中的峰值来得到频率随时间的变化。文献［9］提出一种在时频分布（Time Frequency Distribution， TFD）的基础上，利用多目标跟踪（Multiple Target Tacking，M TT）技术分离空间锥体目标各等效散射中心微多普勒频率变化曲线的方法。针对TFD方法通常存在时频分辨率偏低和噪声敏感等不足，国内外学者提出了一系列基于参数化模型的瞬时多普勒频率估计方法。参数化方法需要利用信号的先验信息建立一个多参数模型来描述信号，然后利用数据对模型进行拟合估计模型参数。文献［10］利用时变自回归模型估计非平稳信号的瞬时多普勒频率，该方法首先用p阶时变自回归模型来表示信号分量的瞬时频率变化，利用回波数据拟合获得模型时变参数，然后根据信号功率谱密度极点位置实现对多信号分量的瞬时多普勒频率估计。实际应用中，参数化模型通常存在模型阶数选择以及参数耦合等问题，进动目标微动参数的估计是较为困难的。本文针对表面光滑的锥体目标，提出了一种基于瞬时频率估计的微多普勒频率提取方法，不直接对微动特性预先建模，而将回波分段后信号近似为若干散射点对应的线性调频信号分量的叠加，通过估计出各个线性调频信号的瞬时频率，然后利用随机抽样一致性进行模型拟合获得不同散射点的微多普勒频率曲线。

本文的结构如下：第2节建立了锥体目标的等效散射点模型，在此基础上对目标进动时各散射点瞬时微多普勒频率的变化情况进行了推导；第3节利用多分量线性调频信号对分段后的回波信号进行近似，用调频Relax算法对每一个线性调频信号分量的瞬时频率做参数估计，对估计出来的瞬时频率用随机抽样一致性算法进行区分，得到目标微多普勒频率的估计曲线。第4节采用仿真数据与电磁计算数据进行了仿真实验；实验结果验证了本方法的有效性和稳健性；第5节总结了全文。

2 锥体目标微多普勒分析

2.1 等效散射点模型

锥体目标的示意图如下，其中H为锥体目标高度，h为质心到底面的距离，r为底面圆半径，γ为半锥角，ϑ为雷达视线（radar Line O f Sight， rLOS）与锥体对称轴夹角。

对于无尾翼的光滑锥体目标，一般认为有3个散射点在起作用，分别是锥顶P3以及底部边缘上的两点P1， P2，其中P1， P2为雷达视线与目标对称轴所确定的平面与底面边缘的交点［11］。为区别一般散射点概念，称P1， P2为等效散射点，此时的目标模型为等效散射点模型。

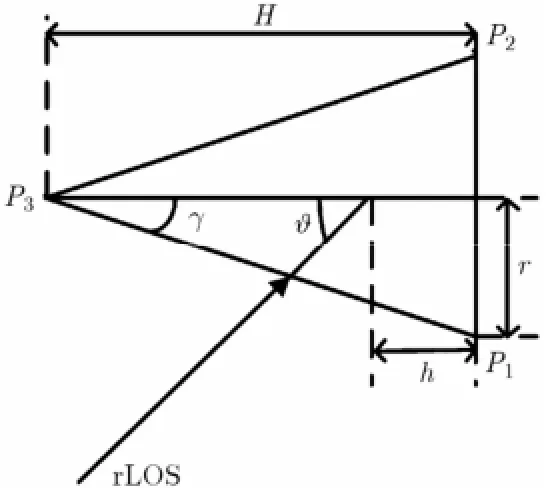
图1 锥体目标的示意图

在锥体目标飞行过程中，由于存在遮挡效应，使得一些散射点无法被雷达波照射到，散射点的遮挡效应由姿态角ϑ与锥体目标的半锥角γ共同决定。当ϑ从0到π变化时，P1， P2， P3的遮挡情况如表1所示。

表1 不同姿态角下各散射点遮挡情况

2.2 进动模型

建立目标进动模型如图2所示。以锥旋轴为Z轴建立参考坐标系OXYZ，其中O为锥体目标质心。雷达视线rLOS在YOZ平面内，与锥旋轴的夹角（平均视线角）为β；目标进动，除绕自身对称轴以角速度旋转外，还绕锥旋轴以角速度做锥旋运动，锥旋轴与目标对称轴的夹角为θ。在目标运动过程中建立新坐标系轴为锥体对称轴，Xn轴垂直于雷达视线与锥体对称轴所确定的平面，Yn轴由右手定则确定。设目标高度为H，质心距底面距离为h，底面圆半径为r，则3个散射点在新坐标系下的位置矢量分别为

雷达视线在参考坐标系OXYZ的单位矢量为：

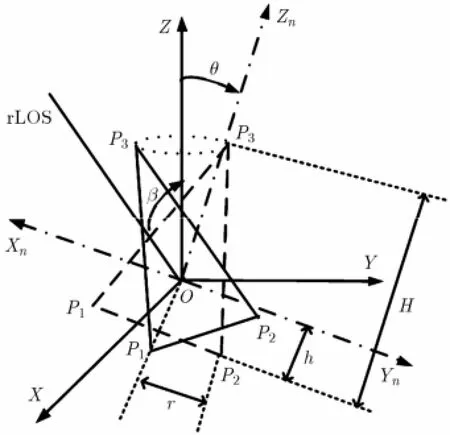
图2 进动模型

其中， M（t）表示目标的进动矩阵。由于光滑锥体目标为旋转对称体，因此其自旋运动并不影响电磁波的散射特性，本文中将忽略自旋运动而仅考虑锥旋运动。由文献［12，13］，可知锥旋旋转矩阵为

2.3 各散射点瞬时微多普勒频率变化分析

在任意时刻t，锥体目标对称轴方向与雷达视线夹角ε（t）的余弦为

由式（3）可得锥体目标对称轴方向与雷达视线夹角ε（t）的正弦为

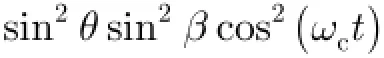
任意时刻t，散射点Pi在雷达视线上的投影可以表示为

散射点Pi的微多普勒频率为

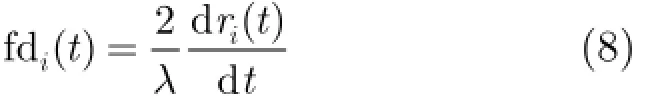
通过式（8）可得P1， P2和P33个散射点的瞬时微多普勒频率公式，其中λ为雷达波长。

3 微多普勒提取

由上节的理论推导可以看出，各散射点的瞬时微多普勒频率随时间是按正弦规律变化，但是在很短的时间内，可以认为瞬时多普勒频率随时间线性变化，如图3所示，图中的虚正弦曲线表示的是瞬时多普勒频率随时间呈现正弦规律变化，但是在较短的时间内，正弦曲线可以用图中的实直线来逼近。即可以把回波信号分为若干段，将每一段的回波信号近似为几个线性调频信号分量的叠加，通过估计这几个线性调频信号的瞬时频率这一参数，再对这些估计值进行区分，就可以得到目标的微多普勒频率。

对回波信号分段，一种可以采用均匀分段的方式，即每一段回波信号的数据长度相同；一种可以采用自适应分段的方式，开始选择比较大的数据个数，根据估计出来的每个线性调频信号分量的调频率、瞬时频率以及复幅度重构信号，计算重构误差，如果重构误差大于某一阈值，则减小数据个数，重复上面的过程，直到重构误差小于等于这一阈值，自适应分段可以认为是基于相同的重构误差对回波信号进行分段。与均匀分段的不同之处在于每一段回波信号的数据长度会有所不同，但是需要设置一个重构信号误差的阈值，使得重构误差小于这一阈值时结束数据长度的搜索，所需的计算量会比均匀分段大。

图3 一阶逼近示意图

3.1 线性调频信号参数估计

对于多分量线性调频信号的参数估计，文献［14，15］提出自适应chirplet分解的方法，文献［16，17］提出调频信号参数估计算法调频Relax。本文是通过调频Relax算法来估计每一段回波信号的各个线性调频信号分量的瞬时频率。

用M个线性调频信号分量的和对分段后的回波信号进行近似，可以表示为

其中，S（ t）表示分段后的回波信号，αi表示第i个线性调频信号分量的复幅度，f0i表示第i个线性调频信号分量的瞬时频率，mi表示第i个线性调频信号分量的调频率。

通过调频Relax算法，可以得到每一段回波信号的各个线性调频信号分量的复幅度、瞬时频率和调频率的估计值，本文只利用瞬时频率这个参数，把每一段观测时间的初始时刻作为横坐标，把估计出来的瞬时频率作为纵坐标，这样可以得到若干个离散的点，同一时刻的几个点表示的是这一时刻目标上可视散射点的瞬时微多普勒频率。

3.2 随机抽样一致性算法

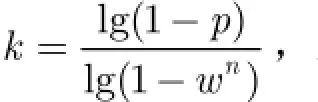
用随机抽样一致性算法对上节都得到的离散点进行区分，可以把这些点区分为局内点和局外点。

综上所述，本算法的流程为：

步骤1 初始化数据长度N，设置重构误差阈值E；

步骤 2 令N1=N，对前N1次回波做能量归一，并将其近似为M个线性调频信号的和，用调频Relax算法估计这M个线性调频信号分量的复幅度、瞬时频率和调频率；

步骤 3 根据步骤2得到的估计值去重构信号，计算与前N1次回波的重构误差，如果重构误差大于E，N1= N1- 1，转步骤2；否则，转步骤4；

步骤 4 记录此时N1的值和初始频率的M个估计值，并将回波信号的前N1次回波清除；再对清除之后的回波重复进行步骤2到步骤4操作，直到清除之后的回波信号的长度小于设置的初始化数据长度N；

步骤 5 将记录的N1和瞬时频率的估计值转换成一个两行的矩阵，第1行是由N1对应的时间，第2行是相应时间下瞬时频率的估计值，第1行表示横坐标，第2行表示纵坐标；

步骤 6 用随机抽样一致性算法对步骤5中矩阵表示的离散点进行区分，将其分为局内点以及局外点，分别由局内点和局外点分别估计正弦曲线的参数，得到目标的微多普勒频率曲线。

4 仿真实验

仿真参数设置：雷达发射窄带线性调频信号，载频10 GHz，带宽1 MHz，脉冲重复频率1 kHz，积累时间2 s，脉冲宽度10 μs。雷达视线rLOS与锥旋轴的夹角（平均视线角）为50°，锥旋频率2 Hz，进动角10°。锥体目标高度0.96 m，质心到底面的距离0.32 m，底面圆半径0.25 m。假设各散射点具有相同的散射强度。

电磁计算参数设置：雷达载频10 GHz，雷达视线俯仰角范围是0°∼ 90°（从锥顶开始是0°），采样间隔为0.02°，采用水平极化入射方式和水平极化接收方式。电磁计算方法采用的是物理光学（Physical Optics， PO）法。

4.1 仿真数据结果

对回波信号进行自适应分段，将每一段的回波信号近似为两个线性调频信号分量的和，用调频Relax算法估计每一段回波信号这两个线性调频信号的瞬时频率，估计结果如图4（a）所示，对图4（a）中的离散点用随机抽样一致性算法进行区分，可以把这些离散点区分为局内点以及局外点，以及由局内点和局外点分别确定的正弦曲线，结果如图4（b）所示。将瞬时多普勒频率的估计曲线以及由式（9）计算的理论曲线画在同一幅图中，结果如图5所示。

图4 估计的瞬时多普勒频率

图5 瞬时多普勒频率理论曲线与估计曲线的对比

从图5可以看出，瞬时多普勒频率的估计曲线与理论曲线基本重合，为了更加具体地描述估计结果，现引入式（11）来描述估计的正确率。

其中，IFe（k）表示瞬时多普勒频率的估计值，IFr（k）表示瞬时多普勒频率的理论值。

本文认为与点P3的瞬时多普勒频率理论曲线基本重合的曲线是其瞬时多普勒频率的估计曲线，与点P1的瞬时多普勒频率理论曲线基本重合的曲线是其瞬时多普勒频率的估计曲线，通过式（11）可以得到P3的瞬时多普勒频率的估计正确率为97.51%， P1的瞬时多普勒频率的估计正确率为97.51%。

其他条件不变，在回波信号中加入不同信噪比的高斯白噪声，仍然用自适应的方式对回波信号进行分段。不同信噪比情况下，P3和P1的瞬时多普勒频率的估计正确率如图6中实线所示，多目标跟踪方法得到的正确率如图中虚线所示。

从图6可以看出，用本文所提方法能得到比较高的估计正确率。

4.2 电磁计算数据结果

对电磁计算的回波数据，采用均匀分段的方式对其进行分段，其他过程与4.1节的实验过程相同，不同信噪比情况下，P3和P1的瞬时多普勒频率的估计正确率为如表2所示。

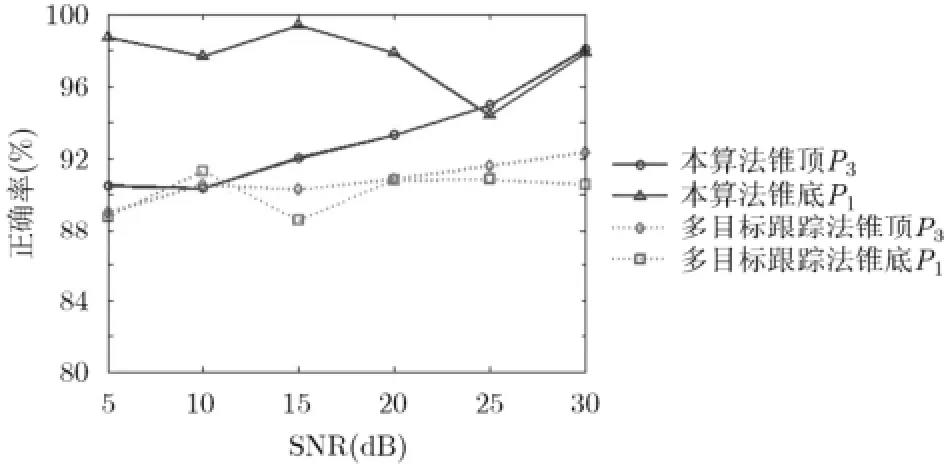
图6 本文所提方法与多目标跟踪方法的正确率的对比图

从表2可以看出，噪声对估计正确率的影响不大。

由实验结果可以看出，本文所提的方法能得到比较高的正确率并且对噪声有一定的稳健性。

5 结束语

本文分析了锥体目标进动时的微多普勒频率，对于微多普勒频率呈现正弦规律变化的形式，本文提出基于瞬时频率估计的微多普勒频率提取方法，该方法首先将回波信号分为若干段，将每一段的回波信号近似为几个线性调频信号分量的和，用调频Relax算法估计每一个线性调频信号分量的瞬时频率，再用随机抽样一致性算法区分这些估计值，最终得到目标微多普勒频率的估计曲线。实验结果表明，本文提出的基于瞬时频率估计的微多普勒频率提取方法可以有效地提取锥体目标各等效散射点的微多普勒频率。如何利用提取的微多普勒频率进行目标识别将是下一步的研究方向。

表2 不同信噪比情况下的估计正确率（%）

参 考 文 献

［1］ Chen V C， Li F， and Wechsler H. M icro-Doppler effect in radar phenomenon， model and simulation study［J］. IEEE Transactions on Aerospace and Electron ic System， 2006， 42（1）: 2-21.

［2］ 周万幸. 弹道导弹雷达目标识别技术［M］. 北京: 电子工业出版社， 2011: 1-19.

［3］ 韩勋， 杜兰， 刘宏伟， 等. 基于时频分布的空间锥体目标微动形式分类［J］. 系统工程与电子技术， 2013， 35（4）: 684-691. Han Xun， Du Lan， Liu Hong-wei， et al.. C lassification of m icro-motion form of space cone-shaped ob jects based on time-frequency distribution［J］. Systems Engineering and Electronics， 2013， 35（4）: 684-691.

［4］ 贾守卿， 江小敏， 夏明耀. 基于微多普勒特征的目标分类［J］.电波科学学报， 2013， 28（3）: 443-447. Jia Shou-qing， Jiang X iao-m in， and Xia M ing-yao. Target classification by m icro-Doppler feature［J］. Chinese Journal of Radio Science， 2013， 28（3）: 443-447.

［5］ 关永胜， 左群声， 刘宏伟. 基于微多普勒特征的空间锥体目标识别［J］. 电波科学学报， 2011， 26（2）: 209-215. Guan Yong-sheng， Zuo Qun-sheng， and Liu Hong-wei. M icro-Dopp ler signatu re based cone-shaped target recognition［J］. Chinese Journal of Radio Science， 2011， 26（2）: 209-215.

［6］ 邹小海， 艾晓峰， 李永祯， 等. 基于微多普勒的圆锥弹头进动与结构参数估计［J］. 电子与信息学报， 2011， 33（10）: 2413-2419. Zou X iao-hai， A i Xiao-feng ， Li Yong-zhen， et al.. P recession and structure parameter estimation of the cone-shaped warhead based on the m icro-Doppler［J］. Journal of Electronics & Inform ation Technology， 2011， 33（10）: 2413-2419.

［7］ 李飞， 纠博， 邵长宇， 等. 目标微动参数估计的曲线跟踪算法［J］. 电波科学学报， 2013， 28（2）: 278-284. Li Fei， Jiu Bo， Shao Chang-yu， et al.. Curve tracking based parameter estimation of micro-motion［J］. Chinese Journal of Radio Science， 2013， 28（2）: 278-284.

［8］ 王兆云， 张兴敢， 柏业超. 基于微多普勒的锥体目标进动和结构参数估计［J］. 南京大学学报（自然科学）， 2014， 50（2）: 148-153. Wang Zhao-yun， Zhang Xing-gan， and Bai Ye-chao. Precession and structural parameter estimation of cone-shaped target based on the m icro-Dopp ler［J］. Journal of Nanjing University （Natural Sciences）， 2014， 50（2）: 148-153.

［9］ 邵长宇， 杜兰， 李飞， 等. 基于多目标跟踪的空间锥体目标微多普勒频率提取方法［J］. 电子与信息学报， 2012， 34（12）: 2972-2977. Shao Chang-yu， Du Lan， Li Fei， et al.. M icro-Doppler extraction from space cone target based on m ultip le target tracking［J］. Journal of Electronics & Information Technology，2012， 34（12）: 2972-2977.

［10］ Sharm an K C and Fried lander B. T im e-varying autoregressive modeling of a class of non-stationary signals［C］. Proceedings of IEEE International Conference on Acoustics，Speech， and Signal Processing， Glasgow， Scotland， 1984: 227-230.

［11］ 黄培康， 殷红成， 许小剑. 雷达目标特性［M］. 北京: 电子工业出版社， 2005: 229-234.

［12］ Gao Hong-wei， Xie Liang-gui， W en Shu-liang， et al.. M icro-Dopp ler signature extraction from ballistic target w ith m icro-Motions［J］. IEEE Transactions on Aerospace and Electronic System s， 2010， 46（4）: 1969-1982.

［13］ 喻荣梅， 张仕元， 肖健华. 弹道目标移动散射点模型的微多普勒特征研究［J］. 测控技术， 2014， 33（3）: 154-156. Yu Rong-mei， Zhang Shi-yuan， and Xiao Jian-hua. Research on m icro-Doppler signature of ballistic target based on moving scattering center model［J］. Measurement & Control Technology， 2014， 33（3）: 154-156.

［14］ 邹虹， 保铮. 一种有效的基于chirplet自适应信号分解算法［J］.电子学报， 2001， 29（4）: 515-517. Zou Hong and Bao Zheng. An efficient algorithm for adaptive chirplet-based signal decomposition［J］. Acta Electronica Sinica， 2001， 29（4）: 515-517.

［15］ 蔡洪， 何强， 赵春宇. 基于自适应Chirplet分解的非均匀转动目标ISAR相位聚焦［J］. 电光与控制， 2013， 20（6）: 79-84. Cai Hong， He Qiang， and Zhao Chun-yu. ISAR phase focusing for nonuniform rotating target based on adaptive chirplet decom position［J］. E lectron ics Optics & Con tro l， 2013，20（6）: 79-84.

［16］ 张群， 马长征， 张守宏. 机动目标三维成像中调频信号超分辨方法［J］. 应用科学学报， 2000， 18（2）: 114-116. Zhang Qun， M a Chang-zheng， and Zhang Shou-hong. Superresolution of chirp signals and its applications to three dimensional imaging of maneuvering Targets［J］. Journal of Applied Sciences， 2000， 18（2）: 114-116.

［17］ 邢孟道， 保铮， 冯大政. 基于调幅-线性调频信号参数估计的机动目标成像方法［J］. 现代雷达， 2006， 12（6）: 44-49. Xing M eng-dao， Bao Zheng， and Fen Da-zheng. Dynam ic ISAR imaging of maneuvering target based on muticom ponent AM-LFM signal parameter estimation［J］. M odern Radar， 2006， 12（6）: 44-49.

［18］ M artin Fischler and Robert Bolles. Random sam p le consensus: a paradigm for m odel fitting w ith app lications to image analysis and autom ated cartography［J］. Communications of the ACM， 1981， 24（6）: 381-395.

曹文杰： 男，1987年生，博士，研究方向为雷达空间目标识别.

张 磊： 男，1984年生，博士，讲师，研究方向为SAR、ISAR高分辨成像与运动补偿.

杜 兰： 女，1980年生，博士，教授，博士生导师，研究方向为统计信号处理、雷达信号处理、机器学习及其在雷达目标检测与识别方面的应用.

刘宏伟： 男，1973年生，博士，教授，博士生导师，研究方向为雷达信号处理、M IMO雷达、雷达目标识别、自适应信号处理、认知雷达等.

M icro-Dopp ler Frequency Extraction for Cone-shaped Target w ith Precession Based on Instantaneous Frequency Estimation

Cao Wen-jie Zhang Lei Du Lan Liu Hong-wei
（National Lab of Radar Signal Processing， Xidian University， Xi’an 710071， China）

Based on the equivalent scatter point model， the relationship between the m icro-Dopp ler frequencies and the motion parameters of the cone-shaped target w ith p recession is estab lished. Due to the approximately sinusoidal form of the m icro-Dopp ler frequency m odu lation induced by the p recession， an app roach to extract the m icro-Dopp ler frequency of the target with p recession based on the instantaneous frequency estimation and the RANdom SAm p le Consensus （RANSAC） is p roposed. In this method， the target echo signal is first divided into several segments. Then each segment of the echo signal app roximates to the sum of several components of the Linear Frequency Modu lation （LFM） signal， and an algorithm based on the extended Relax method is used to estimate the instantaneous frequency of the each LFM signal. Thus the m icro-Doppler curve of each equivalent scatter point is estimated by the RANSAC algorithm. In the simu lation experim ents， the perform ance of the proposed method is evaluated via the simulation data and electromagnetic com putation simulation data.

Target recognition； Target with p recession； M icro-Dopp ler frequency； Linear Frequency Modulation（LFM） signal； RANdom SAm ple Consensus （RANSAC）

TN957.51

： A

：1009-5896（2015）05-1091-06

10.11999/JEIT140985

2014-07-23收到，2014-12-09改回

国家自然科学基金（61271024， 61322103， 61301280）和全国优秀博士学位论文作者专项资金（FANEDD-201156）资助课题

*通信作者：杜兰 dulan@mail.xidian.edu.cn