分析问题的三种方法

赵文龙

学生面对新题时，因为陌生，往往不知如何入手，平时所学知识、思想、方法无法使用，所以就认为题目“难”，无法解答.出现这种现象的原因是不会分析问题，也就是不能正确选择解题方法.下面以2013年安徽省高考数学题为例，介绍分析问题的三种方法，从而帮助学生提高分析问题和解决问题的能力.

1.联想法

有的题目表面上是以一块知识呈现，但要解决问题则需要另一块知识，能否将知识顺利切换是关键.联想法解题策略就是根据题目有关特征，联想到相关知识，应用相关知识解决问题.

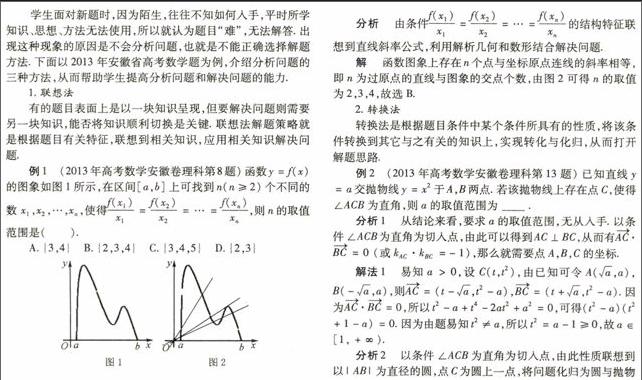
例1 （2013年高考数学安徽卷理科第8题）函数y=f（x）的图象如图1所示，在区间[a，b]上可找到n（n≥2）个不同的数 x1，x2，…，xn，使得f（x1）x1=f（x2）x2=…=f（xn）xn，则n的取值范围是（ ）.

A.{3，4} B.{2，3，4} C.{3，4，5} D.{2，3}

分析 由条件f（x1）x1=f（x2）x2=…=f（xn）xn的结构特征联想到直线斜率公式，利用解析几何和数形结合解决问题.

解 函数图象上存在n个点与坐标原点连线的斜率相等，即n为过原点的直线与图象的交点个数，由图2可得n的取值为2，3，4，故选B.

2.转换法

转换法是根据题目条件中某个条件所具有的性质，将该条件转换到其它与之有关的知识上，实现转化与化归，从而打开解题思路.

例2 （2013年高考数学安徽卷理科第13题）已知直线y=a交抛物线y=x2于A，B两点.若该抛物线上存在点C，使得 ∠ACB为直角，则a的取值范围为 ______ .

分析1 从结论来看，要求a的取值范围，无从入手.以条件∠ACB为直角为切入点，由此可以得到AC⊥BC，从而有

AC·BC=0 （或kAC·kBC=-1），那么就需要点A，B，C的坐标.

解法1 易知a>0，设C（t，t2），由已知可令A（a，a），B（-a，a），则AC=（t-a，t2-a），BC=（t+a，t2-a）.因为AC·BC=0，所以t2-a+t4-2at2+a2=0，可得（t2-a）（t2+1-a）=0.因为由题易知t2≠a，所以t2=a-1≥0，故a∈[1，+∞）.

分析2 以条件∠ACB为直角为切入点，由此性质联想到以|AB|为直径的圆，点C为圆上一点，将问题化归为圆与抛物线相交.

解法2 设直线y=a与y轴交于点M，抛物线y=x2上要存在C点，只要以|AB|为直径的圆与抛物线y=x2有交点即可，也就是使|AM|≤|MO|，即a≤a（a>0），故a∈[1，+∞）.

3.逆推法

结论就是解一道题最终获得的答案，有时它对解题目标或解题方向有暗示作用，利用好结论的隐含信息及所学知识，从结论出发，做逆向分析探究，可以顺利求解问题.

例3 （2013年高考数学安徽卷理科第14题）如图3，互不相同的点A1，A2，…，An，…和B1，B2，…，Bn，…分别在角O的两条边上，所有AnBn相互平行，且所有梯形AnBnBn+1An+1的面积均相等.设OAn=an.若a1=1，a2=2，则数列{an}的通项公式是 ______.

分析 从题目要求结论和所提供的

条件特点可知，若要求数列{an}的通项公式，则需要求出数列{an}的递推公式（利用数列递推公式求通项公式是常用的方法），以梯形 AnBnBn+1An+1面积均相等为切入点，求出数列{an}的递推公式.

解 设AnBn=cn，△OAnBn边AnBn上高为hn，因为所有AnBn相互平行，且OAn=an，所以an-1an=cn-1cn=hn-1hn，则cn-1=an-1ancn，hn-1=an-1anhn，同理cn+1=an+1ancn，hn+1=an-1anhn.梯形An-1Bn-1BnAn的面积为12（cn-1+cn）（hn-hn-1）=12（an-1ancn+cn）（hn-an-1anhn），梯形AnBnBn+1An+1的面积为12（cn+cn+1）（hn+1-hn）=12（cn+an-1ancn）（

an-1anhn-hn）.由两梯形的面积相等可得

12（an-1ancn+cn）（hn-an-1anhn）=12（cn+an+1ancn）（an+1anhn-hn），1-a2n-1a2n=a2n+1a2n-1，

2a2n=a2n-1+a2n+1.所以数列{a2n}是首项为a21=1，公差为a22-a21=22-1=3的等差数列，所以a2n=1+（n-1）×3=3n-2（an>2），所以an=3n-2.