传导冷却高温超导磁体热输运参数反演识别*
李 想,汤智胤,吴 钢,周 刚,毕 柯,张青枝
(1.海军工程大学 动力工程学院, 湖北 武汉 430033; 2.中国科学院 低温工程学重点实验室, 北京 100190)
传导冷却高温超导磁体热输运参数反演识别*
李想1,汤智胤1,吴钢1,周刚2,毕柯1,张青枝1
(1.海军工程大学 动力工程学院, 湖北 武汉430033; 2.中国科学院 低温工程学重点实验室, 北京100190)
摘要:在传导冷却高温超导磁体系统中,超导磁饼热导率以及磁饼与导冷体之间的界面热阻是影响热输运的主要因素,也是传导冷却超导磁体系统热设计的难点。为了获得准确的热导率和界面热阻参数,根据 Levenberg-Marquardt算法提出通过表面测温确定传导冷却超导磁体热输运参数的反演识别方法。搭建低温实验数据测试平台,建立高温超导磁饼三维各向异性热传导模型。利用反演算法对传导冷却Bi2223高温超导磁体在40~76K温区的各向异性热导率与界面热阻进行反演识别,并分析测温误差对识别结果的影响。研究成果将为超导磁体热输运参数的获取提供一种新思路。
关键词:高温超导;热导率;界面热阻;各向异性;参数识别
近些年来,低温制冷技术和新型高温超导材料的发展,极大地推动了超导磁体的应用[1]。相比于液体浸泡冷却超导磁体,传导冷却超导磁体可以获得更宽的运行温度,而且结构紧凑、运行维护方便、安全性好,是超导磁体应用研究的重要方向[2]。传导冷却高温超导磁体热输运参数(主要包括超导磁饼各向热导率以及超导磁饼与导冷结构之间的界面热阻)对传导冷却高温超导磁体的热设计和热分析至关重要。
目前,超导磁饼热导率主要采用以下几种方法获取:一是采用超导带材的热导率作为磁饼的热导率[3];二是按照超导磁饼中各种材料组分比进行热导率参数的换算[4];三是采用传统的热导率测试方法,从磁饼上切割标准样品进行测试[5-6]。然而磁饼是由高温超导(High Temperature Superconducting,HTS)带材缠绕而成,并经过绝缘处理、环氧树脂浸渍固化,其热物性参数与带材有较大不同,具有强烈的各向异性;第二种方法忽略不同组分材料之间的界面热阻与组织结构;第三种方法准确性最高,但从磁饼上切割样品进行测试将会导致整个磁饼的报废,代价太大。目前对于HTS磁体系统中的界面热阻也有一定的研究[7-9],但这些大都是基于单一材质之间或者单一材质与超导带材之间的界面热阻研究,而实际传导冷却超导磁体系统热分析中所涉及的界面热阻主要体现在具有一定结构特征的超导磁饼与导冷结构之间。
当前,国内外不仅缺乏完整的传导冷却超导磁体热输运参数数据,而且也缺乏有效的获取方法。为此,提出了基于导热反问题的方法对传导冷却超导磁体热输运参数进行反演识别。
1低温实验设计
通过反演的方法获取HTS磁饼各向异性热导率,首先需要根据被研究对象结构特征设置合适的边界条件,使其内部的热物性特征通过外在的温度场分布体现出来。要实现HTS磁饼径向、轴向、周向热导率的准确识别,必须在这3个方向上形成明显的温度梯度。为此,对HTS磁饼的传热边界条件设定如图1所示,通过加热器对超导磁饼上的区域Ω1施加均匀热流;区域Ω2与导冷体的控温面接触。导冷体与磁饼之间的界面热阻通过导冷体控温面与磁饼接触面之间的温差体现出来。

图1 边界条件设置Fig.1 Settings of boundary
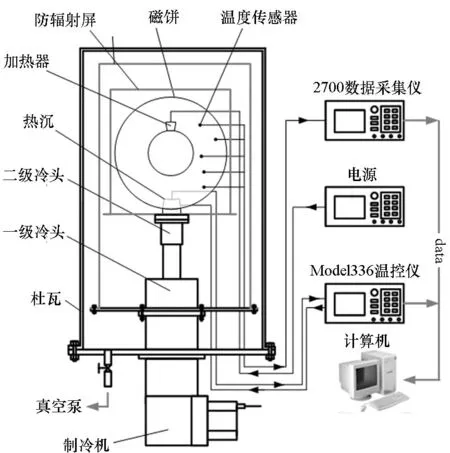
图2 低温实验系统Fig.2 Low temperature experiment system
为了实现上述边界条件,建立了如图2所示的低温实验系统。该实验系统主要包括低温测量单元、低温温控单元、真空单元[10]。低温温控单元由低温制冷机、温控仪、加热器、温度传感器组成。冷量主要由制冷机二级冷头提供,并在一级冷头和二级冷头上安装防辐射屏,减少辐射热对样品的影响,控温过程中由温度传感器感受导冷体控温面温度变化并反馈给温控仪,温控仪通过调节加热器电流大小来控制加热量,从而使控温面温度达到设定值。真空单元由真空泵、复合真空计等组成,用来提供和监测真空测试环境。
2导热正问题模型与数值求解
2.1 三维各向异性热传导模型
HTS磁饼截面如图3所示,r0,r1分别为HTS磁体的内、外径;L0为HTS磁体的厚度;Ω为磁饼所有的边界集合。HTS磁饼热导率在轴向、径向和周向是正交异性的,柱坐标系下三维正交异性稳态热传导微分方程为:
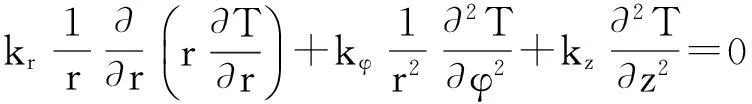
(1)
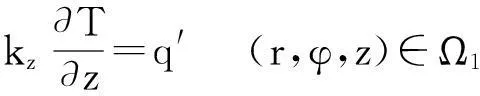
(2)
T(r,φ,z)=Tb-RCq(r,φ,z)∈Ω2
(3)
其他边界面为绝热,满足
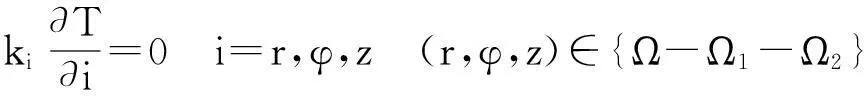
(4)
其中:T为HTS磁饼的温度分布;r,z,φ分别为径向、轴向和周向坐标;kr,kz,kφ分别为HTS磁饼径向、轴向和周向的热导率;Tb为导冷体控温面温度;q′为磁饼边界热流密度。稳态时由区域Ω1进入磁饼的热流等于由区域Ω2流出磁饼的热流。如图4所示,由于界面热阻的存在,磁饼温度边界区域Ω2处的实际温度边界应为Tb-RCq,RC为磁饼与导冷体之间的界面热阻,q为流经接触界面处的热流密度。

图3 HTS磁饼截面图Fig. 3 Sectional view of HTS magnetic pancake
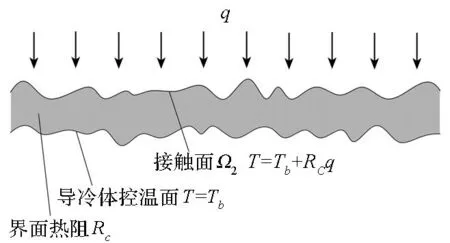
图4 界面热阻Fig.4 Thermal boundary resistance
2.2 正问题求解
三维正交异性热传导正问题求解通常很难获得解析解,可以通过数值方法进行求解。有限体积法是在有限差分法的基础上发展起来的,同时吸收了有限元法的一些优点,具有物理意义明确、计算精度高等特点。采用有限体积法三维均匀网格系统来离散求解域,柱状体三维控制容积如图5所示。节点P位于控制容积的中部,它有6个相邻节点,分别位于东(点E)、西(点W)、南(点S)、北(点N)、上(点A)、下(点B)方向。e,w,s,n,t,b分别代表控制体的东侧、西侧、南侧、北侧、上侧、下侧边界。
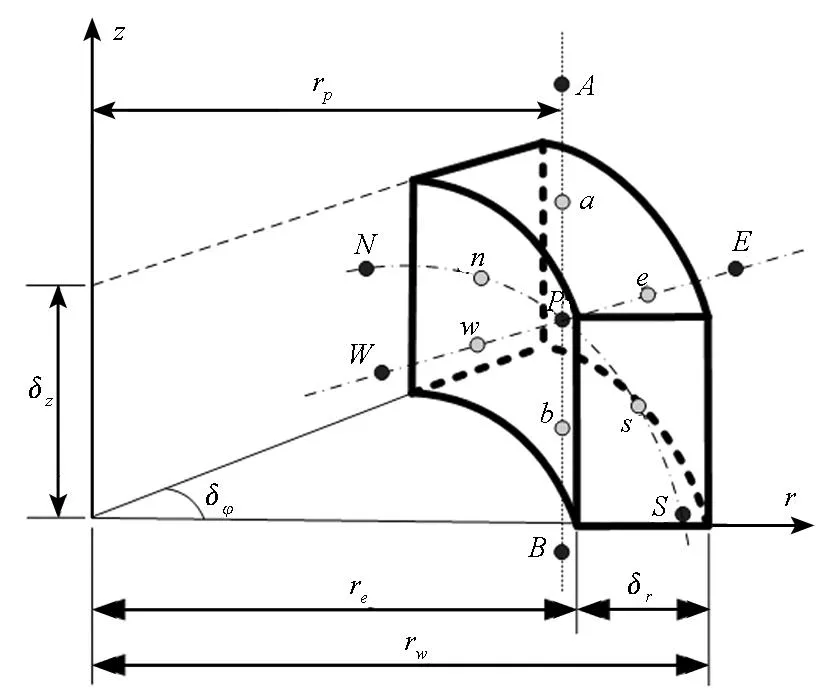
图5 单元体极坐标Fig.5 Unit under polar coordinates
有限体积法通过对控制体积的积分来实现方程的离散,在控制容积内对式(1)进行积分,则得到节点P对应的离散方程:
aPTP=aETE+aWTW+aNTN+aSTS+aATA+aBTB+Su
(5)
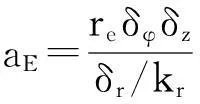
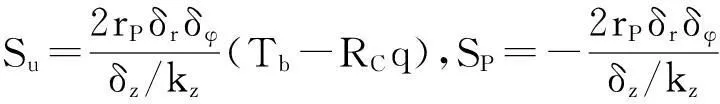
3导热反问题热输运参数识别
3.1 导热反问题参数识别描述
导热反问题热输运参数反演识别的本质是通过对待识别热输运参数初始假设按照一定算法不断修正,并代入正问题求解模型获得相应温度分布,以期找到一组热输运参数使检测点的求解温度分布与其真实温度分布相吻合。检测点的求解温度与实际测试温度的吻合程度可以采用目标函数S(P)来衡量。
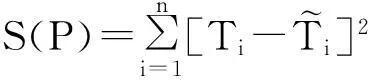
(6)

3.2 Levenberg-Marquardt反问题算法
Levenberg-Marquardt算法是一种简单、收敛速度快的优化算法[12]。它通过使目标函数最小化来确定反问题的解。通过对式(6)求偏导可得到S(P)最小化条件:
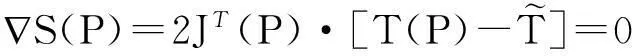
(7)
其中,J(P)=∂T(P)/∂PT。将T(P)在Pk处按泰勒级数展开并去掉高阶项,同时在结果中加入衰减参数μ调节收敛速度,得到P的迭代公式:

(8)
其中:上标k表示迭代次数,Pk是第k次迭代得到的识别参数向量,T(Pk)、Jk分别是在参数向量Pk下计算得到的检测面温度和敏感系数矩阵;μ为一个取正值的调节系数,W为一对角矩阵。
4实例与结果分析
采用Bi2223高温超导磁饼为研究对象,图6为其实物结构,其外径r1=135mm,内径r0=75mm,厚度h=10mm。根据磁饼的结构设置磁饼的热边界条件如图7所示,扇形区域Ω1为热流边界,扇形区域Ω2为恒定的温度边界。

图6 Bi2223高温超导磁饼Fig.6 HTS Bi2223 pancake coils
在HTS磁体上依次设置4个热电偶监测温度,设置位置如图7所示。采用紫铜作为导冷体与超导磁饼上区域Ω2接触,并在两界面之间填充低温导热脂。导冷体的温度控制在Tb=40K,磁饼上区域Ω1的热流密度为q=5000W/m2。
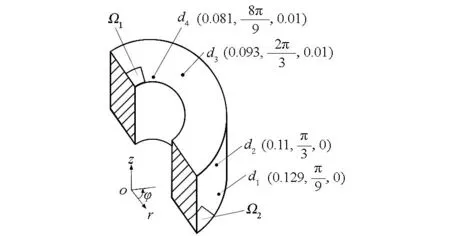
图7 测温点设置Fig.7 Setting of temperature measuring points
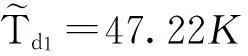
图8中反演识别结果显示Bi2223超导磁饼轴向、周向和径向的热导率分别为kz=4.07W·m-1K-1,kφ=225.46W·m-1K-1,kr=0.538W·m-1K-1;导冷体与磁饼之间的界面热阻为Rc=1.74×10-3m2K·W-1。由图9可知,Levenberg-Marquardt算法在热传导反问题热输运参数识别中具有较高的精度和较快的收敛速度。为了考虑测温误差对反演识别结果的影响,假设温度测量误差服从正态分布,TP=(1+σ·ξ)Te为含有测量误差的测点温度信息,Te为测点温度信息的真实值,σ为系统测温误差水平,ξ为服从正态分布的随机变量。表1为不同测温误差水平下热输运参数的定量识别结果,当测温误差小于0.3K时,热导率的识别误差小于16.1%。

图8 热输运参数辨识过程Fig.8 Process of heat transfer parameter identification
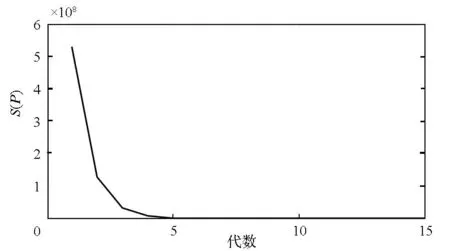
图9 收敛精度Fig.9 Convergence precision
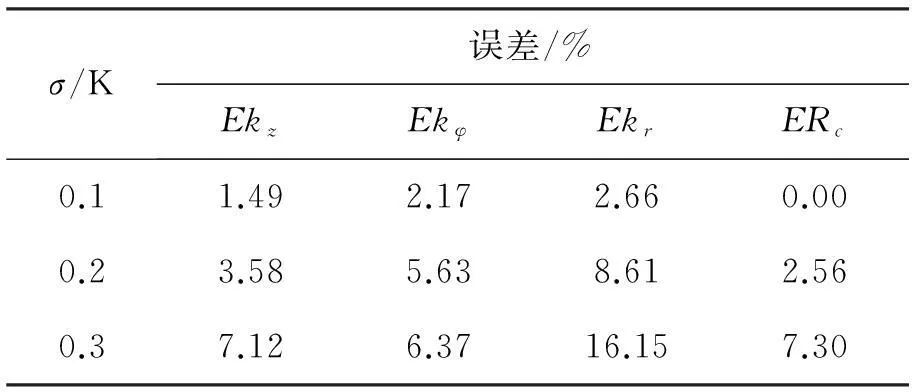
表1 测温误差对识别结果的影响
5结论
1)根据HTS磁体的结构特征,提出了通过反问题算法与低温实验相结合手段,同时确定传导冷却超导磁体中磁饼各向异性热导率以及超导磁饼与导冷体之间界面热阻的方法。
2)通过该方法获得了高温超导Bi2223磁饼在工作温区轴向、径向和周向热导率以及磁饼与Cu导冷体之间界面热阻数据,能够为传导冷却高温超导磁饼的热分析和热设计提供参考。
3)反演识别结果表明经过环氧树脂固化的Bi2223高温超导磁饼具有严重的各向异性:磁饼周向热导率比轴向热导率高2个数量级,比径向热导率高3个数量级。因此,采用文献[3-6]中简单方法确定的磁饼的热导率是很难满足磁体精确化热设计需求的。
4)低温下导冷体与磁饼之间存在较大的界面热阻,在传导冷却超导磁体的热设计过程中不容忽视。
5)采用Levenberg-Marquardt算法对传导冷却高温超导磁体热输运参数进行反演识别,具有收敛速度快,收敛精度高等优点。
参考文献(References)
[1]Ono M, Kuriyama T, Oguchi A, et al. Cryocooler-cooled highTcsuperconducting magnet excited by thermoelectromotive force[J]. IEEE Transactions on Applied Superconductivity, 2004, 14(2): 1194-1197.
[2]Choi Y S, Kim D L, Shin D W. Initial cooldown characteristic of conduction-cooled high field magnet system[J]. IEEE Transactions on Applied Superconductivity, 2011, 21(3): 1604-1607.
[3]唐斯密,吴钢,王惠龄,等.直接冷却的高温超导磁体热稳定性有限元仿真[J].低温与超导,2006,34(6):446-450.
TANG Simi, WU Gang, WANG Huiling, et al. Simulation on the thermal stability of the superconducting magnet directly cooled by cryocooler based on FEM[J].Cryogenics and Superconductivity, 2006,34(6):446-450.(in Chinese)
[4]Lehtonen J, Mikkonen R, Paasi J. Effective thermal conductivity in HTS coils [J]. Cryogenics, 2000, 40(4): 245-249.
[5]Huang T T, Johnstone A, Yang Y F, et al. Finite element modeling of thermal stability and quench propagation in a pancake coil of PbBi2223 tapes [J].IEEE Transactions on Applied Superconductivity, 2005, 15 (2): 1647-1650.
[6]Naitoa T,Fujishiro H,Yamada Y.Anisotropic thermal transport in double-pancake coil wound with DI-BSCCO tape[J].Physica C: Superconductivity,2010, 470(20):1397-1400.
[7]Bi D M, Chen H X, Tian Y. Influences of temperature and contact pressure on thermal contact resistance at interfaces at cryogenic temperatures[J]. Cryogenics, 2012, 52(7): 403-409.
[8]Rao R S, Wang J R, Zhuang H R, et al. An investigation on interface thermal resistance at superconductor cooling by cryocooler[J]. Physica C: Superconductivity, 2003, 386(8): 547-550.
[9]Fujishiro H,Okamoto T,Hirose K.Thermal contact resistance between high-Tcsuperconductor and copper[J].Physica C: Superconductivity,2001,357(8): 785-788.
[10]王惠龄. 超导应用低温技术[M].北京:国防工业出版社,2008.
WANG Huiling. Superconducting application low temperature technology [M]. Beijing: National Defense Industry Press, 2008. (in Chinese)
[11]李人宪.有限体积法基础[M]. 2版.北京:国防工业出版社,2008.
LI Renxian. The foundation of finite volume method[M]. 2rd ed. Beijing: National Defense Industry Press, 2008. (in Chinese)
[12]Marquardt D W. An algorithm for least-squares estimation of nonlinear parameters[J]. Journal of the Society for Industrial and Applied Mathematics, 1963, 11(2): 431-441.
http://journal.nudt.edu.cn
Inversion identification of heat transport parameters of conduction cooling high temperature superconducting magnet
LIXiang1,TANGZhiyin1,WUGang1,ZHOUGang2,BIKe1,ZHANGQingzhi1
(1. College of Power Engineering, Naval University of Engineering, Wuhan 430033, China;
2. Key Laboratory of Cryogenics, Chinese Academy of Sciences, Beijing 100190, China)
Abstract:In conduction cooling high temperature superconducting (HTS) magnet system, thermal conductivity of HTS magnetic pancakes and thermal boundary resistance between magnetic pancake and cooling body are the major factors affecting heat transport, and the difficult points for the thermal design of conduction cooling HTS magnet as well. A new method, based on the Levenberg-Marquardt algorithm, to simultaneously identify each heat transport parameter from the temperature distribution on the inspection surface was put forward. A low temperature experiment platform was setup, and a three-dimensional orthotropic heat transfer model of magnetic pancake was built. The orthotropic thermal conductivity and thermal boundary resistance of conduction cooling Bi2223 HTS magnet at 45~72 K were obtained with the method mentioned above. The influence of temperature measurement error on identification results was analyzed. The research result provides a new thought for obtaining heat transport parameters of conduction cooling superconducting magnet.
Key words:high temperature superconducting; thermal conductivity; thermal boundary resistance; orthotropic; parameter identification
中图分类号:O511.2
文献标志码:A
文章编号:1001-2486(2015)06-150-05
作者简介:李想(1986—),男,河南信阳人,博士研究生,E-mail:suplixiang@163.com; 吴钢(通信作者),男,教授,博士,博士生导师,E-mail:gangwu206@hotmail.com
基金项目:国家自然科学基金资助项目(51076165);中国科学院重点实验室基金资助项目(CRYO201221)
收稿日期:*2014-12-23
doi:10.11887/j.cn.201506027

