黏弹性基底上阻尼碳纳米管的动力学特性*
张大鹏,雷勇军
(国防科技大学 航天科学与工程学院, 湖南 长沙 410073)
黏弹性基底上阻尼碳纳米管的动力学特性*
张大鹏,雷勇军
(国防科技大学 航天科学与工程学院, 湖南 长沙410073)
摘要:采用欧拉梁模型建立了有阻尼碳纳米管在黏弹性基底上的动力学问题分析模型。通过引入非局部理论、广义Maxwell黏弹性模型、速度相依的外阻尼模型及黏弹性基底模型推导出碳纳米管动力学分析的欧拉梁振动控制方程。在Kelvin-Voigt黏弹性模型基础上,分别给出无基底和全基底支撑时碳纳米管固有频率的一般解析表达式,并分析讨论全基底时的多种典型情况。然后利用传递函数方法求解出一般边界条件下振动控制方程的封闭解。以某单壁碳纳米管为例,得到不同边界条件下该单壁碳纳米管的前四阶固有频率,并分析了碳纳米管非局部参数、黏弹性参数、基底刚度及长度等影响因素对固有频率和阻尼因子的影响情况。结果表明,文中所建的动力学分析模型及计算方法对解决碳纳米管在黏弹性基底上的动力学问题准确有效。
关键词:动力学特性;黏弹性基底;欧拉梁;非局部弹性理论;传递函数方法
自1991年被发现以来[1],碳纳米管(Carbon Nanotubes, CNT)以优异的力学、化学、电学及光学性能在物理、化学、纳米工程、电子工程和材料工程等领域得到广泛应用[2-5]。为指导工程实践,相关学者在碳纳米管制备[6]、电学[7-8]、力学[9-13]等方面进行了大量研究。在力学试验方面,近年来曼彻斯特大学的Young[14-16]通过将碳纳米管或石墨烯固定在有机玻璃上,利用拉曼光谱学法研究了相应结构的力学性能。其中固定在有机玻璃上的碳纳米管可等效为在基底支撑下欧拉梁的力学模型。通过对该模型进行动力学分析,可为碳纳米管性能测试及其操纵技术[17]等提供重要参考。目前,针对梁在基底支撑下的静力学变形、动力学响应及动力学稳定性等问题,相关学者已开展了大量研究工作[18-22]。然而,在这些研究中基底大多被简化为一维Winkler模型[23],即将基底等效为多个相互独立的线性弹簧,基底上任一点的作用力仅与该点变形成正比。由于有机玻璃属于典型的黏弹性材料,采用Winkler模型并不能反映其黏弹性特性,因此为了更好地分析碳纳米管在有机玻璃上的动力学特性,必须引入黏弹性基底力学模型。
非局部理论[24-25]能较好地弥补经典局部理论在纳米尺度下的不足[2,26],在碳纳米管动力学问题研究中得到了广泛应用。目前,学者利用非局部理论对碳纳米管在基底或周围介质支撑下的动力学问题做了大量研究,并取得一定成果。Chang[2]根据热弹性力学及非局部弹性理论分析了欧拉梁在Winkler线弹性介质中的热力学振动及扭转稳定性问题; Fang及Zhen等[9]采用非局部弹性理论建立了双壁碳纳米管在Winkler线弹性介质中的动力学控制方程,并对其非线性自由振动问题做了相关研究;Fotouhi和Firouz-Abadi等[10]通过非局部连续壳模型就弹性介质中纳米锥自由振动问题进行了研究,其中弹性介质简化为Winkler和Pasternak模型;Kiani[11]针对任意边界条件下粗短双壁碳纳米管在弹性基底上受轴向载荷时的振动问题,采用非局部理论求得了动力学控制方程的解析解;Arani等[27]则基于非局部理论和Winkler模型分析了氮化硼纳米管的非线性振动及不稳定性。就目前而言,针对碳纳米管在黏弹性基底上的动力学问题的研究还很少。本文提出了一种研究碳纳米管在黏弹性基底上动力学特性的新方法,可为相关问题研究提供有益参考。
1动力学控制方程
阻尼碳纳米管在黏弹性基底上的简化力学模型如图1所示,碳纳米管的长度为L,安放在位于[x1,x2]内的黏弹性基底上。下面通过建立振动控制方程对其动力学特性问题进行研究。

图1 黏弹性基底支撑下的阻尼碳纳米管Fig.1 Damped carbon nanotube with a viscoelastic foundation
1.1 非局部黏弹性理论
针对均匀各向同性弹性材料,Eringen提出的非局部弹性理论[28]将非局部应力张量tij和局部应力张量σij表述为:

(1)
σij(x′)=λeεkk(x′)δij+2μeεij(x′)
(2)
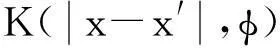
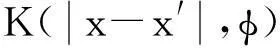
[1-(e0a)22]tij=σij
(3)
将该非局部弹性理论模型推广到黏弹性材料中,有[30]:

(4)
广义Maxwell黏弹性模型(如图2所示)的松弛模量为:
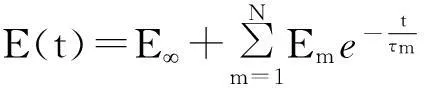
(5)
式中,τm=ηm/Em为松弛时间(其中,ηm为材料阻尼,Em为材料刚度)。

图2 广义Maxwell模型Fig.2 General Maxwell model
根据Boltzmann迭加原理,可得碳纳米管的本构方程为:

(6)
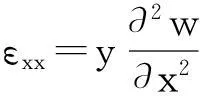
根据式(4)、式(5)和式(6),可得[31]:
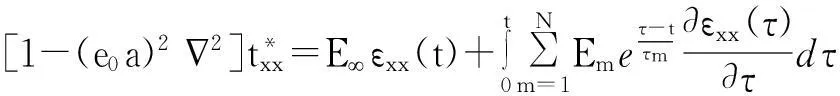
(7)
1.2 运动平衡方程
在基底支撑区域[x1,x2]上选取微元dx并进行受力分析(如图1所示),得到微元dx的动力学平衡方程为:

(8)
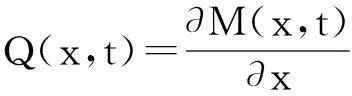
(9)
其中,A为横截面,w(x,t)为碳纳米管的横向变形,p(x,t)为分布外载荷,M(x,t)和Q(x,t)分别为弯矩和剪力,QN(x,t)为基底作用力,Ce(x,t)为外阻尼力。
式(7)两端乘以y并在横截面A上积分,得:


(10)
式中,I=∫Ay2dA表示横截面对y轴的惯性矩。
联立式(8)、式(9)和式(10),微元dx的动力学平衡方程变为:

(11)
1.3 外阻尼力及基底作用力
根据文献[31],外阻尼力Ce(x,t)取

(12)
式中,C2为外阻尼系数,μ2为黏性系数。
由Winkler模型[19]可知,基底作用力QN(x,t)与变形w(x,t)间的关系式为:
QN(x,t)=kw(x,t)
(13)
式中,k为基底刚度。
在此模型基础上考虑基底的黏弹性,则基底作用力可表示为:
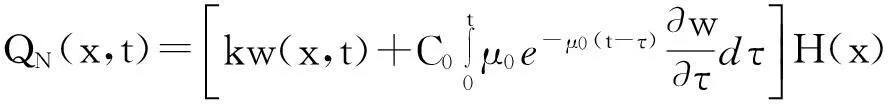
(14)
式中,C0为基底的黏弹性阻尼系数,H(x)=[H0(x-x1)-H0(x-x2)],H0(x)为阶跃函数。
1.4 动力学控制方程
将外阻尼力表达式(12)和基底作用力式(14)代入动力学平衡方程式(11),可得:

(15)
为求解碳纳米管的固有频率ω,令p(x,t)=0,同时振动控制方程式的解形如w=W(x)exp(iωt),则式(15)可化为:

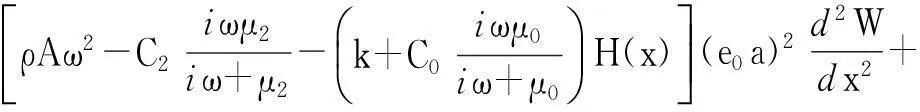
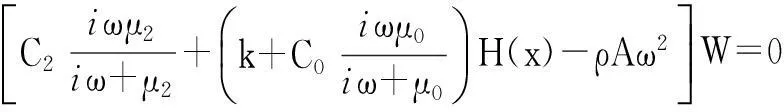
(16)
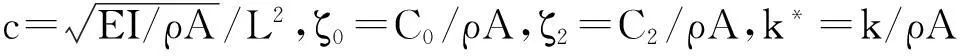
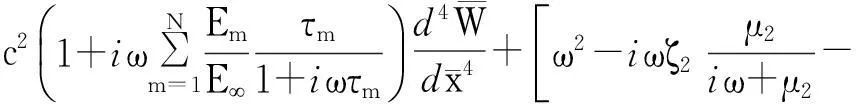
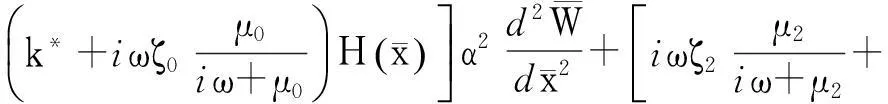
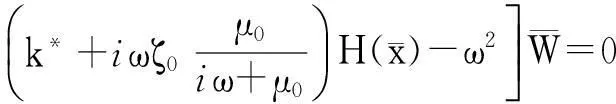
(17)
当碳纳米管端部为固支或简支时,其位移边界条件可由位移直接给出。当碳纳米管端部自由时,则需给出力边界条件,其弯矩和剪力表达式为:
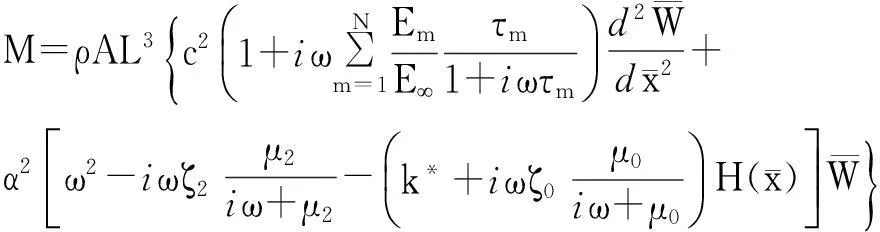
(18)
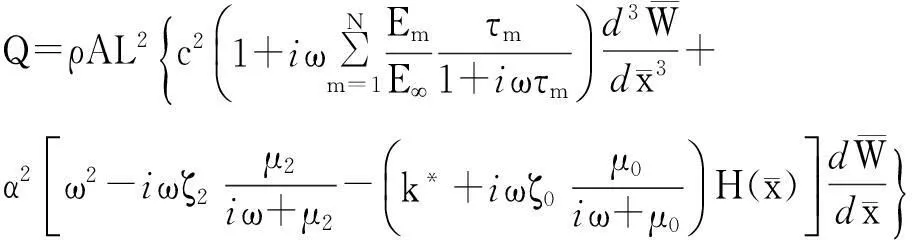
(19)

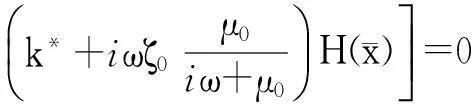
(20)
对于固支、简支等边界条件,可以确定β的取值,如两端简支时第i阶模态对应有β=iπ。假设β已知,则振动控制方程式(20)可化为关于ω的N+2次常系数多项式,则存在N+2个根,从而可确定碳纳米管的固有频率。
2非局部Kelvin-Voigt黏弹性模型
当黏弹性模型取Kelvin-Voigt模型时,有N=1和E1→,并令τd=η1/E。同时假设外阻尼和基底阻尼均为黏性阻尼(μ2→,μ0→)。
2.1 无基底支撑
基底作用力QN(x,t)中的H(x)项限定了基底的作用范围,当x1=x2时,碳纳米管无基底支撑。此时,式(20)可化为:
-(1+α2β2)ω2+[ζ2+α2β2ζ2+τdc2β4]iω+c2β4=0
(21)
对该二次方程求解,可得到固有频率为:
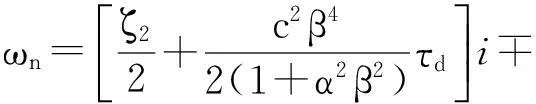
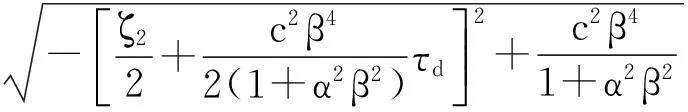
(22)
式(22)同文献[31]中无基底非局部欧拉梁固有频率表达式完全一致。
2.2 全基底支撑
当x1=0且x2=L时,碳纳米管在全长内均受基底支撑,此时式(20)可化为:

(23)
则式(23)根的一般表达式可写为:

(24)
根据特定物理意义,对固有频率的一般表达式(24)进行讨论,可得以下几种特殊情况:
1)当碳纳米管等效为无阻尼局部弹性梁时,α=τd=ζ0=ζ2=0,则固有频率为:

(25)
与熟知的欧拉梁经典解ωn=cβ2相比,考虑了基底的刚度参量k*。
2)当碳纳米管等效为有阻尼局部欧拉梁时有α=τd=0,可得固有频率为:
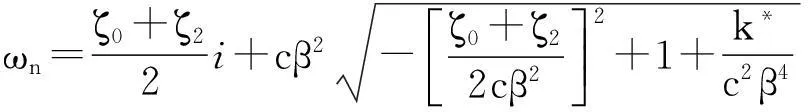
(26)
若k*=ζ0=0,则该解即为黏性阻尼欧拉梁的经典解。
3)当α=ζ0=ζ2=0时,碳纳米管为局部黏弹性梁,则有:

(27)
4)当碳纳米管等效为无阻尼非局部弹性欧拉梁时,τd=ζ0=ζ2=0,有:

(28)
若k*=0,则该解与文献[32]中无阻尼非局部欧拉梁固有频率表达式一致。
5)当等效为非局部黏弹性欧拉梁时,ζ0=ζ2=0,碳纳米管复固有频率表达式为:
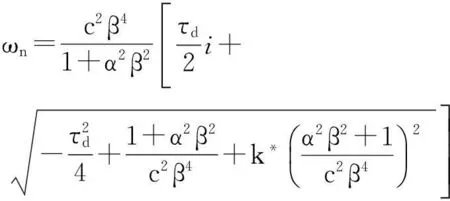
(29)
简要分析了这几种特殊情况下碳纳米管的固有频率,一般情况下,针对振动控制方程则可通过传递函数法[33](Transfer Function Method,TFM)进行求解。
3传递函数法求解

(30)
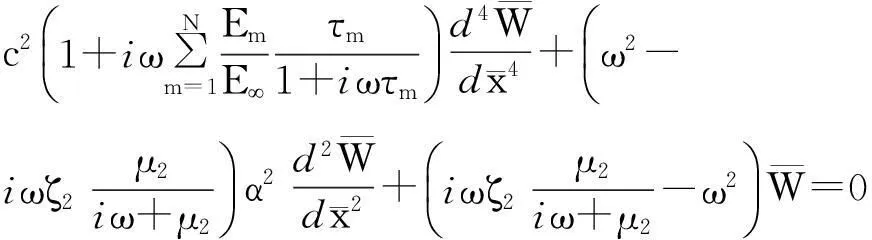
(31)
3.1 基底支撑区域
首先定义状态向量为:
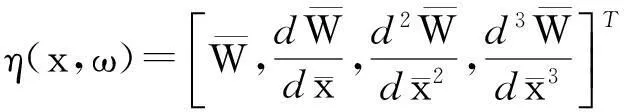
(32)
将式(30)写成状态方程形式,如式(33)所示。
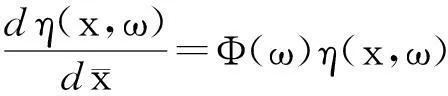
(33)
(34)
式中,


状态方程式(33)的解可写为:
(35)

η2(ω)=Ψ(ω)η1(ω)
(36)
3.2 碳纳米管整体区域
将式(31)写成状态方程形式,如式(37)所示。

(37)
式中,
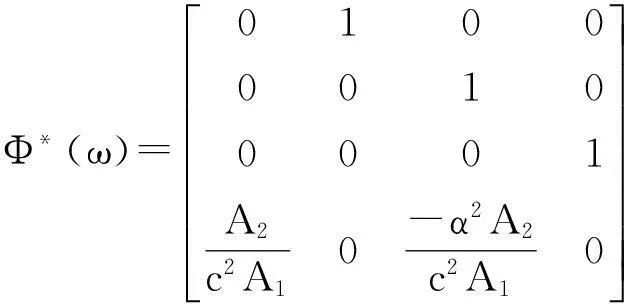
(38)
碳纳米管的边界条件可以表示为:
M(ω)ηL(ω)+N(ω)ηR(ω)=0
(39)
式中,ηL(ω)=η(0,ω),ηR(ω)=η(1,ω),M(ω)和N(ω)为碳纳米管的边界条件选择矩阵[33]。通过转换矩阵,ηR(ω)可以通过ηL(ω)表示为:
ηR(ω)=TR(ω)Ψ(ω)TL(ω)ηL(ω)
(40)

将式(40)代入式(39),则
[M(ω)+N(ω)TR(ω)Ψ(ω)TL(ω)]ηL(ω)=0
(41)
因此,系统的特征方程为:
det[M(ω)+N(ω)TR(ω)Ψ(ω)TL(ω)]=0
(42)
若ωj为其特征值,则对应的模态振型为:


(43)
4算例分析
以某单壁碳纳米管(Single-Walled Carbon NanoTubes,SWCNT)为分析对象,黏弹性模型取Kelvin-Voigt模型,分析不同边界条件下碳纳米管非局部参数、黏弹性参数以及基底刚度等对碳纳米管固有频率的影响情况。计算中涉及的主要基本参数[31]如下:SWCNT的等效半径r=0.55nm,等效壁厚δth=0.342nm,长度L=11nm,杨氏模量E=1TPa,质量密度ρ=2.24g/cm3,非局部参数α∈[0, 0.2],黏弹性模型Kelvin-Voigt中τd∈[0, 10-4],基底刚度系数k*∈[0, 3×105]。为便于分析理解,假设系统不消耗能量,黏性阻尼系数ζ0=ζ2=0。
表1给出了不同边界条件和基底支撑下弹性和黏弹性碳纳米管的前四阶固有频率。采用TFM计算得到的无基底支撑下弹性碳纳米管的固有频率与文献[32]中相关结果相吻合,验证了模型及算法的正确性。从表纵向分析可知,各阶固有频率在悬臂、简支及固支条件下受边界连接刚度的影响依次递增。从表横向分析,除悬臂梁基率外,悬臂梁后三阶固有频率和其他边界条件下各阶固有频率均随非局部参数α的增大而逐渐减小,考虑黏弹性参数τd后系统的固有频率出现了虚部,且相对无基底支撑而言,增加基底支撑后各阶固有频率明显增大。下面将在全基底支撑条件下对各参数的具体影响特性进行分析。
表1不同边界条件下不同α时固有频率对比
Tab.1Comparison of the natural frequencies of the nano-beam with different boundary conditions andα
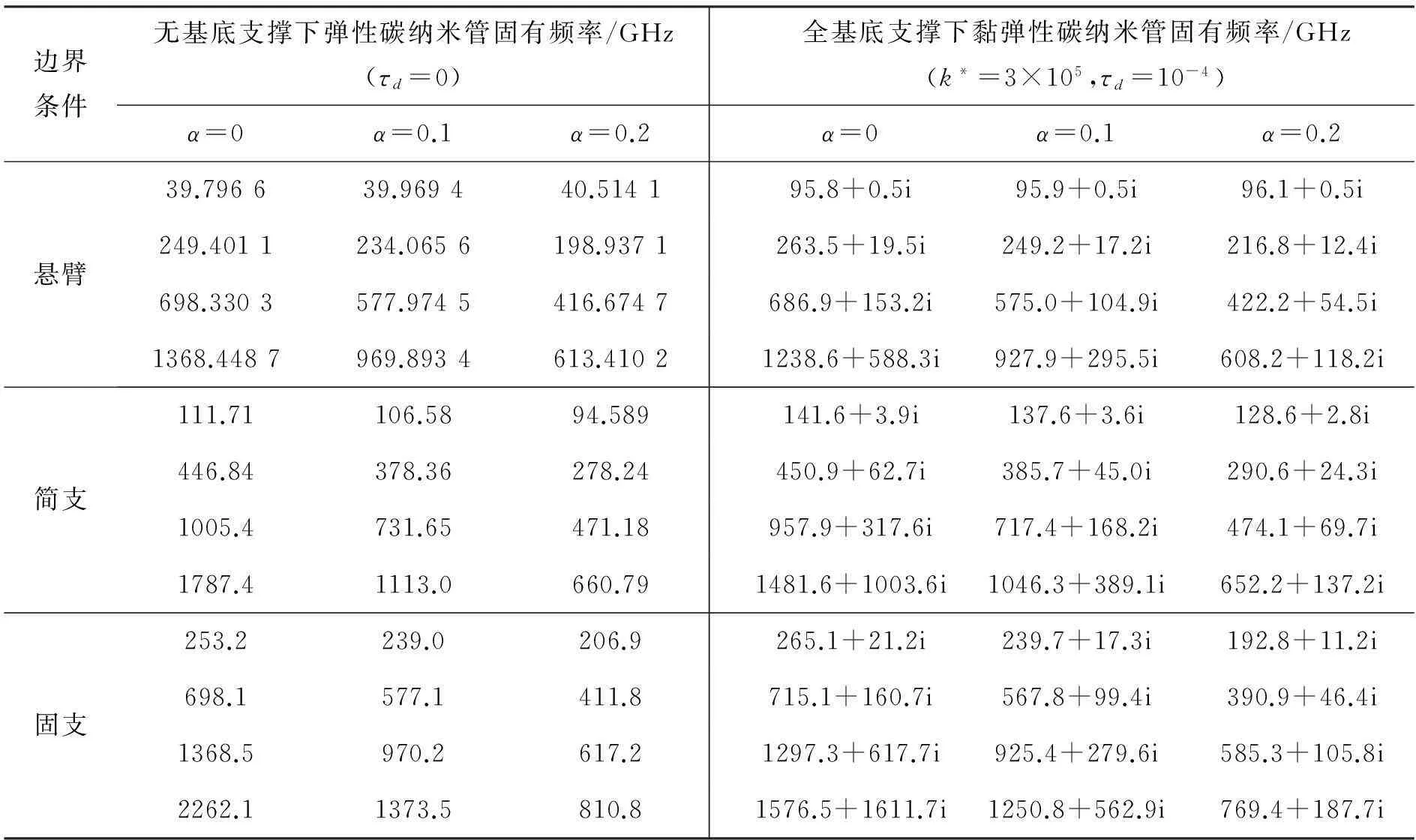
边界条件无基底支撑下弹性碳纳米管固有频率/GHz(τd=0)全基底支撑下黏弹性碳纳米管固有频率/GHz(k*=3×105,τd=10-4)α=0α=0.1α=0.2α=0α=0.1α=0.2悬臂39.796639.969440.514195.8+0.5i95.9+0.5i96.1+0.5i249.4011234.0656198.9371263.5+19.5i249.2+17.2i216.8+12.4i698.3303577.9745416.6747686.9+153.2i575.0+104.9i422.2+54.5i1368.4487969.8934613.41021238.6+588.3i927.9+295.5i608.2+118.2i简支111.71106.5894.589141.6+3.9i137.6+3.6i128.6+2.8i446.84378.36278.24450.9+62.7i385.7+45.0i290.6+24.3i1005.4731.65471.18957.9+317.6i717.4+168.2i474.1+69.7i1787.41113.0660.791481.6+1003.6i1046.3+389.1i652.2+137.2i固支253.2239.0206.9265.1+21.2i239.7+17.3i192.8+11.2i698.1577.1411.8715.1+160.7i567.8+99.4i390.9+46.4i1368.5970.2617.21297.3+617.7i925.4+279.6i585.3+105.8i2262.11373.5810.81576.5+1611.7i1250.8+562.9i769.4+187.7i
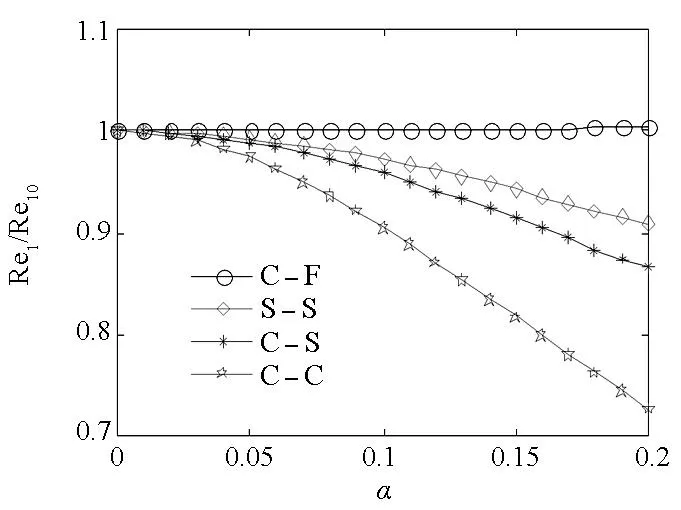
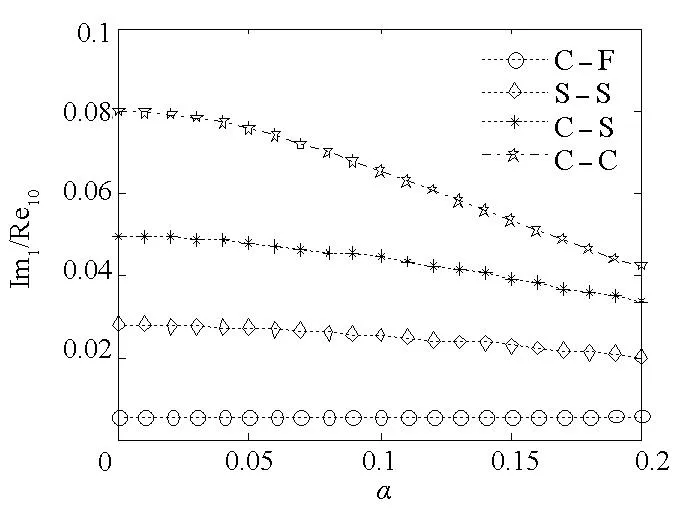
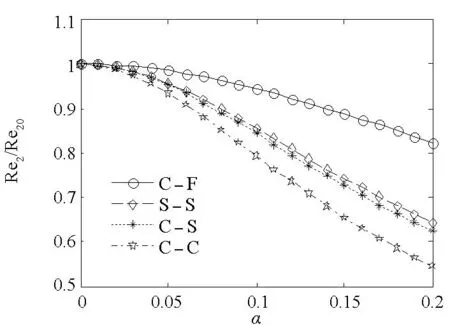
不同边界条件下非局部参数α对频率比Rei/Rei0及Imi/Rei0的影响曲线如图3所示,其中Rei和Imi分别为第i阶固有频率的实部和虚部,Rei0为所分析参数为初始值时的第i阶固有频率实部。从图3 (a)和图3(b)可以看出,悬臂梁(C-F)的一阶固有频率随α的变化很小,近似水平;两端简支(S-S)、固支-简支(C-S)及两端固支(C-C)时一阶固有频率均随α的增大而减小,且减小幅度依次递增,即固有频率对α的敏感度随边界连接刚度的提高而增大。对比图3(c)和图3(d),二阶固有频率在各边界条件下具有相似规律,且α的影响程度随固有频率阶次的增加而增大,其变化规律与碳纳米管复固有频率解析表达式(29)相符。
图4给出了碳纳米管前两阶固有频率虚部随黏弹性参数τd的变化曲线。从图中可以看出,各边界条件下前两阶固有频率虚部随τd呈线性增大,与固有频率解析表达式(29)的虚部表达式[c2β4/(2+2α2β2)]τdi相一致。同时可以看出,碳纳米管在悬臂、简支、固支-简支及固支条件下受τd的影响程度依次递增,即各阶固有频率虚部对τd的敏感度随边界连接刚度的提高而增大。对复固有频率表达式(29)的实部进行分析,发现各边界条件下松弛时间τd对固有频率实部的影响很小。
基底刚度系数k*对碳纳米管前两阶固有频率影响曲线如图5所示。前两阶固有频率在不同边界条件下随刚度系数k*的增大而逐渐增大,且两端固支梁增大幅度很小,而悬臂梁则有明显增大,刚度系数k*从0增大到3×105时,一阶固有频率实部增大了近1.4倍,即碳纳米管对k*的影响敏感度随边界连接刚度的增大而逐渐减小。同时可以看出,基底刚度k*对固有频率的影响随阶次的增加而减小。通过分析复固有频率解析表达式(29)的虚部可知,各边界条件下碳纳米管固有频率虚部不受基底刚度系数k*的影响。
(a)一阶实部(a) Real part of the first natural frequencies
(b)一阶虚部(b) Imaginary part of the first natural frequencies
(c)二阶实部(c) Real part of the second natural frequencies

(d)二阶虚部(d) Imaginary part of the second natural frequencies图3 不同边界条件下前两阶复固有频率随非局部参数α的变化情况Fig.3 Variation of the first two complex natural frequencies with α in different boundary conditions

(a)一阶虚部(a) Imaginary part of the first natural frequencies

(b)二阶虚部(b) Imaginary part of the second natural frequencies图4 不同边界条件下前两阶复固有频率随松弛时间τd的变化情况Fig.4 Variation of the first two complex natural frequencies with τd in different boundary conditions

(a)一阶实部(a) Real part of the first natural frequencies
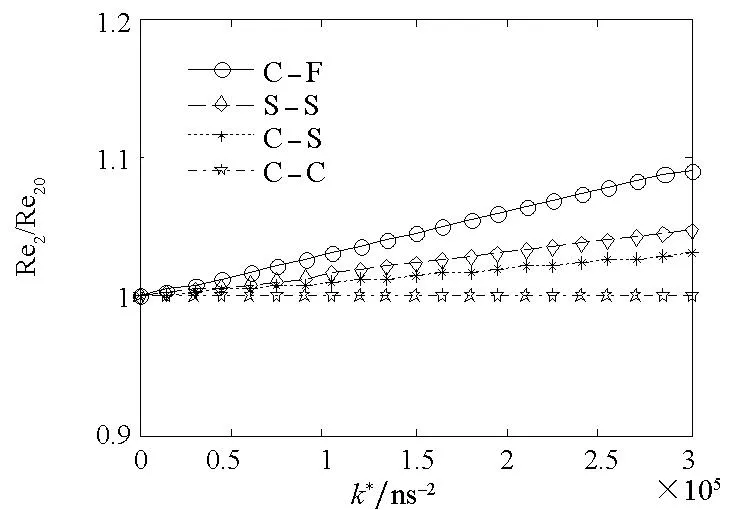
(b)二阶实部(b) Real part of the second natural frequencies图5 不同边界条件下前两阶复固有频率随基底刚度系数k*的变化情况Fig.5 Variation of the first two complex natural frequencies with k* in different boundary conditions

(a)一阶实部(a) Real part of the first natural frequencies

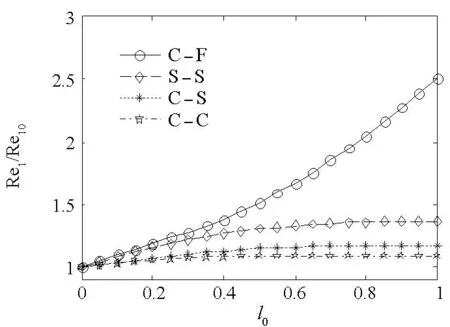
(b)二阶实部(b) Real part of the second natural frequencies图6 不同边界条件下前两阶复固有频率随基底长度l0的变化情况Fig.6 Variation of the first two complex natural frequencies with l0 in different boundary conditions
5结论
采用欧拉梁模型建立了有阻尼碳纳米管在黏弹性基底上的动力学问题分析模型。通过引入非局部理论、广义Maxwell黏弹性模型、速度相依的外阻尼模型及黏弹性基底模型,建立了碳纳米管动力学分析的欧拉梁振动控制方程。基于Kelvin-Voigt黏弹性模型,在特定边界条件下给出了碳纳米管固有频率的一般精确解析式,并分析讨论了多种典型情况。分析表明,无基底支撑时有/无阻尼的经典局部欧拉梁及非局部欧拉梁均是所建模型的特殊情况。
利用传递函数方法得到了一般边界条件下碳纳米管的振动控制方程的封闭解。以某单壁碳纳米管为算例,得到了不同边界条件下SWCNT的前四阶固有频率,并分析了碳纳米管非局部参数、黏弹性参数、基底刚度及长度等影响因素的动力学特性。其主要结论有:
1)无基底支撑时碳纳米管固有频率与已有文献中结果吻合,验证了所建模型及计算方法的正确性;
2)非局部参数α对固有频率的实部和虚部均有较大影响,且影响程度随碳纳米管边界连接刚度和频率阶次的增大而增大;
3)不同边界条件下各阶固有频率实部受碳纳米管松弛时间τd影响很小,而虚部则随τd的增大近似呈线性增加;
4)基底刚度及长度对各阶固有频率虚部影响均很小,而实部则随之增大而增大,同时基底刚度和长度的影响程度随频率阶次增高而减小。
参考文献(References)
[1]Iijima S. Helical microtubules of graphitic carbon[J]. Nature, 1991, 354: 56-58.
[2]Chang T P. Thermal-mechanical vibration and instability of a fluid-conveying single-walled carbon nanotube embedded in an elastic medium based on nonlocal elasticity theory[J]. Applied Mathematical Modelling, 2012, 36(5): 1964-1973.
[3]Chung D S, Lee S H, Choi H W, et al. Carbon nanotube electron emitters with a gated structure using backside exposure processes[J]. Applied Physics Letters,2002, 80(21): 4045-4047.
[4]Tans S J, Verschueren A R M, Dekker C. Room-temperature transistor based on a single carbon nanotube[J]. Nature,1998, 393: 49-52.
[5]Calvert P. Nanotube composites: a recipe for strength[J]. Nature, 1999, 399: 210-211.
[6]Young C C, Young M S, Dong J B, et al. Patterned growth and field emission properties of vertically aligned carbon nanotubes[J]. Diamond and Related Materials, 2001, 10(8):1457-1464.
[7]Ko Y K, Geng J X, Jang S G, et al. Enhanced field emission of an electric field assisted single-walled carbon nanotube assembly in colloid interstices[J]. Carbon, 2009, 47(6):1555-1560.
[8]Lee T W,Jeong Y G. Enhanced electrical conductivity, mechanical modulus, and thermal stability of immiscible polylactide/polypropylene blends by the selective localization of multi-walled carbon nanotubes[J]. Composites Science and Technology, 2014, 103:78-84.
[9]Fang B, Zhen Y X, Zhang C P, et al. Nonlinear vibration analysis of double-walled carbon nanotubes based on nonlocal elasticity theory[J]. Applied Mathematical Modelling, 2013, 37(3): 1096-1107.
[10]Fotouhi M M, Firouz-Abadi R D, Haddadpour H. Free vibration analysis of nanocones embedded in an elastic medium using a nonlocal continuum shell model[J]. International Journal of Engineering Science, 2013, 64: 14-22.
[11]Kiani K. Vibration analysis of elastically restrained double-walled carbon nanotubes on elastic foundation subjected to axial load using nonlocal shear deformable beam theories[J]. International Journal of Mechanical Sciences, 2013, 68: 16-34.
[12]Li X F, Wang B L, Mai Y W. Effects of a surrounding elastic medium on flexural waves propagating in carbon nanotubes via nonlocal elasticity[J]. Journal of Applied Physics, 2008, 103(7):074309.
[13]Wu J X, Li X F, Tang G J. Bending wave propagation of carbon nanotubes in a bi-parameter elastic matrix[J]. Physica B: Condensed Matter, 2012, 407(4):684-688.
[14]Cooper C A, Young R J, Halsall M. Investigation into the deformation of carbon nanotubes and their composites through the use of Raman spectroscopy [J]. Composites Part A: Applied Science and Manufacturing, 2001, 32(3/4):401-411.
[15]Young R J, Kinloch I A, Gong L, et al. The mechanics of graphene nanocomposites:a review[J]. Composites Science and Technology, 2012, 72(12): 1459-1476.
[16]Raju A P A, Lewis A, Derby B, et al. Wide-area strain sensors based upon graphene-polymer composite coatings probed by Raman spectroscopy[J].Advanced Functional Materials, 2014, 24(19): 2865-2874.
[17]吴森. 基于AFM的一维纳米材料操纵及力学特性测试技术[D]. 天津:天津大学, 2011.
WU Sen. Manipulation and force measurement technology of one-dimensional nanomaterials using atomic force microscopy(AFM)[D]. Tianjin: Tianjing University, 2011. (in Chinese)
[18]Yankelevsky D Z, Eisenberger M. Analysis of a beam column on elastic foundation[J]. Computers & Structures, 1989, 23(3): 351-356.
[19]Thambiratnam D, Zhuge Y. Free vibration analysis of beams on elastic foundation[J]. Computers & Structures, 1996, 60(6): 971-980.
[20]Sun L. A closed form solution of a Bernoulli-Euler beam on a viscoelastic foundation under harmonic line loads[J]. Journal of Sound and Vibration, 2001, 242(4): 619-627.
[21]Lei Y J, Friswell M I, Adhikari S. Finite element analysis of beams with nonlocal foundation[C]//Proceedings of 47th AIAA/ASME/ASCE/ ASC Structures, Structural Dynamic, and Materials Confere, Newport, Rhode Island, AIAA 2006-1742, 2006: 1-11.
[22]Kim S M. Vibration and stability of axial loaded beams on elastic foundation under moving harmonic loads[J]. Engineering Structures, 2004, 26(1): 95-105.
[23]Cigeroglu E, Samandari H. Nonlinear free vibrations of curved double walled carbon nanotubes using differential quadrature method[J]. Physica E:Low-dimensional Systems and Nanostructures, 2014, 64:95-105.
[24]Eringen A C. Nonlocal polar elastic continua[J]. International Journal of Engineering Science, 1972, 10(1): 1-16.
[25]Eringen A C, Edelen D G B. On nonlocal elasticity [J]. International Journal of Engineering Science, 1972,10(3): 233-248.
[26]Roostai H, Haghpanahi M. Vibration of nanobeams of different boundary conditions with multiple cracks based on nonlocal elasticity theory[J]. Applied Mathematical Modelling, 2014, 38(3): 1159-1169.
[27]Arani A G, Kolahchi R, Maraghi Z K. Nonlinear vibration and instability of embedded double-walled boron nitride nanotubes based on nonlocal cylindrical shell theory[J]. Applied Mathematical Modelling, 2013, 37(14/15): 7685-7707.
[28]Eringen A C. Nonlocal continuum field theories [M]. New York, USA: Springer, 2002.
[29]Eringen A C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves[J]. Journal of Applied Physics, 1983, 54(9):4703-4710.
[30]Lei Y, Adhikari S, Friswell M I. Vibration of nonlocal Kelvin-Voigt viscoelastic damped Timoshenko beams[J]. International Journal of Engineering Science, 2013, 66-67:1-13.
[31]Lei Y, Murmu T, Adhikari A, et al. Dynamic characteristics of damped viscoelastic nonlocal Euler-Bernoulli beams[J]. European Journal of Mechanics A/Solids, 2013, 42:125-136.
[32]Lu P, Lee H P, Lu C, et al. Dynamic properties of flexural beams using a nonlocal elasticity model[J]. Journal of Applied Physics, 2006, 99:1-9.
[33]Yang B, Tan C A. Tranfer functions of one-dimensional distributed parameter systems [J]. Journal of Applied Mechanics, 1992, 59(4): 1009- 1014.
http://journal.nudt.edu.cn
Dynamic characteristics of damped carbon nanotubes on viscoelastic foundations
ZHANGDapeng,LEIYongjun
(College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China)
Abstract:The dynamic characteristic analysis model of damped carbon nanotubes on viscoelastic foundations was built by using Euler-Bernoulli beams. The nonlocal viscoelastic theories, general Maxwell viscoelastic model, velocity-dependent external damping model and viscoelastic foundation model were employed to deduce the governing equation of Euler-Bernoulli beams for dynamic characteristics analysis of carbon nanotubes. On the basis of Kelvin-Voigt model, new general analytical expressions for the natural frequencies of damped carbon nanotubes with no foundation and full foundation were obtained respectively and some typical special cases at full foundation were discussed. Then a transfer function method was developed to obtain a closed-form and uniform solution for the vibration governing equation under arbitrary boundary conditions. Considering a single-walled carbon nanotube as a numerical example, the first four natural frequencies with different boundary conditions were obtained, and the effects of the nonlocal and viscoelastic constants, the foundation stiffness coefficient and length on the natural frequencies and damping factors were analyzed. Results demonstrate the efficiency of the proposed model and the analysis methods in solving dynamic problems of damped carbon nanotubes on viscoelastic foundations.
Key words:dynamic characteristics; viscoelastic foundations; Euler-Bernoulli beams; nonlocal elasticity theory; transfer function method
中图分类号:O343
文献标志码:A
文章编号:1001-2486(2015)06-141-09
作者简介:张大鹏(1989—),男,河南新乡人,博士研究生,E-mail:zhangdapenghit@126.com;雷勇军(通信作者),男,教授,博士,博士生导师,E-mail:leiyj108@nudt.edu.cn
基金项目:国家自然科学基金资助项目(11272348,11302254)
收稿日期:*2014-12-25
doi:10.11887/j.cn.201506026

