低轮PUFFIN算法的积分攻击*
赵光耀,成 磊,李瑞林,李 超,,孙 兵
(1.国防科技大学 计算机学院, 湖南 长沙 410073; 2.国防科技大学 理学院, 湖南 长沙 410073;
3.国防科技大学 电子科学与工程学院, 湖南 长沙 410073)
低轮PUFFIN算法的积分攻击*
赵光耀1,成磊2,李瑞林3,李超1,2,孙兵2
(1.国防科技大学 计算机学院, 湖南 长沙410073; 2.国防科技大学 理学院, 湖南 长沙410073;
3.国防科技大学 电子科学与工程学院, 湖南 长沙410073)
摘要:PUFFIN是一个分组长度为64bit的轻量级分组密码算法,其密钥长度为128bit。对PUFFIN抵抗积分攻击的能力进行研究,构造并证明PUFFIN算法存在5轮和6轮积分区分器。利用6轮积分区分器对8轮PUFFIN进行积分攻击,可恢复2轮共100bit轮密钥,攻击的数据复杂度为220个选择明文,时间复杂度约为233次8轮加密,存储复杂度为220,这是目前为止对PUFFIN最好的积分分析结果。
关键词:PUFFIN;轻量级分组密码;积分攻击
随着物联网等应用的兴起,适用于资源受限环境的轻量级密码算法得到了飞速发展,密码学者根据不同的应用需求设计了许多的轻量级算法,例如HIGHT[1],LBlock[2],LED[3],PRESENT[4]等。PUFFIN[5]也是一种轻量级分组密码算法,采用混淆扩散网络结构(Substitution Permutation Networks,SPN)型结构,其分组长度为64bit,密钥长度为128bit。非线性层由16个相同的4×4的S盒并置组成,线性层则为64bit置换,其S盒及P置换均为对合结构,使得其加解密结构一致,硬件实现时占用芯片面积非常小。文献[5]中,设计者对PUFFIN抵抗差分分析[6]、线性分析[7]、相关密钥攻击[8]的能力进行了分析,并分析了算法的弱密钥[9],目前对PUFFIN的第三方安全性分析结果主要有线性分析[10]和积分攻击[11]。文献[10]主要分析了PUFFIN的线性特征,并对其进行了线性攻击;文献[11]则首次对PUFFIN抵抗积分攻击的安全性进行了研究。
积分攻击[12]的原理由Knudsen和Wagner提出。自提出以后,积分攻击在许多基于字节设计的算法上得到了很好的应用,例如Camellia[13], CLEFIA[14]等。Z′aba等针对Noekeon,Serpent,Present等基于比特设计的算法对积分攻击进行了扩展,提出了基于比特的积分攻击[15]。
1基础理论
1.1 PUFFIN简介
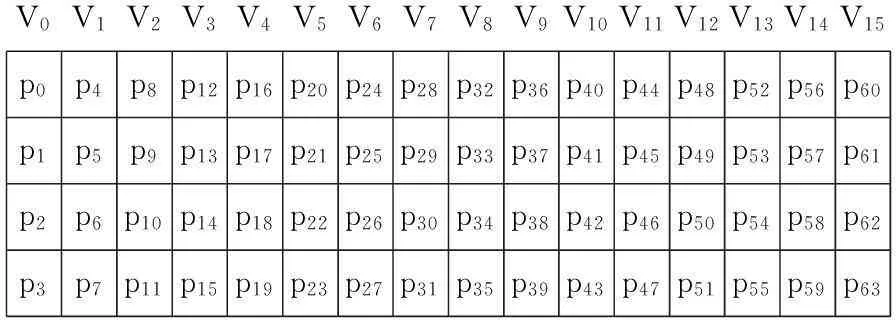
PUFFIN为SPN型结构分组密码算法,其分组长度和密钥长度分别为64bit和128bit,迭代32轮。64bit明文(中间状态,轮密钥及密文)排列成一个4行16列的二维数组形式,即p0,p1,…,p63可表示成V0, V1,…, V15共16个向量,其中Vi=(p4i,p4i+1,p4i+2,p4i+3)T,0≤i≤15,如图1所示。
V0V1V2V3V4V5V6V7V8V9V10V11V12V13V14V15p0p4p8p12p16p20p24p28p32p36p40p44p48p52p56p60p1p5p9p13p17p21p25p29p33p37p41p45p49p53p57p61p2p6p10p14p18p22p26p30p34p38p42p46p50p54p58p62p3p7p11p15p19p23p27p31p35p39p43p47p51p55p59p63
图1PUFFIN分组比特顺序
Fig.1Block state of PUFFIN
轮函数包含以下3个变换:
1)非线性层γ由16个相同的4×4的S盒并置组成,每列(Vi)通过1个S盒。S盒映射见表1。

表1 S盒映射(16进制表示)
性质(S盒表达式)设x=(x3,x2,x1,x0)和y=(y3,y2,y1,y0)分别表示S盒的输入和输出(如图2所示),则x和y满足:
y0=x0x1x2+x0x1x3+x0x1+x0x2+x0x3+x1x2+x2x3+1,
y1=x0x1x3+x0x1+x0+x1x2+x1+x3,
y2=x0x1x2+x0x2x3+x1x2x3+x1x3+x1+x2x3+x2+1,
y3=x0x1x3+x0x1+x0x2+x0+x1x2x3+x1x2+x1+x2x3+1。

图2 S盒的输入输出Fig.2 Input and output of S box
2)密钥加σ∶64bit的轮密钥与64bit的状态进行异或。
3)线性层进行P64 ∶64bit的一个置换,其映射见表2。变换输入为(行标× 8 + 列标 + 1),如表2中(0,0)位置对应的元素为13,即P64(0× 8 + 0+ 1)=P64(1)=13。
加密之初,首先进行密钥白化以及一个P64转换,然后进行32轮轮函数的迭代,所以PUFFIN加密过程可表示为
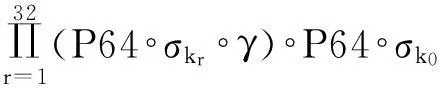


表2 P64映射
1.2 基于比特的积分攻击
Z′aba等提出的基于比特的积分,实际上是基于计数方法来进行的,通过统计每个比特上不同元素出现的奇偶次数来判断其平衡性。实际上,通过布尔函数的最高次项系数取值也可以判定其平衡性。

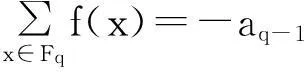
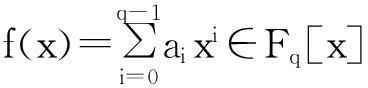
定理1说明,要确定密文某个位置是否平衡,可通过研究该位置密文与明文之间多项式函数的最高项系数来判断。定理2则给出了一个判断最高项系数的方法。
令deg(f)表示f的最高次数,若密文某个比特位置的表达式f对任意的c0,c1,…,cn-m-1都满足
deg(f) ≤m-1,
则对此位置上出现的所有2m个元素(g0,g1,…,g2m-1)求和有
∑gi=0,0 ≤i≤ 2m-1,
即对应的多项式函数最高次项系数为0,此时该比特是平衡的。
2PUFFIN的积分攻击
2.1 PUFFIN的5轮积分区分器
定理3设明文为P= (p0,p1,…,p63) ,则当(p6,p24,p31,p60)遍历{0,1}4时, 5轮加密后密文有29个比特是平衡的。
证明:当输入明文的活跃位置为p6,p24,p31,p60时,状态可表示为:
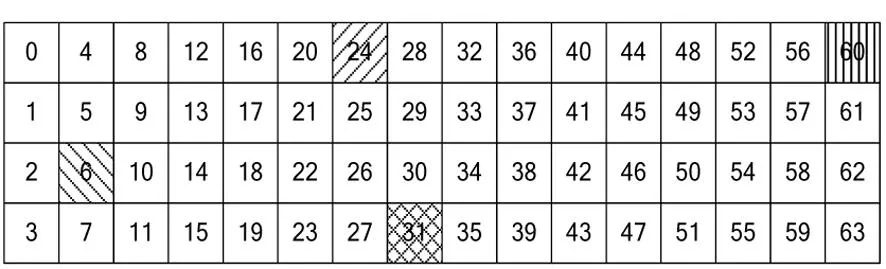
方格内数字表示比特顺序,每一轮开始时重新编号。
经过P64后,活跃位置将位于同一列,即为:

再经过第1轮的S盒后,状态为:
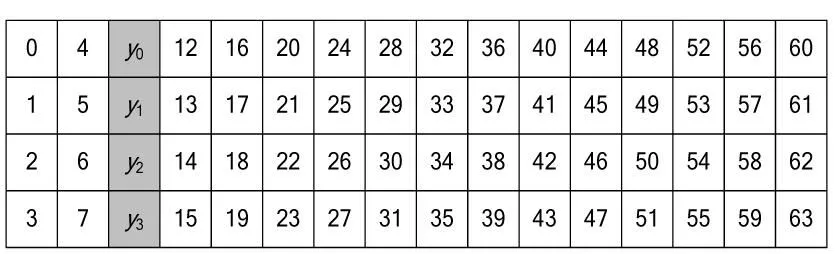
记这4个位置的变量分别为y0,y1,y2,y3,则经过第1轮的P64后,状态变为:

灰色底纹标记的位置标注有当前比特表达式的最高次项,无底纹的位置为常数,即其取值不受yi影响。
经过第2轮的S盒后,状态变为:

再经过P64状态为:

经过第3轮的S盒后,依据性质1,状态变为:
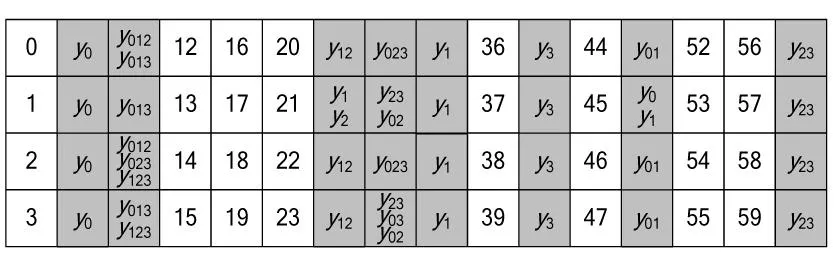
其中yijk表示此比特表达式的最高次项为yiyjyk,0≤i,j,k≤3。第3轮的输出状态为:
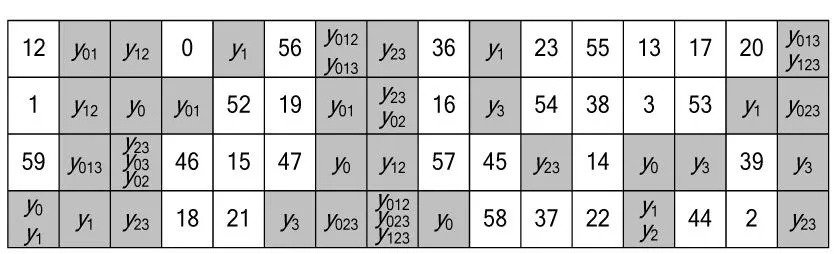
依此类推,可得第4轮的输出状态为:
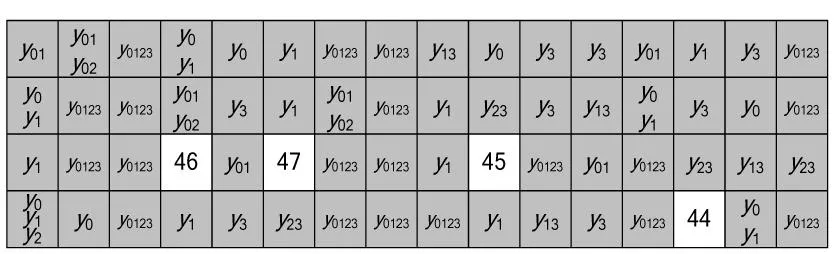
第5轮的输出状态为:

综上讨论,当(p6,p24,p31,p60)遍历{0,1}4时, (y0,y1,y2,y3)也取遍24个值,则5轮加密后的密文中灰色底纹标记的比特位置关于y0,y1,y2,y3的布尔函数f(y0,y1,y2,y3),满足deg(f)≤ 3,因此这些比特位置平衡。
□
2.2 PUFFIN的6轮积分区分器
在5轮积分区分器前加1轮,可将其扩展至6轮的积分区分器。
定理4当明文的16个比特{p5,p8,p9,p10,p11,p26,p27,p28,p29,p30,p35,p42,p50,p51,p61,p63}遍历{0,1}16时,6轮PUFFIN算法加密后密文的平衡比特与2.1节所述的5轮积分区分器输出平衡位置相同。
证明:如图3所示,当{p5,p8,p9,p10,p11,p26,p27,p28,p29,p30,p35,p42,p50,p51,p61,p63}遍历{0,1}16时,经过白化和P64变换后,输出状态的V1,V6,V7,V15的级联遍历{0,1}16,经过第1轮非线性层后,第6、第24、第31和第60比特遍历{0,1}4,从而满足5轮积分区分器的输入状态,故原5轮积分区分器的平衡位置在该6轮积分区分器中仍然平衡。
□
上述证明说明5轮积分区分器的29个平衡位置在扩展的6轮高阶积分区分器中仍然平衡,通过实验测试验证,扩展的6轮高阶积分区分器有且仅有这29个平衡位置。

图3 将5轮积分区分器扩展至6轮积分区分器Fig.3 Extend the 5-round integral distinguisher to the 6-round one
2.3 对8轮PUFFIN的积分攻击
利用6轮的高阶积分区分器,可以对8轮的PUFFIN进行积分攻击,从而可获取部分轮密钥信息。如图4所示。

图4 8轮PUFFIN算法的积分攻击Fig.4 Integral attack on 8-round PUFFIN
攻击的主要思想是通过猜测第8轮的轮密钥RK(8)及第7轮的轮密钥RK(7)的部分比特,对密文进行部分解密后,观测第6轮输出的对应位置是否平衡来筛选密钥。当选择不同的平衡位置进行密钥筛选时,能够筛选的RK(8)和RK(7)的密钥字(4bit)是不同的,平衡位置与可筛选的密钥字间的对应关系见表3。

表3 选择平衡位置与可筛选密钥字的对应关系
以44, 45, 46, 47这4个平衡位置为例,其攻击步骤为:
1)选择一组明文(其中{p5,p8,p9,p10,p11,p26,p27,p28,p29,p30,p35,p42,p50,p51,p61,p63}取遍{0,1}16,其余位置为常数,故一组明文包含216个明文)进行8轮加密,密文记为C0,C1,…,C216-1。
2)猜测RK(8)的4个密钥字(共16bit)RK3(8),RK5(8),RK9(8),RK13(8),计算Qj(i)=γ-1(P64-1(Ci)RKj(8)),j∈{3,5,9,13}。
3)计算Ti=P64-1(Q(i)),猜测RK(7)的一个密钥字RK11(7),计算t=S-1(T11iRK11(7))。
4)判断t是否为0,若t=0,则猜测的RK3(8),RK5(8),RK9(8),RK13(8),RK11(7)正确,否则,淘汰。
5)重新选取一组明文,重复上述步骤,直到唯一确定RK3(8),RK5(8),RK9(8),RK13(8)和RK11(7)。

实验及结果:在PC机上利用C++(Visual C++6.0)编程模拟了密钥筛选过程。实验中每组明文的常数值随机生成,首先考虑当11次筛选均对20bit轮密钥进行筛选时(重复筛),共做了500次模拟实验,统计唯一确定20bit密钥平均所需的明文组数。实验结果如图4所示。
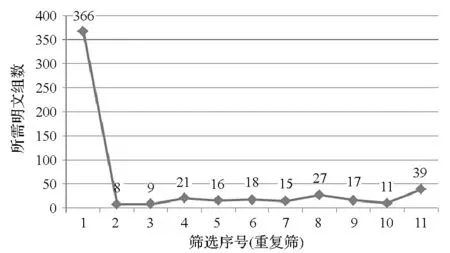
图4 唯一确定密钥所需明文组数(重复筛选时)Fig.4 Group number of plaintexts to find the right key (when each filtration works on 20bit keys)
若在筛选过程中,已经确定的密钥字不再重新筛选(不重复筛),统计唯一确定猜测密钥字所需的明文组数。图5所示为500次模拟实验的平均结果。
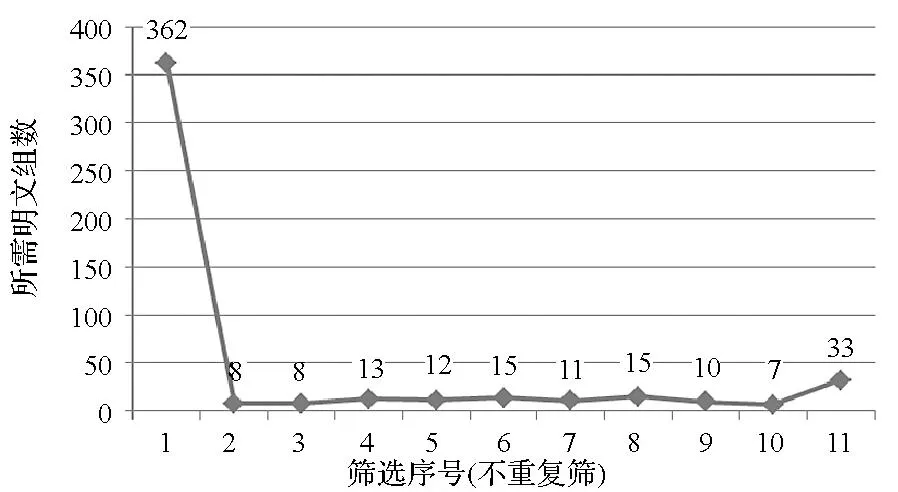
图5 唯一确定密钥所需明文组数(不重复筛选时)Fig.5 Group number of plaintexts to find the right key (when filtrating step by step)
实验结果显示,大部分筛选使用约16组明文即可唯一确定正确密钥(攻击时可按照所需明文组数由少到多的顺序进行筛选,保证前面的筛选能够将密钥字唯一确定)。当使用平衡位置{56,59}以及{44,45,46,47}进行筛选时,需要的明文组较多,这主要是由于这些平衡位置比较特殊,对于猜测的RK(7)密钥字的所有可能取值,这些位置以较大概率保持平衡,所以在确定正确密钥过程中需要的明文组数很多。
3结论
利用基于比特的积分思想对PUFFIN算法进行了积分分析,构造并证明了算法存在5轮和6轮积分区分器,对8轮PUFFIN算法进行了积分攻击。构造的积分区分器输出的平衡位置较多,因此对8轮PUFFIN算法进行积分攻击时效率较高,恢复100bit轮密钥所需的数据复杂度为220个选择明文,时间复杂度为233次8轮加密,存储复杂度为220。
参考文献(References)
[1]Hong D, Sung J, Hong S,et al. HIGHT: a new block cipher suitable for low-resource device[C]//Proceedings of Cryptographic Hardware and Embedded Systems,2006,4249: 46-59.
[2]Wu W L, Zhang L. LBlock: a lightweight block cipher[C] //Proceedings of Applied Cryptography and Network Security,2011,6715: 327-344.
[3]Guo J, Peyrin T, Poschmann A, et al. The LED block cipher[C] //Proceedings of Cryptographic Hardware and Embedded Systems, 2011,6917: 326-341.
[4]Bogdanov A, Knudsen L, Leander G,et al. PRESENT: an ultra-lightweight block cipher[C]//Proceedings of Cryptographic Hardware and Embedded Systems,2007,4727: 450-466.
[5]Cheng H, Heys H, Wang C. PUFFIN: a novel compact block cipher targeted to embedded digital systems[C] //Proceedings of 11thEUROMICRO Conference on Digital System Design: Architectures, Methods and Tools,2008: 383-390.
[6]Biham E,Shamir A. Differential cryptanalysis of DES-like cryptosystems[C] //Proceedings of Advances in Cryptology: CRYPTO′90, 1990,537: 2-21.
[7]Matsui M. Linear cryptanalysis method for DES cipher[C]//Proceedings of Advances in Cryptology: EUROCRYPT ′93,1993,765: 386-397.
[8]Biham E. New type of cryptanalytic attacks using related keys[J]. Journal of Cryptology, 1994,7(4): 229-246.
[9]Moore J H, Simmons G J. Cycle structure of the DES for keys having palindromic (or antipalindromic) sequences of round keys[J]. IEEE Transactions on Software Engineering, 1987, 13(2):262-273.
[10]Leander G. On linear hulls, statistical saturation attacks, PRESENT and a cryptanalysis of PUFFIN[C] //Proceedings of Advances in Cryptology-EUROCRYPT,2011,6632: 303-322.
[11]魏悦川,孙兵,李超. 一 种PUFFIN类 SPN型分组密码的积分攻击[J]. 国防科技大学学报, 2010, 32(3): 139-143.
WEI Yuechuan, SUN Bing, LI Chao. An integral attack on PUFFIN and PUFFIN-like SPN cipher[J]. Journal of National University of Defense Technology, 2010, 32(3): 139-143. (in Chinese)
[12]Knudsen L, Wagner D. Integral cryptanalysis[C]//Proceedings of Fast Software Encryption, 2002, 2365: 112-127.
[13]Lei D, Li C, Feng K Q. New observation on camellia[C]//Proceedings of Selected Areas in Cryptography, 2005, 3897: 51-64.
[14]王薇,王小云.对CLEFIA算法的饱和度分析[J].通信学报, 2008, 29(10): 88-92.
WANG Wei, WANG Xiaoyun. Saturation cryptanalysis of CLEFIA[J]. Journal on Communications, 2008,29(10): 88-92. (in Chinese)
[15]Z′aba M R, Raddum H, Henricksen M,et al. Bit-pattern based integral attack[C] //Proceedings of Fast Software Encryption, 2008, 5086: 363-381.
[16]李超, 孙兵, 李瑞林. 分组密码的攻击方法与实例分析[M]. 北京:科学出版社, 2010.
LI Chao, SUN Bing, LI Ruilin. Cryptanalytic methods and instance analysis of block ciphers[M].Beijing:Science Press, 2010.(in Chinese)

http://journal.nudt.edu.cn
Integral cryptanalysis on reduced-round PUFFIN
ZHAOGuangyao1,CHENGLei2,LIRuilin3,LIChao1,2,SUNBing2
(1. College of Computer, National University of Defense Technology, Changsha 410073, China;
2.College of Science, National University of Defense Technology, Changsha 410073, China;
3.College of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)
Abstract:PUFFIN is a lightweight block cipher, in which the block length is 64 bit while the key size is 128 bit. The integral cryptanalysis resistance ability of PUFFIN was analyzed. The existence of 5 and 6 round integral distinguisher in PUFFIN was constructed and proved. An integral attack on 8 round PUFFIN was mounted by 6 round integral distinguisher to recover 2 round 100 bit round cipher. The data complexity of the attack is 220chosen plaintexts, the time complexity is about 2338 round encryptions, and the space complexity is 220. This has been the best integral attack on PUFFIN up to now.
Key words:PUFFIN; lightweight block cipher; integral attack
中图分类号:TN918
文献标志码:A
文章编号:1001-2486(2015)06-129-06
作者简介:赵光耀(1982—),男,湖南湘潭人,博士研究生,E-mail:securityzgy@163.com;孙兵(通信作者),男,讲师,博士,E-mail:happycome@163.com
基金项目:国家自然科学基金资助项目(61402515);信息保障技术国家重点实验室开放基金资助项目(KJ-14-003)
收稿日期:*2015-01-12
doi:10.11887/j.cn.201506024

