载波相位辅助的卫星导航天线阵抗干扰算法*
陈飞强,聂俊伟,苏映雪,王飞雪
(国防科技大学 电子科学与工程学院, 湖南 长沙 410073)
载波相位辅助的卫星导航天线阵抗干扰算法*
陈飞强,聂俊伟,苏映雪,王飞雪
(国防科技大学 电子科学与工程学院, 湖南 长沙410073)
摘要:针对卫星导航接收机的抗干扰问题,提出一种基于载波相位辅助的卫星导航天线阵抗干扰算法。该算法进行盲零陷形成的同时利用各阵元通道输出信号的载波相位辅助来进行盲波束形成,并通过控制算法实现智能切换。仿真结果表明,提出的算法在干扰环境且接收机冷启动的条件下仍能成功抑制干扰、正常运行,在无干扰或弱干扰条件下能进行波束形成来增强卫星信号,从而提高卫星可见性以及定位精度。提出的算法不需要姿态测量单元辅助且对阵元幅相不一致引起的导向矢量误差不敏感,其实现代价远小于传统的波束形成算法。
关键词:卫星导航;波束形成;天线阵;抗干扰;功率倒置;载波相位
对于全球导航卫星系统(Global Navigation Satellite System, GNSS),干扰和多径是影响接收机导航定位性能的两个主要因素[1]。干扰能引起接收机信噪比恶化,导致接收机无法正确估计信号参数(例如伪码和载波相位),甚至使接收机完全无法捕获到信号。信号的多径传播尤其是短时延多径会导致接收机定位精度下降,且多径与对流层误差、钟差等误差源不同,它难以通过差分处理技术消除[2]。
GNSS在军事上的重要性要求不断提高GNSS接收机的精度以及其在干扰环境下的生存能力。自适应天线阵是一种有效的GNSS抗干扰、抗多径措施[3-5],它通过控制阵列中各阵元的增益和相位,使阵列方向图在干扰方向形成零陷来抑制干扰。若卫星信号的入射方向已知,则GNSS天线阵可进一步在信号方向形成波束来提高信号方向的增益、减小其他方向的增益,达到增强信号、减小多径干扰从而提高定位精度的目的。
对于核心应用领域尤其是军事应用而言,GNSS抗干扰接收机要求具备在干扰环境下冷启动(在没有自身位置以及指向等先验信息的条件下启动)时仍能正常工作的能力[6]。尽管接收机可通过存储的历书来获取卫星位置,但在干扰抑制前其无法获取卫星信号的导向矢量。这种情况下,传统的波束形成算法[7-8]可能无法正常运行[6]。盲抗干扰算法,例如功率倒置(Power Inversion, PI)算法[9-10]可以在无先验信息的条件下自适应地在干扰方向形成零陷,具备突出的抗干扰能力。盲抗干扰算法的缺点是无法在信号方向形成波束,未能利用天线阵来增强信号、减小多径干扰。因此尽管采用了天线阵,但在无干扰下其性能相比普通的单天线接收机没有任何优势,且天线阵实现复杂度和代价更高。文献[11-12]提出了一种利用天线阵各阵元通道接收信号的载波相位来获取卫星信号导向矢量的方法,但在干扰尤其是宽带干扰条件下,单阵元通道接收的信号难以被捕获跟踪,无法得到载波相位,因而该方法只适用于无干扰或弱干扰条件。
1阵列信号模型
考虑一个N元天线阵,假设远场处有一个期望信号(即GNSS信号,设其对应的卫星编号为k)和P个互不相干的干扰以平面波入射,则阵列接收信号矢量可表示为GNSS信号、干扰和噪声的叠加:
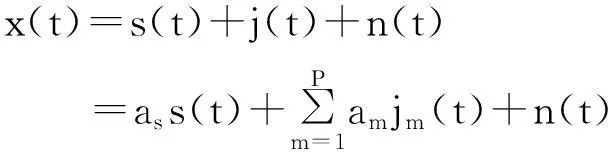
(1)
式中:x(t)为N维阵列数据矢量,x(t)=[x1(t),x2(t),…,xN(t)]T;n(t)为N维阵列噪声矢量,n(t)=[n1(t),n2(t),…,nN(t)]T,假设噪声为高斯白噪声;as为信号导向矢量,am(m= 1, 2, …,P)为第m个干扰的导向矢量,导向矢量由信号(或干扰)的入射方向以及阵元相对参考接收点的位置坐标确定;s(t)为信号的复包络,jm(t)为第m个干扰的复包络。
假设信号、干扰以及噪声之间不相关,阵列数据的相关矩阵可表示为:
Rxx=E[x(t)xH(t)]=Rss+Rjj+Rnn
(2)
各路信号经阵列权矢量w加权求和后得到阵列输出信号为:
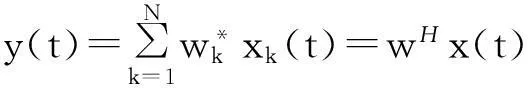
(3)
最小方差无失真响应(Minimum Variance Distortionless Response,MVDR)算法是一种传统的波束形成算法,该算法既能在干扰方向形成零陷,又能在信号方向形成波束。其基本原理是约束期望信号方向的阵列响应为1,使阵列输出信号的功率最小,MVDR算法的权矢量可表示为[6]:
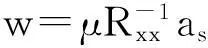
(4)
式中,μ为一常数。从式(4)可以看到,MVDR算法的权矢量表达式中含有期望信号导向矢量,而期望信号导向矢量一般通过卫星位置、接收机位置以及天线阵姿态计算得到。接收机在干扰条件下冷启动时,干扰抑制前其位置无法获得,因此该算法无法正常运行。另外,天线阵元间的幅相不一致可能引起导向矢量估计误差,从而导致算法的阵列性能下降[13]。
PI算法是一种典型的盲抗干扰算法,其基本原理是以某一个阵元接收信号作为参考,调整其他支路的阵列加权使阵列的输出功率最小。若以第一个阵元做参考,PI算法的权矢量可表示为[9]:

(5)
2载波相位辅助的抗干扰算法
算法原理框图如图1所示。输入的阵列数据分别经过盲零陷形成算法和盲波束形成算法进行处理,得到两路阵列合成输出,最后输出切换控制算法通过一定的最优准则选择某一路作为最终的输出。

图1 本文算法原理框图Fig.1 Block diagram of the proposed algorithm
2.1 盲零陷形成
盲零陷形成算法采用目前较为成熟的PI算法。由于盲零陷形成算法只形成指向干扰的零陷,不针对卫星信号方向进行波束形成,因此该算法针对所有的卫星具有相同的阵列权值和加权处理过程。根据式(3)和式(5),盲零陷形成算法的输出可表示为:
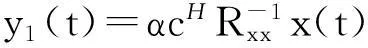
(6)
从式(6)可以看到,该算法不需要卫星位置、接收机位置、天线阵姿态等先验信息,即使在干扰环境下冷启动时也可正常运行来抑制干扰,接收信号。
2.2 盲波束形成
在无干扰或弱干扰条件下,天线阵接收机可以对每个阵列通道的输出信号分别进行卫星捕获和跟踪处理,其处理过程跟普通单天线接收机相同。
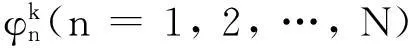

(7)
由于天线阵元间的幅相不一致对接收信号的影响将会体现在载波相位当中,因此即使不对天线阵进行校正,这种方法也能正确估计出信号的导向矢量。
估计得到信号导向矢量后,进一步可以用MVDR算法的原理来进行盲波束形成。盲波束形成算法的输出可表示为:
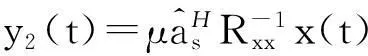
(8)
2.3 输出切换控制
盲零陷形成算法可以在干扰环境下接收机冷启动时正常运行,而盲波束形成算法能在无干扰或弱干扰条件下形成波束使性能更优。两种算法各有优势,因此需通过输出切换控制算法来选择哪一路作为最终的输出。
切换控制可以通过两种算法来实现。第一种算法是增加一个干扰检测模块,当检测到环境中的干扰功率超过一定门限时则选择盲零陷形成算法的输出作为最终输出,否则选择盲波束形成算法。这种切换控制算法实现简单,但可能不是最优的,因为即使当环境中的干扰功率超过门限、单个阵元通道的输出信号无法被捕获跟踪到时,盲波束形成算法仍然可能通过采用前一时刻估计的导向矢量进行波束形成而获得优于盲零陷形成算法的性能。
考虑到载噪比(carrier-to-noise ratio, C/N0)或等效载噪比[14](考虑干扰抑制后存在残余干扰的情况,将残余干扰等效成噪声来处理)将直接决定后端的伪码和载波相位测量精度,因此第二种算法是通过载噪比监测(存在残余干扰时测量得到的是等效载噪比)来完成输出切换。当盲零陷形成算法输出信号的载噪比大于盲波束形成算法输出信号的载噪比时,选择前者作为最终的输出,否则选择后者。
载噪比可以从跟踪环输出的相干积分结果估计得到,目前导航接收机中广泛采用的载噪比估计方法是宽窄带载噪比估计法[15]。假设接收机跟踪环输出的同相和正交相干积分结果分别为IP(n)和QP(n),相关积分时间为T,则在噪声带宽分别为1/T和1/(MT)条件下对应的宽带功率和窄带功率可表示为[15]:

(9)

(10)
将窄带功率用宽带功率进行归一化并求平均,其平均值可表示为:

(11)
式(9)、式(10)、式(11)中的M和K均为正整数,可根据伪码周期和调制数据速率来选取。最终估计的载噪比可用式(12)计算得到:
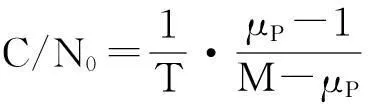
(12)
2.4 算法实现结构
根据上面的推导过程,本文算法总的实现结构可以描述为图2所示。由图可以看出,算法由于增加了大量的跟踪环,其实现复杂度要高于PI算法。但是,一方面,由于跟踪环是导航接收机中一个非常成熟的模块,目前的数字处理器强大的处理能力完全可以使本文算法得以实时实现。另一方面,相对传统的波束形成算法而言,本文算法不需要姿态测量单元辅助,因而其实现代价远远低于传统波束形成算法。
3性能仿真
为验证本文算法的性能,用软件接收机进行了仿真。首先用MATLAB生成阵列信号,用来模拟产生天线阵接收到的不同入射方向上的GNSS信号、干扰以及噪声。然后用本文算法对生成的阵列信号进行处理,并与PI算法以及MVDR算法的处理结果进行对比。基本的仿真参数设置如表1所示。
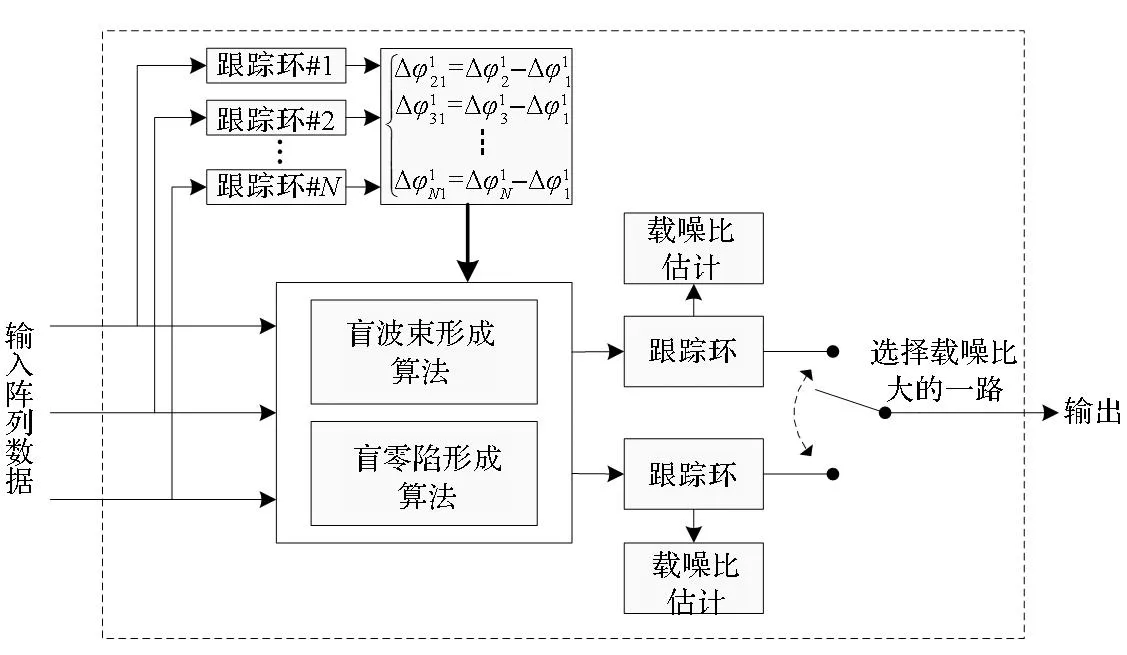
图2 本文算法实现结构Fig.2 Implementation architecture of the proposed algorithm

表1 仿真中用到的参数
3.1 仿真实验一
仿真实验一用于仿真天线阵接收机在干扰条件下冷启动时,各种算法能否正常运行。仿真中,GNSS信号的载噪比设定为42dBHz,干扰1和干扰2一直处于开启状态,分别用本文算法、PI算法以及MVDR算法进行阵列处理,然后对阵列输出信号进行捕获跟踪,并估计载噪比。
图3给出了三种算法处理后得到的信号载噪比。从图中可以看到,在这种条件下,本文算法跟PI算法的性能相同,都能正常捕获跟踪到卫星信号,且载噪比几乎没有损失,而MVDR算法则无法捕获卫星信号(这时也无法正确估计载噪比,图中为方便对比,以30dBHz作为其载噪比结果)。
图4给出了本文算法得到的天线阵增益方向图,图中的圆心位置对应俯仰角90°,圆周边缘对应俯仰角0°。从图中可以看到,天线阵在两个干扰方向(图中用“o”标示其位置)都形成了很深的零陷。这个仿真实验说明采用本文算法的天线阵接收机在干扰条件下冷启动时,可以正常运行并成功捕获跟踪卫星信号。

图3 不同算法对应的信号载噪比Fig.3 Output C/N0 of different algorithms

图4 采用本文算法得到的天线阵增益方向图Fig.4 Gain pattern of antenna array obtained by the proposed algorithm
3.2 仿真实验二
仿真实验二用于仿真各种算法在无干扰时的性能。仿真条件设置如下:整个实验过程中不开启干扰,GNSS信号的初始载噪比设定为42dBHz,且在第2s时,GNSS信号载噪比下降12dB,用来模拟遮挡或其他原因引起的信号衰减。
图5给出了三种算法处理后得到的信号载噪比。从图中可以看到,本文算法与MVDR算法的性能相近,在0~2s时,本文算法获得的载噪比比PI算法高6dB左右,这说明本文算法在信号方向获得了增益。第2s之后,信号衰减了12dB,此时由于信号载噪比太低,PI算法无法继续跟踪上信号,跟踪环失锁(图中为方便对比,以30dBHz作为其载噪比结果),而本文算法由于利用天线阵将信号增强了6dB,仍然可以继续跟踪信号。

图5 不同算法对应的信号载噪比Fig.5 Output C/N0 of different algorithms
图6给出了本文算法得到的天线阵增益方向图,从图中可以看到,天线阵在信号方向(图中用“x”标示其位置)形成了波束。这个仿真实验说明采用本文算法的天线阵接收机在无干扰条件下可以形成波束来增强卫星信号,从而提高卫星的可见性以及定位精度。

图6 采用本文算法得到的天线阵增益方向图Fig.6 Gain pattern of antenna array obtained by the proposed algorithm
3.3 仿真实验三
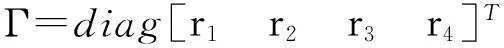
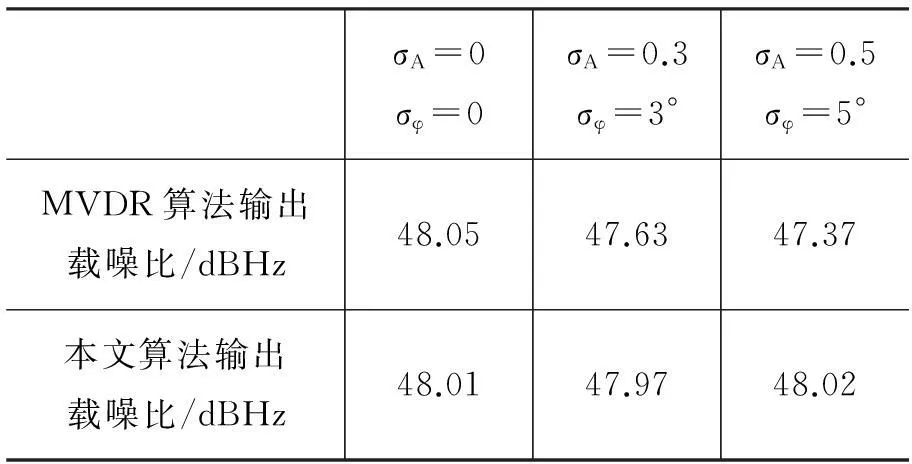
表2 不同算法得到的载噪比
从表2中可以看出随着阵元幅相不一致性增大,MVDR算法的载噪比损耗越大,而本文算法的载噪比基本不变。这是因为阵元幅相不一致引起了导向矢量误差,导致MVDR算法形成的波束指向偏离了真实的卫星方向。而本文算法采用的是载波相位来估计导向矢量,由于阵元幅相不一致对导向矢量的影响将会体现在载波相位当中,因此该算法仍能将波束正确指向卫星方向,对幅相不一致引起的导向矢量误差不敏感。
4结论
载波相位辅助的GNSS天线阵抗干扰算法集成了盲零陷形成和盲波束形成两者各自的优点,在干扰环境且接收机冷启动的条件下仍能成功抑制干扰、正常运行,且在无干扰或弱干扰条件下能进行波束形成来增强卫星信号,从而提高卫星的可见性以及定位精度。在仿真实验中,采用了与定位性能直接相关的输出信号载噪比来评估算法的性能。仿真结果表明该算法的性能明显优于PI算法,且非常接近MVDR算法(在干扰环境下冷启动时甚至还要优于MVDR算法)。该算法不需要先验信息辅助,其实现代价远小于MVDR算法,具有一定的应用价值。需要指出的是,对于提到的根据一定门限来进行输出切换控制,还没有给出最优的门限值,而这是算法工程实现必须解决的问题,有关这方面的问题,将作进一步研究。
参考文献(References)
[1]Daneshmand S, Broumandan A, Lachapelle G.GNSS interference and multipath suppression using array antenna[C]//Proceedings of the 24th International Technical Meeting of the Institute of Navigation, Portland, OR, USA, 2011: 1183-1192.
[2]Seco-Granados G, Fernandez-Rubio J A, Fernandez-Prades C. ML estimator and hybrid beamformer for multipath and interference mitigation in GNSS receivers [J]. IEEE Transactions on Signal Processing, 2005, 53(3):1194-1208.
[3]O’Brien A J. Adaptive antenna arrays for precision GNSS receivers [D]. Columbus,USA: the Ohio State University, 2009.
[4]Arribas J, Fernandez-Prades C, Closas P. Antenna array based GNSS signal acquisition for interference mitigation [J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 223-243.
[5]LI M, Dempster A G, Balaei A T, et al. Switchable beam steering/null steering algorithm for CW interference mitigation in GPS C/A code receivers [J]. IEEE Transactions on Aerospace and Electronics Systems, 2011, 47(3):1564-1579.
[6]Zhang Y D, Amin M G. Anti-jamming GPS receiver with reduced phase distortions [J]. IEEE Signal Processing Letters, 2012, 19(10): 635-638.
[7]Frost O L Ⅲ. An algorithm for linearly constrained adaptive array processing [J]. Proceeding of IEEE, 1962, 60(8): 926-935.
[8]Applebaum S P. Adaptive arrays [J]. IEEE Transaction on Antennas and Propagation, 1976, 24(5): 585-598.
[9]桑怀胜, 李峥嵘, 王飞雪, 等. 采用RLS算法的功率倒置阵列的性能 [J]. 国防科技大学学报, 2003, 25(3): 36-40.
SANG Huaisheng, LI Zhengrong, WANG Feixue, et al. The performance of power inversion array using RLS algorithm[J]. Journal of National University of Defense Technology, 2003, 25(3): 36-40.(in Chinese)
[10]Compton R T, Jr. The power-inversion adaptive array: concept and performance [J]. IEEE Transactions on Aerospace and Electronic Systems, 1979, AES-15(6): 803-813.
[11]Chen Y H, Juang J C, Seo J,et al. Design and implementation of real-time software radio for anti-interference GPS/WAAS sensors [J]. Sensors, 2012,12(10):13417-13440.
[12]Chen Y H, Juang J C,De Lorenzo D S, et al. Real-time software receiver for GPS controlled reception pattern antenna array processing [C]// Proceedings of the 23th International Technical Meeting of the Institute of Navigation, Portland, OR, USA, 2010:1932-1941.
[13]Daneshmand S, Sokhandan N, Zaeri-Amirani M,et al. Precise calibration of a GNSS antenna array for adaptive beamforming applications [J]. Sensors, 2014, 14(6):9669-9691.
[14]Kaplan E D, Hegarty C J. Understanding GPS: principles and applications [M]. 2nd ed. Norwood, MA,USA: Artech House, 2006.
[15]谢钢. GPS原理与接收机设计[M]. 北京:电子工业出版社, 2009.
XIE Gang. Principles of GPS and receiver design [M]. Beijing: Publishing House of Electronics Industry, 2009. (in Chinese)
[16]王永良, 吴仁彪. 通道不一致性、互耦对最优阵列处理器的影响 [J]. 系统工程与电子技术, 1993,15(2): 49-55.
WANG Yongliang,WU Renbiao. Effect of channel-to-channel mismatch and mutual-coupling on the performance of optimum array processors [J]. Systems Engineering and Electronics, 1993, 15(2): 49-55.(in Chinese)
http://journal.nudt.edu.cn
Anti-jamming algorithm for GNSS antenna array aided by carrier phase
CHENFeiqiang,NIEJunwei,SUYingxue,WANGFeixue
(College of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)
Abstract:An anti-jamming algorithm for satellite navigation antenna array aided by carrier phase was proposed to mitigate the interference of satellite navigation receiver. The blind null steering was achieved through the algorithm and the blind beam steering was realized simultaneously with the aid of the carrier phase of the output signal from each individual antenna, and two steerings could be switched by a control algorithm. The simulation results show that the proposed algorithm performs well at “cold” start when the receiver is initiated in strong interference conditions. It can enhance the satellite signals by steering beams to the satellites under noninterference or weak interference conditions, so the visibility and positioning accuracy of satellite are improved. The proposed algorithm can work normally without the aid of inertial measurement unit, and is robust to the steering vector errors caused by amplitude-phase mismatch. It has less cost than traditional beamforming algorithms for implementation.
Key words:satellite navigation; beamforming; antenna array; anti-jamming; power inversion; carrier phase
中图分类号:TN967.1
文献标志码:A
文章编号:1001-2486(2015)06-069-05
作者简介:陈飞强(1988—),男,湖南益阳人,博士研究生,E-mail:matlabfly@hotmail.com;王飞雪(通信作者),男,教授,博士,博士生导师,E-mail:wangfeixue365@sina.com
基金项目:国家自然科学基金资助项目(61371158,61071140)
收稿日期:*2015-04-18
doi:10.11887/j.cn.201506014

