具有潜在索赔的风险模型在重尾赔付下的极限性质

肖鸿民,赵　婕,宋国龙

(西北师范大学数学与统计学院,甘肃兰州　730070)

具有潜在索赔的风险模型在重尾赔付下的极限性质

肖鸿民,赵婕,宋国龙

(西北师范大学数学与统计学院,甘肃兰州730070)

摘要：研究一类带有潜在索赔的风险模型.假设索赔额序列是独立同分布的重尾随机变量序列,不同保单发生实际索赔的概率不同.当潜在索赔额序列服从S族时,得到了有限时间破产概率的渐近表达式.

关键词：有限时间破产概率；独立随机变量；S族；潜在索赔；更新过程

0引言

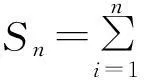
N(t)=sup{n≥1:Sn≤t},t≥0.

保险资本的盈余过程定义为

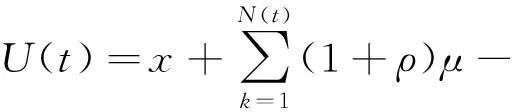
(1)

这里x是初始资金,μ是索赔额均值,常数ρ(ρ>0)为安全负载系数,每张保单的保费为(1+ρ)μ;Xk是第k个客户的潜在索赔额，对每一个k≥1,Bernonlli随机变量Ik表示第k份保单是否发生索赔,Ik=1表示发生索赔.设{Xn,n≥1}是同分布的随机Weibull变量,索赔过程N(t)是参数λ=2的齐次Possion过程,当初始资金x=10 000,T=100时,我们得到了盈余过程的样本轨道,见图1.

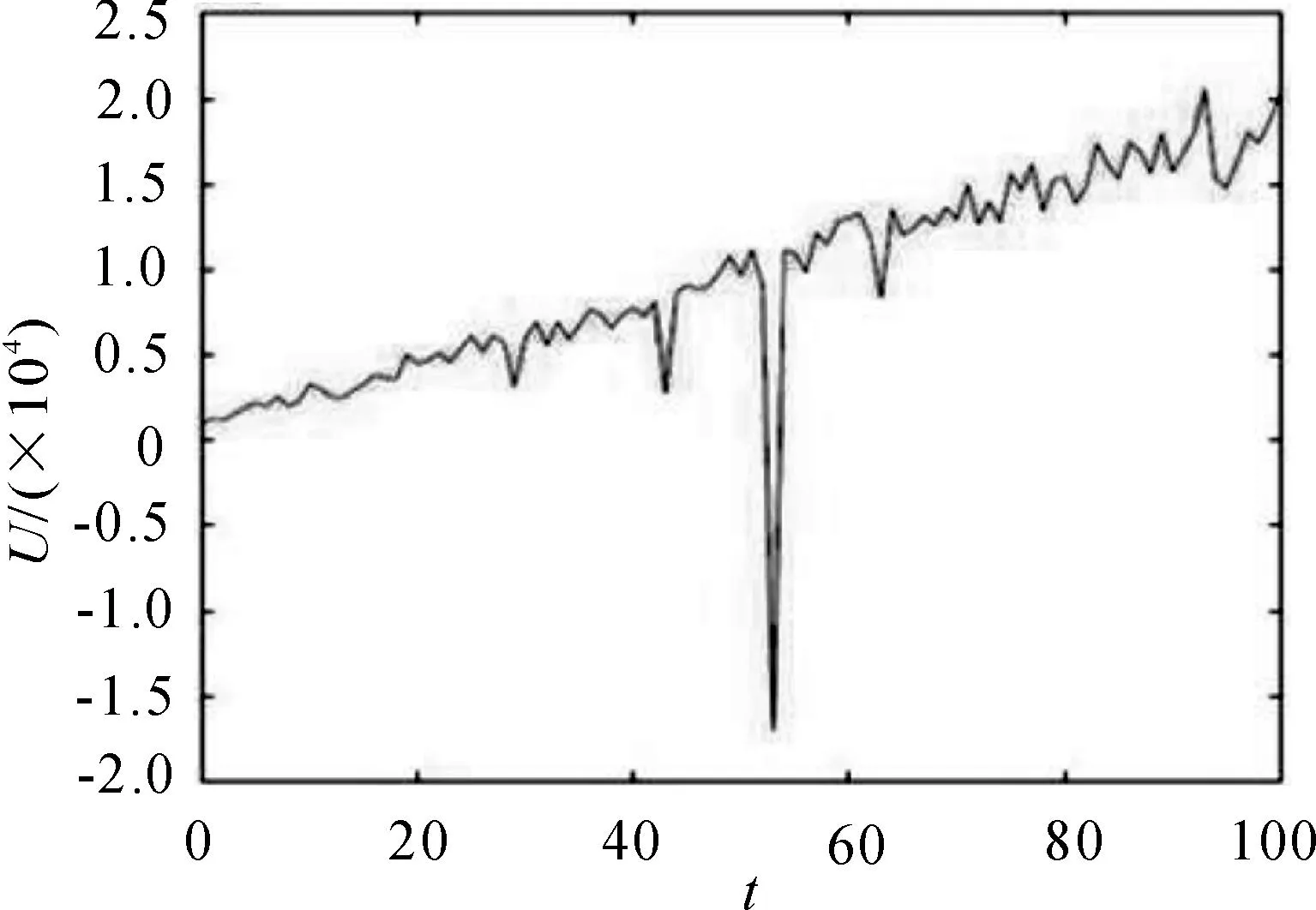
图1　盈余过程的样本轨道

上述模型由文献[4]首次提出后，已经取得了丰富的研究结果.文献[4]研究了该模型当潜在索赔额Xk是独立同分布的ERV族随机变量序列时,损失过程的精细大偏差；索赔额序列是负相关随机变量且具有更一般的控制变化的尾情形下的研究结果参见文献[5]；当{N(t):t≥0}为复合二项过程F∈ERV时,损失过程的精细大偏差可参见文献[6],作者进一步得到了重尾索赔下有限时间破产概率的渐近性质.文献[7]研究了当{N(t):t≥0}为一般更新计数过程,而潜在索赔额{xk}是负相依的L∩D族随机变量序列时,破产概率的渐近表达式.本文放宽了文献[7]的条件，将所讨论的分布扩大到S族,得到了潜在索赔额风险模型的有限时间破产概率.

1预备知识

首先定义直到时刻T的有限时间破产概率为

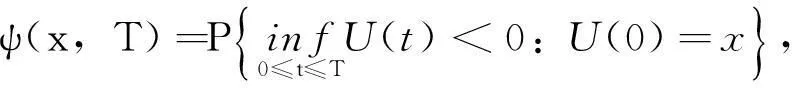
(2)

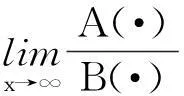
定义1称一个分布F属于L族,如果对任意固定的y(或等价地对y=1),F满足

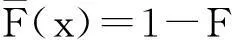
定义2称一个分布F属于S族,如果F满足

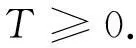
对于某个n≥2(或等价地对任意的n≥2),即

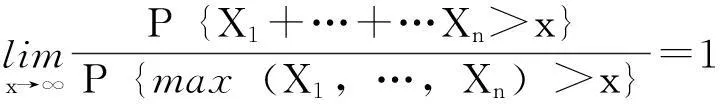
易知,上述重尾分布族具有如下关系:

S⊂L.

本文需要以下假设：

(K1)更新计数过程{N(t):t≥0}具有有限的均值函数m(t)=E[N(t)].

(K2){Ik:k≥1}是相互独立的Bernonlli随机变量序列,P(Ik=1)=θk;P(Ik=0)=1-θk,且存在θ>0,使得

(K3)索赔额{Xk:k≥1}是独立的非负随机变量序列,有共同的分布F,且F∈S族,均值μ<∞.

(K4)随机变量族{Xk:k≥1},{Ik:k≥1},{N(t):t≥0}相互独立.

引理1[8]如果F∈S族,那么对任意的ε>0,存在C(ε)>0,使得下列式子对所有的n=1,2,…和x≥0,一致地有

注1当{Ik:k≥1}同分布时，由S族的定义知{IkXk:k≥1}的分布属于S,并且有{IkXk-(1+ρ)μ:k≥1}的分布属于S.

引理2[9]在条件(K1)~(K4)下,对任意给定的正整数n,我们有

(3)

证明见文献[9]命题5.1.

2主要结果及证明

定理1对模型(1),在条件(K1)~(K4)下,直到时刻T的有限时间破产概率满足

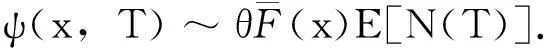
(4)

证明由盈余过程的表达式(1),对每个t∈(0,T],有

根据有限时间破产概率的定义,我们有

且对于某个0≤t≤T,有

类似地有

所以,如果证明了

那么就证明了

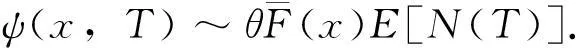
选择任意正整数N,对于t∈(0,T],有

首先考虑J2(x,t,N).由引理2可得

因此

对J1(x,t,N),有

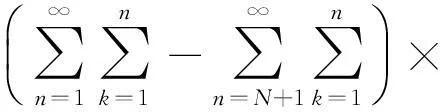
因为

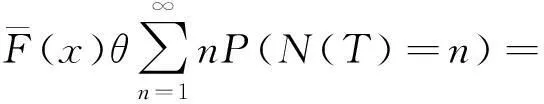
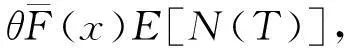
又因为

而对所有x,有

所以

下证

因为{IkXk-(1+ρ)μ:k≥1}∈L,则有

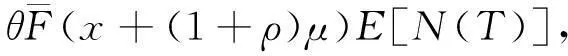
所以

定理得证.】

从而，当潜在索赔额序列服从S族时,我们得到了有限时间破产概率的渐近表达式.

参考文献:

[1]EMBRECHTSP,KLUPPELBERGC,MIKOSCHT.Modelling Extremal Events for Insurance and Finance[M].Berlin:Springer,1997.

[2]GOLDIECM,KLUPPELBERGC.Subexponential Distributions:A Practical Guide to Heavy Tails:Statistical Techniques for Analysing Heavy Tailed Distributions[M].Boston:Birkhauser,1998.

[3]ROLSKIT,SCHMIDLIH,SCHMIDTV,etal.Stochastic Processes for Insurance and Finance[M].Chichester:JohnWileySons,1999.

[4]NGKW,TANGQH,YANJA,etal.Preciselargedeviationsfortheprospective-lossprocess[J].Appl Prob,2003,40:391-400.

[5]WANGYB,WANGKY,CHENGDY.Preciselargedeviationsforsumsofnegativelyassociatedrandomvariableswithcommondominatedlyvaryingtails[J].Acta Mathematica Sinica (EnglishSeries),2006,22(6):1725-1734.

[6]马学敏,胡亦钧.复合二项过程风险模型的精细大偏差及有限时间破产概率[J].数学学报,2008,51(6):1119-1130.

[7]肖鸿民,刘建霞.带负相依重尾潜在索赔额的风险模型的有限时间破产概率[J].山东大学学报:理学版,2011,46(9):117-121.

[8]江涛.常息力更新场合有限时间破产概率对负相依索赔额的不敏感性[J].高校应用数学学报:A辑,2009,24(4):401-409.

[9]TANGQi-he,TSITSIASHVILIG.Randomlyweightedsumsofsubexponentialrandomvariableswithapplicationtoruintheory[J].Extremes,2003,6(3):171-188.

(责任编辑马宇鸿)

E-mail:xiaohm9@126.com

Thelimitpropertiesforariskmodel

withheavy-tailedpotentialclaims

XIAOHong-min,ZHAOJie,SONGGuo-long

(CollegeofMathematicsandStatistics,NorthwestNormalUniversity,Lanzhou730070,Gansu，China)

Abstract:In this paper a risk model with prospective-claim is studied,in which the customers’ potential claims are heavy-tailed random variables with independent identically distribution.Different insurance policy holders are allowed to have different probabilities to make actual claims.When customers’ potential claims belong to class S,an asymptotic expression of the finite-time ruin probability is derived.

Key words:finite-time ruin probability;independent random variables;class S;prospective-claim;renewal process

中图分类号：O 211.4

文献标志码：A

文章编号：1001-988Ⅹ(2015)02-0009-03

作者简介：肖鸿民(1967—),女,甘肃临洮人,教授,博士.主要研究方向为概率极限理论与保险数学.

基金项目:国家自然科学基金资助项目(71261023)

收稿日期：2014-03-23;修改稿收到日期:2014-12-22