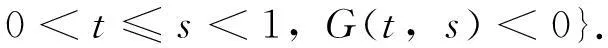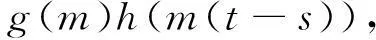一类非共轭边值问题Green函数定号的最优区间

李　辉，冯育强*，布昶昶

(武汉科技大学理学院，湖北武汉　430065)

一类非共轭边值问题Green函数定号的最优区间

李辉，冯育强*，布昶昶

(武汉科技大学理学院，湖北武汉430065)

摘要：证明了一类非共轭微分方程在非共轭边值条件下Green函数定号的最优区间的存在性，使得当参数在此最优区间时,Green函数是定负的.随后用逆向搜索法找到参数最优区间的左、右端点.

关键词：Green函数；定号；最优区间；三阶微分方程

0引言

三阶微分方程边值问题因其在电磁波和重力驱动流以及三层梁[1]等研究中的重要应用，近年来引起了许多学者的关注.关于三阶微分方程边值问题的研究已经出现了很多理论和方法，如：微分不等式方法[2,3]、非共轭性理论[4,5]、不动点方法[6]、变分方法[7]、拓扑度理论以及解的先验界估计[8]、上下解方法[9],等等.

在讨论三阶微分方程边值问题解的存在性、唯一性及其它性质时，Green函数有着非常重要的作用：利用Green函数，可以将微分方程的求解问题转化为积分方程求解.Torres[6]曾用自伴算子的谱理论得到了二阶微分方程的周期边值问题Green函数定号的条件.马如云[5]用非共轭性理论讨论了非自伴算子三阶微分方程的共轭边值问题，得到了一个关于原点对称的Green函数定号的最优区间，但用非共轭性理论去解决非共轭边值条件时上述理论完全失效.本文讨论非自伴算子的三阶微分方程非共轭边值问题，首先证明该最优区间的存在性，然后用逆向搜索法得到了Green函数定号的最优区间.

1预备知识

定义1[10]令pk∈C[a,b]，k=1,…,n.如果一个n阶线性微分方程

的任意非平凡解在区间[a,b]上有少于n个零点，那么该方程在区间[a,b]上被称为是非共轭的，其中多重零点按重数计算.

定义2[5]对于三阶微分方程

的(k,3-k)共轭边值条件(这里k=1,2)，仅有下面两种情形：

1)u∈{v∈C3[0,1]:v(0)=v′(0)=v(1)=0};

2)u∈{v∈C3[0,1]:v(0)=v(1)=v′(1)=0}.

本文将讨论非共轭边值条件的情形，即

2Green函数的计算

引理1设M=m3，考察边值问题

(i)当m≠0时，该问题的Green函数为

其中

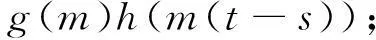
(ii)当m=0时，该问题的Green函数为

证明( i )当m≠0时，对应的齐次微分方程的基础解系为

设非齐次线性方程的特解为

利用常数变易法解得

故其特解为

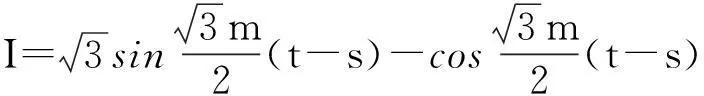
由边值条件u(0)=u′(0)=u′(1)=0，可解得c1,c2,c3，代入经过化简，即得Green函数为

( ii )当m=0而0≤s≤t≤1时,因为

所以

将Ft,s(m),g(m)在m=0处泰勒展开，得到

所以

同理可得当0≤t≤s≤1时,

所以

这个结果恰和文献[10]的结果相符.】

注1对0≤s≤t≤1情形，由于s=0或t=s=1时G(t,s)=0.而0≤t≤s≤1情形，由于t=0或t=s=1时，G(t,s)=0，所以以下讨论G(t,s)的符号时约定t,s∈(0,1).

3Green函数的最优区间讨论

引理2当m<0时，有g(m)<0,h(m)>0.

推论1当m<0且0

引理3存在α<0,β>0,满足：

(1)当m∈(α,0)时，对∀0

(2)当m∈(0,β)时，对∀0

(3)当m=0时，G(t,s)<0.

证明(1)当m∈(α,0)时,对∀0

所以有

故存在α<0，当m∈(α,0)时，对∀00.

(2)当m>0时，由前面的计算可知

故存在β>0，当m∈(0,β)时，对∀0

(3)当m=0时，

由于当0

设

则由引理3知T0≠∅,T1≠∅.

引理4T0,T1是有界集.

证明取m1=-4.3,s1=0.004,t1=0.946，则有

故m1∉T0.即知T0以m1为下界.

又当m2=3.1,s2=10-3,t2=10-3时，有

故m2∉T1.即知T1以m2为上界.】

定义

易知T2≠∅.设

引理5设函数

的最小正零点为m=λ,而函数

的最小正零点为m=μ,则当m>0时，

(1)对∀0

(2)对∀0

(3)τ=min{τ1,τ2}=τ1.

证明(1) 当0

但是存在s0=1+(θ0-1)λ/τ2,θ0∈(0,1)，使得

因为当τ2(1-s0)<λ，即1-λ/τ20，即有G(t0,s0)>0.这样Green函数就不能定负了，故τ2≤λ<+∞.又由于当m∈(0,λ)时，G(t,s)<0，所以τ2=λ.

(2)当0

所以存在t1=s1=(1-λ/τ1)/10 ，使得

事实上只要τ1(1-s1)>λ，即0

所以

所以τ1≤λ，故τ2≥τ1.

(3)由(1)、(2)可得.】

由引理4、引理5可知

定理1存在一个最优区间(τ0,τ1)，使得当m∈(τ0,τ1)时G(t,s)<0.

4最优区间的近似搜索

算法(逆向搜索法)仅对τ0说明，τ1类似.

在Ft,s(m)中，想要直接找出参数m的最优取值范围(区间的左端点),使得当m∈U-(0;δ)时，对∀00恒成立是困难的，因为一个m值对应一个二元函数.但可以反过来考虑：在m<0的范围内，当给定一个m值，让计算机找一个t值和一个s值，只要找到一对这样的t,s值，使得Ft,s(m)≤0(固定此t和s，这就相当于是关于m的一元函数.根据函数的连续性，在此m值附近的一个充分小领域内的值都是不在此最优区间内的)，此m值及其附近的值都舍弃.因这些值都不在目标区间内，不满足要求.所以只要计算机找不到这样的t值和s值，则给定的m值总是在此最优区间内；若找得到一对t值和s值，则给定的m值总是不在此最优区间内的.按此算法，可先定出τ0的整数部分，然后再依次定出小数点后的十分位﹑百分位、千分位，等.由于计算机内存默认最小浮点运算误差限为2.2204×10-16，所以应避免计算Ft,s(m)值时出现接近于0但又非0的小数，计算机将其视为0而导致错误判断.由引理6，可排除该式子在m∈U-(0;δ)内等于0的可能，故将“Ft,s(m)≤0”改为：“Ft,s(m)<0”进行编程搜索，另外在搜索时可让s的初值和步长均取10-5，终值取0.99999.让t的初值等于s，步长和终值与s相同，然后反复更换m值进行搜索.

为缩小搜索范围，我们可先确定左端点的大致范围，然后再按上述方法做精确搜索.为此可以先让m值从-10到10的范围内以步长0.001进行编程搜索.对于

给定一个m值对应一个二元函数.下面将s,t以小步长离散化，求出每当给定一个m值时对应的二元函数的最小值，并绘制出m随着该二元函数最小值变化的曲线图，得到左端点的图1.

图1　m随二元函数Ft,s(m)的

图2　　m随二元函数Ft,s(m)的

从图1可以看出左端点大约在-4.5到-4之间，并且当m∈(τ0,0)时,Ft,s(m)的最小值都是大于0的，满足要求.但当时最小值就是小于0的.由于s,t是离散的，所以图1显示在-4.5到4之间有间断点出现.

m1=-4.3,s1=0.004,t1=0.946

用同样搜索技巧得到的右端点见图2.从图2可以看出，右端点大约在3到3.5之间，并且当m∈(0,τ1)时Ft,s(m)的最大值都小于0，满足要求.有了大致范围就可用逆向搜索法做精确搜索了.

结论τ0≈-4.2332,τ1≈3.0167.

参考文献:

[1]GREGUS M.ThirdOrderLinearDifferentialEquations[M].Mathematics and Its Applications.Dordrecht：Reidel,1987.

[2]KLAASENG.Differentialinequalitiesandexistencetheoremsforsecondandthirdorderboundaryvalueproblems[J].J Differential Equations,1971,10:529-537.

[3]JACKSONLK.Existenceanduniquenessofsolutionsofboundaryvalueproblemsforthirdorderdifferentialequations[J].J Differential Equations,1973,13:432-437.

[4]FENGYu-qiang,LIUSan-yang.Multiplicityofsolutionsforanonlinearthird-orderboundaryvalueproblem[J].J Engineer Math,2003,20:109-112.

[5]MARu-yun.Disconjugacyandextremalsolutionsofnonlinearthird-orderequations[J].Commun Pur Appl Anal,2014,13:1223-1236.

[6]TORRESPJ.Existenceofone-signedperiodicsolutionsofsomesecond-orderdifferentialequationsviaaKrasnoselskiifixedpointtheorem[J].J Differential Equations,2003,190:643-662.

[7]WARDJRJr.Periodicsolutionsofordinarydifferentialequationswithboundednonlinearities[J]. Topol Method Nonl Anal,2002,19:275-282.

[8]MAWHINJ.Topologicaldegreeandboundaryvalueproblemsfornonlineardifferentialequations[M]//FURIM,ZECCAP.Topological Methods for Ordinary Differential Equations.LectureNotesinMathematicsVol1537.NewYork:Springer,1993:74-142.

[9]CABADAA.Themethodofloweranduppersolutionsforsecond,third,fourthandhigherorderboundaryvalueproblems[J].J Math Anal Appl,1994,185:302-320.

[10]COPPELWA.Disconjugacy[M].LectureNotesinMathematicsVol220.Berlin:Springer,1971.

(责任编辑马宇鸿)

E-mail:675130385@qq.com

*通讯联系人，男，教授.主要研究方向为非线性泛函分析.E-mail:fengyuqiang@wust.edu.cn

The optimal interval for Green’s function having a constant

sign of a non-conjugate boundary value problem

LI Hui,FENG Yu-qiang，BU Chang-chang

(School of Science，Wuhan University of Science and Technology，Wuhan 430065，Hubei，China)

Abstract:The existence of the optimal interval is proved,such that the Green’s function of a disconjugate differential equation with non-conjugate boundary condition will get negative sign when the parameter is in this interval.Then,the left and right endpoints of this interval are found by backward searching method.

Key words:Green’s function;constant sign;optimal interval;third-order differential equation

中图分类号：O 175.08

文献标志码：A

文章编号：1001-988Ⅹ(2015)02-0004-05

作者简介：李辉(1987—)，男，湖北潜江人，硕士研究生.主要研究方向为非线性泛函分析.

基金项目:教育部高等学校博士点基金项目(20134219120003);湖北省自然科学基金重点项目(2013CFA131);冶金工业过程的系统科学湖北省重点实验室基金项目(z201302)