条件(P′)和(E′)的积与余积

王利民，焦天明

(西北师范大学数学与统计学院,甘肃兰州　730070)

条件(P′)和(E′)的积与余积

王利民，焦天明

(西北师范大学数学与统计学院,甘肃兰州730070)

摘要：证明了每一个右S-系Ai满足条件(P′)(条件(E′))当且仅当满足条件(P′)(条件(E′));得到了每一个右S-系 Ai满足条件(P′)(条件(E′))与满足条件(P′)((条件(E′))等价的充分必要条件.

关键词：积;余积;满足条件(P′);条件(E′);对角系

中图分类号：O 152.7

文献标志码：A

文章编号：1001-988Ⅹ(2015)03-0020-03

Productandcoproductforcondition(P′)andcondition(E′)

WANGLi-min，JIAOTian-ming

(CollegeofMathematicsandStatistics,NorthwestNormalUniversity,Lanzhou730070,Gansu,China)

Abstract:This paper proves that every right S-acts Aisatisfies condition (P′)(resp.condition (E′)) if and only if the coproduct satisfies condition (P′)(resp.condition (E′)).It is obtained the characterization of monoids over which every right S-acts Aisatisfies condition(P′)(resp.condition (E′)) if and only if the product satisfies condition (P′)(resp.condition (E′)).

Key words:product;coproduct;conditions (P′);condition (E′);diagonal acts

0引言

设S是幺半群,一个非空集合A称作是右S-系,如果存在一个映射f:A×S→A,(a,s)→as使得对任意的a∈A,s,t∈S,满足(as)t=a(st),1a=a.记作AS.特别地,当A=S×S时,如果定义(s,t)u=(su,tu),那么称右S-系S×S为对角S-系,记作D(S).2009年,Bulman[1]对D(S)的平坦性做了讨论.近些年来,D(S)的性质已经引起了许多学者的关注[2,3].

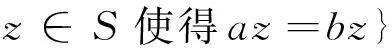
是局部循环S-系.关于(E′)也有类似的结果.

记E(S)为S的幂等元集,一元S-系ΘS为{θ}.再记

文中没有特别说明的概念和记号见文献[8].

1主要结果

定义1[2]对任意的a,a′∈A,s,s′,z∈S,若as=a′s′,sz=s′z,则存在a″∈A,u,v∈S,使得a=a″u,a′=a″v,us=vs′,那么称右S-系AS满足条件(P′).

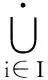
定义2[2]对任意的a∈A,s,s′,z∈S,若as=as′,sz=s′z,则存在a′∈A,u∈S,使得a=a′u,us=us′,那么称右S-系Ai满足条件(E′).

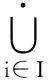
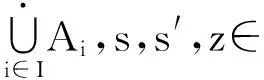
定义3[2]对任意的a,a′∈A,s∈S.若as=a′s,则存在a″∈A,u,v∈S,使得a=a″u,a′=a″v,us=vs.那么称右S-系Ai满足条件(PWP).

命题3设S是幺半群，则以下条件等价:

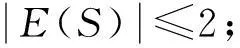
(2)S是右可消的.

证明(1)⟹(2).对任意的a,a′,s∈S，若as=a′s,则(1,a)s=(1,a′)s.因为D(S)满足条件(PWP),所以存在(c,d)∈D(S),使得

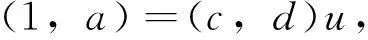
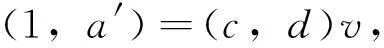
us=vs，

cu=cv=1,

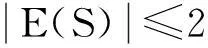
(2)⟹(1).对任意的s∈S,a,b∈D(S)，如果as=bs,那么a=b，从而D(S)满足条件(PWP).】

定理1设S是幺半群，则以下条件等价:

(2){θ}满足条件(E′);

(3)S是弱左collapsible.

(2)⟹(3).对任意的s,s′,z∈S,显然θs=θs′,sz=s′z.因为{θ}满足条件(E′),所以存在u∈S,使得θ=θu,us=us′,故S是弱左collapsible.

(3)⟹(1).对于某个固定的i∈I,任意的ai∈Ai,s,s′,z∈S,假设ais=ais′,sz=s′z,因为S是弱左collapsible,所以存在u1∈S,使得u1s=u1s′.对某个固定的j,aj∈Aj,如果定义

定理2设S是幺半群，则以下条件等价:

(2){θ}满足条件(P′);

(3)S是弱右reversible.

(2)⟹(3).对任意的s,s′,z∈S,显然θs=θs′,sz=s′z.因为{θ}满足条件(P′),所以存在u,v∈S,使得θ=θu,us=vs′,故S是弱右reversible.

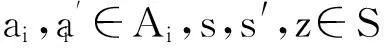
即Ai满足条件(P′).】

定义4[1]若AS的由两个元素生成的任意子系包含在AS的一个循环子系中,则称AS是局部循环的.类似地有局部循环主理想的概念.

定理3设S是幺半群，则以下条件等价:

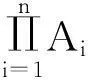
(2)D(S)满足条件(E′);

(3)对于任意的a,b∈S,非空集合lz(a,b)是S的局部循环主左理想.

证明(1)⟹(2).显然.

(2)⟹(3).假设D(S)满足条件(E′),任意的a,b∈lz(s,t),其中s,t∈S，则由as=bt,bs=bt可得(a,b)s=(a,b)t,sz=tz.因为D(S)满足条件(E′),所以一定存在(c,d)∈D(S),使得(a,b)=(c,d)u,us=ut.所以存在u∈S使得a,b∈Su⊆lz(s,t).即lz(a,b)是S的局部循环主左理想.

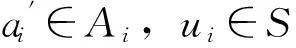
us=us′.

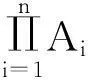
定理4设S是幺半群，则以下条件等价:

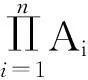
(2)对角系D(S)满足条件(P′);

(3)对于任意的a,b∈S,非空集合Lz(a,b)是S的局部循环S-系.

证明(1)⟹(2).显然.

(2)⟹(3).假设D(S)满足条件(P′),对任意的(a,b),(a′,b′)∈Lz(s,t),其中s,t∈S，有as=bt,a′s=b′t,从而(a,a′)s=(b,b′)t,sz=tz.因为对角系D(S)满足条件(P′),所以存在(a″,b″)∈D(S),u,v∈S,使得(a,a′)=(a″,b″)u,(b,b′)=(a″,b″)v,us=vt,所以(a,a′),(b,b′)∈S(u,v)⊆Lz(s,t).即Lz(s,t)是局部循环的.

us=us′.

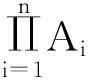
参考文献:

[1]BULMANF.Flatpropertiesofdiagonalactsovermonoids[J].Semigroup Forum,2009,79(2):298-314.

[2]GOLCHINA,MOHAMMADZADEHH.Oncondition(P′)[J].Semigroup Forum,2013,86(2):413-430.

[3]SEDAGHATJOOM,LAANV,ERSHADM.Principallyweakflatnessandregularityofdiagonalacts[J].Comm Algebra,2012,40(11):4019-4030.

[4]SEDAGHATJOOM,KHOSRAVIR,ERSHADM.Principallyweaklyandweaklycoherentmonoids[J].Comm Algebra,2009,37(2):4281-4295.

[5]QIAOHu-sheng.Somenewcharacterizationsofrightcancellativemonoidsbycondition(PWP)[J].Semigroup Forum,2005,71(1):134-139.

[6]GOLCHINA,MOHAMMADZADEHH.Oncondition(EP)[J].International Math Forum,2007,2(17-20):911-918.

[7]ZAREA,GOLCHINA,MOHAMMADZADEHH.Stronglytorsionfreeactsovermonoids[J].Asian-European Journal Mathematics,2013,6(3):1-22.

[8]EILPM,KNAUERU,MIKBALEVA.Monoid,Acts and Categories[M].NewYork,Berlin:WalterGruyter,2000.

(责任编辑马宇鸿)

作者简介：王利民(1950—),男,陕西子洲人,教授，博士研究生导师.主要研究方向为半群代数理论.

收稿日期：2014-11-25;修改稿收到日期:2015-01-09

E-mail:wanglm@nwnu.edu.cn;151931@163.com