双时滞Mackey-Glass系统的稳定性和Hopf分支

杨纪华，马　旭，张二丽，李艳秋

(1.宁夏师范学院数学与计算机科学学院，宁夏固原　756000；

2.郑州财经学院计算机系，河南郑州　450000；

3.南京工业大学理学院，江苏南京　211800)

双时滞Mackey-Glass系统的稳定性和Hopf分支

杨纪华1，马旭1，张二丽2，李艳秋3

(1.宁夏师范学院数学与计算机科学学院，宁夏固原756000；

2.郑州财经学院计算机系，河南郑州450000；

3.南京工业大学理学院，江苏南京211800)

摘要：研究了具有双时滞的Mackey-Glass系统的稳定性与Hopf分支.从系统线性化方程的特征方程根的分布入手，分别研究了单时滞和双时滞Mackey-Glass系统的线性稳定性.当系统中的时滞经过一系列临界值时，系统经历了Hopf分支，并且当时滞较大时，系统出现了混沌吸引子.然后，利用中心流形理论和规范型方法分析了分支周期解的稳定性和Hopf分支的分支方向.最后，数值模拟验证了理论分析结果.

关键词：Mackey-Glass系统；双时滞；稳定性；Hopf分支；混沌吸引子

中图分类号：O 175.13

文献标志码：A

文章编号：1001-988Ⅹ(2015)03-0007-07

Stability and Hopf bifurcation

of Mackey-Glass system with two time delays

YANG Ji-hua1，MA Xu1，ZHANG Er-li2，LI Yan-qiu3

(1.Department of Mathematics and Computer Science,Ningxia Normal University,Guyuan 756000,Ningxia,China;

2.Department of Computer Science,Zhengzhou Institute of Finance and Economics,Zhengzhou 450000,Henan,China;

3.Department of Science,Nanjing University of Technology,Nanjing 211800,Jiangsu,China)

Abstract:The stability and Hopf bifurcation of Mackey-Glass system with two time delays are studied.The linear stabilities with one delay and two delays are investigated,respectively.It is found that Hopf bifurcations exist when the delays pass through a sequence of critical values,furthermore,the system appears chaotic attractors with large time delays.Then,using the center manifold theorem and the normal form method,the direction and stability of the Hopf bifurcation are determined.In the end,some numerical simulations are carried out for supporting the analytic results.

Key words:Mackey-Glass system;two time delays;stability;Hopf bifurcation;chaos attractor

分支现象常常出现在依赖参数的非线性动力系统中.当参数变化时，解的定性结构将发生变化.将平衡点与周期解联系在一起的这种分支对于连续动力系统称之为Hopf分支，对于离散动力系统出现的不变闭曲线称之为Neimark-Sacker分支.关于常微分方程或时滞微分方程的Hopf分支的讨论，已有一些结果[1-3].文献[4]研究了时滞Mackey-Glass系统

(1)

其中，x(t)表示血液循环中成熟细胞的质量分数;τ表示在骨髓中产生未成熟细胞和血流释放成熟细胞的时滞参数;a为系统的反馈率;k,n为正常数.作者应用Trapezoidal方法[5]离散化系统(1)，分析了该离散化系统平衡点的稳定性和Neimark-Sacker分支的存在性，利用中心流形定理和规范型理论讨论了Neimark-Sacker分支的稳定性与分支方向.汪芙平等[6]以间歇驱动方式实现了Mackey-Glass系统的同步，并把它与离散数字传输相结合构成一种新的混沌通信方案.崔万照等[7]根据混沌动力系统的相空间延迟坐标重构理论，基于支持向量机的非线性映射能力，建立了Mackey-Glass混沌时间序列的预测模型.

本文研究双时滞Mackey-Glass系统

(2)

其中，x(t)表示血液循环中成熟细胞的质量分数；τ1和τ2表示在骨髓中产生未成熟细胞和血流释放成熟细胞的时滞参数；k是用于驱动x(t)的松弛系数；a和b是系统的反馈率；n是正常数.该模型的参数必须通过与造血相关的实验数据来确定,其详细的生物学意义可见文献[8-10].本文从稳定性与分支的角度研究具双时滞Mackey-Glass系统，对系统平衡点的稳定性和Hopf分支进行分析．

1平衡点的稳定性和Hopf分支的存在性

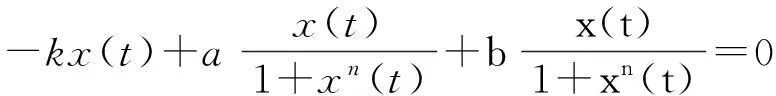
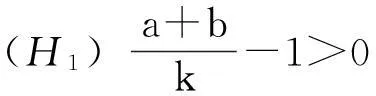
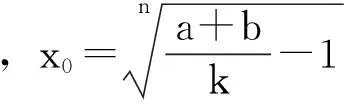
(3)

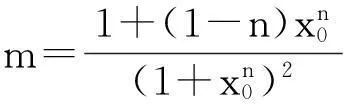
由于具有多重时滞微分方程的动力学性质非常复杂，因此我们先讨论当τ1=0的情况，然后再讨论τ1≠0的情况.

1.1τ1=0的情形

为了讨论方便，我们做如下假设：

引理1( i ) 如果(H2)或者(H3)成立，则当τ2>0时，方程(3)的所有根具有负实部.

(ii) 如果(H4)或者(H5)成立，则当τ=τ2,j时，方程(3)有一对简单纯虚根±iβ0;且当τ2∈[0,τ2,0)时，方程(3)的所有根具有负实部，其中

证明λ=iβ(β>0)是方程(3)的根的充分必要条件是β满足

平方相加可得

(4)

进而可得

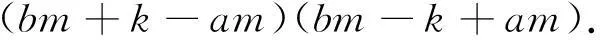
因为k>(a+b)m，所以bm-k+am<0.

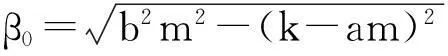
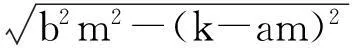
则(τ2,j,β0)是方程(3)的解，即λ=±iβ0是τ2=τ2,j时方程(3)的一对纯虚根.

当τ2>0时，τ2,0是使得方程(3)有根出现在虚轴上的第一个值，由文献[11]中的推论2.4可得，当τ2∈[0,τ2,0)时，方程(3)的所有根具有负实部.】

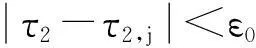
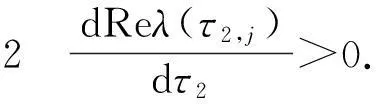
证明方程(3)两端同时关于τ2求导可得

所以

进而可得

定理1(i) 当τ1=0时，如果(H2)或者(H3)成立，则当τ2>0时，系统(2)的平衡点x0是局部渐近稳定的.

(ii)当τ1=0时，如果(H4)或者(H5)成立，则当τ2∈[0,τ2,0)时，系统(1)的平衡点x0是局部渐近稳定的；当τ2∈[τ2,0,+∞)时，系统(2)的平衡点x0是不稳定的,而且当τ2=τ2,j(j=0,1,2…)时，系统(2)经历了Hopf分支，其中τ2,j由引理1所定义.

证明由引理1可得到(i)正确.由引理2可得，当τ2∈[τ2,0,+∞)时，方程(3)至少有一对具有严格正实部的根，所以当τ2∈[0,τ2,0)时，系统(2)的平衡点x0是局部渐近稳定的；当τ2∈[τ2,0,+∞)时，系统(2)的平衡点x0是不稳定的.由文献[12]中关于泛函微分方程的Hopf分支定理可得(ii)正确.】

1.2τ≠0时的情形

固定τ2，以τ1为参数，且τ2取值于使得方程(4)的根都具有负实部的区间.记

g(ω)=k2-2kbmcosτ2ω+

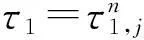
证明设iω(ω>0)是方程(3)的根，则

(5)

所以

k2-2kbmcosτ2ω+2ω bmsinτ2ω+

(6)

由假设可得方程的正根为{ω1,ω2,…,ωs}.令

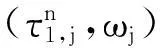
定义

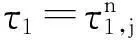
引理4如果ω0τ2cosω0τ1,0+(1+kτ2)sinω0τ1,0≠0，则

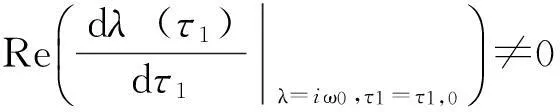
证明方程(3)两端同时关于τ1求导可得

所以

其中

因为ω0τ2cosω0τ1,0+(1+kτ2)sinω0τ1,0≠0，所以

由引理1～4及文献[12]第11章的定理1.1，可以得到下面关于系统(2)的平衡点的稳定性与Hopf分支的存在性定理.

定理2假设(H1)成立,

( i )如果(H2)或者(H3)成立，且g(ω)没有正根，则系统(2)的平衡点是局部渐近稳定的；如果(H2)或者(H3)成立，且g(ω)有正根，则当τ1∈[0,τ1,0)时，系统(2)的平衡点是局部渐近稳定的.在后一种情况中，如果ω0τ2cosω0τ1,0+(1+kτ2)sinω0τ1,0≠0，则当τ1=τ1,0时，系统(2)经历了Hopf分支.

( ii )如果(H4)或者(H5)成立,τ2∈[0,τ2,0)，且g(ω)没有正根，则当τ1≥0时，系统(2)的平衡点是局部渐近稳定的；如果(H4)或者(H5)成立，τ2∈[0,τ2,0)，且g(ω)有正根，则当τ1∈[0,τ1,0)时，系统(2)的平衡点是局部渐近稳定的.在后一种情况，如果ω0τ2cosω0τ1,0+(1+kτ2)sinω0τ1,0≠0，则当τ1=τ1,0时，系统(2)经历了Hopf分支.

2Hopf分支的分支方向和稳定性

本文第1节得到了系统(2)在平衡点经历Hopf分支的一些充分条件，本节研究Hopf分支的性质，即Hopf分支的分支方向和稳定性.我们总假设ω0τ2cosω0τ1,0+(1+kτ2)sinω0τ1,0≠0.

首先对系统(2)采用尺度变换t→t/τ1，可得

(7)

系统(7)在平衡点0处的线性化方程为

(8)

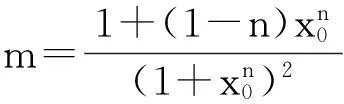
这里

方程(8)的特征方程为

(9)

比较方程(3)与方程(9)可得υ=τ1λ，因此当τ1=τ1,0时，方程(9)有一对纯虚根±iτ1,0ω0.令τ1=τ1,0+μ，则μ=0是系统(2)的Hopf分支值.

记C=C([-1,0],R)，对于φ∈C，令

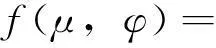
由Risze表示定理，存在函数η(θ,μ)(-1≤θ≤0)，使得当φ∈C时,有

对φ∈C1([-1,0],R)，定义

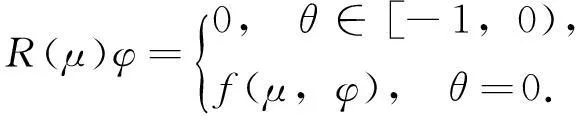
(10)

于是，方程(2)可表示

(11)

其中u(t)=x(t),ut=u(t+θ),θ∈[-1,0],对ψ∈C1[0,1],R)，定义

对于φ∈C1([-1,0],R)和ψ∈C1([0,1],R),定义双线性形式

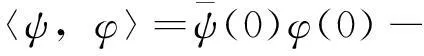
其中η(θ)=η(θ,0),A*和A(0)是伴随算子.

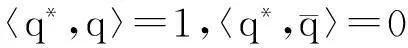
设ut是方程(7)当μ=0时的解，定义z(t)=〈q*(θ),ut,w(t,θ)=ut(θ)-2Re{z(t)q(θ)},则在中心流形C0上有

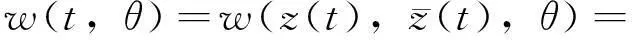
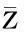
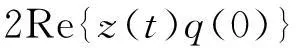
(12)

将其记为

(13)

其中

(14)

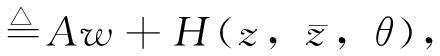
(15)

其中

(16)

比较(15)式两端的系数可得

(17)

由w(t,θ)=ut(θ)-2Re{z(t)q(θ)}可得

又因为

因此有

(18)

比较(14)和(18)式的系数可得

(19)

所以要求出g21，只需求出w11(-1),w20(-1),w11(-τ2/τ1)和w20(-τ2/τ1)即可.

当θ∈[-1,0]时，由(19)式可得

与(16)式比较系数可得

进而可得

所以

再由(17)式可得Aw20(0)=2iω0τ1,0w20(0)-H20(0),Aw11(0)=-H11(0)，因此由A的定义可得

由前面的分析可知，g20,g11,g02和g21都可由系统(2)中参数所确定.因此可以计算出下列值

定理3( i ) 当τ=τ1,0时，系统(1)经历了Hopf分支，且当μ2>0时，Hopf分支是上临界的，当μ2<0时，Hopf分支是下临界的；

( ii )当β2>0时，分支周期解是不稳定的，当β2<0时，分支周期解是稳定的.

3数值模拟

在系统(1)中取k=0.5,a=0.2,b=2,n=10,τ1=0，验证可得条件(H4)满足，计算可得τ2,0≈0.6229.根据定理1，当τ2=0.5时，系统(2)的平衡点是局部渐近稳定的,如图1所示.当τ2=7.78时，系统(2)的平衡点是不稳定的，且出现了混沌吸引子,如图2所示.当τ2=0.63时，计算可得μ2>0,β2<0，由定理1和定理3可得，系统(2)经历了Hopf分支且是上临界和局部渐近稳定的，如图3所示.

取τ2=0.5，计算得g(ω)没有正根.根据定理2，当τ1>0时，系统(2)的平衡点是局部渐近稳定的,如图4和图5所示.

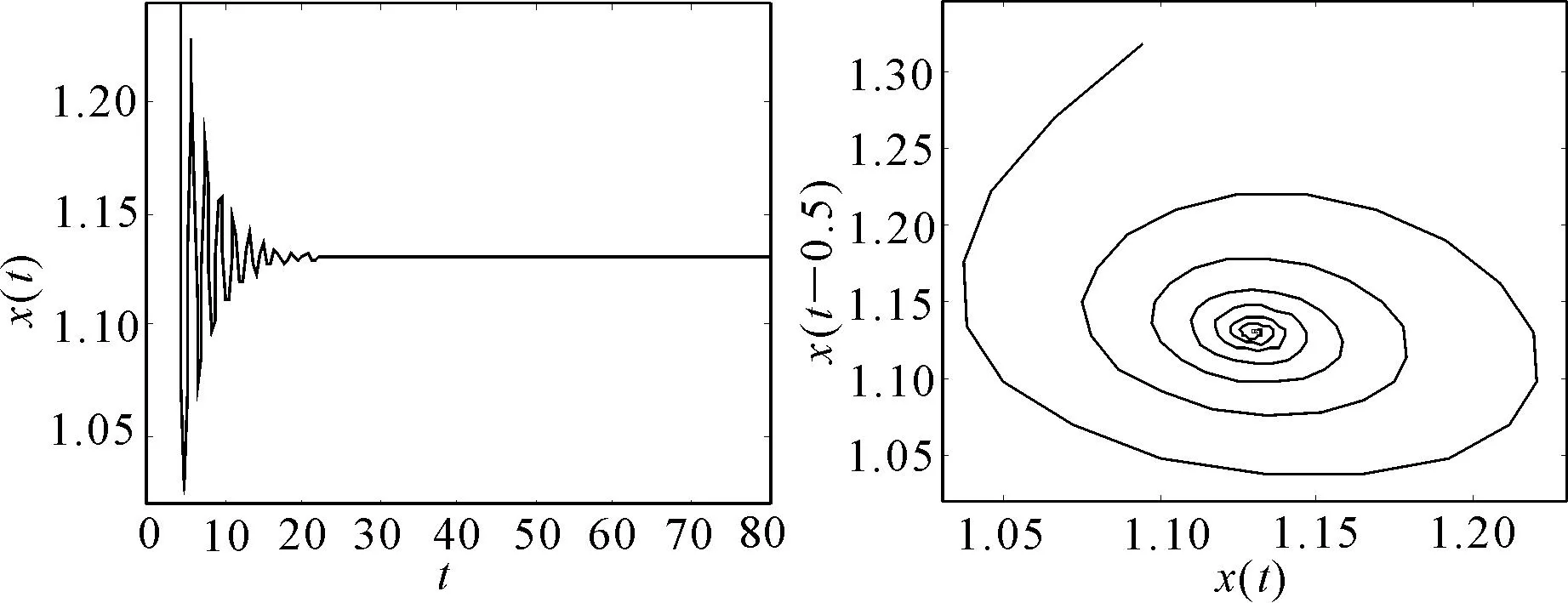
图1　当τ1=0,τ2=0.5时，系统(2)的

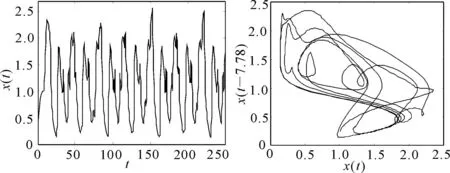
图2　当τ1=0,τ2=7.78时，系统(2)的平衡点不稳定

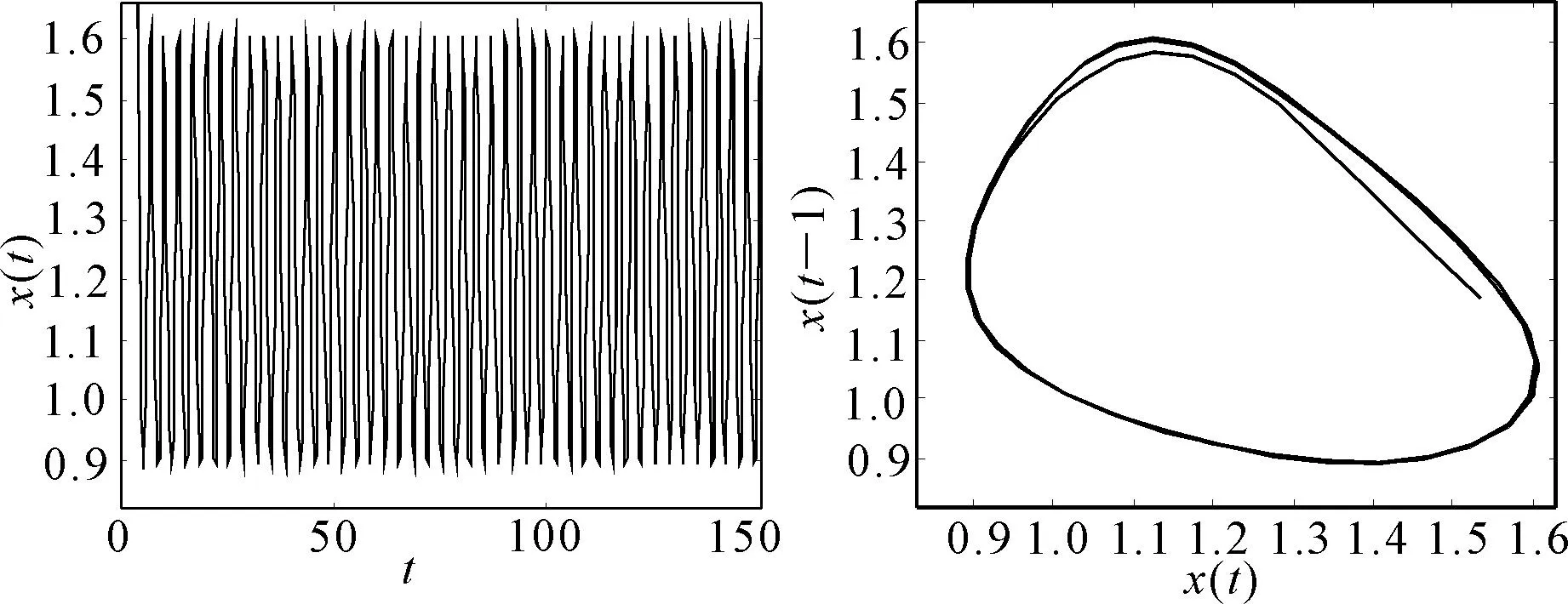
图3　当τ1=0,τ2=0.63时，系统(2)经历了

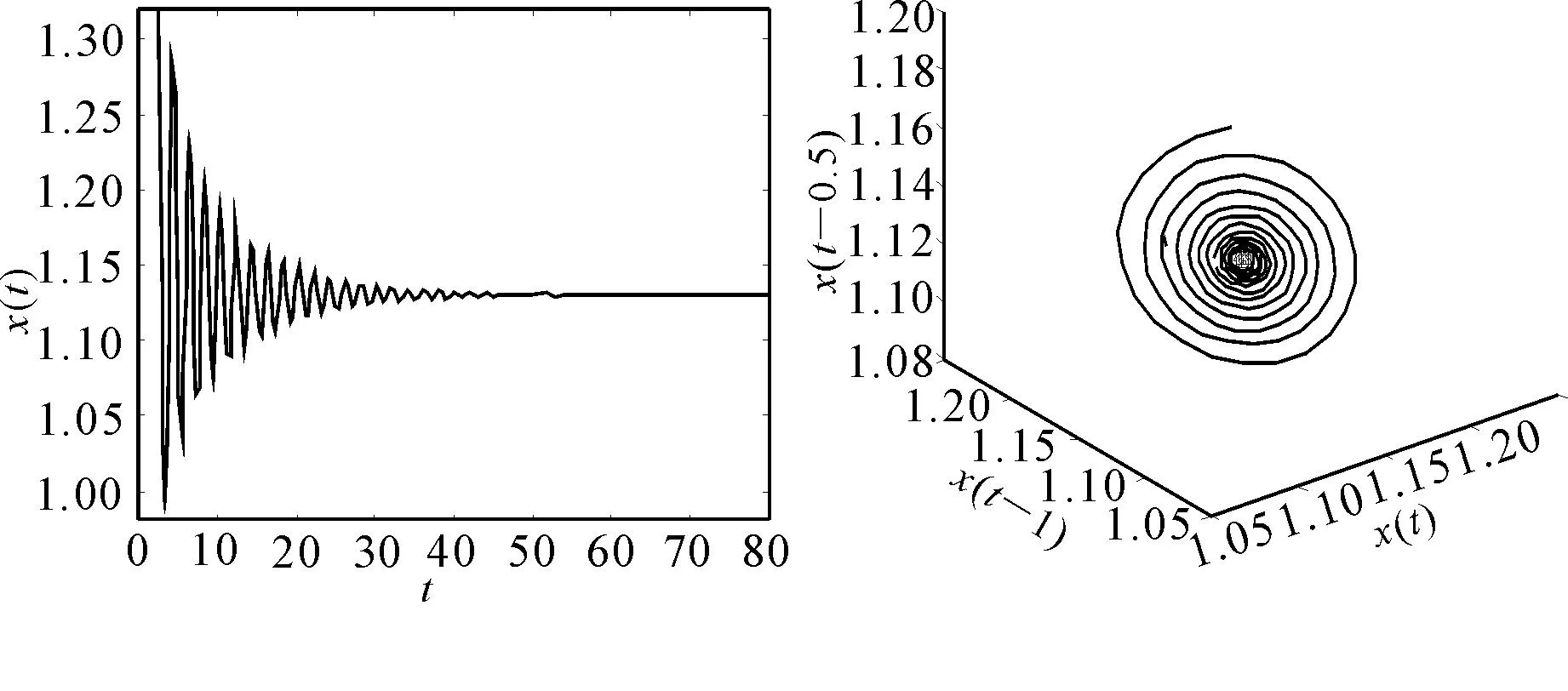
图4　当τ1=1,τ2=0.5时，系统(2)的

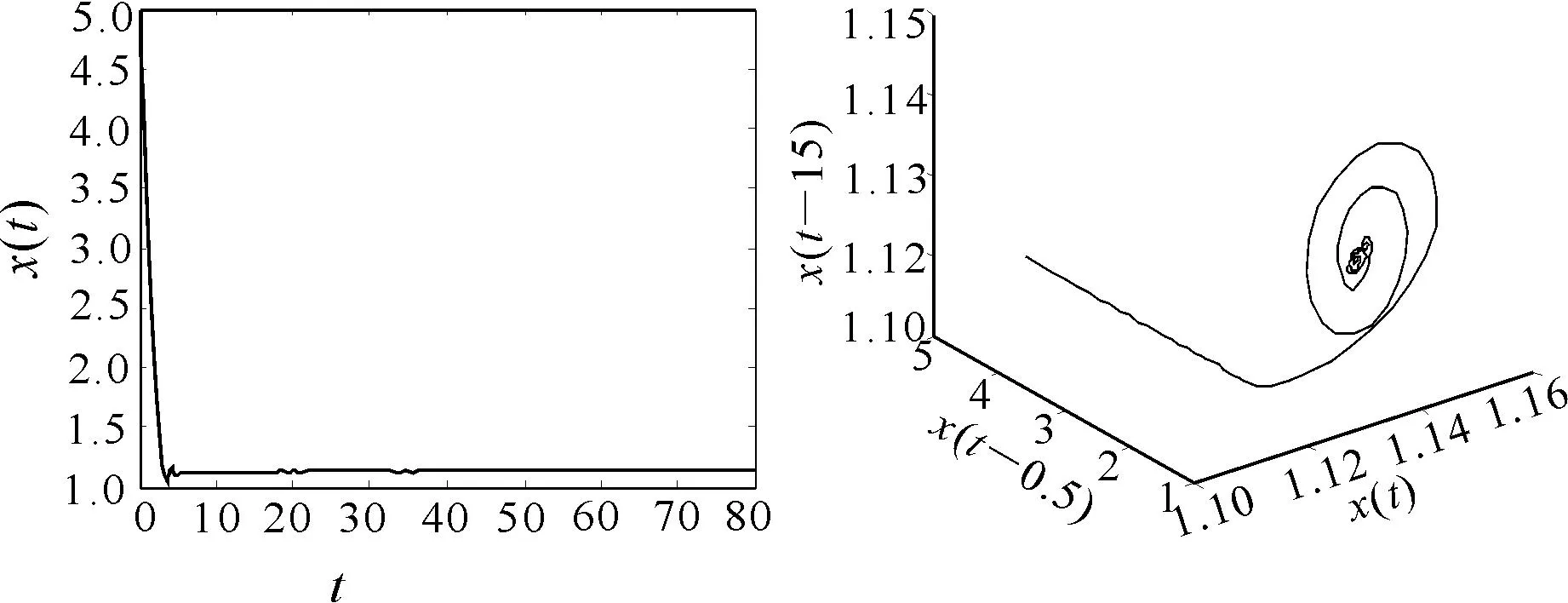
图5　当τ1=15,τ2=0.5时，系统(2)的

4结论

本文研究了双时滞Mackey-Glass系统模型，通过特征值方法对系统的稳定性进行分析.首先，对τ1=0的情形，得到了系统的平衡点稳定的充分条件，并给出了系统的线性稳定性区域和Hopf分支的存在条件．然后，对τ1≠0的情形，讨论了系统平衡点的稳定性和Hopf分支的存在性.然后，应用中心流形定理和规范型方法分析了分支周期解的稳定性和Hopf分支的分支方向.最后，数值模拟验证了理论结果的正确性.利用得到的基本定理，能很好地判断此类模型平衡点的渐近稳定性和周期轨的存在性．

参考文献:

[1]WIGGINSS.Introduction to Applied Nonlinear Dynamical System and Chaos[M].NewYork:Springer,1996:270-278.

[2]WANA,WEIJ.BifurcationanalysisofMackey-Glasselectroniccircuitsmodelwithdelayedfeedback[J].Nonlinear Dyn,2009,57:85-96.

[3]YANGJi-hua,LIUMei.Stabilityandbifurcationanalysisofman-machinesystemwithtimedelay[J].Chin Quart J of Math,2012,27(2):196-203.

[4]侯爱玉，彭震春.离散时滞Mackey-Glass系统的稳定性与分岔[J].湖南工业大学学报，2010,24(5):23-27.

[5]HAIRERE,WANNERG.Solving Ordinary Differential Equations Ⅱ:Stiff and Differential Algebraic Equations[M].NewYork:Springer,1993.

[6]汪芙平，王赞基，郭静波.Mackey-Glass系统的间歇驱动同步实现混沌通信[J].清华大学学报:自然科学版，2003,43(3):33-38.

[7]崔万照，朱长纯，保文星,等.混沌时间序列的支持向量机预测[J].物理学报,2004,53(10):3303-3310.

[8]SHAHVERDIEVEM,NURIEVRA,HASHIMOVRH.ChaossynchronizationbetweentheMackey-Glasssystemswithmultipletimedelays[J].Chaos,Solitons and Fractals,2006,29:854-861.

[9]MACKEYM,HEIDENU.Dynamicdiseasesandbifurcationsinphysiologicalcontrolsystems[J].Funk Biol Med,1982,1:156-164.

[10]BEREZANSKVL,BRAVERMANE,IDELSL.Mackey-Glassmodelofhematopoiesiswithnon-monotonefeedback:stability,oscillationandcontrol[J].Applied Mathematics and Computation,2013,219:6268-6283.

[11]RUANS,WEIJ.Onthezerosoftranscendentalfunctionstostabilityofdelaydifferentialequationswithtwodelays[J].Dyn Contin Discrete Impuls Syst A Math Anal,2003,10:863-874.

[12]HALEJK,LUNELSV.Introduction to Functional Differential Equation[M].NewYork:Springer,1993.

(责任编辑马宇鸿)

作者简介：杨纪华(1983—)，男，河南周口人，讲师，硕士.主要研究方向为微分方程的稳定性与分支理论.

基金项目:国家自然科学基金资助项目(11361046,11301263)；宁夏回族自治区自然科学基金资助项目(NZ13213)；宁夏师范学院创新团队资助项目(zy201207)

收稿日期：2014-06-18;修改稿收到日期:2014-10-10

E-mail:jihua1113@163.com