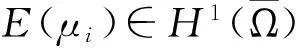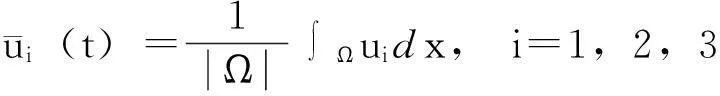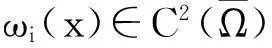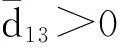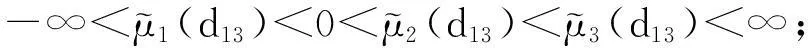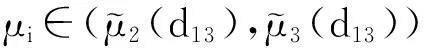含两个消费者和一个生物资源的Armstrong-McGehee扩散系统的稳定性分析

伏升茂，李琦蔚

(西北师范大学数学与统计学院，甘肃兰州　730070)

含两个消费者和一个生物资源的Armstrong-McGehee扩散系统的稳定性分析

伏升茂，李琦蔚

(西北师范大学数学与统计学院，甘肃兰州730070)

摘要：讨论一个含有两个消费者和一个生物资源的Armstrong-McGehee强耦合交错扩散系统.首先，通过线性化方法和构造Lyapunov 函数得到弱耦合反应扩散系统非负平衡点的局部和全局渐近稳定性；其次，分析交错扩散系数对非负平衡点稳定性的影响，证明了当交错扩散系数充分大时会产生Turing不稳定现象.

关键词：Armstrong-McGehee 模型；交错扩散系统；平衡点；稳定性；Turing不稳定

中图分类号：O 175.26

文献标志码：A

文章编号：1001-988Ⅹ(2015)03-0001-06

Stability analysis of an Armstrong-McGehee diffusive system with

two consumers and one biotic resource

FU Sheng-mao,LI Qi-wei

(College of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,Gansu,China)

Abstract:An Armstrong-McGehee strong coupled cross-diffusion system with two consumers and one biotic resource is studied. Firstly，the local and global asymptotical stability of the nonnegative equilibrium points of weakly coupled reaction-diffusion system are obtained by linearization and constructing Lyapunov function.Secondly，the effect of cross-diffusion coefficient on the stability of the nonnegative equilibrium points is discussed.The results show that cross-diffusion can induce Turing instability if the cross-diffusion coefficient is sufficiently large.

Key words:Armstrong-McGehee model;cross-diffusion system;equilibrium point;stability;Turing instability

2013年，Xiao等[1]提出了一类含有两个消费者和一个生物资源的Armstrong-McGehee 模型

(1)

其中，P1,P2和R分别表示两个消费者和生物资源的密度;r和K分别表示生物资源的内禀增长率环境容纳量;Di(i=1,2)是消费者的死亡率;Bi(i=1,2)是消费者的转化率;hi(i=1,2)是消费者的消化系数;Ci(i=1,2)是消费者的捕食率.

作变换t′=tr,u1=P1/kB1,u2=P2/kB2,u3=R/K,并仍记t′为t，再令ai=BiCik/r,bi=kCihi,mi=Di/r(i=1,2),则Armstrong-McGehee模型(1)可化为

(2)

与模型(2)相应的弱耦合反应扩散模型是

其中Ω⊂Rn是边界光滑的有界区域，η为边界∂Ω上的单位外法向量，∂η=∂/∂η,正常数di(i=1,2,3)被称为扩散系数，初值ui0(i=1,2,3)是满足相容性条件的非负不恒为0的光滑函数.

在生态系统中,种群的增长规律往往既依赖于时间和空间变量,还依赖于种群内部之间和不同种群之间的作用关系.因此,我们需要进一步研究交错扩散模型,与模型(3)相应的一个简化的SKT型交错扩散模型是

这里d13,d23为交错扩散系数.

文献[1]主要研究了模型(1)中两个非线性竞争消费者之间的排斥和共存作用，得到了两个消费者潜在的共存区域和已共存的区域，它们共存区域的大小主要随着消费者之间相似性的减少而扩展.经简单计算可知，系统(2)始终有平凡平衡点E0=(0,0,0)和半平凡平衡点E1=(0,0,1)；如果条件

(H1)a1>b1m1+m1

成立，则系统(2)有半平凡平衡点E2=(u*1,0,u*3)，其中

如果条件

(H2)a2>b2m2+m2

在m1(a2-b2m2)=m2(a1-b1m1)和另一些附加条件下，系统(2)才有正平衡点，且正平衡点不是孤立的.

本文主要应用线性化方法和Lyapunov方法讨论扩散系数d1,d2,d3,d13,d23对系统(4)平衡点的稳定性的影响.证明当反应函数的系数满足一定条件时，系统(4)的非负平衡点是全局渐近稳定的，即没有发生扩散导致Turing不稳定现象.但附加一定的条件后，当交错扩散系数充分大时，系统(4)的非负平衡点不稳定，即大交错扩散系数可导致Turing不稳定现象发生.

1弱耦合反应扩散系统的稳定性

本节主要讨论弱耦合反应扩散系统(3)整体解的存在性、一致有界性及其非负平衡点的稳定性.

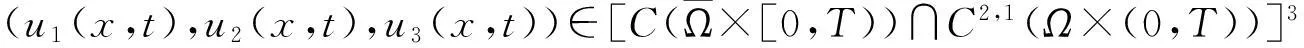
证明由文献[2]可知，系统(3)在[0,T)上存在唯一的古典解，记作U=(u1,u2,u3)，其中T是最大存在区间.由比较原理易知，当(x,t)∈Ω×[0,T)时，ui(x,t)≥0(i=1,2,3).

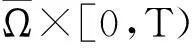
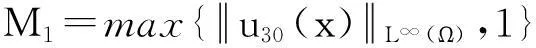
V=u1+u2+u3,k=min{m1,m2},

则由Young不等式有

因此，

下面应用线性化方法分析模型(3)的平衡点的稳定性，其中不稳定性结论是ODE模型(2) 的自然推广，因为(2)的解是(3)的特解.

定理2下列结论成立：

(a)平凡平衡点E0是无条件不稳定的；

(b)当a1m1(1+b1)或a2>m2(1+b2)时，E1不稳定.

(c)当条件(H1)成立，且条件

(H3)a1(b1-1)

成立时，E2是局部一致渐近稳定的;当a1(b1-1)>b1m1(b1+1)或a2m1/[a2+(b2-b1)m1]-m2>0时，E2不稳定.

(d)当条件(H2)成立，且条件

(H5)a2(b2-1)

成立时，E3是局部一致渐近稳定的;当a2(b2-1)>b2m2(b2+1)或a1m2/[a2+(b1-b2)m2]-m1>0时，E3不稳定.

由于(b)，(c)，(d)的证明是类似的，所以我们仅给出(c)的详细证明过程.

设D=diag(d1,d2,d3),L=DΔ+Fu(E2),这里

其中

系统(3)在E2处的线性化系统为ut=Lu.对∀i≥1,Xi是算子L的不变子空间，λ是算子L的特征值当且仅当它是矩阵-μiD+Fu(E2)的特征值.矩阵-μiD+Fu(E2)的特征多项式为

这里

经简单计算，有

其中

当条件(H3),(H4)成立时，a22,a33均为负，即有Ai>0,Ci>0,Hi>0.根据Routh-Hurwits判别法知，φi(λ)=0的三个根λi,1,λi,2,λi,3均有负实部.

设λ=μiξ,则

因为当i→∞时μi→∞，所以

那么当i≥i0时，

故由特征值组成的谱在集合{Reλ≤-δ}中.由文献[3]定理5.1.1知，平衡点E2是局部一致渐近稳定的.】

下面讨论E1,E2,E3的全局渐近稳定性.由文献[4]，有

引理1设a,b为正常数，φ,ψ∈C1[a,∞),φ(t)≥0,ψ(t)有下界，如果ψ′(t)≤-bφ(t),φ′t)≤K,t∈[a,∞),K为正常数，则

定理3(a)当a1

(b)当条件(H1)成立，且条件

成立时，E2是全局渐近稳定的；

(c)当条件(H2)成立,且条件

成立时，E3是全局渐近稳定的.

证明这里我们仅给出(b)的详细证明过程，因为(a)，(b)，(c)的证明是类似的.

设(u1,u2,u3)是系统(3)的唯一解.由定理1和文献[5]定理A2知，对∀t0>0，有

定义Lyapunov函数

其中q=1,p=1+b1u*3，则

由条件(H5),(H6)可知，

由引理1得

(6)

由系统(3)和解的有界性知，当t∈[1,∞)时，g(t)的导数有界.由引理1知，当t→∞时g(t)→∞，因此

利用Pioncare不等式得

(7)

(8)

当t=tn时，由系统(3)的第三式有

(9)

(10)

由(6)式和(10)式得ω1=u*1,ω2=u*2=0,ω3=u*3.所以

这就证明了E2的全局渐近稳定性.

为完善起见，我们给出与E1,E3相应的Lyapunov函数：

2交错扩散对Turing不稳定性的影响

类似于文献[6]定理1.3的证明过程,我们可以得到模型(4)解的整体存在性.本节主要讨论模型(4)中交错扩散系数d13和d23对非负平衡点E2和E3稳定性的影响.

定理4(a)如果条件(H1),(H3),(H4),(H7),(H8)及条件

(b)如果条件(H2),(H5),(H6),(H9),(H10)及条件

证明由于(a)和(b)的证明是类似的，所以我们只对(a)做详细证明.

令K(u)=((d1+d13u3)u1,(d2+d23u3)u2,d3u3)T，则模型(4)在平衡点E2=(u*1,0,u*3)处的线性化问题为

其中

设A(μ)=μKu(E2)-Fu(E2)，记

(11)

其中

考虑如下极限：

由连续性知方程D(d13;μ)=0的三个根满足如下性质：

下面给出满足定理4的条件的两个例子.

例1在模型(4)中令a1=4,b1=3/2,m1=1,a2=3,b2=2,m2=2,d1=d2=d3=1,d13=300(d13较大)，则问题(4)的非负平衡点为(6/25,0,2/5)，这些系数满足定理4(a)的所有条件.

例2在模型(4)中令a1=4,b1=4,m1=4,a2=8,b2=5/4,m2=2,d1=d2=d3=1,d23=200(d23较大),则问题(4)的非负平衡点为(0,14/121,4/11)，这些系数满足定理4(b)的所有条件.

3结论

本文主要研究了含两个消费者和一个生物资源的Armstrong-McGehee交错扩散系统的稳定性.由定理2和定理3知,当模型(3)的系数满足条件(H1)～(H10)时,弱耦合反应扩散模型(3)与ODE模型(2)的解的稳定性相似,也就是自扩散并没有改变系统的稳定性.但是,由定理4可知,当附加条件(H11)和(H12)后,若交错扩散系数充分大,就会有扩散导致 Turing不稳定现象发生.

参考文献:

[1]XIAO X,FUSSMANN G F.Armstrong-McGehee mechanism revisited:Competitive exclusion and coexistence of nonlinear consumers[J].JTheoreticalBiology,2013,339:26-35.

[2]LADYZENSKAJA O A,SOLONNIKOV V A,URAL′CEVA N N.LinearandQuasilinearEquationsofParabolicType[M].Providence,RI:American Mathematical Society,1968.

[3]HENRY D.GeometricTheoryofSemilinearParabolicEquations[M].Lecture Notes in Mathematics Vol.840.Berlin:Springer,1993.

[4]王明新.非线性椭圆型方程[M].北京:科学出版社,2010.

[5]BROWN K J,DUNE P C,GARDNER R A.A similinear parabolic system arising in the theory of superconductivity[J].JDifferentialEquations,1981,40(2):232-252.

[6]FU S M,ZHANG L N,HU P.Global behavior of solutions in a Lotka-Volterra predator-prey model with prey-stage structure[J].NonlinearAnal:RWA,2013,14(5):2027-2045.

(责任编辑马宇鸿)

作者简介：伏升茂(1966—)，男，甘肃秦安人，教授，博士研究生导师.主要研究方向为偏微分方程.

基金项目:国家自然科学基金资助项目(11061031)

收稿日期：2014-09-12;修改稿收到日期:2014-10-27

E-mail:fusm@nwnu.edu.cn;liqiwei369@163.com