辊弯成型有限元模拟中接触问题处理的探讨

赵生莲

摘 要： 冷弯生产技术是金属板带深加工的重要领域。本文对辊弯成型有限元模拟中接触问题的处理进行了探讨。

关键词： 冷弯成型 接触 有限元

接触问题是一个非常复杂的边界非线性问题，在冷弯成型的过程中，接触状态在不断发展和变化，使得接触的判断事先难以确定。辊弯成型时板材与轧辊之间处于不断接触、分离、再接触这样的不断变化之中，因此分析时需要准确跟踪接触前各个物体的运动和接触发生后这些物体之间的相互作用，正确表述接触面之间的摩擦行为。产生接触的两个物体必须满足无穿透约束条件。

1.接触问题的无穿透约束

在数学上施加无穿透接触约束的方法有拉格朗日乘子法、罚函数法和直接约束法。

1.1拉格朗日乘子法（the Lagrange multiplicator method）

拉格朗日乘子法是通过拉格朗日乘子施加接触体必须满足的非穿透约束条件的带约束极值问题的描述方法。这种方法是把约束条件加在一个系统中最完美的数学描述。该方法增加了系统变量数目，并使系统矩阵主对角线元素为零。这就需要在数值方案的实施中处理非正定系统，数学上将发生困难，需实施额外的操作才能保证计算精度，从而使计算费用增加。另外，由于拉格朗日乘子与质量无关，导致这种由拉格朗日乘子描述的接触算法不能用于显示动力撞击问题分析。

拉格朗日乘子技术经常用于采用特殊的界面单元描述接触的接触问题分析。该方法限制了接触物体之间的相对运动量，并且需要预先知道接触发生的确切部位，以便施加界面单元。这样的额外要求对于撞击、压力加工等通常事先并不知道准确接触区域所在的一类问题是难于满足的。

1.2罚函数法

罚函数法是一种施加约束的数值方法。其原理是一旦接触区域发生穿透，罚函数便夸大这种误差的影响，从而使系统的求解（满足力的平衡和位移协调）无法正常进行。换言之，只有在约束条件满足之后，才能求解出有实际物理意义的结果。

用罚函数法施加接触约束的方法可以类比成在物体之间加非线性弹簧所起的作用。该方法不增加未知量数目，但增加系统矩阵带宽。其优点是数值上实施比较容易，在显示动力分析中被广泛应用。不足是罚函数选择的不当将对系统的数值稳定性造成不良影响。

1.3直接约束法

用直接约束法处理接触问题是追踪物体的运动轨迹，一旦探测出发生接触，便將接触所需的运动约束（即：法向无相对运动，切向可滑动）和节点力（法向压力和切向摩擦力）作为边界条件直接施加在产生接触的节点上，直接约束法对接触的描述精度高，具有普遍适用性，不需要增加特殊的界面单元，也不涉及复杂的接触条件。该方法不增加系统的自由度数，但由于接触关系的变化会增加系统矩阵的带宽。在处理压力加工时采用直接约束法，基于直接约束法的接触算法是解决接触物体的通用算法，特别是对于大面积接触和事先无法预知接触发生区域的接触问题，程序能根据物体的运动约束和相互作用自动探测接触区域，施加接触约束。进行接触计算时先进行接触探测，所谓接触探测是在每个增量步开始时，检查每个可能接触的结点的空间位置，看它是否位于某一接触段附近，并且离该接触段的距离足够近。从理论上讲，结点恰好落在某个接触段时认为发生接触，但数值计算过程中，要精确描述恰好位于某一个接触段上比较困难，这要靠接触容限解决。当某结点落在接触容限内就被认为与接触段相接触了，对于实体单元，接触容限δ可取单元最小尺寸的1/20；对于用于板料成形有限元分析的壳体单元，δ可取最小厚度的1/2。数值计算表明，接触距离容限的大小对接触求解精度和计算效率影响很大。接触距离容限越小，计算结果的精度就越高。但是，如果接触距离容限太小，就难以探测出结点与接触片相接触，而且一旦步长稍大就会在多点产生穿透，需很细的时间分布，这样在提高精度的同时增加了计算费用。这时就要靠偏斜系数B（0≤B≤1）解决，使接触距离的误差范围发生偏移，以便在接触体外表面的接触距离误差比内表面的接触距离误差稍大。

以上所述是针对实体单元，因为实体单元不仅存在体积闭锁问题，而且对于薄板成型不如板壳单元计算效率高。壳体单元是一种结构单元，它与实体单元不同之处在于它的几何描述是用中面的有限元网格和中面结点所在的壳体厚度表示。壳体的接触探测与实体单元有所不同，壳体上的结点发生接触是当壳体结点的空间位置加上或减去其厚度一半后正好落入另一个接触片的接触距离误差区域时，就发生壳体与该接触片接触。

2.刚体与变形体之间的接触约束

变形体与刚体接触的无穿透约束是通过把接触节点自由度转换到刚性接触段/片的局部坐标系后，给定法向位移边界条件实现的，用方程描述为：

代表产生接触的节点在接触段/片上的局部坐标转换，b代表无接触的其他节点，当然也无坐标系转换，对这些局部坐标系转换的节点，局部法向位移约束应等于刚体沿接触节点所在的刚体法线方向的位移增量。

3.接触摩擦分析

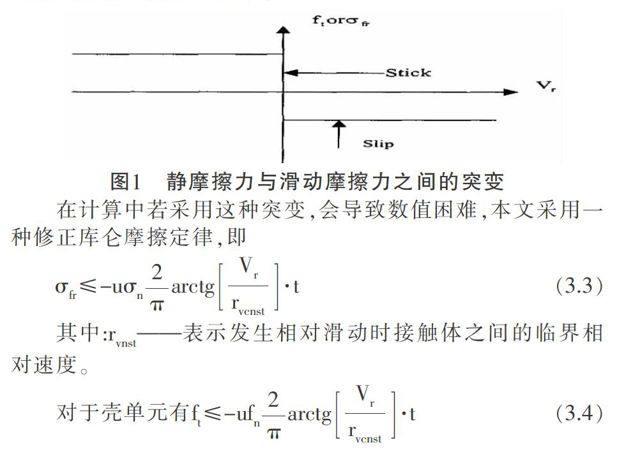
图1 静摩擦力与滑动摩擦力之间的突变

在计算中若采用这种突变，会导致数值困难，本文采用一种修正库仑摩擦定律，即

σ■≤-uσ■■arctg■·t（3.3）

其中：r■——表示发生相对滑动时接触体之间的临界相对速度。

对于壳单元有f■≤-uf■■arctg■·t（3.4）

对于采用的摩擦模型，问题的关键就在于摩擦系数的正确选取。如果摩擦系数选取不正确，则对计算结果的精度影响非常大。

4.结语

本文对辊弯成型接触问题的处理进行了探讨，对辊弯成型有限元模拟有一定的实用价值。

参考文献：

[1]石京，王先进.国内外冷弯成形研究最新进展.轧钢.1998，10（5）.

[2]周瑛.辊式成型过程的弹塑性大变形样条有限元模拟.东北重型机械学院博士学位论文，1996.

[3]徐树成.辊弯成形的三维大变形有限元模拟.秦皇岛：燕山大学学位论文，1997，12.

[4]韩志武，刘才.冷弯成型数值模拟与孔型CAD集成.钢铁，2001，36（7）.