理解对应:从“标准图形”到“变式图形”
蔡美娟
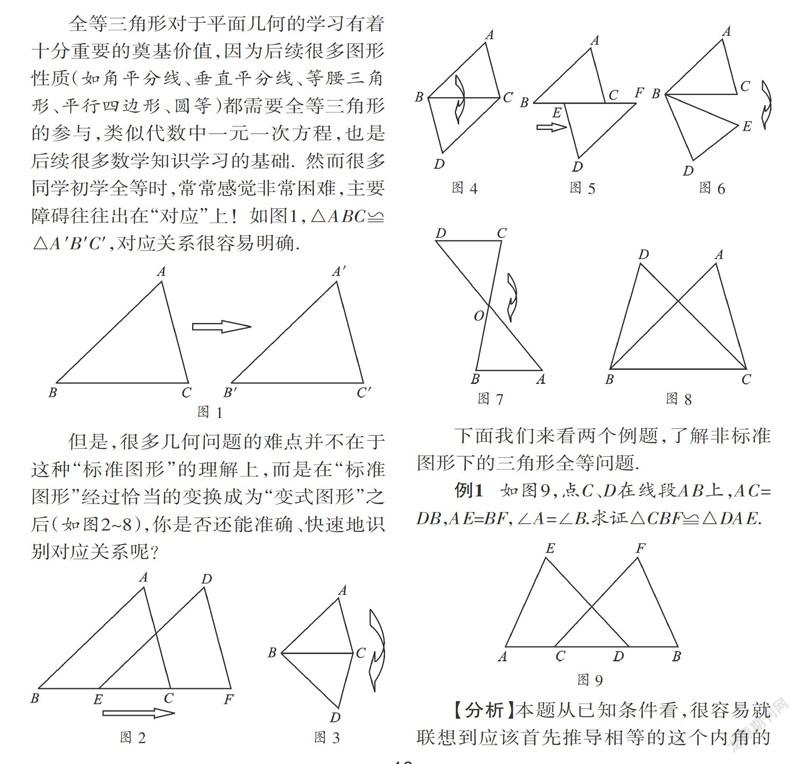

全等三角形对于平面几何的学习有着十分重要的奠基价值,因为后续很多图形性质(如角平分线、垂直平分线、等腰三角形、平行四边形、圆等)都需要全等三角形的参与,类似代数中一元一次方程,也是后续很多数学知识学习的基础.然而很多同学初学全等时,常常感觉非常困难,主要障碍往往出在“对应”上!如图1,△ABC≌△A′B′C′,对应关系很容易明确.
但是,很多几何问题的难点并不在于这种“标准图形”的理解上,而是在“标准图形”经过恰当的变换成为“变式图形”之后(如图2~8),你是否还能准确、快速地识别对应关系呢?
下面我们来看两个例题,了解非标准图形下的三角形全等问题.
例1 如图9,点C、D在线段AB上,AC=DB,AE=BF,∠A=∠B.求证△CBF≌△DAE.
【分析】本题从已知条件看,很容易就联想到应该首先推导相等的这个内角的另一条边也是对应相等的,也就是AD=BC,然后再证明三角形全等.
证明:因为AC=DB(已知),
所以AC+CD=BD+CD,即AD=BC.
在△CBF和△DAE中,
AE=BF,
∠A=∠B,
AD=BC.
∴△CBF≌△DAE(SAS).
例2 如图10所示,AD∥BC,AD=CB,求证:△ADC≌△CBA.
【分析】本题是在两个三角形有公共边AC的情况下进行考虑的,也就是有两组边对应相等.若要根据SAS来判断两个三角形全等,应该首先推导以AC和AD的夹角∠2与CA和CB的夹角∠1也是对应相等的,然后再证明三角形全等.
证明:因为AD∥BC,
所以∠1=∠2.
在△ADC和△CBA中,
AD=CB,
∠1=∠2,
AC=CA.
所以△ADC≌△CBA(SAS).
【解后反思】如果再由证得的全等三角形出发,同学们还能得出该四边形ABCD中对边AB、CD有怎样的数量关系、位置关系吗?
(作者单位:江苏省海安县李堡镇初级中学)

