必修三、选修23单元测试

一、填空题（本大题共14小题，每小题5分，共70分）

1.若Cn18-C2n+918=0（n∈N*），则n=    .

2.（2x-1x）6的二项展开式中的常数项为    .

3.甲、乙两种水稻试验品种连续4年的单位面积平均产量如下：

品种第1年第2年第3年第4年

甲9.89.910.210.1

乙9.7101010.3

其中产量比较稳定的水稻品种是    .

4.从5名男生和5名女生中任选3人参加综合实践活动，则所选同学中既有男生又有女生的概率是    .

5.如图，随机向半径为R的⊙O内丢一粒豆子，则豆子落入该圆的内接正△ABC内的概率是    .

6.下面是某小组学生在一次数学测验中的得分茎叶图，则该组男生的平均得分与女生的平均得分之差是    .

7.执行右边的程序框图，若p=15，则输出的n=    .

8.根据如图所示的伪代码，可知输出的结果a为    .

9.某校100位学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60）、[60，70）、[70，80）、[80，90）、[90，100].则图中a的值为    .

10.在5次独立重复试验中，随机事件A恰好发生1次的概率不大于其恰好发生2次的概率，则事件A在一次试验中发生的概率P的最小值是    .

11.随机变量ξ的分布列如下：

ξ-101

Pabc

其中a，b，c成等差数列，若期望E（ξ）=13，则方差V（ξ）的值是    .

12.若（2x+1）7=a0+a1（x+1）+a2（x+1）2+…+a7（x+1）7，则a4=    .

13.将标号为1，2，3，4，5，6的6张卡片放入3个不同的信封中，若每个信封放2张，其中标号为1，2的卡片放入同一信封，则不同的放入方法共有  种.

14.有两个细胞，每个细胞每次分裂成2个细胞或死亡的概率均为12，则分裂两次后有细胞存活的概率为    .

二、解答题（本大题共6小题，共90分）

15.（本题满分16分）

某车间甲组有10名工人，其中有4名女工人;乙组有10名工人，其中有6名女工人.现采用分层抽样（层内采用不放回简单随即抽样）从甲、乙两组中共抽取4名工人进行技术考核.

（1）求从甲、乙两组各抽取的人数;

（2）求从甲组抽取的工人中恰有1名女工人的概率;

（3）求抽取的4名工人中恰有2名男工人的概率.

16.（本小题满分14分）

已知（x+12x）n展开式中前三项系数依次为等差数列.

（1）求n的值;

（2）求展开式中系数最大项.

17.（本题满分16分）

男运动员6名，女运动员4名，其中男女队长各1人，从中选5人外出比赛.

（1）若选出男运动员3名，女运动员2名，有多少种不同的选派方法？

（2）若队长至少有1人参加，有多少种不同的选派方法？

（3）若至少有1名女运动员，有多少种不同的选派方法？

（4）若既要有队长，又要有女运动员，有多少种不同的选派方法？

18.（本题满分16分）

设有关于x的一元二次方程x2+2ax+b2=0.

（1）若a是从0，1，2，3四个数中任取的一个数，b是从0，1，2三个数中任取的一个数，求上述方程有实根的概率.

（2）若a是从区间[0，3]任取的一个数，b是从区间[0，2]任取的一个数，求上述方程有实根的概率.

19.（本小题满分16分）

某高中为了推进新课程改革，满足不同层次学生的需求，决定从高一年级开始，在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座.（规定：各科达到预先设定的人数时称为满座，否则称为不满座）

统计数据表明，各学科讲座各天的满座概率如下表：

信息技术生物化学物理数学

周一1414141412

周三1212121223

周五1313131323

（1）求数学辅导讲座在周一、周三、周五都不满座的概率;

（2）设周三各辅导讲座满座的科目数为ξ，求随机变量ξ的分布列和数学期望.

20.（本题满分16分）

已知（1+x4）2n=a0+a1x+a2x2+…+a2nx2n（n∈N*）.

（1）若a0+a1+a2+…+a2n=625256，求a3的值;

（2）若存在整数k（0≤k≤2n），对任意的整数m（0≤m≤2n），总有ak≥am成立，这样的k是否唯一？并说明理由.

参考答案

一、填空题

1. 3

2. 60

3. 甲

4. 56

5. 334π

6. 2

7. 5

8. 3

9. a=0.005

10. 13

11. 59

12. -560

13. 18

14. 3964

二、解答题

15.解：（1）由于甲、乙两组各有10名工人，根据分层抽样原理，要从甲、乙两组中共抽取4名工人进行技术考核，则从每组各抽取2名工人.

（2）记A表示事件：从甲组抽取的工人中恰有1名女工人，则

P（A）=C14C16C210=815.

（3）Ai表示事件：从甲组抽取的2名工人中恰有i名男工人，i=0，1，2

Bj表示事件：从乙组抽取的2名工人中恰有j名男工人，j=0，1，2

B表示事件：抽取的4名工人中恰有2名男工人.

Ai与Bj独立，i，j=0，1，2，且B=A0·B2+A1·B1+A2·B0

故P（B）=P（A0·B2+A1·B1+A2·B0）

=P（A0）·P（B2）+P（A1）·P（B1）+P（A2）·P（B0）

=C24C210·C24C210+C14C16C210·C16C14C210+C26C210·C26C210=3175

所以抽取的4名工人中恰有2名男工人的概率为3175.

16.解：（1）由题意，前三项系数分别为C0n，12C1n，14C2n，

则C1n=C0n+14C2n，解得n=1（舍），n=8.

（2）设第r+1项系数为tr+1，且设第r+1项系数最大，则

tr+1≥tr

tr+1≥tr+2即Cr8（12）r≥Cr-18（12）r-1

Cr8（12）r≥Cr+18（12）r+1，解得2≤r≤3，且t3=t4=7，

所以展开式中最大项为第三、第四项.

17.解：（1）C36C24=120（种）;

（2）C12C48+C22C38=140+56=196（种）;

（3）C510-C56=246（种）;

（4）C510-C58-C45=191（种）;

答：略

18.解：设事件A为“方程a2+2ax+b2=0有实根”.

当a>0，b>0时，方程x2+2ax+b2=0有实根的充要条件为：a≥b.

（1）基本事件共12个：（0，0），（0，1），（0，2），（1，0），（1，1），（1，2），（2，0），（2，1），（2，2），（3，0），（3，1），（3，2）.

其中第一个数表示a的取值，第二个数表示b的取值.

事件A中包含9个基本事件，事件A发生的概率为P（A）=912=34.

（2）试验的全部结果所构成的区域为{（a，b）|0≤a≤3，0≤b≤2}.

构成事件A的区域为{（a，b）|0≤a≤3，0≤b≤2，a≥b}.

所以所求的概率为=3×2-12×223×2=23.

19.解：（1）设数学辅导讲座在周一、周三、周五都不满座为事件A，则

P（A）=（1-12）（1-23）（1-23）=118.

（2）ξ可能取值为0，1，2，3，4，5，

P（ξ=0）=（1-12）4（1-23）=148，

P（ξ=1）=C1412（1-12）3（1-23）+（1-12）423=18，

P（ξ=2）=C24（12）2（1-12）2（1-23）+C1412（1-12）323=724，

P（ξ=3）=C34（12）3（1-12）（1-23）+C24（12）2（1-12）223=13，

P（ξ=4）=（12）4（1-23）+C34（12）3（1-12）23=316，

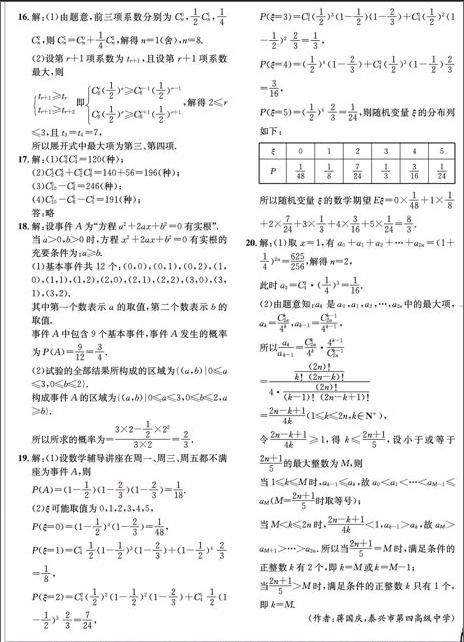
P（ξ=5）=（12）423=124，则随机变量ξ的分布列如下：

ξ012345

P1481872413316124

所以随机变量ξ的数学期望Eξ=0×148+1×18+2×724+3×13+4×316+5×124=83.

20.解：（1）取x=1，有a0+a1+a2+…+a2n=（1+14）2n=625256，解得n=2，

此时a3=C34·（14）3=116.

（2）由题意知：ak是a0，a1，a2，…，a2n中的最大项，ak=Ck2n4k，ak-1=Ck-12n4k-1，

所以akak-1=Ck2n4k·4k-1Ck-12n

=（2n）！k！（2n-k）！4·（2n）！（k-1）！（2n-k+1）！

=2n-k+14k（1≤k≤2n，k∈N*），

令2n-k+14k≥1，得k≤2n+15，设小于或等于2n+15的最大整数为M，则

当1≤k≤M时，ak-1≤ak，故a0<a1<…<aM-1≤aM（M=2n+15时取等号）;

当M<k≤2n时，2n-k+14k<1，ak-1>ak，故aM>aM+1>…>a2n.所以当2n+15=M时，满足条件的正整数k有2个，即k=M或k=M-1;

当2n+15>M时，满足条件的正整数k只有1个，即k=M.

（作者：蒋国庆，泰兴市第四高级中学）