滇西秃杉人工林林分直径结构分析

雷阳+许彦红+段成波+李骄+梁丽+熊宗豪

摘要：通过对62块典型样地进行调查，采用相对直径株数累积百分数、正态分布函数、Weibull分布函数、Logistic生长函数等对不同密度和不同年龄的秃杉人工林分进行了直径结构分析和函数拟合，并进行了统计检验。研究结果表明：随林分密度减小，直径株数累积百分数曲线规律性右移;在任意的相同株数累积百分数所对应的不同密度的直径，密度越大，直径越小;Logistic生长函数对于腾冲秃杉人工林直径分布的拟合效果优于Weibull分布函数和正态分布函数，可用于该研究区秃杉人工林林分直径分布及生长量预测。

关键词：秃杉;人工林;直径结构;函数拟合

中图分类号：S718.5

文献标识码：A文章编号：16749944（2014）12006104

1引言

林分直径结构在许多树种林分中都具有其特定的分布状态以及结构规律性，可以在定向培育目标树种的过程中及时调整林分的结构，让目标树种能更好地生长。在林分内各种大小直径林木按径阶的分配状态，称作林分直径结构（Stand diameter structure），亦称林分直径分布（Stand diameter distribution）[1]。

秃杉[2，3] （Taizemnia flousiana Gaussen）除了对生长环境湿度要求较高外，对其他要求并不严格，这造就其具有广泛的适应性，可作为我国常用造林更新树种。云南省是我国秃杉天然林和人工林主要分布区之一，因此，秃杉直径结构的研究对于秃杉大径材培育技术研究和云南省速生丰产乡土树种产业经济的发展都具有重要的意义。

2研究区概况

选取云南西部腾冲县作为研究区域，是秃杉天然林和人工林分布最为集中地区，生长最具代表性。研究区属亚热带季风气候类型，多年平均气温14.9℃。平均降雨量1425.4mm，1月为最冷月均温7.5℃，8月均温19.7℃，年日照指数2176h，日照百分率49%，年均相对湿度78%。其地带性土壤有灌丛草甸土、暗棕壤、棕壤、黄棕壤、黄壤和红壤，非地带性土壤有棕色石灰土、黑色石灰土和火山石灰土。

3研究内容及方法

3.1资料收集

按林分不同龄级及立地条件选设标准地，面积不小于400m2，闭合差小于1/200。对标准地内的树木进行每木检尺[4～7]，起测径阶按所选标准地的林分生长情况确定，尽量包括最小径阶;调查林木胸径、林分郁闭度、年龄等基本因子，记载标准地的地理位置、海拔、坡向、坡度、坡位、土壤类型和土层厚度等立地环境因子，以及林下灌木、草本的种类、盖度、平均高度和分布等;对林分经营情况如修枝抚育、间伐等经营措施进行调查记录。共设置调查标准地62块，主要分布于海拔1740～2386m，林分郁闭度0.60～0.95，林分年龄6～58年。

3.2数据整理

用Excel软件和SPASS软件对外业调查数据进行处理，统计每块样地各径阶株数分布情况，并求算林分平均胸径Dg和算术平均胸径：

Dg=1Nki=1nidi2（1）

=1NNi=1di（2）

式中：N为林分内林木总株数;di为第i株林木的断面积和胸径。

3.3研究方法

采用相对直径株数百分数累计法、概率分布函数法和生长函数法分别对腾冲县秃杉人工林的直径结构进行分析和拟合，其中概率分布函数法采用正态分布[8]和Weibull分布[9～11]，函数，生长函数法采用著名的Logistic生长函数[12～15]，拟合结果用卡方检验判定各函数拟合效果。

3.3.1正态分布函数

标准正态分布的概率密度函数为：

f（x）=12πσe-（x-）22σ2（3）

式中：为随机变量x的数学期望;σ为随机变量x的标准差。

3.3.2三参数Weibull分布密度函数

f（x）=0

cb（x-ab）c-1·exp-（x-ab）cx≤a

x>a，b>0，c<0

（4）

式中：a被定义为位置参数，a的取值为林分中最小径阶的林木的直径下限值;b为尺度参数;c为形状参数。

在用Weibull分布密度函数拟合林分直径分布时，参数a为直径最小径阶的下限值，而对于参数b和参数c，通常用最大似然估计法求解。

3.3.3Logistic生长函数

应用于林分直径分布模型时，形式为：

y=c1+ep-qx（5）

式中：y为各径阶对应的累积频率;x为径阶中值。c，p，q>0，c为f（x）的上渐进值;p为与f（x）初值有关的参数;q为内秉生长率。

4结果与分析

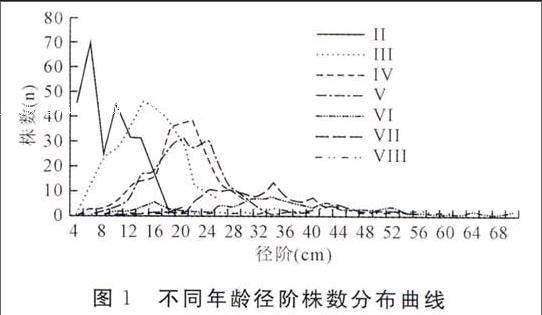
4.1不同年龄段各径阶株数分布

将调查样地秃杉按龄级（即Ⅰ龄级：0～5年，Ⅱ龄级：6～10年，Ⅲ龄级：11～15年，Ⅳ龄级：16～20年，Ⅴ龄级：21～25年，Ⅵ龄级：26～30年，Ⅶ龄级：31～35年，Ⅷ龄级：36～40年，Ⅸ龄级：41年以上）统计各径阶株数，得出各径阶株数分布曲线如图1所示。可看出各龄级林分直径结构表现为以某一径阶为峰点的单峰山状曲线，并且随着林分年龄的增长，顶点规律性右移，峰点对应的直径可看作是林分算术平均胸径;林分直径分布曲线随着林分年龄的增长由尖峭慢慢变为平坦，林分径阶离散度由小变大，分布曲线由左偏慢慢向右偏过渡。同时可以看出，Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ龄级曲线之间峰点相对右移程度较大，说明秃杉在Ⅱ到Ⅵ龄级生长速度快;到Ⅶ、Ⅷ龄级时，曲线峰点右移不明显，说明秃杉生长进入缓慢期。

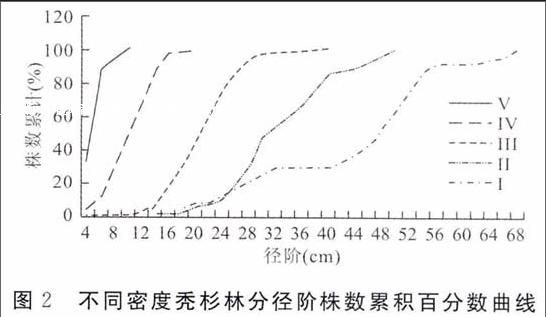
4.2不同密度林分的株数累积直径分布endprint

将林分密度分为5级，即Ⅰ级：500株/hm2以下，

图1不同年龄径阶株数分布曲线

Ⅱ级：501～1000，Ⅲ级：1001～1500，Ⅳ级：1501～2000，Ⅴ级：2001以上。按林分密度不同对腾冲县秃杉人工林林分做径阶株数累积曲线，如图2所示，随林分密度减小，株数累积曲线规律性右移;在任意的相同累积百分数所对应的不同密度的直径，密度越大，直径越小。在同一径阶上林分密度越大，其株数积累率越高，说明直径分布曲线随着林分密度的减少而提前右偏;在任意的相同株数累积百分数时，高密度林分的株数累积百分数所对应的直径均小于低密度的林分，亦即在获取目标材种的时候，同样的株数累积百分数，密度越高的林分所对应的平均直径越小，整个林分的直径分布较窄，材种规格低。

图2不同密度秃杉林分径阶株数累积百分数曲线

4.3正态分布、Weibull分布函数、Logistic生长函数

拟合

4.3.1参数估计

筛选出调查样地林木株数满足进行直径分布函数拟合条件的13块具有代表性的样地，年龄从6～32年排序，分别用正态分布函数、Weibul1分布函数和Logistic生长方程进行拟合，拟合方程参数如表1所示。

4.3.2分布拟合及x2检验

由表1中每块样地的参数估计值，分别求出正态分布、Weibull分布函数和Logistic生长函数各径阶对应的理论株数，计算结果与实测株数进行卡方检验，在=0.05时，查出对应的卡方值，函数拟合检验结果如表2所示。

由表2看出，在α=0.05时，正态分布函数可以较好拟合23、24、25、21、32、8和38号样地的秃杉直径分布;Weibull函数可以较好拟合25、31、32、48和38号样地的秃杉直径结构分布;Logistic函数可以较好拟合14、23、25、21、27、31、32、17、8、48和43号样地的林分直径结构分布。其中23、24、25、21和8号样地为未经过间伐的样地，其他样地均经历过不同程度的抚育间伐活动。13块样地年龄由小到大，14号样地林分年龄6年，43号样地林分年龄32年。从样地林分年龄来看，三参数Weibull函数和Logistic函数可以拟合秃杉各年龄阶段间伐与未间伐的林分样地的直径分布，但Logistic函数可以拟合的范围更大，其拟合效果和适用性优于Weibull函数;正态分布适宜拟合中幼龄未经过间伐活动的林分样地的林分直径分布。

5结论与讨论

（1）秃杉人工林林分直径株数分布曲线呈现出以某一径阶为峰点的单峰山状曲线，随着林分年龄的增大，林分直径株数分布曲线由左偏逐渐转为右偏。

（2）随林分密度减小，直径株数累积百分数曲线规律性右移;在任意的相同累积百分数所对应的不同密度的直径，密度越大，直径越小。

（3）正态分布、Weibull分布函数和Logistic生长函数对于秃杉直径结构规律的模拟均具有一定的适用性。本文在对腾冲县秃杉人工林调查样地的直径结构分析时，发现正态分布较适宜未经抚育间伐的林分，而Weibull分布函数和Logistic生长函数的适应性较广，且适用性Logistic生长函数>Weibull分布函数。至于Logistic生长函数以外的其他生长方程能否用于腾冲县秃杉人工林直径结构拟合还有待于更多的研究。

（4）通过对秃杉人工林直径结构的分析，发现未经抚育间伐或者抚育间伐措施不及时等的样地其林分内林木直径分化严重，不利于大径材秃杉人工林的培育。为了缩短大径材林木培育的时间，建议根据不同立地条件下秃杉人工林生长状况的优劣，积极探索秃杉速生期内较适宜的间伐强度和间隔期，缩短大径材培育期限，以期在一定的轮伐期内获取更多的秃杉大径材林木。

参考文献：

[1]盂宪宇.测树学[M].2版.北京：中国林业出版社，1996.

[2]陶国祥.秃杉[M].昆明：云南科技出版社，2001.

[3]杨宁，陈璟，杨满元，等. 贵州雷公山秃杉林不同林冠环境下箭竹分株种群结构特征[J].西北植物学报，2013，33（11）：2326～2331.

[4]李兰花.北京市低山区残次水土保持林评价[D].北京：北京林业大学，2011.

[5]马克平，黄建辉，于顺利，等.北京东灵山地区植物群落多样性的研究：Ⅱ富度、均匀度和物种多样性指数[J]. 生态学报，1995（3）：268～277.

[6]刘建新，曲晓晶，侯淑艳，等. 北京市低山区低效油松人工林林分结构研究[J].安徽农业科学，2013，41（16）：7204～7206.

[7]曾祥谓，玉 宝，乌吉斯古楞，等. 云冷杉过伐林主要树种结构特征分析[J].林业科学研究，2014，27（4）：481～486.

[8]韩东锋，钱拴提，孙丙寅，等.油松飞播林直径结构规律研究[J].西北林学院学报，2008，23（5）：182～187.

[9]Bailer R L;Dell T R Quantifying diameter distributions with the Weibull function [J].For Sci，1973，19（2）：97～104.

[10]许彦红，杨宇明，杜凡.西双版纳热带雨林林分直径结构研究[J].西南林学院学报，2004，24（2）：16～18.

[11]姜磊，陆元昌，廖声熙.滇中高原云南松林分直径结构研究[J].林业科学研究，2008，21（1）：126～130.

[12]崔丽红，兰永生，王丽华，等. 河北省孟滦林场落叶松白桦混交林直径结构分析[J].河北林果研究，2012，27（4）：375～379.

[13]王香春，张秋良，春兰，等. 大青山落叶松人工林直径分布规律的研究[J].山东农业大学学报：自然科学版，2011，42（3）：349～355.

[14] 李梅.刘广营，兰永，等. 新丰林场华北落叶松人工林的直径结构分析[J].河北林果研究，2012，27（3）：245～248.

[15] 王俊峰，欧光龙，陈金龙，等. 基于理论生长方程的云南松火烧迹地幼龄林林分直径结构[J].中南林业科技大学学报，2013，20（4）：49～52.endprint