浅议第二价格密封招标在铁路通用物资招标采购中的适用性
刘曾亮


摘要:指出了铁路在全面实施公开招标和最低价评标法后,在通用物资方面,投标人为取得价格竞争优势从而降低产品质量和中标后不履约。第二价格密封招标采取最低价投标人中标,次低价作为合同价,在这一博弈模型下,投标人的最优报价为其成本价。这一模式不仅便于招标人发现价格,而且对投标人存在竞争与激励相容,在铁路的招标采购中具有适用性。
关键词:招标博弈模型;等价收入;第一价格密封招标 ;第二价格密封招标;竞争与激励相容
中图分类号:F284
文献标识码:A文章编号:1674-9944(2014)12-0274-03
1引言
自2012年铁道部(现铁路总公司)要求“规范管理 强力推进 全面实施铁路物资公开招标采购”以来,各铁路局采用经评审的最低价评标法,大力推行公开招标,在加大竞争力度、降低采购成本、规范采购行为方面有了较大的提高和改善。然而在不少通用物资的招标采购中,由于最低价中标的导向,投标人不思产品质量的提高反而“挖空心思”将质量控制在最低标准甚至隐性降低产品质量,以期在价格上取得竞争优势,投标人恶性竞争和中标后履约不积极的倾向日益强烈。
在不改变公开招标和最低价中标的前提下,从招标人效用不减和对投标人竞争与激励相容的角度来考虑,第二价格密封招标可以更好地适用于铁路通用物资的招标采购中。下面我们不妨通过招标博弈模型来对第一价格密封招标和第二价格密封招标的投标策略进行分析比较。
2招标博弈模型
2.1招标基本类型简介
招标方式根据拍卖方式演化主要有4种:降价招标(又称英式招标,类似竞价采购)、升价招标(又称荷兰式招标)、第一价格密封招标和第二价格密封招标(又称维氏招标),常用的主要是后两者。在第一价格密封招标中,各投标人不知道其他人的报价,每一投标人单独提交其报价,出价最低的投标人中标,中标合同价为该中标人的报价(即第一价格)。第二价格密封招标与第一价格密封招标不同的是出价最低的投标人中标,但中标合同价为次低者的报价(即第二价格)。
2.2招标模型的假设
(1)投标人是理性经济人,即具有充分考虑自身的局势和投标人之间行为相互的影响,并作出自身利益最大化行为的能力。
(2)独立私人价值,即每一个投标人只知道自己投标物资的价值,这一价值是该投标人的私人价值,其他投标人不知道,但是每一个投标人都知道互相的价值独立取自于某一个区间,并具有相同的密度函数和分布函数。
(3)所有的投标人均为风险中性,即不会低于自己的价值投标。
2.3招标模型的表示
假设有n个投标人竞争一个不可分的标的物。该标的物对投标人i的价值为vi(也可理解为成本加上必要的利润),且这一价值为私人信息,但所有投标人均知道vi取自区间[v- , v+]上具有密度函数f(v)的相同均匀分布F(v)(从而f(v-)=0,f(v+)=1)。所有投标人都是风险中性的。每个投标人的密封报价为bi,且所有的报价bi是关于vi的一个递增函数b(v),即价值越高,报价越高(这也是符合常理的)。为计算方便假设也不存在报价相同的投标人,则在第一价格密封招标中,投标人的收入为:
Пi=bi-vi当bi 0当bi>minj≠ibj时 其中j表示除投标人i外的所有投标人。很显然,当投标人的报价b为n个投标人中的最低时,其中标,收入为其报价减去其私人价值(可理解为成本);当投标人的报价高于任何一个其它投标人时,则不能中标,所以收入为0 。 在第二价格密封招标中,投标人的收入为: Пi=minj≠ibi-vi当bi 0当bi>minj≠ibj时 与第一价格密封招标的不同是中标人的收入为次低价减去自己的价值。 2.4收入等价原理 迈尔森(1981)和赖利、塞缪尔森(1981)几乎同时证明:在给定投标人数,假定所有投标人都是风险中性的,各投标人的价值都相互独立取自同一严格递增的连续分布。那么,任何满足下列两个条件的招标机制都会产生相同的期望收入[1]。 (1)标的物总是为最低价的投标人获得; (2)任何投标人报价最高,那么他的期望剩余为零。 (由于国际上采用博弈分析类似招标问题是从拍卖开始,而且国际上的拍卖包括我国理解的拍卖和招标两种形式,实质上拍卖方是卖方、投标方为买方的拍卖和拍卖方是买方、投标方为卖方的招标之间没有任何正式的区别,本文在引用文献资料时直接将拍卖引用为招标。) 3第一价格密封招标的投标分析 由均匀分布可知:n个独立取自区间[v-, v+]上的均匀分布的随机变量的第k高值的期望值为v-+[ (n+1-k)/(n+1)]( v+-v-)[2] 。 投标人在获胜期望的情况下,其对标的物的价值vi一定是最低价值即bi ui=bi= vi + (1/n)( v+ - vi) 其收入为: Пi=vi+(1/n)( v+ -vi)-vi= (1/n)( v+ -vi) 从上面的投标报价分析看,投标人期望中标,其最优报价取决于参与投标竞争的人数,投标人数越多,其报价越低,当n无穷大时,其报价接近于其价值。 实际上,在第一价格密封招标中对于追求效用最大化的投标人,必须考虑所有其他投标人可能出价的信息,包括其他投标人的价值、风险偏好、竞争者的数量。投标人在此最优报价的基础上,降低一些则会增加中标的概率,但却减少中标后的利润。由于缺乏按照自身真实价值报价的激励,在竞争激烈的情况下,投标人“挖空心思”向招标人打探其他竞争对手的信息和将质量控制在最低标准甚至隐性降低产品质量,以期在价格上取得竞争优势的动机就更强烈一些。
4第二价格密封招标的投标分析
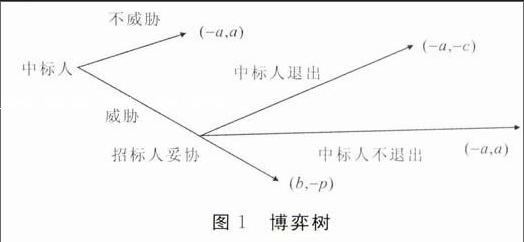
第二价格密封招标的投标策略就简单多了。同样只有在bi Пi=0①当v j-v②当v 0③当j -w④当j 因第④种情况为产生负的收入,投标人不会选择;第③种情况投标人i不会中标,所以收入为零,我们也不加分析。 在第①种情况下,显然投标报价取[v, j) 中的任意数时能中标,都将获得j-v的收入,而取最小值v为最优策略; 在第②种情况下,显然投标报价取[v, b) 中的任意数时,能中标,都将获得j-v的收入,而取最小值v为最优策略; 在第③种情况下,虽然投标报价取[v, b) 中的任意数时,不能中标,但显然最小值v在不影响收入的基础上最优。 通过上述分析,在第二价格密封招标中,无论在何种情况下,投标人的最优策略都是按私人价值报价,即说真话(真实地反映自己的成本价)。投标人的策略不依赖于其他投标人的数量、私人价值、风险偏好等。在说真话的最优策略下,还能够得到招标人的奖励(以次第者的价值作为合同价,确保有利可图)。而招标人不仅可以掌握标的物的行业真实成本情况,还可以因中标人有适当的利润而减少不履约带来的风险。 5第二价格密封招标方式的改进措施 5.1第二价格密封招标方式缺陷的改良设计 很多经济学家的研究结论显示:虽然根据收入等价原理,第二价格密封招标与第一价格的密封招标的期望收入是等价的,但是其方差却相对较大,而且在投标人的风险偏好不一样和投标人价值区间不同的情况下,第二价格密封招标较之第一价格密封招标在招标人的收入上会带来较多些的风险,而且投标人在第二价格密封招标比第一价格密封招标中串谋的动机更大一些。 我们可以通过扩大竞争力度和设置保留价来降低这些不利因素所带来的影响。通过扩大竞争力度,在投标人数增加的情况下,一方面可以缩紧投标人私有价值的区间密度,缩小最低价与次低价的差别区间;另一方面可以增加投标人串标的难度和成本,投标人多了,串谋的难度就大了,串谋的成本就高了。招标人设置合理的保留价也可以起到扩大竞争力度同样的效果。中标人的报价不仅是所有投标人中的最低报价,还要低于保留价,当保留价是次低价时,保留价将作为合同价,这样也可以缩小最低价与次低价的差别区间,而且投标人要想通过非正常途径中标,不仅要与其他投标人串谋还需要与招标人串谋,这将大大加大了串谋的难度和成本。 5.2第二价格密封招标方式中标人不履约的防范措施 部分投标人恶性竞争,企图通过低于成本价中标,而后威胁招标人给予调价补偿,于是就出现图1的博弈。 图1博弈树 如果中标人实施威胁调价后,招标人在不妥协的情况下的损失c要大于妥协的损失p,招标人就会选择妥协,而投标人调价后会获得b+a的额外收益,在此种情况下,中标人就会不履约。这一博弈树清晰反映了中标人不履约的动机来源有两个:一是违约带来额外利益(即惩罚不够);二是中标人违约的损失小于招标人重新采购带来的损失。 因此招标人可以一方面加大对违约的惩罚力度(如加收履约保证金、限制后期投标等),一方面尽量减少投标人违约造成的损失(提高应急库存、选取多个中标人等)。由于第二价格密封招标的中标人具有一定的利润激励,这将会降低中标人违约的风险。 由于通用或是其他行业供应者较多物资具备充分竞争的条件,采取第二价格密封招标的激励相容的招标方式不仅可以取得与第一价格密封招标相同的期望收入,还可以发现价格,激励投标人理性竞争,降低了中标人违约的风险,应该说第二价格密封招标在铁路招标采购中具有一定的适用性。 参考文献: [1]Vijay Krishna(美).拍卖理论[M].胡军,张聪,译.上海:上海人民出版社,2012. [2]Paul Klemperer(英).拍卖:理论与实践[M].钟鸿钧,译. 北京:中国人民大学出版社,2006. [3]候 强,沈玉志.两种密封招标采购的对比分析[J].科学与技术工程, 2005,5(8):529~532. [4]杨颖梅,王文举.招标支付等价性及最优保留价博弈分析[J].经济与管理研究, 2007(11):54~58. [5]毛林繁.从经济学角度出发构建招标采购理论体系[EB/OL].政府采购信息网,2012—02—20.

