基于有限增量法的非线性RL电路的研究
彭川来
(闽南理工学院,福建 石狮 362700)
0 引言
非线性电路除了极少数情况外,是无法得到非线性微分方程的解析解,因此本课题采用分段有限增量法求解一阶RL 非线性电路微分方程近似解。对线性和非线性RL 电路暂态过程进行了对比和分析,同时利用Matlab 软件结合实验数据清晰直观的揭示出非线性RL 电路暂态过程的特性。
1 一阶非线性电路暂态过程的分析
1.1 一阶非线性电路
一阶非线性电路只含有一个储能元件(电感或电容),但可能含有多个非线性电阻;而且储能元件可能是线性的,也可能是非线性的[1]。按网络中是否含有时变电源或时变电阻,一阶非线性电路可区分为非自治和自治的两大类。对于非自治的一阶非线性电路来说,其状态方程具有如下形式:

对于自治的一阶非线性电路来说,其状态方程具有如下的形式:

求解一阶非线性电路方程的方法有:直接积分法、数值分析法、图解法、分段线性化法以及有限增量法等。本文将采用有限增量法对一阶非线性电路进行求解。
1.2 有限增量法
在求解非线性电路暂态过程中,关键的一步是求解积分。由于非线性电路元件的特殊性,直接积分往往得不到解析结果,这就需要采用近似方法求解。
有限增量法是一种利用微分方程的数值求解法来求解非线性电路的暂态方程的方法。其要点在于将要研究的其中过程的全部时间化为许多微小的间隔Δt 过程,从而把微分方程中的微分量近似的用增量代替。
2 线性电阻和非线性电感组成的一阶非线性RL 电路
2.1 非线性电感L 的特性的测量[2]
实验仪器为磁滞回线实验组合仪(TH-MHL 型磁滞回线实验仪)、非线性电感L、示波器,实验原理见图1。
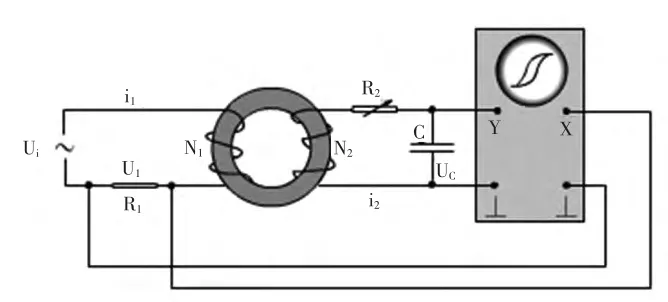
图1 测量动态磁滞回线电路图
测出不同输入电压下的磁滞回线的饱和点的H 和B,即可得到起始磁化曲线。其中N1=50,N2=150,R1=2.5Ω,R2=10kΩ,C=10μF,L=60mm,S=80mm2。
利用Mtlab 可画出非线性电感的H-B 曲线图。对于面积为S、匝数为N、磁感应强度为B 的电感其磁通量:Ψ=NΦ=NBS。而磁场强度H=NI/L,则:I=HL/N。非线性电感线圈磁通量随电流的增大而增大,而后逐渐趋于稳定,因此磁通量Ψ 可拟合为电流的幂级数,且幂数n应小于1。利用Matlab 拟合工具可得Ψ—i 拟合曲线,见图2。
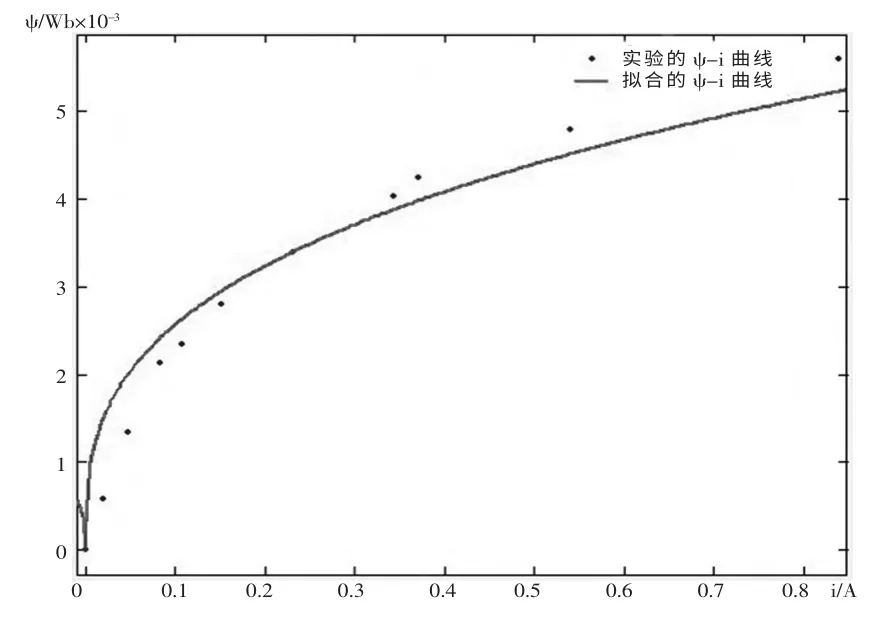
图2 拟合后的Ψ—i 曲线
2.2 非线性电感的一阶非线性RL 电路的研究
应用Kirchoff 定律:

其中:ε—稳压电源输出的电压;μL—电感两端的电压;uR—线性电阻两端的电压。而,Li随电流的变化而变化。
(1)非线性电感的一阶非线性RL 电路暂态过程的实验。实验中用信号发生器的方波输出信号作为电路中的输入电压,将示波器S 的接在电感两端用以测量电感两端的uL-i 关系。实验电路见图4。
(2)非线性电感的一阶非线性RL 电路暂态过程的解[8]。非线性电感的韦安特性为:

图3 非线性电感的RL 电路图
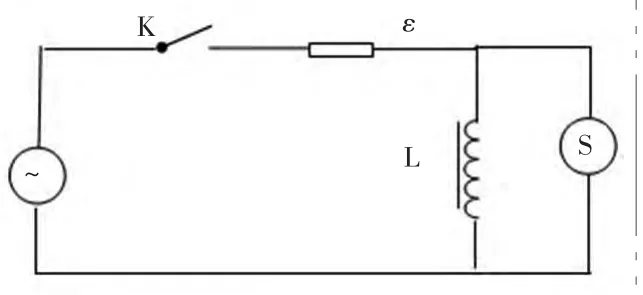
图4 非线性电感的RL 电路测量图




分离变量求解分后可得:

代入初始条件x(t=0)=0 后可得:

同理对于放电过程:

代入初始条件x(t=0)=1 后可得:

式(9)只给出了充电过程中,电流与时间的关系式,却无法得出i-t 曲线图或UL-t 图。为了得到电感两端的u-t 曲线图,采用有限增量法求解。对于电阻R=100Ω,输入电压ε=2.0V 的电路,其电路方程为:

把此方程近似的写为:

时间间隔取△t=0.02ms,可得表1 的有限增量法求解数据。因此可得到R=100Ω 下的理论曲线和实验曲线见图5。
非线性电感的RL 电路电感两端电压刚开始变化比较缓慢。电感两端的电压随时间的变化比较均匀。
放电过程一阶非线性RL 电路的uL-t 曲线。根据式,而,将i0=0.02A,R=100Ω 代入可得图6 的曲线。与图5 不同,放电过程非线性电感两端的电压刚开始变化很快,而后慢慢趋于零。放电过程与充电过程的规律不同。

表1 有限增量法求解数据

图5 R=100Ω 的非线性电感两端的理论曲线和实验曲线
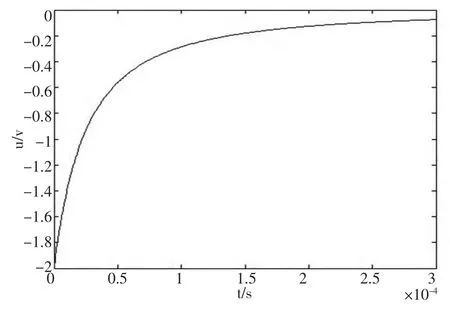
图6 R=100Ω 的非线性电感两端放电u-t 曲线
3 讨论
(1)与线性RL 的电路按的规律变化相比,非线性RL电路充放电从图5 和图6 可以看出遵循着完全不同的规律,充放电曲线为不均匀曲线。
(2)由式(6)、(9)和(11)可得:
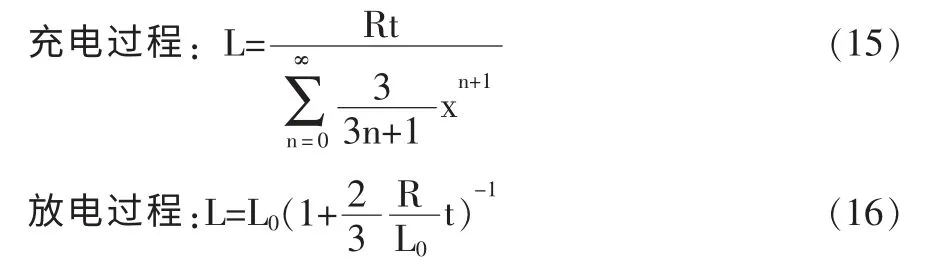
(3)与非线性电阻的一阶非线性电路类似,非线性电感的RL 电路里,τ 不是一个常数。但是,在一个无限小的充放电过程,L/R 可近似为一个常数,不妨称之为非线性RL 电路暂态过程中的瞬间时间常数。瞬间时间常数是衡量一个无限小暂态过程充放电快慢的标志,也就是说, 一个有限大小的非线性电路的暂态过程是由一系列无限小线性暂态过程组成的。
(5)与线性RL 电路类似,非线性RL 电路中,存在电阻越大,其充放电速率越快;电阻越小,其充放电速率越慢的现象。
[1]夏承铨.电路分析[M].武汉:武汉理工大学出版社,2006.
[2]邓金祥,等.大学物理实验[M].北京:北京工业大学出版社,2006.
[3]符五久. 非线性电感电路的暂态特性[J]. 大学物理,1997,9.

