面向铁水温度的高炉异常数据检测及修补

赵 哲，张 勇，于楠楠，崔桂梅

（内蒙古科技大学 信息工程学院，包头 014010）

高炉冶炼是一个持续性的高温生产过程，高炉的稳定顺行是一切生产技术经济指标和良好的经济效益的基础[1]。炉温是高炉稳定顺行的一个重要指示，在高炉冶炼过程中，一直以化学热［Si］（高炉铁水硅含量）来表征炉温，一定时期内对于指导高炉操作具有积极的作用。但由于炉况的波动，炉况非平稳时会出现高硅、高硫及低炉温的现象[2]，再利用铁水硅、硫含量这种传统方法去表征高炉炉温是不准确的甚至是与实际相反的。随着测量手段的发展铁水温度测量数据的获取和存储已在各大高炉得到了广泛的应用，以铁水温度表征炉温的物理热的形式也越来越受到了炉长们的关注。

铁水温度除了表征高炉炉温以外，还是影响高炉出铁和出渣的重要参变量，铁水温度过高或过低都不利于出铁和出渣。而现行的高炉操作是以炉长为主的人为操作制度，铁水温度数据受人为因素、测量环境变化等影响容易出现数据缺失及记录异常。这些异常数据的存在，使得通过铁水温度观测炉温，反映炉况运行状态及指导高炉操作变的比较困难。

针对数据缺失及异常，常规方法主要采取3σ法则进行异常值剔除[3]，并用均值插补法进行数据修补。研究发现采取传统的方法进行异常数据处理则有可能造成数据的填充不准确或正确数据被误剔除的现象。在数据检测上本文首先针对数据样本进行常规的数学统计，确定均值、方差及问题数据的时间点，进而从多尺度[4]的角度对问题数据的时间点采取短时间序列[5]的重新组合、统计及计算。在数据修补上，结合AR模型[6]对缺失值插补，并考虑数据本身的特点。最后，以某钢厂高炉数据做模型试验，结果表明本方法比常规方法具有良好的检测效果及修补优势。

1 高炉数据检测及修补问题

现行的高炉操作是以炉长为主的人为操作制度，高炉数据受人为因素、测量环境变化等影响容易出现数据记录异常。如表1所示536批铁次的铁水温度明显是异常数据；而表2第1032批铁次铁水温度缺失则是受人为或仪器故障造成。如何更精确地检测到异常数据，并还原数据，让以数据为基准的高炉操作更具可操作性，是高炉建模、优化及操作面临的首要问题。

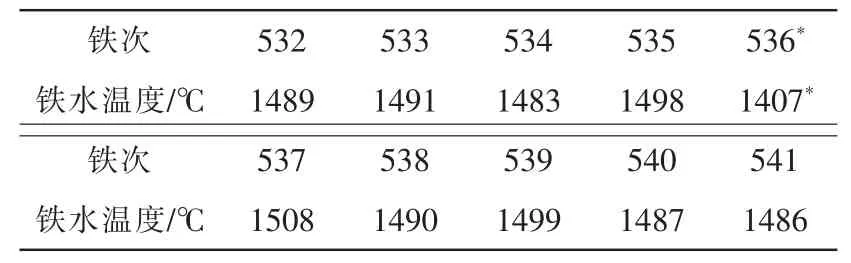
表1 铁水温度异常Tab.1 The Thm abnormal

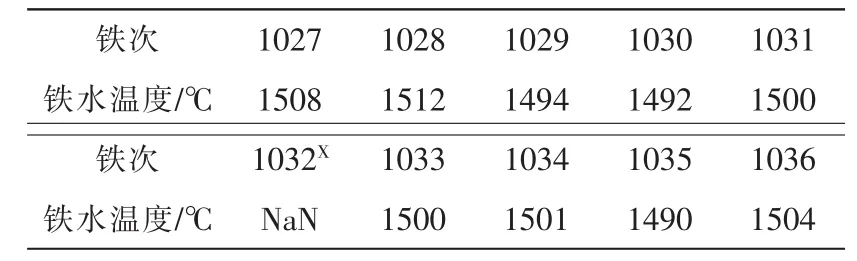
表2 铁水温度缺失Tab.2 The Thm missing

1.1 异常值监测

常规异常值检测主要采用3σ法则，在3σ法则中σ表征标准差，μ为均值，以某钢厂高炉铁水温度3000组数据为例，计算得其均值μ＝1493，标准差σ＝12.71。由3σ法则对于值不在内的概率小于0.3%既认为其为异常值，可找到其异常值位置并对其进行剔除。现对某钢厂3000组铁水温度进行检测，发现表1中的第536批铁次的异常值被正常剔除，其结果如图1所示。但遇到表3中第853、854、855批铁次由于高炉在停炉、休风、检修及开炉时，炉况波动较大，数据变化也大，常规3σ法则无法判断其铁水温度下降原因，从而导致正常值被误剔除，其结果如图2所示。正常数据被误剔除给高炉后期的建模、优化及操作带来不利影响。所以针对高炉这种高度复杂系统采用传统3σ法则进行数据异常值检测是不合理的。

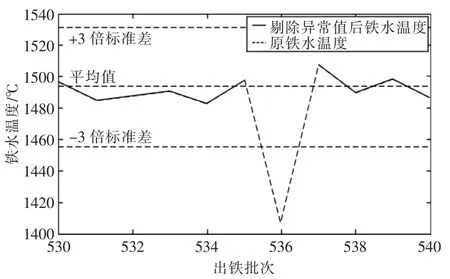
图1 铁水温度异常值被剔除Fig.1 Reject abnormal data of Thm

图2 铁水温度正常值被剔除Fig.2 Reject normal data of Thm

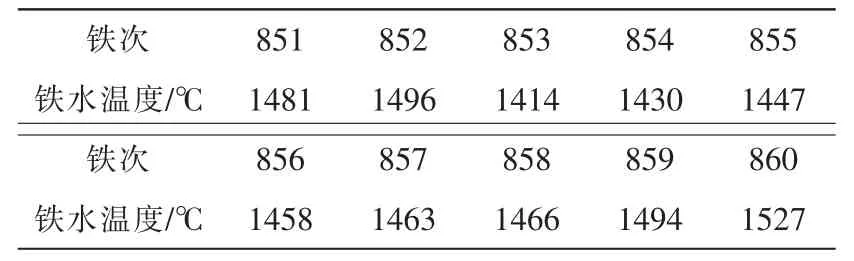
表3 铁水温度正常Tab.3 The Thm normal

1.2 缺失值补值

常规缺失值补值主要采取均值插补法[7]。由于高炉冶炼是一个持续性的高温生产过程，其铁水温度前一时刻与后一时刻均相互关联，因此利用均值插补法进行补值是合理的。首先确定铁水温度缺失位置，然后以其前一时刻的铁水温度与最近的下一时刻铁水温度求均值，最后对缺失位置进行补值。现对于表2中的第1032批铁次缺失值可以利用均值插补法进行补值，但如遇到由仪器长时间故障造成铁水温度连续缺失，显而易见，简单地利用均值插补法对连续缺失的数据进行补值则是不合理的。

2 数据检测及修补新方法

针对传统异常数据检测及修补方法对于高炉这种高度复杂的系统的不合理性，现结合高炉数据本身特点提出新的解决方法，为节能型高炉建模、优化及操作提供更为真实的数据。

2.1 基于多尺度的异常值检测及修补

由于常规异常值检测3σ法则存在无法准确区分数据超出μ±3σ范围外的问题，既当高炉正常休风维护时造成的铁水温度正常下降超出μ±3σ范围时，被误当做异常值给剔除的问题。现结合高炉数据本身特点引入多尺度与常规3σ准则相互结合来判断铁水温度超出μ±3σ范围是否由异常值引起的。

尺度是空间数据的共有特征，同时人们对数据的观测及判断也是在不同尺度上进行的。因此用多尺度来描述、分析数据是非常自然的事情[8]。

多尺度与传统3σ法则结合，先用粗尺度对数据共性进行认识，再进行尺度变换以细尺度对数据个性进行认识，最终通过尺度变换达到对数据的准确认识，如图3所示为其检测流程图，针对铁水温度异常值检测具体步骤为

步骤13σ法则对整个样本空间进行粗尺度异常值检测，找到μ±3σ外铁水温度的铁间批次Tn；

步骤2以Tn为中心与n-1、n+1批铁次组成小样本空间对其进行细尺度3σ检测，找到μ1±3σ1外铁水温度的铁间批次 T（1）n，其中 μ1、σ1分别为小样本空间的均值与方差；

步骤3铁间批次T（1）n所对应的铁水温度既判定其为异常温度对其进行剔除。

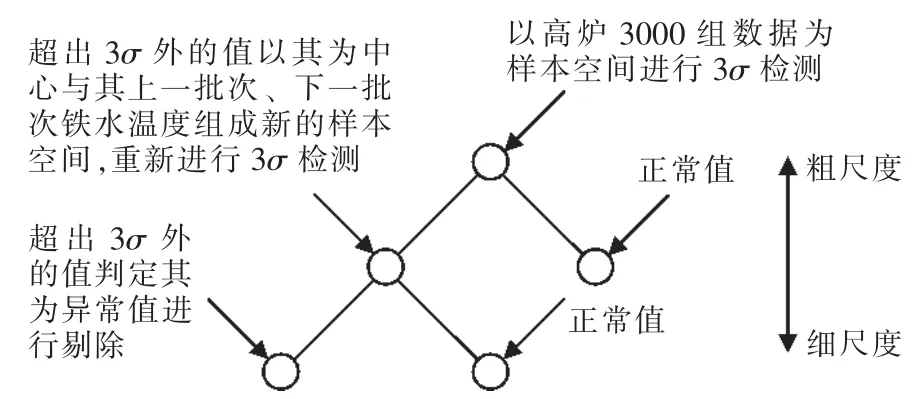
图3 新异常值检测方法流程图Fig.3 New outliers detection method flow chart

2.2 基于AR模型的数据填充

均值插补对于数据的单一缺失值有良好的补值效果，但对于事故造成一段时间内数据连续缺失时再简单的利用均值插补法进行补值会对数据产生较大的偏差，这些偏差较大数据难以反映高炉数据的真实性。

AR模型是数据处理、修补及噪声方差估计过程中常用的模型，其可以通过时间序列的历史数据来体现数据随时间的变化规律，将这种变化延伸到未来，从而实现对数据的预测[9]。既某一时刻的铁水温度可由前几个时刻的数据并依据自回归时间序列模型修复：

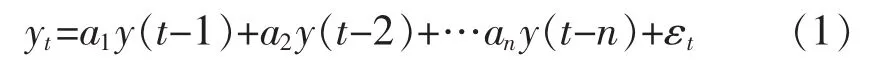
式中：yt为第t批铁次的铁水温度。

考虑高炉数据特点，此处值可由异常数据的前2个时刻数据并依据二阶自回归模型修复，其中ai（i=1，2）为模型参数，由铁次t前的正常高炉炉温样本数据｛y1，y2，…，y（t-1）｝训练可得。

an为第t-n批铁次与第t批铁次相关系数，an用最小二乘辨识方法进行参数估计[10]，普通的最小二乘需要更多的数据对其进行训练，但高炉的复杂性使其数据存在不确定性，不能有效的保证更多的训练数据都为正常数据，对其进行参数估计存在较慢的收敛速度，较低的估计精度，因此在此选用多信息最小二乘方法进行参数估计[11]，即用更少的数据获得更快收敛速度，更高的预测精度。

考虑到t-p+1到t时共有p组数据，令

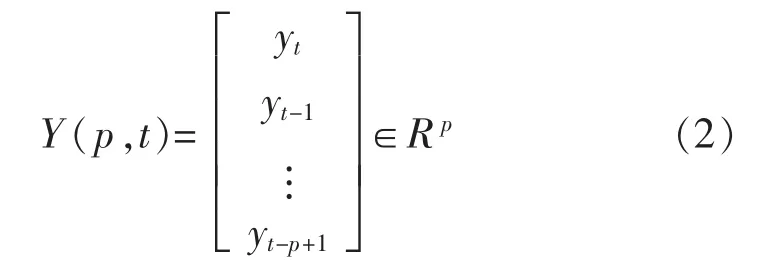
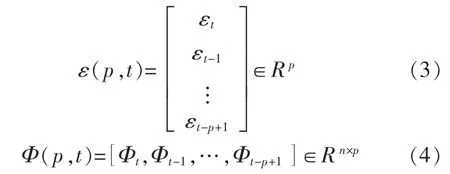
矩阵方程：

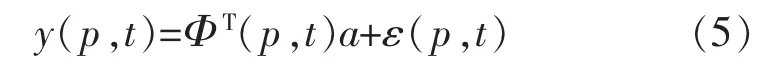
取准则函数：

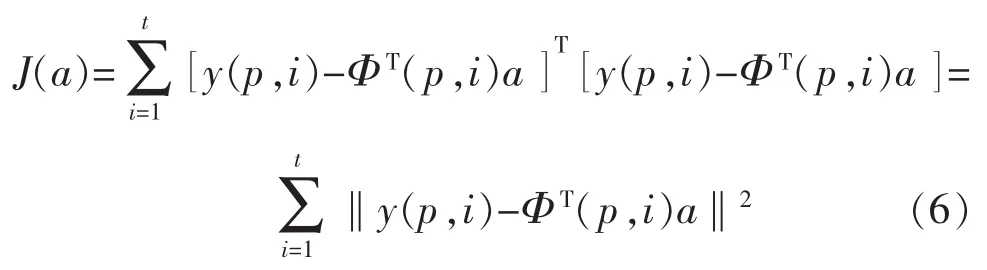
使准则函数最小的多信息最小二乘算法如下：

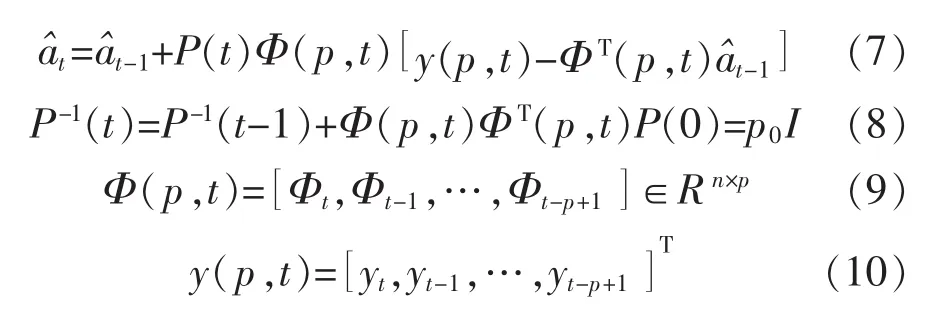
式中：yt∈R为系统输出，a∈Rn为待辨识的参数向量，Φt∈Rn是由系统输入ut∈R和输出Xt构成的回归信息向量，εt为均值为零的干扰噪声。在此用100组数据即可对a进行参数估计。

3 仿真结果及分析

现应用新方法对铁水温度进行检测，其检测结果如图4、图5所示。从图中可看出铁水温度异常值被准确剔除，而由于休风引起的铁水温度正常下降未被误剔除，数据处理结果表明常规准则与多尺度结合针对高炉这种高度复杂的系统可以准确地剔除异常值，并有效地防止高炉因正常维护引起的铁水温度过低被误剔除。

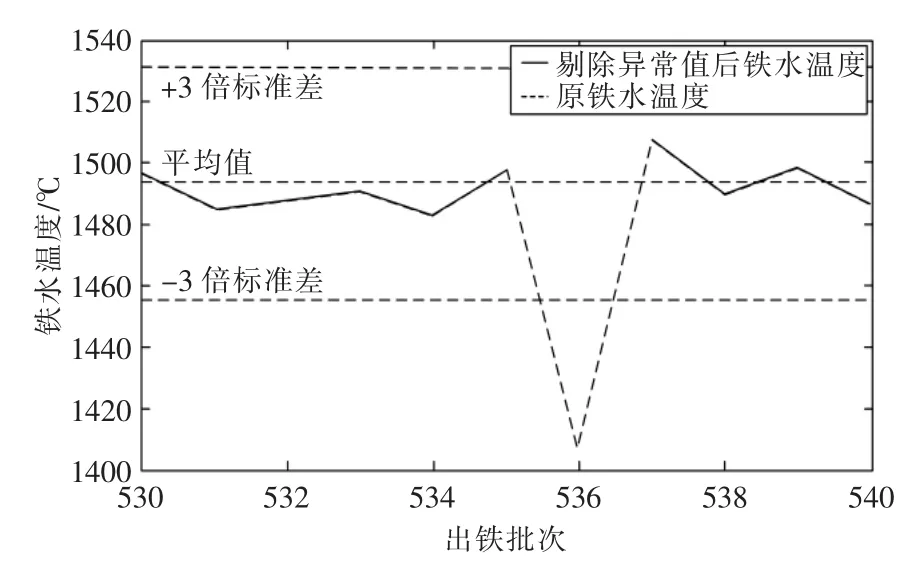
图4 铁水温度异常值被剔除Fig.4 Reject abnormal data of Thm

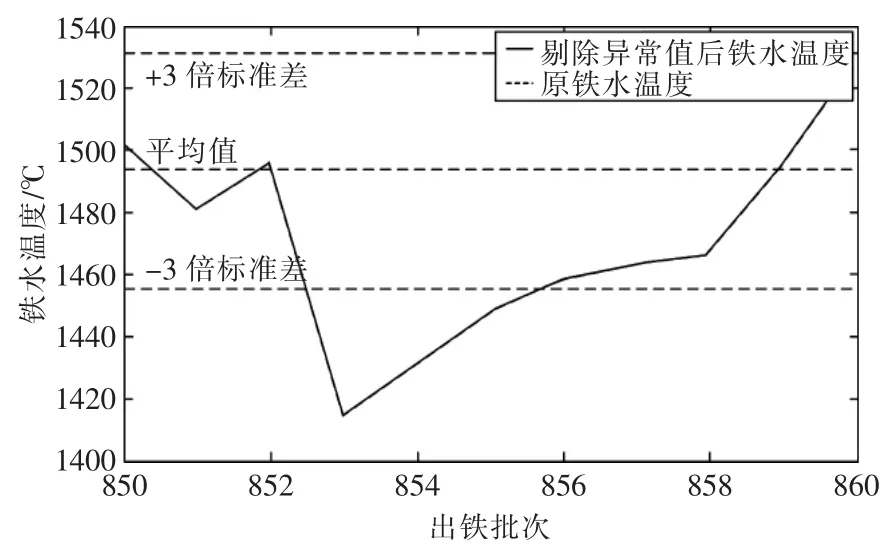
图5 铁水温度正常值未被剔除Fig.5 Not reject normal data of Thm

现人为去除表4中2002～2007批铁次的铁水温度，分别使用常规均值插补法与AR模型对缺失值进行补值，并与原始值进行对比，校验数据修补性能。

表4 铁水温度Tab.4 Data of Thm

现分别对2种补值方法用平均相对误差、最大相对误差、预测精度相对比，结果如表5所示，其中用均方根误差表示预测精度：

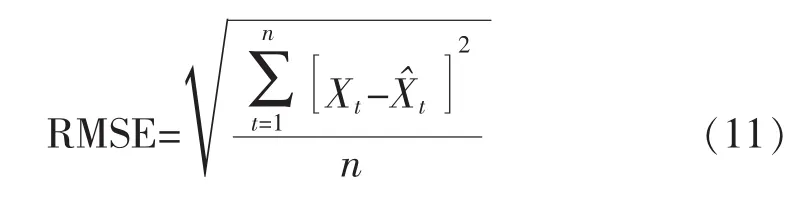
式中：Xt为铁水温度实际值；X^t为预测铁水温度；n为预测样本个数。

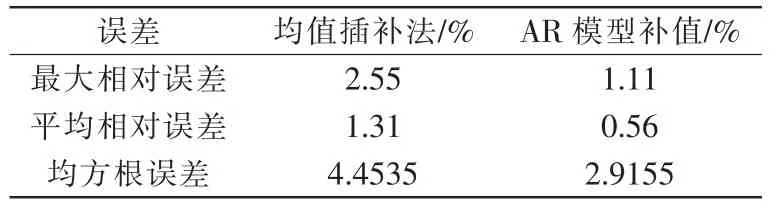
表5 各模型性能比较Tab.5 Model performance comparison

从表5中可以看出AR模型补值的效果优于均值插补法，在铁水温度连续缺失时AR模型也能取得较好的补值效果。

其修补结果如图6所示，图6为2种方法修补后数据与原数据进行对比，从图中也可以明显地看出AR补值相比于传统的均值插补法补值效果更好。

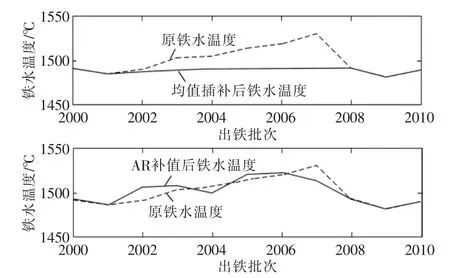
图6 均值插补与AR模型补值对比Fig.6 Comparisons between mean interpolation and AR model process

4 结语

本文针对传统修补方法不适合高炉这种高度复杂的系统的问题，结合高炉本身特点，提出多尺度与传统3σ法则相结合对铁水温度进行异常值检测、异常数据的位修补、基于AR模型的数据修补等新方法。并应用某钢厂数据仿真，数据仿真结果表明，本文提出的新方法可有效地剔除异常值，同时防止正常值被误剔除，补值效果也更接近于实际值，这为后期节能型高炉建模、优化及操作提供了更为真实的数据。

[1]范广权.高炉炼铁操作[M].北京：冶金工业出版社，2008.

[2]周传典.高炉炼铁生产技术手册[M].北京：冶金工业出版社，2012.

[3]桂卫华，阳春华.复杂有色冶金生产过程智能建模、控制与优化[M].北京：科学出版社，2010.

[4]高惠君.城市规划空间数据的多尺度处理与表达研究[D].北京：中国矿业大学，2012.

[5]肖辉.时间序列的相似性查询与异常检测[D].上海：复旦大学，2005.

[6]常太华，王璐，马巍.基于AR、ARIMA模型的风速预测[J].华东电力，2010，38（1）：59-62.

[7]金勇进.缺失数据的插补调整[J].数理统计与管理，2010，20（5）：47-53.

[8]潘泉，张磊，崔培玲，等.动态多尺度系统估计理论与应用[M].北京：科学出版社，2007.

[9]胡劲松，杨世锡.EMD方法基于AR模型预测的数据延拓与应用[J].震动、测试与诊断，2007，27（2）：116-170.

[10]彭秀艳，王茂，刘长德.AR模型参数自适应估计方法研究及应用[J].哈尔滨工业大学学报，2009，41（9）：12-16.

[11]丁锋.系统辨识[J].南京信息工程大学学报：自然科学版，2012，4（1）：1-28.