基于Shapley模型的公私合营基建项目股权结构研究

马若微，王召方

(北京工商大学 经济学院，北京100048)

一、引 言

依据项目区分理论，按照主营业务的不同，基建企业能够细分为公益性基建企业(业务涉及环保环卫、防卫防灾、市政服务等领域)、准经营性基建企业(业务涵盖电气水热供给，电讯邮政等方面)以及经营性基建企业(业务包括收费道路桥梁建设运营等内容)。随着城镇化的进一步发展，我国城市基础设施建设的规模日益扩大，所需资金规模巨大，仅依靠政府财政资金，难以为继。为解决其融资问题，针对准经营性基础设施建设，公私合营模式被广泛应用。而在其实务运作过程中，股权结构成为一个关键问题。

公私合营企业由于政府资本的普遍参与，其在项目的风险分配和风险控制方面与普通企业存在较显著差异，其股权结构具有本身的特性，针对此问题目前理论界鲜有研究，而在实务操作中，目前所见案例都是以专家评估以及借鉴类似项目的方式来确定股权结构中的政府资本与民间资本比例，这样的操作较易导致高昂的成本。

本文将公私合营项目中政府资本和民间资本的共同参与看作一种合作联盟，运用Shapley模型思想，计算参与各方在不同建设方式下对成本的节约，量化其对项目的贡献程度，确定未来项目收益的各方分配比例，进而确定各方期初投入资本占总资本的比例。本文结构大致如下:第一部分为引言与文献综述，第二部分为基于Shapley模型的公私合营项目合作博弈分析，第三部分是基于各方贡献程度的模型构建，第四部分是结合陆港T项目所进行的案例分析，第五部分是研究结论。

二、文献综述

按照本文的研究思路:不同的风险分配和风险控制会导致综合成本不同，而成本的差异即贡献程度的不同会最终决定各投资方投入资本的比例。因此，我们将已有文献按照以下两个部分进行梳理:其一是关于风险分配和分担问题的研究，其二是关于股权结构的研究。

项目风险分配及分担问题:Obaid最早使用人工神经网络法对公私合营项目中的各种风险进行了识别[1]。刘新平、王守清等人定性研究了风险分配问题，他们从风险分配功能角度得出了项目风险分配的三个基本原则，并设计了公私合营项目的风险分配框架，即风险初步分配、全面分配、跟踪和再分配三个阶段[2]。杨秋波、侯晓文等人进一步研究了风险的定量分配，他们运用马柯维茨模型证实了存在公共部门和私营机构风险分担的最佳比例，使得PPP 项目整体风险最小[3]。Xiao-Hua Jin、Guomin Zhang建立、训练、验证和测试了风险分配决策的人工神经网络(ANN)模型，培训和评价结果表明相对于传统的多元线性回归模型，人工神经网络模型能取得令人满意的风险分配决策过程[4]。有一些国外学者考虑了项目风险对项目综合成本的影响，其中:Robert L.K.Tiong等人对整个运行周期的成本进行了计算，把利率、项目期限等对项目产品价格调整有影响的因素代入，得出不同状况时项目的整个成本[5];Michel J认为项目风险分担对项目总体成本的影响归结为生产成本效应、交易成本效应和风险承担成本效应三个效应，即风险分配从三个角度影响着项目总体成本[6]。

项目股权结构的研究:国内学者较多的是定性方式研究公私合营项目股权结构:孙慧、范志清、石烨运用非合作博弈的模型和方法，研究了公私合营模式下政府和私营财团对于新建一条高速公路项目中的最优股权结构问题[7]。盛和太、叶晓甦等从公私合营项目控制权的角度，深入探讨了项目控制权的本质，认为公私合营项目控制权实际上是资源基础上的企业控制权，包括实质控制权和剩余控制权，是公共项目公私合作模式的基础[8]。随着研究的推进，有少量学者尝试以定量方式对股权结构进行确定:刘宇文、王永清在权衡理论的基础上引入Leland模型，该模型以公司权益、公司债务的价值和公司资本结构的关系作为基础，通过加入公司风险、无风险利率等变量分析各种情况下的资本组成问题[9]。Antonio Dias、Ioannou基于资本资产定价模型(CAPM)估计特定项目的净现值(NPV)和权益回报率(ROE)，以 ROE为目标函数，来推导最优资本结构债务和权益资本比例[10]。

根据以上对国内外文献的梳理，我们发现已有研究为本文深入分析奠定了理论基础，但同时也呈现出以下问题:

现有公私合营项目股权结构研究较少考虑风险因素。公私合营项目中，不同参与方其风险的分担和控制能力不同，不同的参与方式会导致项目整体成本出现显著差异，因此在确定项目股权结构时必须考虑风险因素，而目前关于股权结构的研究还鲜有对项目风险的定量分析，这种情况在一定程度上会导致该方向研究缺乏依据和可信性。

公私合营项目股权结构的确定方法有待进一步扩展。目前关于公私合营项目中股权结构的研究处于初步探索阶段，多通过定性分析传统公司资本结构来确定股权结构，忽略了公私合营项目其股权结构的特殊性，分析方法也有待改进。

基于上述分析，本文将博弈论中的Shapley模型应用于公私合营项目股权结构的确定，试图将风险因素纳入到项目成本中，通过估算不同参与方式下的成本节约，计算各参与方的投资收益分配以及投资占比。

三、公私合营合作博弈的Shapley模型分析

(一)合作博弈的Shapley模型特性

Shapley值法是 Shapley L.S.于 1953年提出的用于解决多人合作时收益分配问题的一种数学方法。当n个人从事某种经济活动时，对于他们之中若干人组合的每一种合作形式，都会得到一定的效益，当人们之间的利益活动非对抗性时，合作中人数的增加不会引起效益的减少，这样，全体n个人的合作将带来最大效益，Shapley值法是分配这个最大效益的一个解决方案。它的出发点是根据联盟中每个成员对联盟的边际贡献分配联盟的总收益，以确保分配的公平性，且Shapley值具备以下性质:

①集体理性:在合作博弈联盟(N，v)中，当且仅当每位博弈者所分得的收益的总和等于联盟的总收益时，则收益支付向量 xi=(x1，x2，…，xi，xN)符合集体理性。

②个体理性:在合作博弈联盟(N，v)中，当且仅当每位博弈者所分得的收益都大于其不参与该联盟时的收益时，则收益支付向量 xi=(x1，x2，…，xi，xN)符合个体理性。

③唯一性:根据Shapley值的计算公式:

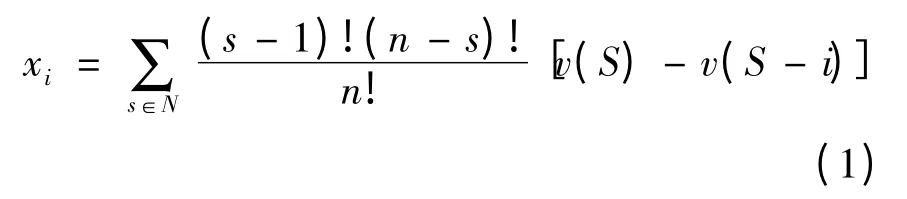
可知，在任何博弈中进行的运算都可以得到一个结果，并且这个结果是唯一的。

Shapley值可满足以上三条性质，此时合作联盟是稳定的、可持续的[11]。

(二)公私合营模式中参与各方利益关系分析

对于某项基础设施建设项目而言，若政府方面单独建设，其面临着效率低、管理成本高、专业化程度不高、对建设期间的设计与建设风险控制不足等各方面的劣势，这势必会造成该项目较高的成本;若由民间资本单方面建设，则面临着对其自身来说控制力度很弱的政治、经济、法律方面的不确定性，为了控制或者规避这些风险，民间资本必然加大对这些不确定性的控制，进而导致项目成本的上升。而针对该类基础设施项目而言，若采用公私合营模式，则可以发挥政府方面和民间资本各自的优势，弥补各自的不足，进而较大幅度的降低项目的综合成本。例如，政府方面对政治、宏观经济、法律及社会方面的不确定性的控制和承受能力较强，在公私合营项目中，这有利于降低整体的不确定性和成本;民间资本则具备较强的设计施工优势、成本节约和管理高效等一些方面的优势，在公私合营项目中由民间资本发挥其优势，也会降低整体成本。

(三)Shapley模型在确定公私合营项目股权结构的适用性分析

根据对公私合营模式的分析可知，在公私合营项目中政府方面和民间资本的合作可以看作是一种合作联盟，该合作联盟中首先要解决的就是双方以何种比例决定投入资金。资金边界与收益分配比例的确定，必须保证参与方各自利益目标的实现，至少在这个合作联盟中得到的收益要高于各自独立建设该项目的收益，这样才有可能吸引足够的民间资本参与到公共基础设施项目的建设中来，并实现合作联盟的高效、稳定。这需要充分考虑双方的利益分配，资本投入，是相互博弈、协商谈判的结果，公私合营项目的这种特性，使其更加适合用合作博弈理论的思想来解决股权结构问题。而Shapley值法恰恰是解决合作博弈中收益分配问题的经典方法，所以本文拟应用Shapley值法来探讨公私合营项目股权结构问题[12]。

四、基于参与各方贡献程度的模型构建

(一)模型设计

建模思路就是将成本的节约看作贡献程度，针对同一项目，哪一方能以更低的成本完成该项目的建设，哪一方就该获取更多的收益，相应的就要在公私合营项目中占有较大的股权比重。

设定这个项目不建设时的综合成本为C0;政府单独建设时的综合成本为C1，其节约的成本为C0－C1，则可以将C0－C1看作政府单独建设时的贡献程度;由私人机构单独建设时的综合成本为C2，其节约的成本为C0－C2，则可以将C0－C2看作民间资本单独建设时的贡献程度;由二者合作建设时的综合成本为C3，其节约的成本为C0－C3，则可以将C0－C3看作政府方面与民间资本合作建设时获取的收益。我们要解决的就是根据C0－C1与C0－C2的大小来合理分配C0－C3，进而确定公私合营项目的股权结构。

一般而言，无论是政府单独负责某个准经营性基础设施融资建设的成本C1，还是民间资本单独负责建设的成本C2，其综合成本必然高于二者合作建设的成本C3;而不建设某项目的综合成本C0更高，远大于 C1、C2，所以 C0＞ C1、C2＞ C3，C1与 C2的关系视情况而定。

(二)相关指标分析

下面我们就政府方面单独筹资建设的综合成本C1、民间资本融资建设的综合成本C2、二者公私合营筹资建设的综合成本C3及不建设该项目所承担的社会成本C0进行分析。

准经营性基础设施建设的过程中遇到的风险总体分为两种:宏观风险和微观风险，宏观风险包括政治、宏观经济、法律等政府方面控制力较强的风险;微观风险包括设计、建造、施工、管理等方面的不确定性。对于宏观风险，若由政府方面控制，其控制力较强，则其发生的可能性及发生之后所造成的损失相对来说较小，分别设为r11和Cp1;若由民间资本控制，则其发生的可能性及发生之后造成的损失相对来说较大，分别设为r12和Cp2;对于微观风险而言，若由政府方面控制，其控制力较弱，则其发生的可能性及发生之后所造成的损失相对来说较大，分别设为r21和Cc1;若由民间资本控制，则其发生的可能性及发生之后造成的损失相对来说较小，分别设为r22和 Cc2;这里 r11＜ r12，Cp1＜ Cp2，r21＞ r22，Cc1＞ Cc2。

由政府单独筹资建设时，其资金大多来源自财政资金和银行借款，为了简化分析，我们假定其综合成本包括:投入成本、机会成本及风险发生的潜在损失。其资金中的一部分来源于财政资金，资金投入量即为其投入成本，设为C11;投入这些资金必然减少相对应的利息收入，以r代表实际利率，则由此导致的机会成本为r×C11;对政府方面而言，对于较大的项目，其不可能全部用财政资金，更多的是采用银行借款或者发行城投债及市政债券来筹资，将外部融资额设定为C12，则其相对应的利息支出为r×C12;前述两类风险发生的潜在损失为 r11×Cp1+r21×Cc1;综述，由政府单独筹资建设时，其综合成本:

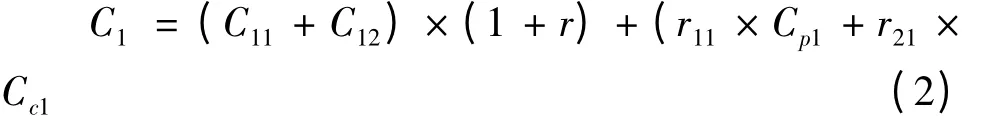
由民间资本单独建设时，假定其综合成本包括:投入成本、机会成本及风险发生的潜在损失。其资金基本来源于自有资金和银行借款或者发行债券筹集的资金，不论是自有资金还是借款，其投入资金所导致的机会成本都是实际利率r与C21投入资金的乘积，即r×C21;前述两类风险发生的潜在损失为:r12×Cp2+r22×Cc2;则其综合成本为:

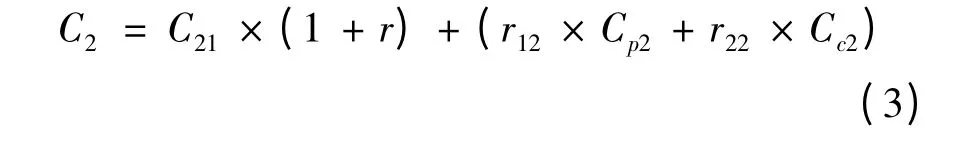
由政府部门和民间资本合作，采用公私合营模式来筹资建设某项目，其综合成本也包括:投资成本、机会成本及风险发生的潜在损失。设其投入成本为C31，其中政府部门承担的部分设为 C311，民间资本承担的设为C312;则其机会成本为r×C31=r×(C311+C312);两类风险发生的潜在损失为:r11×Cp1+r22×Cc2，之所以其潜在损失如上式所示，是因为政府部门对宏观风险的控制力较强，由其负责这部分风险，则宏观风险的潜在损失为 r11×Cp1，而民间资本对微观风险控制力较强，由其负责这部分风险，则其潜在损失为r22×Cc2;则其综合成本:

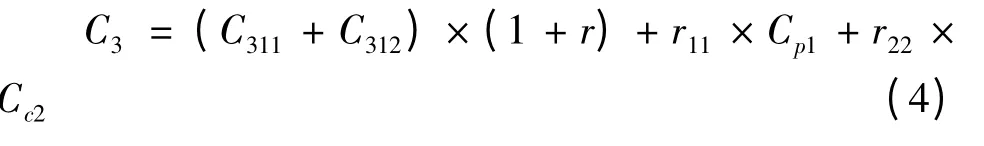
若某项准经营性基础设施不建设，会导致社会经济效益的降低或者丧失提高的机会，本文把这种因不建设该项目所损失的成本称为机会成本，其大致包括:该项目提供的产品或者服务所影响的居民生活水平的改善、该项目的建设带来的经济增长和居民收入水平的提高、居民对政府的满意度等等。由于该项成本对模型的建立和分析并不构成实质性的影响，为了简化分析，我们假定若不建设某项准经营性基础设施而付出的机会成本为C0。

(三)指标数据及调整方法

以上各项成本的分析和设定，是为了模型的建立而结合实际情况设定的，下面我们针对每一项成本，分析其数据来源。

单独由政府方面筹资建设时，(C11+C12)、(C11+C12)×r及(r11×Cp1+r21×Cc1)而言:C11可由与该项目类似的由政府单独建设的项目的单位成本加以调整，然后乘以该项目的数量或者提供产品或者服务的数量来表示。例如:要估算某地铁单独由政府建设时的投入成本，则可选择该地区或者相似地区单独由政府建设的地铁的单位成本，比如每公里的成本，加以调整之后，乘以该地铁项目的里程数，则可以得出该项目单独由政府建设的投入成本(C11+C12)。投入成本估算出来之后，机会成本相对来说就比较容易求得，可用相同时期与该项目资金投入与收回期限相同的银行贷款利率乘以所投入的成本，即可得机会成本r×C11。相对来说较难确定的是(r11×Cp1+r21×Cc1)，本文参照由ANP方法确定的宏观风险和微观风险在项目中的权重来表示宏观风险和微观风险发生的概率r11和r21;而Cp1和Cc1，则作为预估值，可由宏观风险和微观风险发生可能会发生的损失估值表示。

同理，由民间资本或者二者合作筹资建设时，其数据来源大致相同或者相似。

(四)建立基于贡献程度的Shapley模型

由以上分析可知，公私合营项目其实是一个由两个参与者组成的合作联盟，则联盟中的参与者数量[S]=s=2;参与者集合也是两个，即n=2;则根据Shapley值法，对其任意一个参与者而言，其加权因子

若由政府单独筹资建设某项目，所产生的成本的节约为C0－C1，此时就是由政府方面和民间资本组成的联盟S中少了民间资本参与时联盟的特征函数，即v(S－2)=C0－C1，其中v(S－2)中的2表示的是民间资本，v(S－2)表示由政府方面和民间资本组成的联盟在缺少民间资本的参与时的特征函数。

若由民间资本单独建设某项目，所产生的成本的节约为C0－C2，这就是由政府方面和民间资本组成的联盟S少了政府方面的参与时联盟的特征函数，即v(S－1)=C0－C2，其中v(S－1)中的1表示的是政府方面，v(S－1)表示由政府方面和民间资本组成的联盟在缺少政府方面参与时的特征函数。

若由政府方面与民间资本合作筹资建设某项目，所产生的成本的节约为C0－C3，这就是合作联盟S的特征函数，即v(S)=C0－C3。

结合Shapley模型，参与者i的Shapley值:xi=，则在政府方面与民间资本组成的合作联盟中:政府方面(i=1)的Shapley值:

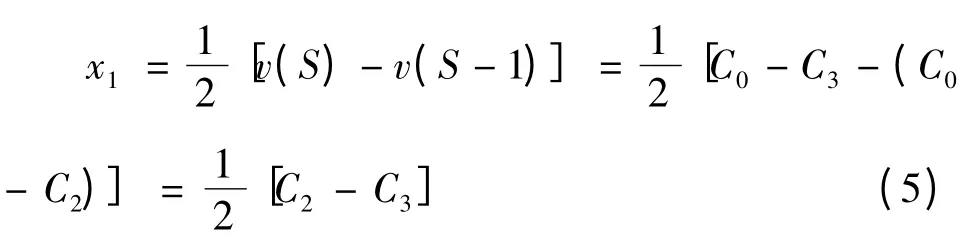
民间资本方面(i=2)的Shapley值:

x1与x2即是因为政府方面与民间资本的分配额度，但其并非最终的分配值，需要做以下调整，用y1表示政府方面对由于二者合作所产生的最终受益的分配比重，则:

同理民间资本对由于二者合作所产生的最终受益的分配比重:

根据前面的论述，可以认为y1与y2就是某项公私合营项目中政府资本和民间资本的股权比例，即公私合营项目的股权结构:y1:y2。

五、案例分析

某港口集团B在国内内陆城市A投资建设陆港T，陆港T项目采用PPP模式由港口集团B与A市政府共同投资建设，其项目计划总投资2.5亿元;如果该项目由政府单独建设，其成本可由具有相似规模的政府单独建设陆港项目的成本来替代，根据相关数据调整之后得出的由政府单独建设的投资成本为5亿元;同样，如果该项目由民间资本单独建设，其成本可由具有相似规模的民间资本单独建设陆港项目的成本替代，根据相关数据调整之后得出的由民间资本单独建设的投资成本为3.5亿元;因不建设该项目所损失的成本对该模型来说只是一个不太相关的变量，我们假定其为7亿元。

根据以上构建的相关变量，在合作博弈模型中，政府的Shapley值:;民间资本的Shapley值;则根据上式可得二者最终受益分配的比重分别为:政府方面、民间资本，即收益分配比重y2:y1=2:3;则相应的该项目的股权结构为:y1:y2=2:3≈0.67。

在合作博弈的Shapley值中，最终的分配结果具备三条性质:唯一性、集体理性、个体理性，因为最终结果的数值已经确定，故唯一性已经满足;该项目收益的分配是按照各自的分配比例确定的，所以其和必然等于总体收益，所以集体理性也满足;以下阐述个体理性。

该项目由二者合作建设的成本为2.5亿元，不建设该项目损失的成本为7亿元，因为我们设定成本的节约看作收益，所以二者合作建设产生的收益为4.5亿元;根据上述结论，可知政府方面分得的收益为1.8亿元，民间资本分得的收益为2.7亿元。

对政府方面来说，政府投入该项目的资本按照上述结论可求得为亿元，由其单独投资时的投入成本为5亿元，则合作建设该项目时可节约出4亿元投入其他项目，这部分资本可取得社会平均的资本回报，按照2010年该项目开始建设时有关学者测算的我国平均的资本回报率15%计算当年的资本回报，可得其三年建设期内的资本回报为3×4×15%=1.8亿元;即政府方面因为参与公司合作建设该项目获得的收益为1+1.8=2.8亿元;而其单独建设该项目是的收益为7-5=2亿元;显然政府方面在参与该公司合作项目时获得的收益2.8亿元大于其单独建设该项目时的收益2亿元，满足了个体理性。

同理，对民间资本而言，可求得其单独建设该项目时的收益为3.5亿元，与政府方面合作建设该项目获得的收益为 2.7+(3.5-1.5)×3 ×15%=3.6亿元，即参与公私合营获得的收益大于其单独建设该项目的收益，满足个体理性。

综上，运用该方法计算出来的收益分配比例满足唯一性、个体理性和集体理性，该合作是一个稳定的合作博弈，可以此来确定二者收益的分配比例，进而确定公私合营项目中的股权结构。

在该项目实例中，其真实的收益分配为政府方面分得收益2.8179亿元;民间资本分得的收益5.1079亿元;二者的比例y1:y2=2.8179:5.1079≈0.56;其与运用本文的方法得出结论的差异处于可以接受的范围内。

六、结 论

本文深入分析了公私合营项目中各参与方有可能面对的潜在风险，估算不同参与方式下的综合成本，通过比较各参与方对成本的节约来确定其对项目的贡献程度，在此基础上运用Shapley模型计算各方应获取的收益，进而确定公私合营模式的股权结构。文章在所构建的理论模型基础上，运用某港口集团的T项目进行案例分析，最后得出以下三点结论:

1.公私合营项目的成本计算中应考虑风险因素。不同参与方对政治、法律、建设、运营等风险的控制能力不同，风险分配也应不同;

2.公私合营项目可以看作合作博弈，并且可以形成稳定的合作联盟;3.博弈理论中的Shapley值法在解决公私合营项目股权结构问题上是可行的。

[1]Al-Sobiei O S.Assessment of risk allocation in construction projects[D].Chicago:Illinois Institute of Technology，2001.

[2]刘新平，王守清.试论PPP项目的风险分配原则和框架[J].建筑经济，2006(2):59-63.

[3]杨秋波，侯晓文.PPP模式风险分担框架的改进研究[J].项目管理技术，2008，6(8):13-17.

[4]Jin Xiaohua，Zhang Guomin.Modelling optimal risk allocation in PPP projects using artificial neural networks[J].International Journal of Project Management，2011(7):591-603.

[5]Tiong R L K.Risks and guarantees in BOT tender[J].Journal of Construction Engineering and Management，1995，121(2):183-188.

[6]Michel J.Risk-allocation:Theoretical and empirical evidences，application to public-private partnerships in the defense sector[C].The 9th Annual Conference of the Institutions of Market，Barcelona，Spain，2005.

[7]孙慧，范志清，石烨.PPP模式下高速公路项目最优股权结构研究[J].管理工程学报，2011(1):154-157.

[8]叶晓甦，易朋成，吴书霞.PPP项目控制权本质探讨[J].科技进步与对策，2011(7):67-70.

[9]刘宇文，王守清.PPP项目再融资最优资本结构研究[D].清华大学，2012.

[10]Dias Jr.A，Ioannou P G.Debt capacity and optimal capital structure for privately financed infrastructure projects[J].Journal of Construction Management and Engineering，1995，121(4):404-414.

[11]范如国.博弈论[M].武汉:武汉大学出版社，2011.

[12]邓小鹏，华建革，李启明，李先光.PPP项目风险分担方式研究[J].建筑经济，2008(12):62-66.